Fünfeck

Regelmäßiges Fünfeck

Ein Fünfeck, auch Pentagon (von altgriechisch πεντάγωνον pentágōnon „Fünfeck“), ist eine geometrische Figur. Es gehört zur Gruppe der Vielecke (Polygone) und ist durch fünf Punkte definiert.

Einteilung

Fünfecke können, wie alle Polygone, welche keine Dreiecke sind, unterteilt werden in:

überschlagenes Fünfeck: Mindestens zwei Seiten schneiden einander.
konkaves Fünfeck: mindestens ein Innenwinkel ist größer als 180°. Ein Fünfeck kann maximal zwei derartige Winkel haben.
konvexes Fünfeck: alle Innenwinkel sind kleiner als 180°
Sehnenfünfeck: alle Ecken liegen auf einem gemeinsamen Umkreis.
regelmäßiges Fünfeck: Alle Seiten sind gleich lang und alle Innenwinkel gleich groß. Regelmäßige Fünfecke können konvex oder überschlagen sein.

Regelmäßiges Fünfeck

Winkel

Die Summe der Innenwinkel eines regelmäßigen Fünfecks beträgt 540°, also 3 mal 180°, und ergibt sich aus einer allgemeinen Formel für Polygone, in der für die Variable die Anzahl der Eckpunkte des Polygons eingesetzt werden muss (in diesem Fall n = 5 ):

$\sum {\alpha =}(n - 2) \cdot 180^\circ = 3 \cdot 180^\circ = 540^\circ$

Fläche

Ein ebenes Fünfeck besitzt einen eindeutig bestimmbaren Flächeninhalt, welcher sich stets durch Zerlegen in Dreiecke berechnen lässt.

Regelmäßiges Fünfeck

Formeln

Mathematische Formeln zum regelmäßigen Fünfeck
Flächeninhalt	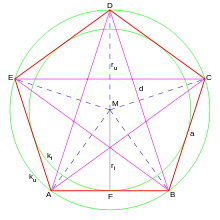$A={\frac {a^{2}}{4}}\cdot {\sqrt {25+10\cdot {\sqrt {5}}}}\approx 1{,}720\cdot a^{2}$
Höhe	$h=r_{u}+r_{i}={\frac {a}{2}}\cdot {\sqrt {5+2\cdot {\sqrt {5}}}}\approx 1{,}539\cdot a$
Länge der Diagonalen	$d={\frac {a}{2}}\cdot (1+{\sqrt {5}})\approx 1{,}618\cdot a$
Inkreisradius	$r_{i}={\frac {a}{10}}\cdot {\sqrt {25+10\cdot {\sqrt {5}}}}\approx 0{,}688\cdot a$
Umkreisradius	$r_{u}={\frac {a}{10}}\cdot {\sqrt {50+10\cdot {\sqrt {5}}}}\approx 0{,}851\cdot a$
Innenwinkel	$\alpha = 108^\circ$

Anschauungshilfe zur Herleitung nebenstehender Aussagen über Winkel

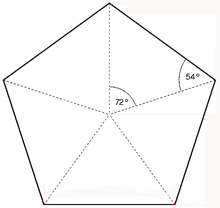
Innenwinkel

Der Winkel, den zwei benachbarte Seiten im ebenen, regelmäßigen Fünfeck miteinander einschließen, beträgt (wiederum nach einer allgemeinen Formel für regelmäßige Polygone):

$\alpha =\frac{(n - 2)}{n} \cdot 180^\circ = \frac{3}{5} \cdot 180^\circ = 108^\circ$

Fläche

Die Fläche A eines regelmäßigen Fünfecks der Seitenlänge ist das Fünffache der Fläche eines von seinem Mittelpunkt und zwei seiner Eckpunkte aufgespannten Dreiecks.

$A=5\cdot {\frac {1}{2}}\cdot a\cdot \tan 54^{\circ }\cdot {\frac {a}{2}}={\frac {5}{4}}\cdot a^{2}\cdot \tan 54^{\circ }\approx 1{,}720\cdot a^{2}$

Allgemein mit dem Umkreisradius r_u

$A={\frac {5}{8}}\cdot r_{u}^{2}\cdot {\sqrt {10+2\cdot {\sqrt {5}}}}$

oder auch

$A={\frac {5}{2}}\cdot r_{u}^{2}\cdot \sin {72^{\circ }}\approx 2{,}378\cdot r_{u}^{2}$

Seitenlänge

$a=2\cdot r_{u}\cdot \sin 36^{\circ }$

oder auch:

$a=r_{u}\cdot {\sqrt {\frac {5-{\sqrt {5}}}{2}}}\approx 1{,}176\cdot r_{u}$

zur Umrechnung siehe den Abschnitt über die als Quadratwurzeln angebbaren Sinus- und Cosinus-Werte.

Der Goldene Schnitt im Fünfeck

Pentagramm

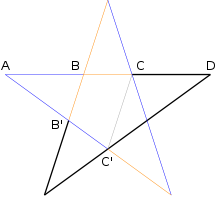
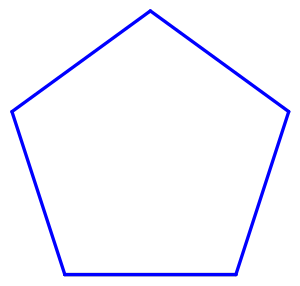
Regelmäßiges Fünfeck und Pentagramm bilden eine Grundfigur, in der das Verhältnis des Goldenen Schnittes wiederholt auftritt. Die Seite des Fünfecks befindet sich im goldenen Verhältnis zu seinen Diagonalen. Die Diagonalen untereinander teilen sich wiederum im goldenen Verhältnis, d.h. AD verhält sich zu BD wie BD zu CD.

Der Beweis nutzt die Ähnlichkeit gewählter Dreiecke.

Jede Seite des Fünfecks befindet sich im goldenen Verhältnis zu jeder seiner beiden benachbarten Diagonalen.

Die Diagonalen teilen sich untereinander im goldenen Verhältnis.

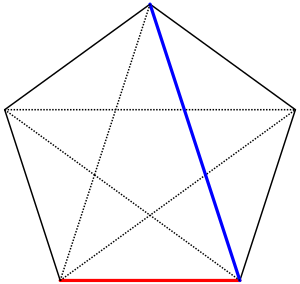
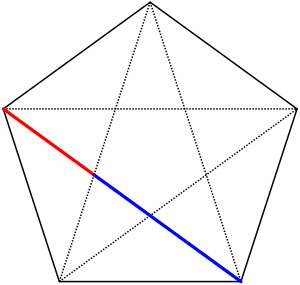
Konstruktion mit Zirkel und Lineal bei gegebenem Umkreis

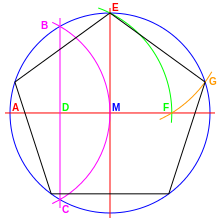
Konstruktion eines Fünfecks in einem umschließenden Kreis

Für das regelmäßige Fünfeck existiert eine mathematisch exakte Konstruktion zur Bestimmung der Seitenlänge (siehe Abbildung).

Zeichne einen Kreis (späterer Umkreis, blau) mit Radius r um den Mittelpunkt M.
Zeichne zwei zueinander senkrechte Durchmesser (rot) ein.
Halbiere einen Radius (magenta, Punkt D).
Zeichne einen Kreis (grün) mit dem Radius DE um Punkt D. Er schneidet die Gerade AM im Punkt F. Die Strecke EF ist die Länge der Seite.
Zum Abtragen auf dem Umkreis einen weiteren Kreisbogen (orange) mit Radius EF um E zeichnen. Er schneidet den ersten Kreis (blau) in G. Vorgang entsprechend wiederholen.

Berechnung zur Konstruktion:

$\overline{EM}= r \cdot 1$

$\overline{DM}= r \cdot \frac{1}{2}$

$\overline {DE}=r\cdot {\sqrt {1+\left({\frac {1}{2}}\right)^{2}}}=r\cdot {\frac {{\sqrt {5}}}{2}}$

${\overline {MF}}=r\cdot \left({\frac {\sqrt {5}}{2}}-{\frac {1}{2}}\right)=r\cdot {\frac {{\sqrt {5}}-1}{2}}$

$\overline {EF}=r\cdot {\sqrt {1+\left({\frac {{\sqrt {5}}-1}{2}}\right)^{2}}}$

Umformen des Faktors:

${\frac {\overline {EF}}{r}}={\sqrt {1+{\frac {5-2\cdot {\sqrt {5}}+1}{4}}}}={\sqrt {{\frac {4}{4}}+{\frac {5-2\cdot {\sqrt {5}}+1}{4}}}}$

$\frac{\overline{EF}}{r} = \sqrt{\frac{4+5- 2 \cdot \sqrt{5} +1}{4}} = \sqrt{\frac{10- 2 \cdot \sqrt{5}}{4}}$

$\frac{\overline{EF}}{r} = \sqrt{ \frac{5 - \sqrt{5}}{2}}$

Das entspricht genau dem Faktor in der obigen Formel für die Seitenlänge.

Die Seiten des nicht eingezeichneten Dreiecks MFE entsprechen exakt den Seitenlängen des regelmäßigen Sechsecks (ME), des regelmäßigen Fünfecks (EF) und des regelmäßigen Zehnecks (FM) mit dem gegebenen Umkreisradius r.

Konstruktion mit Zirkel und Lineal bei gegebener Seite

Mit Anwendung des Goldenen Schnitts, äußere Teilung

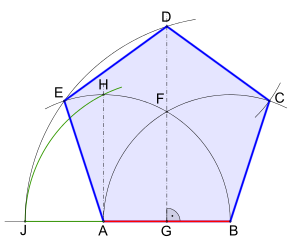
Fünfeck bei gegebener Seitenlänge

Zeichne eine Strecke AB, welche die Länge der vorgegebenen Seite des Fünfecks hat.
Verlängere die Strecke ab dem Punkt A um ca. drei Viertel der Strecke AB.
Zeichne einen Kreisbogen um den Punkt B mit dem Radius AB.
Zeichne einen Kreisbogen um den Punkt A mit dem Radius AB, es ergibt sich der Schnittpunkt F.
Fälle ein Lot von Punkt F auf die Strecke AB mit Fußpunkt G.
Zeichne eine Parallele zur Strecke FG ab dem Punkt A bis über den Kreisbogen um Punkt A, es ergibt sich der Schnittpunkt H.
Zeichne einen Kreisbogen um den Punkt G mit dem Radius GH bis zur Verlängerung der Strecke AB, es ergibt sich der Schnittpunkt J.
Zeichne einen Kreisbogen um den Punkt B mit dem Radius BJ bis über die Senkrechte, die durch den Punkt F geht, es ergeben sich die Schnittpunkte D auf der Senkrechten und E mit dem Kreisbogen um Punkt A.
Zeichne einen Kreisbogen um den Punkt D mit dem Radius BA, bis er den Kreisbogen um Punkt B schneidet, es ergibt sich der Schnittpunkt C.
Verbinde die Punkte B-C-D-E-A, somit ergibt sich das regelmäßige Fünfeck.

Fazit

Wie in der Konstruktion bei gegebenem Umkreis, ist auch hier der Goldene Schnitt der maßgebende Baustein.

Für den Vergleich der Konstruktionsvarianten sind die Punktebezeichnungen mit Indizes ergänzt: u für die Konstruktion mit gegebenem Umkreis, s für die Konstruktion mit gegebener Seitenlänge.

Seite des Fünfecks:
$\overline {E_{u}F_{u}}\;\widehat {=}\;\overline {A_{s}B_{s}}$
Radius für den Goldenen Schnitt:
$\overline {D_{u}E_{u}}\;\widehat {=}\;\overline {G_{s}H_{s}}$
Streckenverhältnisse des Goldenen Schnitts:
$\Phi ={\frac {\overline {A_{u}F_{u}}}{\overline {A_{u}M_{u}}}}={\frac {\overline {A_{u}M_{u}}}{\overline {M_{u}F_{u}}}}\;\;\;=\;\;\;{\frac {\overline {B_{s}J_{s}}}{\overline {A_{s}B_{s}}}}={\frac {\overline {A_{s}B_{s}}}{\overline {A_{s}J_{s}}}}\;\;\;=\;\;\;{\frac {1+{\sqrt {5}}}{2}}\approx 1{,}618$

Polyeder mit regelmäßigen Fünfecken

Das Dodekaeder ist der einzige platonischen Körper, der regelmäßige Fünfecke als Seitenflächen hat. Auch einige archimedische Körper enthalten regelmäßige Fünfecke, nämlich das Ikosidodekaeder, der Ikosaederstumpf, das Rhombenikosidodekaeder und das abgeschrägte Dodekaeder.

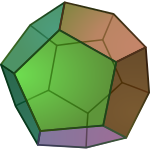Dodekaeder
Ikosidodekaeder
Ikosaederstumpf (Fußballkörper)
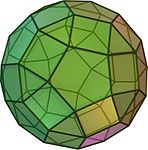Rhombenikosidodekaeder
Abgeschrägtes Dodekaeder

Papierfaltung

Durch Zusammenziehen eines aus einem Papierstreifen geschlungenen Überhandknotens nimmt dieser die Form eines regulären Fünfecks an.

Verknoteter Papierstreifen

Parkettierung mit Fünfecken

Die 15 Typen der ebenen Parkettierung mit kongruenten, konvexen Fünfecken

Es gibt nur 15 verschiedene Fünfecke, mit denen sich eine Fläche lückenlos kacheln lässt, wenn nur eine Form von Kacheln benutzt wird. Den Beweis dafür lieferte der französische Mathematiker Michaël Rao erst 2017.

Vorkommen

Natur

Okrafrüchte

Die Okra-Frucht hat im Querschnitt die Form eines Fünfecks. Die Blüten der Prunkwinde sind ebenfalls fünfeckig ausgebildet. Viele cyclische Verbindungen enthalten eine Fünfringstruktur (etwa Cyclopentan γ-Butyrolacton, Furan, Furanosen etc.).

Architektur und Festungsbau

Zitadelle von Lille
Villa Farnese, Grundriss
Schloss Krzyżtopór
Satellitenaufnahme des Pentagon

Der Grundriss einer neuzeitlichen Festung hat häufig die Form eines Fünfecks. Anschauliche Beispiele für regelmäßige Fünfecke sind oder waren u.a. die vollständig wieder aufgebaute Festung Bourtange in den Niederlanden sowie Nyenschantz (heute in St. Petersburg), die Zitadelle von Pamplona, die Festung Dömitz, die Zitadelle von Turin, die Zitadelle von Amiens, die Zitadelle von Lille, die Zitadelle Vechta, die Zitadelle von Münster, das Kastell von Kopenhagen. Den Typ des befestigten Palasts (Palazzo in fortezza) auf regelmäßig fünfeckigem Grundriss verkörpern die Villa Farnese, die Schlösser Krzyżtopór und Nowy Wiśnicz sowie die Befestigungen von Schloss Łańcut in Polen.

Ein Fünfeck liegt auch der Anlage der Wallfahrtskirche Zelená Hora (Tschechische Republik) und der St. Michael (Detmold-Hiddesen) zugrunde.

Siehe auch

Basierend auf einem Artikel in:

Wikipedia.de