Hyperbolischer Raum

In der Geometrie ist der hyperbolische Raum ein Raum mit konstanter negativer Krümmung. Er erfüllt die Axiome der euklidischen Geometrie mit Ausnahme des Parallelenaxioms. Der zweidimensionale hyperbolische Raum mit konstanter Krümmung heißt hyperbolische Ebene.

Definition

Sei eine natürliche Zahl. Der n-dimensionale hyperbolische Raum $\mathbb H^n$ ist die n-dimensionale, einfach zusammenhängende, vollständige Riemannsche Mannigfaltigkeit mit Schnittkrümmung konstant .

Die Existenz des n-dimensionalen hyperbolischen Raumes ergibt sich aus den unten angegebenen Modellen, die Eindeutigkeit aus dem Satz von Cartan.

Gelegentlich wird die Bezeichnung hyperbolischer Raum auch allgemeiner für $\delta$ -hyperbolische Räume im Sinne von Gromov verwendet. Dieser Artikel betrachtet jedoch im Folgenden nur den hyperbolischen Raum mit Schnittkrümmung −1. Am Ende des Artikels werden weitere (teilweise nicht kompatible) in der Mathematik vorkommende Verwendungen des Begriffes "Hyperbolischer Raum" aufgelistet.

Eindeutigkeit

Aus einem Satz von Elie Cartan folgt, dass der n-dimensionale hyperbolische Raum bis auf Isometrie eindeutig ist. Insbesondere sind die unten angegebenen Modelle des n-dimensionalen hyperbolischen Raumes alle isometrisch zueinander.

Eigenschaften

Hyperbolisches Dreieck

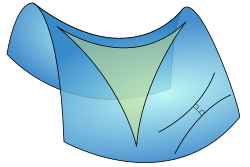
Zu jeder Geodäte und jedem Punkt $P\not\in L$ gibt es unendlich viele zu disjunkte Geodäten durch .

Die Innenwinkelsumme von Dreiecken ist stets kleiner als $\pi$ . Der Flächeninhalt eines Dreiecks ist $\pi - (\alpha+\beta+\gamma)$ , wobei $\alpha,\beta,\gamma$ die Innenwinkel sind.

Trigonometrie

Es gelten die Formeln der hyperbolischen Trigonometrie:

$\frac{\sin \alpha}{\sinh a} = \frac{\sin \beta}{\sinh b} = \frac{\sin \gamma}{\sinh c}$

und

$\cosh c=\cosh a\cosh b-\sinh a\sinh b \cos \gamma,\,$

wobei $\alpha,\beta,\gamma$ die Innenwinkel eines Dreiecks und a,b,c die Längen der gegenüberliegenden Seiten sind.

Exponentielles Wachstum

Das Volumen eines Balles vom Radius ist

${\frac {2\pi ^{n/2}}{\Gamma \left({\frac {n}{2}}\right)}}\int _{0}^{r}\sinh ^{n-1}(\rho )\,d\rho$ ,

es wächst somit exponentiell mit dem Radius.

Isometrien

Geodätische Halbgeraden in $\mathbb H^n$ heißen asymptotisch, wenn sie endlichen Abstand haben. Dies definiert eine Äquivalenzrelation auf der Menge der geodätischen Halbgeraden. Der Rand im Unendlichen $\partial_\infty \mathbb H^n$ ist die Menge der Äquivalenzklassen von auf Bogenlänge parametrisierten geodätischen Halbgeraden. Jede Isometrie $f\colon \mathbb {H} ^{n}\rightarrow \mathbb {H} ^{n}$ lässt sich auf den Rand im Unendlichen $\partial_\infty H^n$ fortsetzen.

Die Isometrien des hyperbolischen Raumes fallen in die folgenden (bis auf die Identitäts-Abbildung disjunkten) Klassen:

elliptisch: hat einen Fixpunkt in $\mathbb H^n$ ,
loxodromisch hat keinen Fixpunkt in $\mathbb H^n$ , lässt aber zwei Punkte in $\partial_\infty\mathbb H^n$ und die sie verbindende Geodäte invariant,
parabolisch: lässt einen Punkt $p\in\partial_\infty \mathbb H^n$ und seine Horosphären invariant.

Die Gruppe der Isometrien des $\mathbb H^n$ ist isomorph zu O^+(n,1) .

Modelle

Poincaré-Halbraum-Modell

Teilung der oberen Halbebene in isometrische geodätische Siebenecke

Der Halbraum

$\left\{(x_1,\ldots,x_n)\in\mathbb R^n: x_n>0\right\}\subset \mathbb R^n$

mit der Riemannschen Metrik

$\frac{(dx_1)^2+\ldots+(dx_n)^2}{x_n^2}$

ist ein Modell des hyperbolischen Raumes.

Für n=2 wird es auch als Poincaré-Halbebenen-Modell bezeichnet.

Poincaré-Ball-Modell

Teilung der Kreisscheibe: Gleichfarbige Gebiete sind isometrisch zueinander im Poincaré-Ball-Modell.

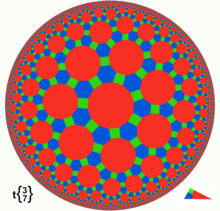
Die offene Kugel

$\left\{(x_1,\ldots,x_n)\in\mathbb R^n: x_1^2+\ldots+x_n^2<1\right\}\subset \mathbb R^n$

mit der Riemannschen Metrik

$4\frac{(dx_1)^2+\ldots+(dx_n)^2}{\left(1-x_1^2-\ldots-x_n^2\right)^2}$

ist ein Modell des hyperbolischen Raumes.

Für n=2 wird es auch als Poincaré-Kreisscheiben-Modell bezeichnet.

Hyperboloid-Modell

Betrachte den $\mathbb R^{n+1}$ mit der Pseudo-Riemannschen Metrik $-(dx_{1})^{2}+(dx_{2})^{2}+\ldots +(dx_{n+1})^{2}$ .

Das Hyperboloid

$\left\{(x_{1},\ldots ,x_{n+1})\in \mathbb {R} ^{n+1}:-x_{1}^{2}+x_{2}^{2}\ldots +x_{n+1}^{2}=1,x_{1}>0\right\}\subset \mathbb {R} ^{n+1}$

mit der induzierten Metrik ist ein Modell des hyperbolischen Raumes.

Projektives Modell

Teilung der Kreisscheibe in Drei- und Siebenecken, die im Beltrami-Klein-Modell geodätisch und jeweils isometrisch zueinander sind.

Sei $p\colon \mathbb {R} ^{n+1}\setminus \{0\}\rightarrow \mathbb {R} P^{n}$ die kanonische Projektion auf den projektiven Raum, dann erhält man das projektive Modell des hyperbolischen Raumes als Bild des Hyperboloids unter .

Nach der Identifikation $\mathbb RP^n=\mathbb R^n\cup\mathbb RP^{n-1}$ entspricht das projektive Modell der Menge

$\left\{(x_1,\ldots,x_n)\in\mathbb R^n: x_1^2+\ldots+x_n^2<1\right\}\subset \mathbb R^n$ .

Abstände berechnen sich gemäß der Hilbert-Metrik

$d(p,q)=\frac{1}{2} \log \frac{|qa||bp|}{|pa||bq|}$ ,

wobei die Betragsstriche für euklidische Abstände stehen sollen und a,b die Schnittpunkte der Geodäten durch p,q mit der Einheitssphäre sind.

Historie

Das Projektive Modell, das Poincaré-Ball-Modell und das Poincaré-Halbraum-Modell wurden 1868 von Eugenio Beltrami konstruiert, alle drei als Bilder eines weiteren (sogenannten "hemisphärischen") Modells unter geeigneten Isometrien. Das Poincaré-Ball-Modell war für n=2 bereits 1850 von Joseph Liouville untersucht worden und das projektive Modell kam 1859 in einer Arbeit Arthur Cayleys zur projektiven Geometrie vor, allerdings ohne Herstellung des Zusammenhangs zur hyperbolischen Geometrie.

Zuvor hatten Nikolai Iwanowitsch Lobatschewski und János Bolyai eine auf Axiomen aufbauende Theorie des hyperbolischen Raumes entwickelt und zahlreiche seiner Eigenschaften formal hergeleitet. Erst mit den von Beltrami angegebenen Modellen war aber der Beweis erbracht, dass die hyperbolische Geometrie widerspruchsfrei ist.

Henri Poincaré entdeckte, dass die hyperbolische Geometrie auf natürliche Weise bei der Untersuchung von Differentialgleichungen und in der Zahlentheorie (bei der Untersuchung von quadratischen Formen) vorkommt. Im Zusammenhang mit der Untersuchung ternärer quadratischer Formen benutzte er 1881 erstmals das Hyperboloid-Modell.

Homogener Raum

Der hyperbolische Raum ist der homogene Raum

$\mathbb {H} ^{n}=O(n,1)/(O(n)\times O(1))=O_{0}(n,1)/O(n)=SO_{0}(n,1)/SO(n),$

wobei $(S)O_{0}(n,1)$ die Zusammenhangskomponente der Eins in $(S)O(n,1)$ bezeichnet.

Damit ist hyperbolische Geometrie eine Geometrie im Sinne von Felix Kleins Erlanger Programm.

Für n=2,3 hat man auch die Darstellungen

$\mathbb {H} ^{2}=SL(2,\mathbb {R} )/SO(2)$

$\mathbb {H} ^{3}=SL(2,\mathbb {C} )/SU(2)$ .

Einbettung in den euklidischen Raum

Der hyperbolische Raum $\mathbb H^n$ besitzt eine isometrische $C^{\infty }$ -Einbettung in den euklidischen Raum $\mathbb R^{4n-3}$ .

Andere Verwendungen des Begriffs „hyperbolischer Raum“

In der metrischen Geometrie sind $\delta$ -hyperbolische Räume im Sinne von Gromov (auch als Gromov-hyperbolische Räume bezeichnet) eine Klasse von metrischen Räumen, zu der unter anderem einfach zusammenhängende Mannigfaltigkeiten negativer Schnittkrümmung (insbesondere also auch der hyperbolische Raum) gehören. Endlich erzeugte Gruppen werden als hyperbolische Gruppen bezeichnet, wenn ihr Cayley-Graph ein $\delta$ -hyperbolischer Raum ist.
In der Theorie der symmetrischen Räume gibt es neben den in diesem Artikel betrachteten hyperbolischen Räumen, die in diesem Zusammenhang oft als reell-hyperbolische Räume bezeichnet werden, noch die komplex-hyperbolischen und quaternionisch-hyperbolischen Räume sowie die Cayley-hyperbolische Ebene. Diese werden für $\mathbb K=\mathbb R, \mathbb C, \mathbb H$ oder $\mathbb O$ definiert als $\left\{(x_1,\ldots,x_{n+1})\in\mathbb K^{n+1}: x_1^2-x_2^2\ldots-x_{n+1}^2=1\right\}\subset \mathbb K^{n+1}$ mit der induzierten Riemannschen Metrik.
In der Inzidenzgeometrie ist ein hyperbolischer Raum ein angeordneter Inzidenzraum mit einer Kongruenzrelation und der Eigenschaft, dass jede Ebene mit der induzierten Anordnung und Kongruenzrelation eine hyperbolische Ebene im Sinne von Karzel-Sörensen-Windelberg ist. Insbesondere gibt es in der endlichen Geometrie den Begriff endlicher hyperbolischer Räume.
In der komplexen Analysis heißt eine komplexe Mannigfaltigkeit Brody-hyperbolisch, wenn jede holomorphe Abbildung $f\colon \mathbb {C} \rightarrow X$ konstant ist. Dies gilt insbesondere für die durch das Poincaré-Kreisscheiben-Modell gegebene komplexe Struktur auf der hyperbolischen Ebene, siehe Satz von Liouville.
Ebenfalls in der komplexen Analysis heißt eine komplexe Mannigfaltigkeit Kobayashi-hyperbolisch (oder nur hyperbolisch), wenn die Kobayashi-Pseudo-Metrik eine Metrik ist. Für kompakte komplexe Mannigfaltigkeiten sind Brody-Hyperbolizität und Kobayashi-Hyperbolizität äquivalent.
In der komplexen Differentialgeometrie heißen Kähler-Mannigfaltigkeiten $(M,\omega)$ Kähler-hyperbolisch, wenn die hochgehobene Kählerform $\widetilde{\omega}$ der universellen Überlagerung $\widetilde{M}$ das Differential einer beschränkten Differentialform ist.
In der Homotopietheorie ist ein hyperbolischer Raum ein topologischer Raum mit $\sum_i rk(\pi_iX)=\infty$ . Hier bezeichnet $\pi_iX$ die i-te Homotopiegruppe und ihren Rang. Diese Definition steht in keinem Zusammenhang mit der in diesem Artikel besprochenen.

Literatur

Eugenio Beltrami: Saggio di interpretazione della geometria non-euclidea. Giornale Matemat. 6 (1868), 284–312
Eugenio Beltrami: Teoria fondamentale degli spazii di curvatura constante. Ann. Mat. Ser. II 2 (1868–69), 232–255
Felix Klein: Über die sogenannte nicht-euklidische Geometrie Math. Ann. 4 (1871), 573–625.

Basierend auf einem Artikel in:

Wikipedia.de