Gruppe vom Lie-Typ

Gruppen vom Lie-Typ sind im mathematischen Teilgebiet der Gruppentheorie untersuchte Gruppen, die sich von gewissen Lie-Algebren herleiten, genauer handelt es sich um Gruppen von Automorphismen von Lie-Algebren. Mit den endlichen unter diesen erhält man 16 unendliche Serien endlicher einfacher Gruppen, die zusammen mit den zyklischen Gruppen von Primzahl-Ordnung und den alternierenden Gruppen die 18 Serien aus dem Klassifikationssatz endlicher einfacher Gruppen bilden.

Tabellarische Übersicht

Wir beginnen mit einer tabellarischen Übersicht, die aus dem Lehrbuch „Finite group Theory“ von Michael Aschbacher adaptiert ist.

Name

Alternative Bezeichnung

Gruppenordnung

Ausnahmen

Isomorphien

$A_{n}(q)$

Spezielle projektive lineare Gruppe

${\frac {q^{n(n+1)/2}}{(n+1,q-1)}}\prod _{i=1}^{n}(q^{i+1}-1)$

$A_{1}(2),A_{1}(3)$

$A_{1}(4)\cong A_{1}(5)\cong A_{5}$

$A_{1}(7)\cong A_{2}(2)$

$A_{1}(9)\cong A_{6}$

$A_{3}(2)\cong A_{8}$

$B_{n}(q),n>1$

Kommutatorgruppe der speziellen orthogonalen Gruppe (ungerader Grad)

${\frac {q^{n^{2}}}{(2,q-1)}}\prod _{i=1}^{n}(q^{2i}-1)$

$B_{n}(2^{m})\cong C_{n}(2^{m})$

$B_{2}(3)\cong {}^{2}\!A_{3}(2^{2})$

$C_{n}(q),n>2$

Projektive symplektische Gruppe

$B_{n}(2^{m})\cong C_{n}(2^{m})$

$D_{n}(q),n>1$

Kommutatorgruppe der speziellen orthogonalen Gruppe (gerader Grad)

${\frac {q^{n(n-1)}(q^{n}-1)}{(4,q^{n}-1)}}\prod _{i=1}^{n}(q^{2i}-1)$

$E_{6}(q)$

Chevalley-Gruppe

${\frac {q^{36}}{(3,q-1)}}\prod _{i=2,5,6,8,9,12}(q^{i}-1)$

$E_{7}(q)$

Chevalley-Gruppe

${\frac {q^{63}}{(2,q-1)}}\prod _{i=2,6,8,10,12,14,18}(q^{i}-1)$

$E_{8}(q)$

Chevalley-Gruppe

$q^{120}\prod _{i=2,8,12,14,18,20,24,30}(q^{i}-1)$

$F_{4}(q)$

Chevalley-Gruppe

$q^{24}\prod _{i=2,6,8,12}(q^{i}-1)$

$G_{2}(q)$

Chevalley-Gruppe

$q^{6}(q^{6}-1)(q^{2}-1)$

$G_{2}(2)$

${}^{2}\!A_{n}(q^{2}),n>1$

Spezielle unitäre Gruppe

${\frac {q^{n(n+1)/2}}{(n+1,q+1)}}\prod _{i=1}^{n}(q^{i+1}-(-1)^{i+1})$

${}^{2}\!A_{2}(2^{2})$

${}^{2}\!A_{3}(2^{2})\cong B_{2}(3)$

${}^{2}\!B_{2}(2^{2m+1})$

Suzuki-Gruppen $\mathrm {Sz} (2^{2m+1})$

$q^{2}(q^{2}-1)(q-1)$ mit $q=2^{2m+1}$

${}^{2}\!B_{2}(2)$

${}^{2}\!D_{n}(q^{2}),n>3$

Steinberg-Gruppe

${\frac {q^{n(n-1)}(q^{n}+1)}{(4,q^{n}+1)}}\prod _{i=1}^{n-1}(q^{2i}-1)$

${}^{3}\!D_{4}(q^{3})$

Steinberg-Gruppe

$q^{12}(q^{8}+q^{4}+1)(q^{6}-1)(q^{2}-1)$

${}^{2}\!E_{6}(q^{2})$

Steinberg-Gruppe

${\frac {q^{36}(q^{n}+1)}{(3,q+1)}}\prod _{i=2,5,6,8,9,12}(q^{i}-(-1)^{i}$

${}^{2}\!F_{4}(2^{2m+1})$

Ree-Gruppe

$q^{12}(q^{6}+1)(q^{4}-1)(q^{3}+1)(q-1)$ mit $q=2^{2m+1}$

${}^{2}\!F_{4}(2)$

${}^{2}\!G_{2}(3^{2m+1})$

Ree-Gruppe

$q^{3}(q^{3}+1)(q-1)$ mit $q=2^{3m+1}$

${}^{2}\!G_{2}(3)$

Die Namen ergeben sich aus den Typen von Lie-Algebren, wie unten erläutert wird. In obiger Tabelle ist stets eine Primzahlpotenz und eine natürliche Zahl inklusive 0, die in den Nennern der Formeln für die Gruppenordnung vorkommenden Klammern $(\cdot ,\cdot )$ stehen für den größten gemeinsamen Teiler. Viele dieser Gruppen waren bereits vor Chevalleys Arbeiten als sogenannte klassische Gruppen bekannt, manche sind auch nach ihren Entdeckern benannt. Die daher rührenden Bezeichnungen sind als "Alternative Bezeichnung" angegeben. Die genannten Ausnahmen sind nicht-einfache Gruppen, ferner bestehen die in der Spalte "Isomorphie" genannten Isomorphien unter diesen Gruppen und zu den alternierenden Gruppen A_n (ist mit $A_{n}$ der Lie-Typ gemeint, so folgt stets eine in Klammern gesetzte Primzahlpotenz).

Im Folgenden werden die zur Definition dieser Gruppen benötigten Begriffe entwickelt, wobei wir im Wesentlichen dem unten angegebenen Lehrbuch "Simple Groups of Lie-Type" von Roger Carter folgen, das ganz diesem Thema gewidmet ist, auch wenn dieses Buch bereits älter ist und aus der Zeit vor dem Klassifikationssatz stammt. Ausgehend von der Klassifikation einfacher Lie-Algebren über $\mathbb {C}$ beschreiben wir die durchaus verwickelte Konstruktion dieser Gruppen und führen dabei gerade soviel Begriffe ein, wie für die Definition der Gruppen erforderlich ist.

Die Darstellung zerfällt in zwei große Blöcke. Zunächst konstruieren wir die sogenannten klassischen Chevalley-Gruppen, deren Theorie auf Claude Chevalley zurückgeht; es sind dies die Gruppen ohne einen linken oberen Index in ihrem Namen. Im zweiten Block werden Automorphismen auf gewissen klassischen Chevalley-Gruppen konstruiert, deren Ordnung ist gerade der linke obere Index. Aus gewissen Fixpunktmengen dieser Automorphismen konstruiert man die sogenannten getwisteten Chevalley-Gruppen als Untergruppen der klassischen Chevalley-Gruppen. Diese wurden unabhängig von Robert Steinberg, Jacques Tits und Ravi Hertzig entdeckt.

Einfache Lie-Algebren

Wurzelsysteme

Es sei $(L,[\cdot ,\cdot ])$ eine einfache, endlichdimensionale Lie-Algebra über $\mathbb {C}$ und $(\cdot ,\cdot )_{L}$ die nicht-ausgeartete Killing-Form. Dann gibt es gemäß der Theorie der Lie-Algebren eine solgenannte Cartan-Zerlegung

$L=H\oplus \bigoplus _{r\in \Phi }L_{r}$ , wobei

eine Cartan-Unteralgebra ist, es gilt sogar $[H,H]=0$ ,
$\Phi \subset H$ ein sogenanntes Wurzelsystem in der $\mathbb {R}$ -linearen Hülle $H_{\mathbb {R} }$ von $\Phi$ ,
$L_{r}=\mathbb {C} e_{r}\subset L$ für jedes $r\in \Phi$ ein eindimensionaler Unterraum, $e_{r}$ ist ein Vektor aus $L_{r}\setminus \{0\}$
$[H,L_{r}]=L_{r}$ für alle $r\in \Phi$ ,
$[h,e_{r}]=(h,r)_{L}\cdot e_{r}$ für alle $r\in \Phi ,h\in H$ .

$H_{\mathbb {R} }$ ist mit der Einschränkung der Killing-Form ein euklidischer Raum, in dem man daher Längen und Winkel zwischen Vektoren messen kann, und die Wurzelsystem-Eigenschaften führen zu starken Restriktionen für die relativen Längen der Vektoren aus $\Phi$ und den Winkeln zwischen ihnen. Wie bei jedem Wurzelsystem kann man eine Teilmenge $\Phi _{0}\subset \Phi$ von sogenannten fundamentalen Wurzeln auswählen, so dass

$\Phi _{0}=\{r_{1},\ldots ,r_{n}\}$ eine Vektorraumbasis von ist
alle Koeffizienten in der Entwicklung eines Vektors $r\in \Phi$ nach der Basis $\Phi_0$ dasselbe Vorzeichen haben
$n_{i,j}:={\frac {4(r_{i},r_{j})_{L}^{2}}{(r_{i},r_{i})_{L}(r_{j},r_{j})_{L}}}\in \{0,1,2,3\}$ für alle $i\not= j$ .

Dynkin-Diagramme

Die Dynkin-Diagramme sind den Wurzelsystemen zugeordnete Graphen.

Aus dem gerade vorgestellten Wurzelsystem konstruiert man das sogenannte Dynkin-Diagramm, das ist der Graph mit der Knotenmenge $\Phi_0$ und $n_{{i,j}}$ Kanten zwischen $r_{i},r_{j}\in \Phi _{0}$ . Die Eigenschaften eines Wurzelsystems sind derart restriktiv, dass es nur folgende in nebenstehender Übersicht wiedergegebene Möglichkeiten, sogenannte Typen, gibt:

$A_{n},n\geq 1,\quad B_{n},n\geq 2,\quad C_{n},n\geq 3,\quad D_{n},n\geq 4,\quad E_{6},E_{7},E_{8},\quad F_{4},\quad G_{2}$ .

Dabei steht ein " < " bzw. " > " über den Kanten zwischen zwei fundamentalen Wurzeln für eine entsprechende Größenrelation der Längen der fundamentalen Wurzeln.

Trotz der vielen Wahlmöglichkeiten in der grob umrissenden Konstruktion stellt dies eine vollständige Klassifikation aller einfachen, endlichdimensionalen $\mathbb {C}$ -Lie-Algebren dar. Zwei einfache, endlichdimensionale $\mathbb {C}$ -Lie-Algebren sind genau dann isomorph, wenn sie dasselbe Dynkin-Diagramm haben, und zu jedem der aufgelisteten Dynkin-Diagramme gibt es eine einfache, endlichdimensionale $\mathbb {C}$ -Lie-Algebra. Diese Klassifikation geht im Wesentlichen auf Élie Cartan und Wilhelm Killing zurück. Oft bezeichnet man eine einfache, endlichdimensionale $\mathbb {C}$ -Lie-Algebra einfach durch ihren Typ.

Chevalley-Gruppen

Chevalley-Basis

Wir gehen von einer einfachen, endlichdimensionalen $\mathbb {C}$ -Lie-Algebra aus und verwenden die oben eingeführten Begriffe. Für zwei Wurzeln $r,s\in \Phi$ sei

$h_{r}:={\frac {2r}{(r,r)_{L}}}$ , dadurch werden die fundamentalen Wurzeln geeignet "normiert".
$A_{r,s}:={\frac {2(r,s)_{L}}{(r,r)_{L}}}$ , diese Zahlen sind stets aus $\mathbb {Z}$ .
$p_{r,s}:=\max\{p\in \mathbb {N} _{0}\mid s-pr\in \Phi \}$ .

Die $h_{r_{i}}$ bilden natürlich ebenfalls eine Basis der Cartan-Unteralgebra , weshalb $\{h_{r}\mid r\in \Phi _{0}\}\cup \{e_{r}\mid r\in \Phi \}$ eine Basis von ist.

Claude Chevalley hat gezeigt, dass man die Wahlen so treffen kann, dass eine heute sogenannte Chevalley-Basis vorliegt, das heißt, dass Folgendes gilt:

$[h_{r},h_{s}]=0$ für alle $r,s\in \Phi$
$[h_{r},e_{s}]=A_{r,s}e_{s}$ für alle $r,s\in \Phi$
$[e_{r},e_{s}]=0$ für alle $r,s\in \Phi$ mit $r+s\notin \Phi$
$[e_{r},e_{s}]=N_{r,s}e_{r+s}$ für alle $r,s\in \Phi$ mit $r+s\in \Phi$ , wobei $N_{r,s}=\pm (p_{r,s}+1)$ .

Bei den Vorzeichen der $N_{r,s}$ bleiben gewisse Wahlmöglichkeiten.

Chevalley-Gruppen über ℂ

Die oben genannten Relationen zwischen den Elementen einer Chevalley-Basis zeigen, dass für jedes $r\in \Phi$ die Derivation

$\mathrm {ad} \,e_{r}:\,L\rightarrow L,\,x\mapsto [e_{r},x]$

ein nilpotentes Element der Algebra der linearen Operatoren auf ist, das heißt $(\mathrm {ad} \,e_{r})^{m}=0$ für ein hinreichend großes $m\in \mathbb{N}$ . Das gilt dann auch für jedes skalare Vielfache $\zeta \cdot \mathrm {ad} \,e_{r}$ , das heißt für jedes $\zeta \in \mathbb {C}$ ist

$x_{r}(\zeta ):=\exp(\zeta \cdot \mathrm {ad} \,e_{r})=\mathrm {id} _{L}+\sum _{k\geq 1}{\frac {1}{k!}}\zeta ^{k}(\mathrm {ad} \,e_{r})^{k}$

eine endliche Summe. Daher funktioniert der übliche Beweis, wonach die Exponentialfunktion einer Derivation ein Automorphismus ist. Die von den Automorphismen $x_{r}(\zeta ),\,r\in \Phi ,\zeta \in \mathbb {C}$ erzeugte Gruppe heißt Chevalley-Gruppe und wird mit $L(\mathbb {C} )$ bezeichnet. Dabei kann die Lie-Algebra auch durch ihren Typ ersetzt werden, das heißt man schreibt $A_{n}(\mathbb {C} ),B_{n}(\mathbb {C} ),\ldots$ . Die Operation von $x_{r}(\zeta )$ auf den Elementen einer Chevalley-Basis erhält man ebenfalls aus den oben genannten Relationen:

$x_{r}(\zeta )h_{r}=h_{r}-2\zeta e_{r}$
$x_{r}(\zeta )e_{r}=e_{r}$
$x_{r}(\zeta )e_{-r}=e_{-r}+\zeta h_{r}-\zeta ^{2}e_{r}$
$x_{r}(\zeta )h_{s}=h_{s}-A_{s,r}\zeta e_{r}$ für von r linear unabhängige $s\in \Phi$
$x_{r}(\zeta )e_{s}=\sum _{i=0}^{k}M_{r,s,i}\zeta ^{i}e_{ir+s}$ ,

wobei dadurch bestimmt ist, dass alle $ir+s$ zu $\Phi$ gehören für $0\leq i\leq k$ und

$M_{r,s,i}:={\frac {1}{i!}}\prod _{j=0}^{i-1}N_{r,jr+s}=\pm {\frac {(p_{r,s}+1)\cdots (p_{r,s}+i)}{i!}}=\pm {\binom {p+i}{i}}\in \mathbb {Z}$

Chevalley-Gruppen über K

Eine weitere einfache Folgerung aus obigen Relationen zwischen den Elementen einer Chevalley-Basis ist, dass die $\mathbb {Z}$ -lineare Hülle $\mathbb {Z} \Phi$ bzgl. der Lie-Klammer abgeschlossen ist und daher einen Lie-Ring bildet, das heißt $\mathbb {Z} \Phi$ erfüllt alle Axiome einer Lie-Algebra bis auf diejenigen, die die skalare Multiplikation betreffen. Ist nun ein beliebiger Körper, so kann man das Tensorprodukt $K\otimes _{\mathbb {Z} }\mathbb {Z} \Phi$ bilden, denn jeder Körper ist in natürlicher Weise ein ℤ-Modul. Jedes Element von $K\otimes _{\mathbb {Z} }\mathbb {Z} \Phi$ hat die Form

$\sum _{r\in \Phi _{0}}t_{r}(1_{K}\otimes h_{r})+\sum _{r\in \Phi }s_{r}(1_{K}\otimes e_{r})$ ,

wobei 1_K das Einselement in sei und die $t_{r},s_{r}$ Elemente aus seien. Durch die Festlegung

$[1_{K}\otimes x,1_{K}\otimes y]:=1_{K}\otimes [x,y]$

erhalten wir eine -Lie-Algebra $L_{K}$ . Die Menge $\{1_{K}\otimes h_{r}\mid r\in \Phi _{0}\}\cup \{1_{K}\otimes e_{r}\mid r\in \Phi \}$ ist eine Basis von $L_{K}$ und es gelten nach Definition der Lie-Klammer auf $L_{K}$ dieselben Relationen wie zwischen den Elementen der Chevalley-Basis, wobei jede ganze Zahl , die in den Relationen vorkommt, als $a\cdot 1_{K}\in K$ zu verstehen ist, das heißt jede ganze Zahl wird wie üblich auf ein Element des Primkörpers von abgebildet, das wird im Folgenden nicht mehr erwähnt.

Ganz analog kann man nun wie folgt Operatoren $x_{r}(t)$ auf $L_{K}$ erklären. Jedes $x_{r}(\zeta )$ hat bzgl. der Chevalley-Basis eine Matrix-Darstellung mit Matrixelementen $a\zeta ^{i},\,a\in \mathbb {Z} ,i\in \mathbb {N} _{0}$ , wie man an obigen Formeln für die Operation der $x_{r}(\zeta )$ auf den Basiselementen ablesen kann. Für jedes $t\in K$ definiert dann die Matrix mit den entsprechenden Matrixelementen $at^{i}$ einen mit $x_{r}(t)$ bezeichneten Automorphismus auf $L_{K}$ . Dieser operiert wie folgt auf den Basiselementen:

$x_{r}(t)h_{r}=h_{r}-2te_{r}$
$x_{r}(t)e_{r}=e_{r}$
$x_{r}(t)e_{-r}=e_{-r}+th_{r}-t^{2}e_{r}$
$x_{r}(t)h_{s}=h_{s}-A_{s,r}te_{r}$ für von r linear unabhängige $s\in \Phi$
$x_{r}(t)e_{s}=\sum _{i=0}^{k}M_{r,s,i}t^{i}e_{ir+s}$ mit demselben wie in obigen Formeln für $x_{r}(\zeta )$

Beachte, dass alle Koeffizienten in diesen Gleichungen ganzzahlig sind.

Die von den Automorphismen $x_{r}(t),\,r\in \Phi ,t\in K$ erzeugte Gruppe heißt die Chevalley-Gruppe über und wird mit $L(K)$ bezeichnet.

$L(K):=\langle x_{r}(t)\mid r\in \Phi ,t\in K\rangle$

Die Gruppen $L(K)$ sind bis auf Isomorphie eindeutig durch die Isomorphieklassen der einfachen, endlichdimensionalen $\mathbb {C}$ -Lie-Algebra und des Körpers bestimmt. Ist endlich, so ist bereits durch die Anzahl seiner Elemente, die eine Primzahlpotenz sein muss, bis auf Isomorphie eindeutig bestimmt und man schreibt daher $L(q)$ statt $L(K)$ . Statt genügt die Angabe des Typs, und man schreibt daher $A_{n}(q),B_{n}(q),\ldots$ . Für diese Gruppen gilt folgender Satz:

Ist eine einfache, endlich-dimensionale $\mathbb {C}$ -Lie-Algebra und ein Körper, so ist die Chevalley-Gruppe $L(K)$ einfach bis auf die Ausnahmen $A_{1}(2),A_{1}(3),B_{2}(2),G_{2}(2)$ .

Damit sind die ersten neun Serien einfacher Gruppen obiger tabellarischer Übersicht erklärt.

Getwistete Chevalley-Gruppen

Automorphismen auf Dynkin-Diagrammen

Nicht-triviale Automorphismen auf Dynkin-Diagrammen.

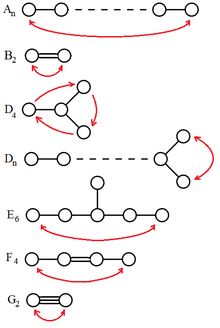
Die getwisteten Chevalley-Gruppen sind Untergruppen der Chevalley-Gruppen, die aus gewissen Fixpunkt-Mengen eines geeigneten Automorphismus $\sigma$ der Chevalley-Gruppe gebildet werden. Ein solcher Automorphismus entsteht aus einem Graphenautomorphismus des Dynkin-Diagramms. Daher verschaffen wir uns zunächst einen Überblick über die möglichen Graphenautomorphismen. Auf den Dynkin-Diagrammen $A_{n}$ hat man für $n\ge 2$ den nicht-trivialen Automorphismus, der den Graphen am horizontalen Zentrum spiegelt, wie in nebenstehender Zeichnung angedeutet.

Auf den Dynkin-Diagrammen $B_{n}$ mit n>2 gibt es keine nicht-trivialen Graphenautomorphismen, denn jeder Graphenautomorphismus muss den einzigen Knoten mit nur einer Kante festlassen und ebenso die Abstände zu diesem Knoten. Für B_2 gilt das natürlich nicht und hier gibt es einen nicht-trivialen Automorphismus, wie in der nebenstehenden Zeichnung angegeben. Dasselbe gilt für $C_{n}$ , $C_{2}$ ist nicht aufgeführt, da dieses mit B_2 zusammenfällt.

Auf $D_{n}$ hat man die Vertauschung der beiden rechten Enden als Graphenautomorphismus. Eine Besonderheit ergibt sich bei $D_{4}$ , hier ist die angegebene Rotation ebenfalls ein nicht-trivialer Graphenautomorphismus.

In den $E_{n}$ -Diagrammen gibt es genau einen Knoten mit drei Kanten, der daher unter jedem Graphenautomorphismus fix bleiben muss. Das bereits oben bei $B_{n}$ gegebene Abstandsargument zeigt, dass $E_{7}$ und E_8 keine nicht-trivialen Graphenautomorphismen haben können, $E_{6}$ hat den in der Zeichnung angedeuteten Graphenautomorphismus. Für F_4 und $G_{2}$ liegt der Graphenautomorphismus auf der Hand.

Man beachte, dass fast alle angegebenen Graphenautomorphismen die Ordnung 2 haben. Die einzige Ausnahme ist das Dynkin-Diagramm $D_{4}$ , auf dem es einen Graphenautomorphismus der Ordnung 2 und einen der Ordnung 3 gibt.

Automorphismen auf den Chevalley-Gruppen

Ist nun $\rho$ ein Graphenautomorphismus auf einem Dynkin-Diagramm, so kann man tatsächlich einen Automorphismus $\sigma$ der zugehörigen Chevalley-Gruppe finden, der $X_{r}:=\{x_{r}(t)|t\in K\}$ für jedes $r\in \Phi _{0}$ auf $X_{\rho (r)}$ abbildet, wobei der Körper im Falle von B_2 und F_4 vollkommen und von der Charakteristik 2 und im Falle von $G_{2}$ vollkommen und von der Charakteristik 3 sein muss.

Damit der Gruppenautomorphismus $\sigma$ dieselbe Ordnung wie der Graphenautomorphismus $\rho$ hat, muss man noch gewisse Körperautomorphismen ins Spiel bringen, was im Falle der uns interessierenden endlichen Körper zu weiteren Einschränkungen führt, die sich insgesamt wie folgt darstellen, wobei stets für eine Primzahlpotenz steht:

Typ $A_{n},D_{n},E_{6}$ : muss ein Quadrat sein, also $|K|=q^{2}$
Typ $D_{4}$ (mit $\mathrm {ord} (\rho )=3$ ): muss eine dritte Potenz sein, also $|K|=q^{3}$
Typ $B_{2},F_{4}$ : $|K|=2^{2m+1}$ mit $m\in \mathbb {N} _{0}$
Typ $G_{2}$ : $|K|=3^{2m+1}$ mit $m\in \mathbb {N} _{0}$

Konstruktion der getwisteten Chevalley-Gruppen

Für endliche Körper mit $q^{i}$ Elementen, eine Primzahlpotenz, gibt es also unter den oben genannten Einschränkungen zum nicht-trivialen Graphenautomorphismus $\rho$ des Dynkin-Diagramms einen entsprechenden Gruppenautomorphismus $\sigma$ gleicher Ordnung auf der zugehörigen Chevalley-Gruppe, der jede Menge $X_{r},r\in \Phi _{0}$ nach $X_{\rho (r)}$ abbildet. Mit diesem Gruppenautomorphismus wird nun wie folgt eine Untergruppe gebildet, wobei man beachte, dass die Gesamtkonstruktion nach wie vor von einer einfachen, endlichdimensionalen $\mathbb {C}$ -Lie-Algebra ausgeht und daher alle oben eingeführten Begriffe zur Verfügung stehen. Man definiert

$\Phi ^{+}:=\{r\in \Phi \mid {\text{ alle Koeffizienten in der Darstellung bzgl. der Basis }}\Phi _{0}{\text{ sind }}\geq 0\}$ , die positiven Wurzeln

$\Phi ^{-}:=\Phi \setminus \Phi ^{+}$ , die negativen Wurzeln

$U:=\langle X_{r}\mid r\in \Phi ^{+}\rangle$ , die von $\textstyle \bigcup _{r\in \Phi ^{+}}X_{r}$ erzeugte Untergruppe von $L(q^{i})$ .

$V:=\langle X_{r}\mid r\in \Phi ^{-}\rangle$

$M_{\sigma }:=\{x\in M\mid \sigma (x)=x\}$ , die Menge der $\sigma$ -Fixpunkte einer Teilmenge $M\subset L(q^{i})$ .

${}^{\mathrm {ord} \,\sigma }\!L(q^{i}):=\langle U_{\sigma },V_{\sigma }\rangle$ , die von $U_{\sigma }\cup V_{\sigma }$ erzeugte Untergruppe von $L(q^{i})$ .

Da $L(q^{i})$ definitionsgemäß von den $X_{r},r\in \Phi$ erzeugt wird, ist $L(q^{i})=\langle U,V\rangle$ und natürlich $U_{\sigma }\subset L(q^{i})_{\sigma }$ und $V_{\sigma }\subset L(q^{i})_{\sigma }$ und daher ${}^{\mathrm {ord} \,\sigma }\!L(q^{i}):=\langle U_{\sigma },V_{\sigma }\rangle \subset L(q^{i})_{\sigma }$ . Hier gilt im Allgemeinen keine Gleichheit, daher rührt die etwas kompliziert anmutende Definition.

Die Gruppen ${}^{\mathrm {ord} \,\sigma }\!L(q^{i})$ heißen getwistete Chevalley-Gruppen. Da $\mathrm {ord} \,\sigma$ nur die Werte 2 und 3 annehmen kann und nur von bestimmten Typen mit den oben genannten Einschränkungen sein kann, erhält man die restlichen Gruppen ${}^{2}\!A_{n}(q^{i}),{}^{2}\!B_{2}(2^{2m+1}),\ldots$ obiger tabellarischer Übersicht, denn es gilt folgender Satz:

Die getwisteten Chevalley-Gruppen sind einfach mit Ausnahme von

${}^{2}\!A_{2}(2^{2})$ , eine auflösbare Gruppe der Ordnung 72

${}^{2}\!B_{2}(2)$ , eine auflösbare Gruppe der Ordnung 20

${}^{2}\!G_{2}(3)$ , eine 1.512-elementige Gruppe mit einer zu $A_{1}(8)$ isomorphen Kommutatorgruppe von Index 3

${}^{2}\!F_{4}(2)$ , eine 35.942.400-elementige Gruppe mit einer Kommutatorgruppe vom Index 2.

Die Tits-Gruppe

Die getwisteten Chevalley-Gruppen ${}^{2}\!F_{4}(2^{2m+1})$ sind alle einfach bis auf die Gruppe ${}^{2}\!F_{4}(2)$ mit $m=0.$ Einfach ist aber deren Kommutatorgruppe ${}^{2}\!F_{4}(2)^{'},$ die 17.971.200 Elemente hat und zu keiner der anderen bisher aufgeführten Gruppen isomorph ist. Man nennt sie nach Jacques Tits die Tits-Gruppe. Sie gehört zur Familie der ${}^{2}\!F_{4}(2^{2m+1})^{'}$ -Gruppen von Kommutatorgruppen der ersten Familie, deren Mitglieder für m>0 als einfache nicht-abelsche Gruppen mit ihren Kommutatorgruppen übereinstimmen. Die zweite Familie besteht also ausschließlich aus einfachen Gruppen, die alle bis auf die Gruppe ${}^{2}\!F_{4}(2)^{'}$ Gruppen vom Lie-Typ sind. Definitionsgemäß wird eine endliche einfache Gruppe sporadisch genannt, wenn sie nicht einer unendlichen Familie von endlichen einfachen Gruppen zugeordnet werden kann. Somit ist die Tits-Gruppe keine sporadische Gruppe – auch wenn sie keine Gruppe vom Lie-Typ ist.

Literatur

Michael Aschbacher: Finite Group Theory. Cambridge studies in advanced mathematics (2000), ISBN 0-521-78145-0
Roger W. Carter: Simple Groups of Lie Type. John Wiley & Sons 1972, ISBN 0-471-13735-9

Basierend auf einem Artikel in:

Wikipedia.de