
Bernoulli-Gleichung
Die Bernoulli-Gleichung, die auch als Gesetz von Bernoulli oder (uneindeutig) als Satz von Bernoulli bezeichnet wird, ist eine Aussage über Strömungen nach Bernoulli und Venturi. Die Theorie über diese im Wesentlichen eindimensionalen Strömungen entlang eines Stromfadens wurde im 18. Jahrhundert von Daniel Bernoulli und Giovanni Battista Venturi angelegt und stellt die Grundlage für wichtige aero- und hydrodynamische Berechnungen dar.
Die Bernoulli-Gleichung besagt bei der stationären Strömung viskositätsfreier inkompressibler Fluide (Flüssigkeiten und Gase), dass die spezifische Energie der Fluidelemente entlang einer Stromlinie konstant ist:
Hier ist u die Geschwindigkeit, p der Betriebsdruck, ρ die Dichte, g die Schwerebeschleunigung und z die Höhe über einer Bezugsebene im Schwerefeld der Erde. Der Betriebsdruck ist derjenige Anteil am statischen Druck, der nicht aus dem Eigengewicht des Fluids resultiert. Der erste Summand stellt die spezifische kinetische Energie, der zweite die spezifische Druckenergie und der dritte die spezifische Lageenergie dar. Die auf der Stromlinie konstante spezifische Gesamtenergie e wird durch geeignete Bezugswerte auf der Stromlinie festgelegt.
Die Multiplikation der Gleichung mit der (konstanten) Dichte ρ ergibt
die Bernoullische Druckgleichung und Division durch die (konstante)
Schwerebeschleunigung g liefert eine Höhengleichung. In ihr ist die Summe
der Geschwindigkeitshöhe ,
der Druckhöhe
und der geodätischen
Höhe z (im verlustfreien Fall) konstant und gleich der
Energiehöhe
.
Instationarität der Strömung, Kompressibilität und Viskosität des Fluids können durch Erweiterungen der Bernoulli-Gleichung berücksichtigt werden. So findet sie ein breites Anwendungsspektrum in der Auslegung technischer Rohrströmungen, im Turbinen- und Windenergieanlagenbau sowie bei Messgeräten (Pitotrohr, Prandtlsonde).
Geschichte

Heute kann die Bernoulli-Gleichung aus den Navier-Stokes-Gleichungen oder dem Energieerhaltungssatz für die Fluidelemente entlang einer Stromlinie hergeleitet werden. Da diese Zusammenhänge aber erst im 19. Jahrhundert gefunden wurden, konnte Daniel Bernoulli bei seiner Herleitung 1738 nicht darauf zurückgreifen. Stattdessen benutzte er die Vorarbeiten von Evangelista Torricelli, Christiaan Huygens und Gottfried Wilhelm Leibniz.
Torricelli übertrug 1640 die Galileischen Fallgesetze auf ausströmende Flüssigkeiten, was zu Torricelli’sche Ausflussgesetz führte. Huygens erkannte 1669, dass die von René Descartes aufgestellten Gleichungen zum elastischen Stoß richtig sind, wenn man die Geschwindigkeiten unter Berücksichtigung ihres Vorzeichens zählt. Leibniz folgerte 1678 aus Huygens Gesetz des elastischen Stoßes, dass das Produkt aus Masse und dem Geschwindigkeitsquadrat, das Doppelte der kinetischen Energie, vor und nach dem Stoß identisch sind.
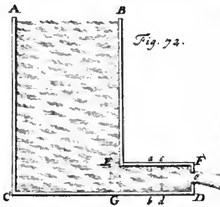
Daniel Bernoulli veröffentlichte 1738 seine Hydrodynamica, siehe Bilder, wo er in Sectio 12 die Ergebnisse von Torricelli und Huygens an einem Fluidballen (abdc in seiner Fig. 72) kombinierte. So gelang es ihm, den Druck von fließenden Fluiden auf Wänden zu bestimmen und die Rolle des Verlusts an kinetischer Energie, die er vis viva nannte, bei plötzlichen Änderungen des Strömungsquerschnitts aufzudecken.
1797 veröffentlichte der italienische Physiker Giovanni Battista Venturi seine Entdeckung, dass sich die Fließgeschwindigkeit einer Flüssigkeit, die durch ein Rohr strömt, umgekehrt proportional zu einem sich verändernden Rohrquerschnitt verhält. Venturi konnte auch experimentell nachweisen, dass der statische Druck an den Engstellen niedriger ist als an den weiteren Partien, siehe die Illustration zum Bernoulli-Effekt unten.
Bernoulli und Venturi betrachteten dabei den quasi eindimensionalen Fluss mit ebenen Querschnitten, was heute Gegenstand der Hydraulik und nicht der Hydrodynamik ist.
Eigenschaften der Strömungen nach Bernoulli und Venturi
Venturi-Effekt

Giovanni Battista Venturi entdeckte das Kontinuitätsgesetz für inkompressible Fluide: Bei gegebenem Volumenstrom A · v verhält sich die Fließgeschwindigkeit v einer inkompressiblen Rohrströmung umgekehrt proportional zum Rohrquerschnitt A, so dass der Volumenstrom über jedem Querschnitt konstant ist, siehe Bild. Dort ist Δx1,2 = v1,2 Δt und mit dem konstanten Volumen V = A1 Δx1 = A2 Δx2 folgt:
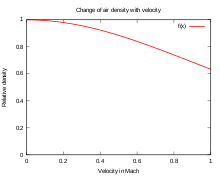
Das heißt, die Geschwindigkeit des Fluids ist dort am größten, wo der Querschnitt des Rohrs am kleinsten ist. Dieser Effekt wird umgangssprachlich Düsenwirkung genannt. Der obige Zusammenhang gilt allerdings nur solange Dichteänderungen unbedeutend sind, was bei Strömungsgeschwindigkeiten weit unterhalb der Schallgeschwindigkeit in guter Näherung gegeben ist, siehe Bild bei der Herleitung unten. Bei einer Überschallströmung in einer Düse kehrt sich der Effekt um: Ein abnehmender Querschnitt führt zu Geschwindigkeitsabnahme und umgekehrt, was in den beiden letztgenannten Artikeln erläutert und in der Lavaldüse ausgenutzt wird.
Der Venturi-Effekt macht sich im Alltag beispielsweise bemerkbar, wenn Wind zwischen Häusern an Stärke zunimmt.
Bernoulli-Effekt und hydrodynamisches Paradoxon
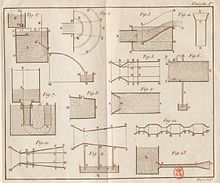
Venturi konnte experimentell auch nachweisen, was die Bernoulli-Gleichung
vorhersagte, nämlich dass an den Engstellen in der Venturi-Düse
der statische Druck abnimmt, siehe Fig. 11 im Bild. Die Kraft zur Beschleunigung
der Fluidteilchen in die Engstelle hinein ist die Druckgradientkraft
und deren Arbeit p · V (spezifisch )
führt zur Zunahme der kinetischen Energie der Fluidteilchen.
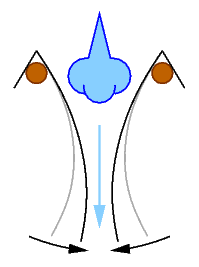
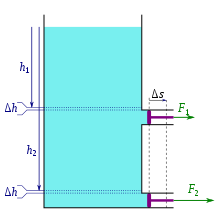
Der Sachverhalt, dass da wo die Strömung schneller ist, der Druck kleiner ist, wird Bernoulli-Effekt genannt. Dieser Effekt kann in einem einfachen Versuch gezeigt werden, siehe Versuchsskizze: Zwischen zwei über Stäbe (braun) gehängte Blätter Papier (grau) wird Luft geblasen (hellblau). Durch den höheren Umgebungsdruck gegenüber dem verringerten Druck im Luftstrom werden die Blätter zusammengedrückt (schwarz).
Diese Tatsache ist das hydrodynamische Paradoxon: Anstatt dass der eingeblasene Luftstrom die Blätter auseinanderdrückt, rücken sie zusammen. Gegenstände, die an Strömungszonen von Gasen oder Flüssigkeiten angrenzen, werden in sie hineingezogen. Auch wird ein Wasser ausstoßender Schlauch, der unter Wasser senkrecht an eine Wand gehalten wird, nicht von der Wand abgestoßen, sondern zur Wand hingezogen.
Die Stimmlippen des Menschen werden durch den Bernoulli-Effekt zu Schwingungen angeregt, was zur Stimmbildung führt. Der Bernoulli-Effekt wird in Strahlpumpen, in Schornsteinen und bei Tragflächen technisch ausgenutzt, siehe auch die Anwendung unten.
Der Bernoulli-Effekt hat jedoch auch negative Auswirkungen: Sind zwei Schiffe auf Parallelkurs, dann kann der Effekt die Schiffe derart ablenken, dass sie kollidieren. Ebenso kann ein Schiff bei schneller Fahrt und wenig Wasser unter dem Kiel auf Grund gehen, weil der Bernoulli-Effekt es in Richtung Grund saugt. Dasselbe Wirkprinzip kann bei Starkwind zu Atemnot führen, wenn der Wind infolge des Bernoulli-Effekts die in den Atemwegen ruhende Luft heraussaugt. Auch über Häuser hinwegstreichender Starkwind hat gegenüber den Räumen unter den Dachziegeln einen verringerten Druck, was zu einer Windlast führt, die Hausdächer abdecken kann.
Weitere Folgerungen aus der Bernoulli-Gleichung
Die Bernoulli-Gleichung erklärt in einer stationären, verlustfreien und inkompressiblen Strömung entlang einer Stromlinie die folgenden Tatsachen:
- Pascalsches
Gesetz: Bei konstanter Strömungsgeschwindigkeit – insbesondere in Ruhe –
sinkt der Druck mit der Höhe (oder steigt mit der Tiefe):
.
- Torricellisches
Ausflussgesetz: Bei konstantem Außendruck steigt das
Geschwindigkeitsquadrat mit abnehmender Höhe (oder zunehmender Tiefe):
.
- Venturi-Effekt: Bei horizontaler Strömung nimmt das
Geschwindigkeitsquadrat in Richtung eines Druckanstiegs ab:
.
Das Delta Δ steht für die Differenz an den Orten 1 und 2 auf der Stromlinie. Außerdem gilt beim Vergleich der physikalischen Zustände an zwei Stellen auf der Stromlinie:
- Bei gleicher Geschwindigkeit und gleichem Druck muss die Höhe an den Stellen ebenfalls gleich sein.
- Bei gleicher Geschwindigkeit und gleicher Höhe ist die Druckdifferenz an den Stellen Null.
- Bei gleichem Druck und gleicher Höhe stimmt die Geschwindigkeit an den Stellen überein.
Anwendung
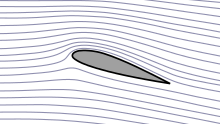
Das Bernoulli-Prinzip kann im Alltag an vielen Dingen angewendet werden. Hier einige Beispiele:
- Druckdifferenzen an einer Tragfläche werden bis zu Geschwindigkeiten von ca. 300 km/h ausreichend gut beschrieben. Wenn – wie der Grafik zu entnehmen ist – die Rauchfäden entlang der Oberseite der Tragfläche enger beieinander liegen und damit die Luft schneller strömt als in anderen Bereichen, dann impliziert die Bernoulli-Gleichung, dass der statische Druck dort geringer ist als in den anderen Bereichen. Auf der Unterseite, wo die Rauchfäden weiter auseinander liegen und damit die Luft langsamer strömt, ergibt sich entsprechend ein höherer statischer Druck. Die Bernoulli-Gleichung erklärt anhand des Stromlinienbildes die Druckdifferenzen an einer Tragfläche; sie erklärt jedoch nicht, warum die Strömung auf der Oberseite schneller ist als auf der Unterseite. (Druckdifferenzen sind eine Folge der Umlenkung der Strömung; siehe auch dynamischer Auftrieb.)
- Prandtl’sche Staurohr, das u.a. zur Geschwindigkeitsmessung eines Flugzeugs verwendet wird. Wegen der vorausgesetzten Inkompressibilität liefert es mit der gleichen Einschränkung zuverlässige Ergebnisse nur im Unterschallflug (z.B. Sportflugzeug).
- Wasserstrahlpumpe.
- Lippenbremse, eine Atemtechnik bei Asthma bronchiale und COPD.
- Ansaugtrichter eines Vergasers. Nach ihrem Erfinder sind außerdem der Venturi-Strömungsmesser und die Venturi-Düse benannt.
- Entlüften von Schiffen durch Windhutzen und Dorade-Lüfter.
- Ökologische Energieversorgung durch vertikale Windräder im Pearl River Tower (einem Hochhaus in Guangzhou).
- Der Zumischer bei der Feuerwehr dient zur Erzeugung von Schaum bei Feuerwehreinsätzen.
Für diese Anwendungen gilt:
- Da das Gesetz von Bernoulli nur entlang einer Stromlinie gilt, ist die Wirbelfreiheit im betrachteten Gebiet der Strömung zu fordern.
- Das Gesetz von Bernoulli begründet keine Kausalität, aber eine Relation zwischen Geschwindigkeits- und Druckfeld.
Klassische Formulierung für inkompressible Fluide
Energiegleichung
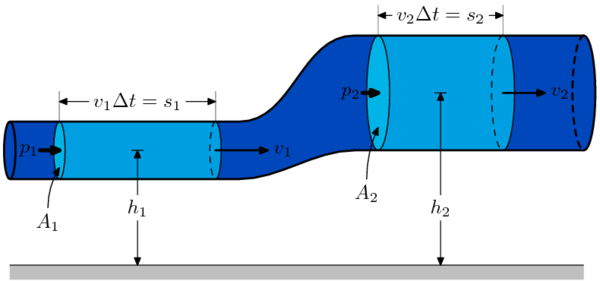
Die Bernoulli-Gleichung besteht aus drei Termen und lässt sich anschaulich an
einem Rohrleitungssystem für einen Staudamm und dem Energieerhaltungssatz
erläutern. Die Angabe der Energie erfolgt dabei als spezifische
Größe, das heißt bezogen auf die Masse des Fluids (,
pro kg in SI-Einheiten).
Den ersten Teilterm bildet die Geschwindigkeitsenergie ek (kinetische Energie) des Fluids, die sich aus der Strömungsgeschwindigkeit u ergibt. Verengt sich das Rohr steigt die Strömungsgeschwindigkeit entsprechend dem Kontinuitätsgesetz und damit die kinetische Energie.
Verläuft die Rohrleitung nun über einen Höhenunterschied z dann kommt über die Schwerebeschleunigung g die Lageenergie ep zur Geltung. Am unteren Ende des Staudamms ist die Lageenergie des strömenden Fluids geringer.
Damit gemäß dem Energieerhaltungssatz die Energie konstant bleibt, braucht es neben der Lageenergie und der kinetischen Energie einen dritten Teilterm, die Druckenergie wp. Es ist die Arbeit, die benötigt wird, um ein Teilchen von einem Gebiet mit niedrigerem Druck in ein Gebiet mit höherem Druck hineinzuschieben, wie es am unteren Ende des Staudamms der Fall ist. Je kleiner die Dichte ρ des Teilchens (großes Volumen) und je größer der Druckunterschied p, desto mehr Arbeit erfordert der Vorgang. Bei der trichterförmigen Verengung steigt durch den konstanten Volumenstrom die Strömungsgeschwindigkeit, womit das Fluid durch eine Kraft beschleunigt werden muss. Diese Kraft resultiert aus dem Druck vor der Verengung und spiegelt die Druckenergie wider, die jede Masseeinheit des Fluids, die durch das Rohr fließt, mit sich trägt. Daraus ergibt sich die eingangs angegebene Energiegleichung für inkompressible Medien
Höhengleichung
Division der Bernoulli-Gleichung durch die Schwerebeschleunigung zeigt: Bei
der stationären (zeitlich sich nicht verändernden) Bewegung einer idealen (viskositätsfreien),
inkompressiblen Flüssigkeit, die nur der Schwerkraft unterworfen ist, ist für
alle Punkte einer Stromlinie
die Summe aus Geschwindigkeitshöhe ,
Druckhöhe
und geodätischer Höhe
konstant:
Die Geschwindigkeitshöhe kann als Staudruck der Strömung verstanden werden, die Druckhöhe als Maß des Druckes der Flüssigkeit. Diese entlang der Stromlinie konstante Summe h wird als Energiehöhe bezeichnet und in Metern angegeben.
Druckgleichung
Multipliziert man die bernoullische Energiegleichung mit der Dichte ρ, erhält man die bernoullische Druckgleichung:
Der Totaldruck pt ist demnach als Summe aus
- dem Betriebsdruck p, der derjenige Anteil des statischen Drucks ist, der nicht aus dem Eigengewicht des Fluids resultiert,
- dem hydrostatischen Druck ρ g z, der das Produkt aus Dichte ρ, Erdbeschleunigung g und Höhe z ist, und
- dem dynamischen Druck ½ ρ u², der das halbe Produkt aus Dichte und Geschwindigkeitsquadrat ist,
entlang einer Stromlinie konstant. Aus der Druckgleichung ist beispielsweise ersichtlich, dass in einer Rohrleitung eine Geschwindigkeitserhöhung durch Einengung des Querschnittes aufgrund des konstanten Massenflusses im Strömungsverlauf zu einer Verminderung des Druckes führen muss, wenn die geodätische Höhe gleich bleibt.
Erweiterungen der klassischen Formulierung
Die Herleitung der Bernoulli-Gleichung aus den Navier-Stokes-Gleichungen führt auf die allgemeine Bernoulli-Gleichung in der Form
Darin sind:
- u die Geschwindigkeit
die spezifische Enthalpie bei isentroper Strömung oder p / ρ bei Inkompressibilität,
- V die spezifische Lageenergie, die im Schwerefeld der Erde die Form V = g z annimmt,
- η ein Verlustterm, der bei inkompressibler Strömung zum Druckverlust pV = ρ η und im Schwerefeld der Erde zur Verlusthöhe HV = η / g führt, und
ein Beitrag, der nur bei instationärer Strömung auftritt.
Die einzelnen Terme dieser allgemeinen Bernoulli-Gleichung sind Gegenstand der folgenden Abschnitte.
Erweiterte bernoullische Druckgleichung viskositätsfreier, idealer Gase
Die eingangs angegebene Bernoulli-Gleichung gilt nur für Fluide mit vernachlässigbarer Dichteänderung hinreichend genau. Bei Gasen und größeren Geschwindigkeitsänderungen müssen die mit der Druckänderung einhergehenden Dichteänderungen im Energieansatz berücksichtigt werden:
Für die Abhängigkeit der Dichte vom Druck stehen folgende Formulierungen zur Verfügung:
- Bei isothermer
oder isenthalper
Zustandsänderung ist
mit der spezifischen Gaskonstante Rs und der absoluten Temperatur T. Damit wird relativ zu einem Bezugspunkt 0:
-
- Darin bildet ln den natürlichen Logarithmus.
- Bei einer isentropen
oder adiabatischen
Zustandsänderung gilt
mit dem Isentropenexponent κ relativ zu einem Bezugspunkt 0 und somit
Das Differential der spezifischen Enthalpie h ist dh = T ds + v dp. Darin ist T die absolute Temperatur, s die spezifische Entropie und v = 1/ρ das spezifische Volumen. Bei isentroper Strömung (ds = 0) ist also dh = dp/ρ und der Integrand in der Bernoulli-Gleichung oben entspricht der spezifischen Enthalpie. Damit lautet die Bernoulli-Gleichung für reale Gase bei isentroper Strömung:
Darin ist
die spezifische Enthalpie.
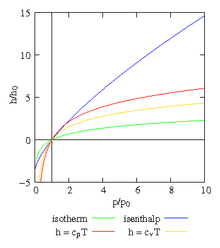
Bei druckgetriebenen Ausgleichsströmungen durch konvergierende Düsen gelten
die folgenden Zusammenhänge.
Die spezifische Enthalpie
für ein ideales Gas ist h = cp T und mit den in idealen
Gasen anzutreffenden Zusammenhängen
folgt:
Darin sind cp,v die spezifischen Wärmekapazitäten des Gases bei konstantem Druck bzw. konstantem Volumen.
Das Bild zeigt die Enthalpiebeiträge h / h0 mit h0 = Rs T von Luft gemäß den angegebenen Formeln und isentroper Zustandsänderung (außer bei der isothermen Zustandsänderung) relativ zum Bezugspunkt 0 unter Normalbedingungen
Bei der orangen Kurve „h = cv T“ ist
und wie bei der roten Kurve „h = cp T“ wurde
benutzt.
Erweiterte bernoullische Energiegleichung zäher Flüssigkeiten
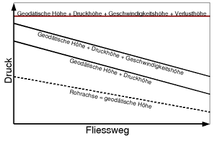
Die erweiterte bernoullische Energiegleichung setzt sich mit zähen
Flüssigkeiten auseinander. Dabei werden die Reibungsverluste berücksichtigt. Die
so genannte Verlusthöhe HV wird empirisch meist durch
einen Druckverlustbeiwert
(Zeta) mit
folgender Funktion berechnet:
mit
- ζ: Druckverlustbeiwert
- u: Geschwindigkeit
- g: Schwerebeschleunigung (also Lageenergie V = g z)
Diese Annahme fußt auf der empirischen Beobachtung, dass die Druckverluste in Rohrleitungen bei turbulenter Strömung mit dem Quadrat der Fließgeschwindigkeit steigen. Die Verlustbeiwerte oder die Summe der Verlustbeiwerte in einem Gesamtsystem setzen sich zusammen aus:
- Einzelverlusten wie Ein- und Auslaufverlust, Einbautenverlust (Krümmer, Einengungen, Schieber) und
- Verlusten aus der Rohrreibung
Die um den Druckverlust ρ g HV erweiterte Druckgleichung lautet daher:
Mit dieser Gleichung können bei Kenntnis der Verlustbeiwerte die üblichen Fragen der Bemessung von Rohrleitungssystemen mit turbulenter Strömung gelöst werden.
Für die Berechnung der Energieverluste wäre zwischen Einzelverlusten und Verlusten in geraden Rohren zu unterscheiden.
Einzelverluste
Diese werden nach der Formel
berechnet. Die Druckverlustbeiwerte ζ betragen beispielhaft
- bei Einläufen in Rohrleitungen:
-
- ζ = 0,50 (senkrechter Einlauf, scharfkantig),
- ζ = 0,06 bis 0,005 (senkrechter, abgerundeter Einlauf),
- bei plötzlicher Querschnitterweiterung F1 → 2
-
- oder
- bei allmählicher Verengung (Winkel der Verengung < 20°)
-
- ζ = 0,04.
Der Parameter ζ wird nach empirischen Formeln bestimmt, die von der Rauheit der Rohrleitung und dem Fließverhalten des Mediums abhängen.
Verluste in geraden Rohrleitungen
Diese werden nach der sogenannten Darcy-Weisbach-Gleichung zu
: Energieliniengefälle, das heißt Verlusthöhe je Längeneinheit der Rohrleitung.
: Rohrreibungszahl (Verlustbeiwert)
: Rohrdurchmesser
berechnet.
Erweiterte bernoullische Energiegleichung für instationäre Strömungen
Der Beitrag von Geschwindigkeitsänderungen mit der Zeit wird in der Bernoulli-Gleichung üblicher Weise unterschlagen, kann aber berücksichtigt werden:
Das Integral der lokalen Beschleunigung
entlang der Stromlinie zwischen den Punkten 1 und 2 wird zu einem
festgehaltenen Zeitpunkt ausgewertet, siehe dazu das Beispiel unten.
Eine wesentliche Vereinfachung erfährt die Gleichung, wenn die Strömung verlust- und rotationsfrei ist oder – gleichbedeutend – eine Potentialströmung ist. Dann gibt es ein Geschwindigkeitspotential φ, dessen Gradient die Geschwindigkeit ist. In einer solchen Strömung gilt die erweiterte Bernoulli-Gleichung
sogar global, also für beliebige Punkte im Strömungsfeld. Die zu einem
Zeitpunkt im gesamten Strömungsfeld konstante Größe C könnte noch von der
Zeit abhängen aber diese Zeitabhängigkeit kann dem Potential φ
zugeschlagen werden, ohne dass sich dessen physikalische Bedeutung
ändern würde.
Herleitung
Herleitung aus dem Energiesatz
Die Bernoulli-Gleichung kann aus der Energiebilanz abgeleitet werden, die erfordert, dass in einer stationären Strömung zur Änderung der Energie eines Fluidelements Arbeit verrichtet werden muss. Die Arbeit ist die des Drucks und die Energien sind die Lageenergie und die kinetische Energie. Es zeigt sich dann, dass die Summe aus der Druckarbeit (etwas ungenau Druckenergie), der kinetischen und der Lageenergie entlang einer Stromlinie konstant ist.
| Herleitung über die Energiebilanz |

Fluidballen
(hellblau) in einem Stromfaden (königsblau) |
Die Energiebilanz besagt, dass zur Änderung der Energie der
Fluidelemente Arbeit verrichtet werden muss:
Darin ist W die mechanische Arbeit, die aufgewendet werden muss,
um die Energiedifferenzen ΔEpot/kin zwischen den
Zuständen 2 (nachher) und 1 (vorher) zu erzeugen.
Die Differenz der Lageenergie nachher und vorher ist
mit den Höhen h1,2. Die Differenz der kinetischen
Energie nachher und vorher ist
mit den Geschwindigkeiten u1,2. Einsetzen dieser
Zwischenergebnisse in die Energiebilanz liefert:
Division durch das Volumen V und Umstellung führt auf die
Bernoulli-Gleichung:
|
Herleitung aus den Navier-Stokes-Gleichungen
Heute kann die Bernoulli-Gleichung bei einem barotropen, Newton’schen Fluid in einem konservativen Schwerefeld aus den Navier-Stokes-Gleichungen hergeleitet werden. Die getroffenen Voraussetzungen gestatten die Vorabintegration der in den Navier-Stokes-Gleichungen vorkommenden Gradienten entlang einer Stromlinie, was auf die Bernoulli-Gleichung führt. Da die Druck-Dichte-Relation bei Gasen temperaturabhängig ist – Gase allgemein nicht barotrop sind – und Flüssigkeiten oft in guter Näherung inkompressibel sind, wird zumeist Inkompressibilität vorausgesetzt. Diese ist bei Strömungen weit unterhalb der Wellenausbreitungsgeschwindigkeit im Fluid in guter Näherung gegeben, siehe Bild.
| Herleitung aus den Navier-Stokes-Gleichungen |
| Betrachtet wird die Strömung eines barotropen, Newton’schen Fluids in
einem konservativen Schwerefeld. Newton’sche Fluide gehorchen den
Navier-Stokes-Gleichungen Darin ist In einem inkompressiblen Fluid ist die Dichte konstant und P = p /
ρ. In einem konservativen Beschleunigungsfeld Bei Integration dieser Gleichung zu einer festgehaltenen Zeit
t entlang einer Stromlinie
Der Verlustterm η ist für reale Strömungen zwar nur schwer exakt
bestimmbar, lässt sich aber abschätzen.
Für eine ortsabhängige Funktion Die Indizes 1 und 2 markieren die Werte an den Stellen Nach Umstellung entsteht die im Text angegebene erweiterte
Bernoulli-Gleichung: In einer stationären Strömung entfällt das verbliebene Integral auf der
rechten Seite, in viskositätsfreien Strömungen verschwindet der
Verlustterm η, im Schwerefeld der Erde ist V = g z und bei
Inkompressibilität ist P = p / ρ. |
Beispiel

Ein Behälter wie im Bild befinde sich im homogenen Schwerefeld der Erde mit Schwerebeschleunigung g sowie Umgebungsdruck p0 und sei mit einer idealen, inkompressiblen Flüssigkeit mit Dichte ρ gefüllt. Die Höhendifferenz zwischen der Oberfläche AB und dem Ausfluss o zwischen F und D sei h und der Durchmesser FD sei gegenüber der Oberfläche AB und der Höhe h vernachlässigbar klein. Zur Zeit t0 = 0 werde der Ausfluss geöffnet, so dass der Behälter in einer instationären Strömung ausläuft, wobei der Füllstand des Behälters durch einen Zufluss konstant gehalten werde. Gesucht ist die Ausströmungsgeschwindigkeit im Abflussrohr als Funktion der Zeit.
Zu einem Zeitpunkt t > t0 verbindet ein Stromfaden die Oberfläche AB (Punkt 1) und den Ausfluss o (Punkt 2). Die Geschwindigkeit im Behälter ACGB kann wegen des kleinen Durchmessers FD gegenüber AB vernachlässigt werden und die Geschwindigkeit auf den Querschnitten im Abflussrohr zwischen EG und FD (über die Distanz L) ist überall gleich u und ebenso ist ihre Änderung ∂u/∂t im Abflussrohr konstant. Die erweiterte Bernoulli-Gleichung für instationäre Strömungen liefert somit:
Diese nichtlineare gewöhnliche Differentialgleichung erster Ordnung kann durch Trennung der Variablen gelöst werden:
Darin ist artanh der
Areatangens
Hyperbolicus und tanh seine Umkehrfunktion
Tangens
Hyperbolicus. Die Geschwindigkeit hat zur Zeit t = 0 den Wert Null
und erreicht für t → ∞ asymptotisch den Grenzwert ,
was das Torricelli’sche
Ausflussgesetz darstellt.
Dieses Gesetz ergibt sich aus der Bernoulli-Gleichung schneller mit der Annahme einer stationären Strömung:
Siehe auch
Bernoulli-Effekt:


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 30.03. 2024