Dynamischer Auftrieb

Der dynamische Auftrieb ist eine zentrale Größe in der Strömungslehre. Er ist der Anteil der auf einen umströmten Körper wirkenden Kraft, der senkrecht zur Anströmrichtung steht. Der dynamische Auftrieb ist das physikalische Grundprinzip für das natürliche Fliegen von Vögeln, Fledertieren und Fluginsekten sowie die technische Funktion der Tragflächen von Flugzeugen, der Propeller, der Schiffsschrauben, der Schratsegel und der Turbinen. Manchmal wird in geringem Maße dynamischer Auftrieb (oder Abtrieb) auch von Luftschiffen genutzt, um kein Traggas ablassen oder Ballast abwerfen zu müssen; auch manche Typen von Fesselballonen und Kitoons nutzen in geringem Maße dynamischen Auftrieb.

Die Entstehung von Auftrieb aus horizontaler Anströmung wird mit der Methodik der Hydrodynamik erklärt. Diese ist Teil der klassischen Mechanik und gehorcht deshalb den Newtonschen Gesetzen und den hieraus abgeleiteten Erhaltungssätzen (Impuls- und Energieerhaltung). Bei kompressiblem Medium (Gas) ist außerdem eine thermodynamische Betrachtung der Vorgänge erforderlich.

Auftrieb entsteht bei Umströmung entsprechend geformter Körper, z. B. Tragflächen. Hierbei wird die Luft nach unten umgelenkt, also beschleunigt. Der abwärts gerichteten Kraft auf die Luft entspricht als Gegenkraft die aufwärts gerichtete Kraft auf die Tragfläche, der Auftrieb. Auftriebskräfte können auch in Richtung Erdboden wirken und werden dann als Abtrieb bezeichnet. Bei Rennfahrzeugen kann so mit Hilfe von Front- und Heckflügeln Anpressdruck erzeugt werden.

Einführung

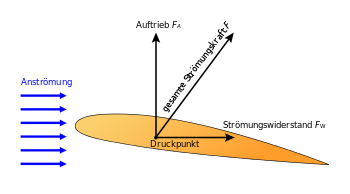
Skizze des dynamischen Auftriebs F_A und des Strömungswiderstands F_W an einer angeströmten Tragfläche.

Bei der Bewegung eines Körpers einer bestimmten Form und Position relativ zu einem Gas oder einer Flüssigkeit wirken auf den Körper Kräfte, die durch die Umströmung hervorgerufen werden (Bernoulli-Effekt). Im Gegensatz zum statischen Auftrieb ist die Richtung des dynamischen Auftriebs nicht durch die Schwerkraft definiert, sondern durch die Richtung der Anströmung. Die gesamte Strömungskraft wird in zwei Komponenten zerlegt: in den Widerstand in Anströmrichtung und den Auftrieb senkrecht dazu.

Bei der Bewegung eines Körpers einer bestimmten Form und Orientierung relativ zu einem Gas oder einer Flüssigkeit wirken auf den Körper Kräfte, die durch die Umströmung hervorgerufen werden. Im Gegensatz zum statischen Auftrieb ist die Richtung des dynamischen Auftriebs nicht durch die Schwerkraft definiert, sondern durch die Richtung der Anströmung. Die resultierende Strömungskraft greift am Druckpunkt an und kann in zwei Komponenten zerlegt werden, in den Widerstand in Anströmrichtung und den Auftrieb senkrecht dazu.

Der dynamische Auftrieb $F_\mathrm{A}$ ist der senkrecht zur Anströmung wirkende Anteil der resultierenden Luftkraft:

$F_{{\mathrm {A}}}=c_{{\mathrm {A}}}\,{\frac {\rho }{2}}\,v^{2}\,A$
Der parallel zur Anströmung wirkende Teil der resultierenden Luftkraft ist der Strömungswiderstand $F_\mathrm{W}$ .

$F_{{\mathrm {W}}}=c_{{\mathrm {W}}}\,{\frac {\rho }{2}}\,v^{2}\,A$

Dabei bedeuten:

$c_{{\mathrm {A}}}$ der Auftriebsbeiwert,

$c_{\mathrm {W} }$ der Widerstandsbeiwert,

$\rho$ die Dichte des Mediums,

die Anströmgeschwindigkeit des Mediums,

die Referenzfläche (bei Auftriebs- oder Tragflächen die Flügelfläche, nicht die Querschnittsfläche in Strömungsrichtung).

Die Koeffizienten Auftriebsbeiwert $c_{{\mathrm {A}}}$ und Widerstandsbeiwert $c_{\mathrm {W} }$ sind von der Form und Orientierung des Körpers in der Strömung abhängig. Bei Tragflächen werden Form und Orientierung als Profil und Anstellwinkel ${\alpha }$ bezeichnet. Der Anstellwinkel ${\alpha }$ ist der Winkel zwischen der Profilsehne der Tragfläche und der Strömungsrichtung des Mediums. Der dynamische Auftrieb $F_\mathrm{A}$ an einer Tragfläche (mit ihrem gegebenen Profil) wird also vom Anstellwinkel $\alpha$ der Tragfläche und ihrer Fläche sowie der Dichte $\rho$ des Mediums und seiner Strömungsgeschwindigkeit bestimmt.

Funktionsprinzip

Für Grundüberlegungen zum Verständnis des Auftriebs wird der Luftraum aus kubischen, luftgefüllten Raumelementen zusammengesetzt. Jedes dieser Luftvolumina muss von seiner Umgebung getragen werden, sonst würde es zum Erdboden stürzen:

Volumina, die nur Luft enthalten, werden durch den statischen Auftrieb nach Archimedes von der Umgebung getragen. Die Druckdifferenz zwischen der unteren Fläche und der oberen Fläche eines Volumens, die sich durch die Druckabnahme mit zunehmender Höhe ergibt, ist die Gegenkraft zur Schwerkraft (siehe auch hydrostatischer Druck).
Volumina, die das Flugzeug (den Vogel,…) ganz enthalten, müssen mitsamt dem Flugzeug von ihrer Umgebung getragen werden. Die folgenden Ausführungen zeigen, dass hierfür innerhalb des Volumens auf die Luft ein Impuls nach unten erzeugt wird. Die Gegenkraft der Impulsproduktion ist der Auftrieb. Dieser Impuls bleibt erhalten.

Leicht nachvollziehbare Experimente unterstützen dieses Erklärungsmodell:

Der Tischventilator bläst ständig Luft fühlbar in erstaunlich große Entfernungen.
Eine Postkarte, horizontal und mit Anstellwinkel über eine Kerze bewegt, bringt deren Flamme auch aus erstaunlich großer Höhe zum Flackern.

Auch in Entfernungen, in denen diese Effekte nicht mehr spürbar sind, gilt der Satz der Impulserhaltung, nach dem sich der Impuls nur unter Einfluss von Kräften ändert. Vermischt sich zum Beispiel vom Ventilator abgeblasene Luft mit der Umgebung, ist dieser Prozess impulserhaltend. Durch die Vermischung ist wohl eine größere Masse Luft am Impuls beteiligt, weshalb die Strömungsgeschwindigkeit sinkt. Es wirkt aber keine Kraft auf diese Luft, weswegen der Impuls als Ganzes erhalten bleibt.

Zur Wahrung der Energieerhaltung bei Durchmischung ist zu beachten, dass durch die Abnahme der mittleren Strömungsgeschwindigkeit zwar die kinetische Energie abnimmt. Gleichwohl wird diese kinetische Energie in thermische Energie umgewandelt, wodurch die Energie als Ganzes erhalten bleibt.

Ein Analogon hierzu aus der Schulphysik ist der unelastische Stoß.

Am Auftrieb beteiligte physikalische Größen

Dieses Kapitel beschreibt zunächst das Strömungsfeld um eine Tragfläche. Hiernach werden die wichtigsten Kräfte und ihr Beitrag zum Auftrieb diskutiert.

Das Strömungsfeld

Strömungsfeld um ein Tragflächenprofil. Medium unterhalb des Profils bleibt im Vergleich zu dem auf der Oberseite zurück.

Ein Tragflächenprofil, das ein Medium mit einem geeigneten Anstellwinkel durchquert, schiebt das Medium nicht nur zur Seite. Zusätzlich wird das Medium tangential zur Bewegung beschleunigt. Auf der Unterseite erfolgt eine leichte Beschleunigung in Richtung der Bewegung wie bei einer Bugwelle. Viel stärker ist auf der Oberseite des Profils eine Beschleunigung gegen die Bewegungsrichtung, also nach hinten.

Der Einfluss des Profils ist am stärksten nahe der Oberfläche. Dies führt dazu, dass benachbarte Pakete des Mediums, die von der Vorderseite des Profils getrennt wurden, hinter dem Profil nicht wieder zusammen kommen. Vielmehr bleiben sie auf Dauer getrennt – im nebenstehenden Beispiel einer simulierten Strömung um fast eine Profiltiefe. Dieser Versatz des oben strömenden Mediums gegenüber dem unteren lässt sich mit gepulsten Rauchfahnen experimentell beobachten.

Der Druck

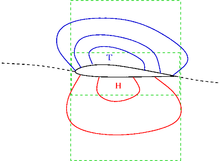
Druckfeld um einen Flügel (schematisch)

Die Skizze rechts zeigt das Druckfeld um einen Flügel. Es ist charakterisiert durch tiefen Druck über dem Flügel mit zunehmendem Druck nach oben und hohem Druck unter dem Flügel mit abnehmendem Druck nach unten. Dieses Druckfeld übt daher auf die hier befindliche Luft eine Kraft nach unten aus.

Das Bild zeigt weiterhin zwei Volumina (grün gestrichelt), die jeweils das Flugzeug enthalten. Ober- und unterhalb des kleinen, zentralen Volumens befinden sich zwei Volumina, die das Flugzeug nicht enthalten. Die vertikalen Druckkräfte auf jedes Volumen ergeben sich aus der Druckverteilung auf den horizontalen Randflächen:

Das kleine, zentrale Volumen erhält durch den Druck kräftigen Auftrieb. Die Druckunterschiede zwischen der oberen und unteren Begrenzungsfläche sind groß.
Entsprechend hat das große Volumen nur schwachen bis unmerklichen Auftrieb. Die Ränder sind so weit vom Flügel entfernt, dass fast kein Druckunterschied mehr existiert.
Die beiden Volumina, die das Flugzeug nicht enthalten, erfahren durch den Druck Abtrieb.

Auf diese Weise lassen sich beliebig – auch vor und hinter dem Flügel – Volumina nach dem Bausteinprinzip zusammenstellen. Die jeweilige Druckkraft wird im Allgemeinen immer individuell für jedes Volumen differieren. Alleine daher ist die Druckkraft zur Beschreibung des Auftriebs eines Flugzeugs ungeeignet.

Mit zunehmender Entfernung nimmt die Änderung des Luftdrucks durch den Flügel ab. Dies erlaubt die Definition eines Einflussbereichs als das Gebiet um den Flügel, innerhalb dessen der Druck einen signifikanten Anteil am Gesamtauftrieb hat. Dieser Einflussbereich ist in jedem Falle klein (vielleicht bis zu 100 m bei Verkehrsflugzeugen) im Verhältnis zur erreichbaren Flughöhe von bis zu 20 km. Hiermit begründet sich, dass die Druckkraft in der Zusammenfassung nicht genannt ist. Eine prinzipiell maximale Flughöhe gibt es darüber hinaus nicht.

Gleichwohl gibt es in der integrierten Bewegungsgleichung noch als zweiten Term zur Kompensation der Gewichtskraft des Flugzeugs die Impulsproduktion der Luft, aus der nach Integration der Impulsfluss durch die Volumenoberfläche wurde.

Der Impulsfluss

Strömungsablenkung durch Tragflächenprofil

Gelangen Luftteilchen in den oben definierten Einflussbereich des Flügels, werden sie dem dort nach unten abnehmenden Druck entsprechend nach unten beschleunigt. Entsprechend ihrer Masse wird also Vertikalimpuls produziert. Nach Verlassen des Einflussbereiches wirkt keine Kraft mehr auf die Luftteilchen – ihr Impuls bleibt erhalten.

Integriert man dies über ein ortsfestes Volumen, wird aus der Impulsproduktion der Teilchen der Impulsfluss durch die gesamte Oberfläche des Volumens.

Auf Volumina ohne Flugzeug übt das Druckfeld insgesamt eine Kraft aus, wenn sie teilweise im Einflussbereich des Flügels sind – im Allgemeinen nach unten. Da diese jedoch im Sinne dieses Artikels kräftefrei sind, und keine weiteren Kräfte vorhanden sind, ist die Impulsproduktion und damit der Impulsfluss aus dem Volumen heraus die Gegenkraft zur Druckkraft.

Bei Volumina mit Flugzeug wird das Flugzeug grundsätzlich von der Summe aus Druckkraft und Impulsproduktion (-fluss) getragen. Da die Druckkraft mit größer werdendem Volumen klein wird, bleibt im Allgemeinen nur der im Einflussbereich produzierte Impuls, der nach Verlassen des Einflussbereichs erhalten bleibt. Diese Impulsproduktion ist somit die Gegenkraft, die das Flugzeug trägt.

Die Viskosität

Umströmung eines Flügels für

Viskosität → Null oder
Reynolds-Zahl → unendlich

Die Viskosität der Luft wurde in der bisherigen Diskussion weitgehend ausgeklammert. Es wurde auch nur gezeigt, dass die Umströmung des Flügels im Allgemeinen durch Produktion von Vertikalimpuls die Gegenkraft zur Gewichtskraft des Flugzeugs bildet. Es wurde jedoch ausgeklammert, warum die Luft dies tut, und die Strömung nicht z. B. wie in der Skizze ähnlich wie bei Umströmung einer quer zur Strömung stehenden Platte verläuft und dabei keinen Auftrieb liefert.

Viskose Effekte spielen nur in der Grenzschicht des Flügels eine wichtige Rolle. Diese ist auch bei Verkehrsflugzeugen nur wenige Zentimeter dick. Über die vertikale Scherung der Horizontalströmung durch die Viskosität in der Grenzschicht hat die Strömung hier die Tendenz, in Strömungsrichtung sanft gebogenen Oberflächen zu folgen. Direkt an der Oberfläche ist die Geschwindigkeit exakt Null. Sie wird größer mit zunehmendem Abstand von der Oberfläche, bis sie die Fluggeschwindigkeit erreicht. Durch diese Scherung hat die Luft in der Grenzschicht eine Wirbelstärke. Die Viskosität bewirkt Kräfte, durch die die Geschwindigkeiten benachbarter Stromlinien angeglichen sowie die Wirbelstärke homogenisiert werden.

Die Kausalkette zum Auftrieb

Verlässt nun ein Teilchen mit seiner Wirbelstärke wegen der gebogenen Oberfläche die Grenzschicht tangential, wird die Viskosität die Scherung des Geschwindigkeitsfeldes homogenisieren und die Wirbelstärke bleibt auf einem mittleren Wert. Mangels Scherung erzwingt sie eine gekrümmte Trajektorie in Richtung zurück zur Oberfläche. Als Gegenkraft hierzu verringert sich der Druck an der Oberfläche. Dieser niedrige Druck beschleunigt auch Luft oberhalb der Grenzschicht nach unten. Der Druck ist auch niedriger als der Druck entlang des Flügel stromaufwärts. Deshalb wird die Strömung auch tangential über den Flügel nach hinten beschleunigt.

Energieerhaltung

Bislang wurde kein Unterschied gemacht zwischen kompressibler und inkompressibler Strömung. Für die Betrachtung der Impulsbilanz unter dem Einfluss von Kräften ist diese Unterscheidung auch unwichtig. Bei der Betrachtung der Energetik ist jedoch die Arbeit gegen Volumenänderung wichtiger Bestandteil bei kompressibler Strömung. Hier wird jedoch weiterhin Stationarität aus Sicht des Flugzeugs und Reibungsfreiheit (außerhalb der Grenzschicht) angenommen.

Inkompressibilität

Für inkompressible, stationäre Strömung konstanter Dichte gilt zunächst entlang einer Trajektorie das Gesetz von Bernoulli: Die Summe aus dem Quadrat der Geschwindigkeit und dem Quotient aus Druck und Dichte ist konstant. Für Luftteilchen, die in den Einflussbereich des Flügels gelangen bedeutet dies:

Bei Druckabnahme über dem Flügel nimmt die Strömungsgeschwindigkeit zu.
Bei Druckzunahme unter dem Flügel nimmt die Strömungsgeschwindigkeit ab.

Das Gesetz von Bernoulli macht keine Aussage über Ursache und Wirkung, sondern es beschreibt nur eine Relation zwischen Druck- und Geschwindigkeitsfeld. Das Gesetz von Bernoulli folgt unmittelbar aus dem Prinzip der Energieerhaltung. Hierbei ist das Druckfeld ein Potential der Kraft.

Kompressibilität

Nebelbildung im Unterdruckbereich der Tragflächen eines Flugzeuges

Bei Umströmung eines Tragflügels kann mit hinreichender Genauigkeit Inkompressibilität angenommen werden, wenn die Fluggeschwindigkeit klein gegenüber der Schallgeschwindigkeit ist. Beim Verkehrsflug und großen Teilen des Militärfluges muss jedoch die Kompressibilität berücksichtigt werden.

Bei Druckänderung entlang einer Trajektorie ist eine Geschwindigkeitsänderung nach Bernoulli daher nicht mehr die einzige Variante, um die Energieerhaltung zu erzwingen. Alternativ hat die Luft die Möglichkeit, ihr Volumen zu vergrößern, bzw. die Dichte zu verringern. Hierbei wird Arbeit verrichtet, die durch Verringern der inneren Energie, also bei Abwesenheit von Wärmequellen durch adiabatische Abkühlung kompensiert wird. Auf diese Weise kann es zu Kondensation und Nebelbildung über der Tragflügeloberseite kommen (Bild rechts).

Andere Erklärungsmodelle

Die Zirkulation – der Beobachter am Boden

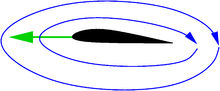
Zirkulationsströmung um einen Flügel

Der Beobachter am Boden sieht ein Flugzeug durch ruhende Luft fliegen. Die Strömung aus seiner Sicht ergibt sich durch vektorielle Addition der überall gleichen Fluggeschwindigkeit (Skizze, grüner Pfeil) zu der bisher aus Sicht des Flugzeugs betrachteten Strömung:

Oberhalb des Flügels ist die Strömung aus Sicht des Flugzeugs schneller als die Fluggeschwindigkeit. Der Beobachter am Boden sieht daher eine Strömung nach hinten entgegen der Flugrichtung.
Unterhalb des Flügels ist die Strömung aus Sicht des Flugzeugs langsamer als die Fluggeschwindigkeit. Der Beobachter am Boden sieht daher eine Strömung nach vorne in Flugrichtung.
Das Druckfeld bewegt sich wie bisher betrachtet mit dem Flügel mit und bewirkt aus Sicht des am Boden stehenden Beobachters eine Vertikalbewegung direkt hinter dem Flügel nach unten.
Aus Gründen der Massenerhaltung gibt es immer eine Vertikalbewegung nach oben vor dem Flügel. Wegen der großen Fläche, auf die sie verteilt ist, hat sie für den Auftrieb keine Bedeutung.

Das Ergebnis ist die Zirkulationsströmung, wie sie in der Abbildung durch Stromlinien skizziert ist. Eine Stromlinie erhält man aus einer Momentaufnahme durch Verbinden aller Punkte in Richtung der Strömung in diesem Punkt und zu dem betrachteten Zeitpunkt. Stromlinien sind immer geschlossen oder sie enden am Rand des betrachteten Gebietes. Aus Sicht des Flugzeugs erhält man die gleiche Zirkulation aus der Geschwindigkeitsdifferenz der Strömung über und unter der Tragfläche.

Diese Zirkulation wird häufig zur Erklärung des Auftriebs verwendet. Hierbei wird die Bildung der Zirkulation als Gegenwirbel zum hinter dem Flügel beobachteten Anfahrwirbel erklärt und damit begründet, dass die Gesamtzirkulation aus Anfahrwirbel und Zirkulationsströmung Null sein muss (Helmholtzscher Wirbelsatz). Mathematisch liefert diese Methode in 2D auch gute Ergebnisse, zur vollständigen Erklärung des Auftriebs ist sie jedoch unzureichend:

Sie reduziert das Problem auf zwei Dimensionen, weil der zugrundeliegende Integralsatz von Stokes dies erfordert.
Der Helmholtzsche Wirbelsatz sagt nichts über Ursache und Wirkung der beteiligten Wirbel. Im vorliegenden Fall ist der Anfahrwirbel der Gegenwirbel zur Zirkulationsströmung um den Flügel. Für die Stärke des Wirbelpaares wird die empirische Kutta-Bedingung herangezogen, nach der die Zirkulation um den Flügel so ist, dass Strömung an der scharfkantigen Endleiste glatt abströmt.

Das mathematische Modell einer wirbelfreien Zirkulationsströmung um den mit Fluggeschwindigkeit fliegenden Flügel liefert jedoch in vielen Fällen gute quantitative Ergebnisse für den Auftrieb. Dies gilt besonders für Flügel mit großer Streckung im Unterschallbereich, also z.B. Segelflugzeuge. Der Grund liegt in der Ähnlichkeit der Vereinfachungen einer allgemeinen Strömung, damit diese nach Bernoulli oder als wirbelfreie Potentialströmung beschrieben werden kann.

Die genannte Kutta-Bedingung erfüllt zwar ihren Zweck bei der praktischen Berechnung des Auftriebs, ist aber physikalisch nicht begründbar . Die physikalisch korrekte Begründung liegt in der Viskosität der Luft, durch die die Luft in der wenige Millimeter dicken Grenzschicht gezwungen wird, sanft gebogenen Oberflächen zu folgen. Als Folge strömt die Luft an der scharfen Endleiste entsprechend der Kutta-Bedingung ab.

Zu Bernoulli

Die Bernoulli-Gleichung ist eine stark vereinfachte Form der Navier-Stokes-Gleichungen. Sie gilt entlang einer Trajektorie bei stationärer, inkompressibler und viskositätsfreier Strömung in einem Gebiet, das keine Wirbel enthält. Wegen dieser Einschränkungen ist die Bernoulli Gleichung nur sehr eingeschränkt zur Erklärung von Strömungen zur Auftriebsgewinnung geeignet:

Insekten- und Vogelflug scheiden aus, weil die Umströmung der Flügel durch Flügelschlag nicht stationär ist.
Verkehrs- und Militärflug scheiden aus, weil hier die Schallgeschwindigkeit erreicht oder überschritten wird. Die Kompressibilität ist somit zwingend zu berücksichtigen.

Beim klassischen Segel-, Motor und auch Modellflug sowie dem Segelflug der Vögel sind in der Umströmung der Flügel außerhalb der Grenzschicht die Bedingungen zur Anwendung der Bernoulli-Gleichung erfüllt. Sie gibt jedoch keine Aussage über Ursache und Wirkung, sondern beschreibt nur den Zusammenhang zwischen Druck- und Geschwindigkeitsfeld.

Stationäre und instationäre Strömungen

Bei stationärer Strömung gilt 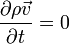$\frac{\partial \rho \vec v}{\partial t} = 0$ , was die Umströmung aus Sicht des Flugzeugs sehr gut beschreibt. Bei stationärer Strömung (z. B. eines Flugzeugs) wird das Gewicht des Flugzeugs demnach nur durch Oberflächenkräfte, also durch die Randbedingungen des betrachteten Volumens, balanciert. Volumina hierzu sind beliebig groß, haben jedoch die Einschränkung, für diese Diskussion zeitlich konstant zu sein aus Sicht des Flugzeugs. Vogelflug (mit Flügelschlag) kann damit nicht diskutiert werden. Auch bei zeitlicher Mittelbildung über die Periode eines Flügelschlages ist wegen der Nicht-Linearität des Impulsflusses dieser Term sehr vorsichtig zu diskutieren.

Bei Stationarität sind auch rotierende Tragflächen (Rotoren von Helikoptern, Propeller, Tischventilatoren) bei dieser Form der Bewegungsgleichung zunächst ausgeschlossen. Im dann rotierenden Bezugssystem sind die Trägheitskräfte Zentrifugal- und Corioliskraft auf ihre Wichtigkeit im Kräftespiel zu diskutieren. Diese Kräfte stehen jedoch lotrecht zur Rotationsachse und spielen daher bei der Diskussion des Auftriebs keine Rolle, weil diese Kräfte parallel zur Rotationsachse zeigen.

Als mathematisches Modell zur Beschreibung des instationären Falles verwendet man dann die Euler- oder Navier-Stokes-Gleichungen.

Basierend auf einem Artikel in:

Wikipedia.de