Hydrostatischer Druck

Der hydrostatische Druck (altgriechisch ὕδωρ hýdor, deutsch ‚Wasser‘), auch Gravitationsdruck oder Schweredruck, ist der Druck, der sich innerhalb eines ruhenden Fluids, das ist eine Flüssigkeit oder ein Gas, durch den Einfluss der Gravitation einstellt. In geschlossenen Gefäßen kann ein konstanter hydrostatischer Druck auch im schwerelosen Raum auftreten. Der Begriff wird entgegen der Wortbedeutung „Wasser“ auch für andere Flüssigkeiten und sogar für Gase verwendet, da er jene Art von Spannungstensoren darstellt, die ebenso in ruhendem (somit schubspannungsfreien) Wasser auftritt.

Dynamischer Druck durch Fluidströmungen wie z.B. der Staudruck wird vom hydrostatischen Druck nicht erfasst.

Inkompressible Flüssigkeiten im homogenen Schwerefeld

Pascal’sches Gesetz

Mit der Wassertiefe steigt der Druck. Zum hydrostatischen Druck hinzu kommt noch der Luftdruck an der Wasseroberfläche. Zu beachten sind die verschiedenen Maßstäbe an der y-Achse: In der Wassersäule steigt der Druck viel schneller an als in der Luftsäule.

Der hydrostatische Druck am Boden ist trotz unterschiedlicher Füllmengen in allen drei Gefäßen gleich groß.

Der hydrostatische Druck für Fluide mit konstanter Dichte im homogenen Schwerefeld (= Inkompressible Fluide, insbesondere Flüssigkeiten) berechnet sich nach dem Pascal’schen (oder pascalschen) Gesetz (benannt nach Blaise Pascal):

$p(h)=\rho gh+p_{0}$

Formelzeichen:

$\rho$ = Dichte [für Wasser: $\rho$ ≈ 1.000 kg/m³]

= Schwerebeschleunigung [für Deutschland: ≈ 9,81 m/s²]

= Höhe des Flüssigkeitsspiegels über dem betrachteten Punkt

$p_{0}$ = Luftdruck auf Flüssigkeitsoberfläche

= hydrostatischer Druck in Abhängigkeit von der Höhe des Flüssigkeitsspiegels.

Einheiten

Die Physikalischen Einheiten für den hydrostatischen Druck sind:

international die SI-Einheit

Pascal (Pa): 1 Pa = 1 N/m²;
zudem in Deutschland und Österreich die „gesetzliche Einheit“

Bar (bar): 1 bar = 100.000 Pa bzw. N/m² (= 100 kPa)

Zur Beschreibung des hydrostatischen Drucks wird zum Teil auch noch die nicht-SI-konforme veraltete Maßeinheit Meter Wassersäule (mWS) verwendet.

Beispiel zum Hydrostatischen Paradoxon

Wassersäule, homogene Wassertemperatur: 3,98 °C, Höhe: 50 Meter:

1.000 kg/m³ × 9,81 m/s² × 50 m ≈ 490.500 N/m² ≈ 4,90 bar

Bei einer Temperatur von 20 °C hat Wasser eine Dichte von 998,203 kg/m³. Der hydrostatische Druck verändert sich minimal zu

998,203 kg/m³ × 9,81 m/s² × 50 m ≈ 489.618,57 N/m² ≈ 4,90 bar

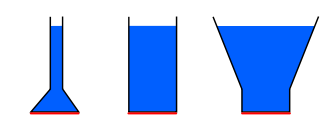
Der hydrostatische Druck hängt nicht von der Form eines Gefäßes ab; entscheidend für den Druck an dessen Boden ist alleine die Höhe des Fluid- bzw. Flüssigkeitsspiegels und dessen Dichte (in Abhängigkeit von der Temperatur), jedoch nicht die absolute Menge des Fluids im Gefäß. Dieses Phänomen wurde als Hydrostatisches (oder auch Pascal’sches) Paradoxon bekannt.

Gesamtdruck (Absolutdruck) am Boden der Flüssigkeit

Zur vollständigen Beschreibung des Drucks am Boden eines ruhenden inkompressiblen Fluids ist dem hydrostatischen Druck hinzu allerdings noch der Umgebungsdruck zu addieren. So entspricht beispielsweise der auf einen Taucher wirkende Wasserdruck in einem ruhenden Gewässer der Summe

aus dem Luftdruck, der auf die Gewässeroberfläche wirkt plus dem hydrostatischen Druck des Wassers selbst.

Beispiele

Für Taucher ist es wichtig zu wissen, welchem Druck ihre Körpergase (Stickstoff) ausgesetzt sind, um die Taucherkrankheit zu vermeiden.
Ein Bathyscaph muss einem besonders hohen hydrostatischen Druck standhalten.
Wassertürme nutzen den hydrostatischen Druck, um den für die Versorgung der Endverbraucher notwendigen Leitungsdruck zu erzeugen.
In der Hydrogeologie kann sich nach dem Darcy-Gesetz eine Strömung zwischen zwei Punkten nur dann einstellen, wenn die Druckdifferenz verschieden von der Differenz der hydrostatischen Drücke an den beiden Punkten ist.
Ein Heber ist ein Gerät oder eine Einrichtung, mit der man eine Flüssigkeit aus einem Behälter über den Behälterrand in einen tiefer gelegenen Behälter umfüllen oder ins Freie entleeren kann, ohne den Behälter umzukippen und ohne dass er ein Loch oder einen Auslass unter dem Flüssigkeitsspiegel hat.

Kontinuumsmechanik

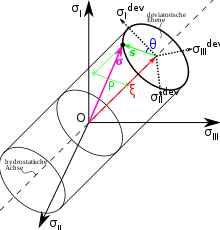
Die hydrostatische Achse im Haight-Westergaard Koordinatensystem ist in 3D das ${\sqrt {3}}$ -fache der mittleren Spannung: $\xi =-{\sqrt {3}}\,p$

In jeden Punkt (egal ob in einem Fluid, einem Festkörper oder im Vakuum) existiert ein Spannungstensor

${\boldsymbol {\sigma }}={\begin{pmatrix}\sigma _{11}&\sigma _{12}&\sigma _{13}\\\sigma _{21}&\sigma _{22}&\sigma _{23}\\\sigma _{31}&\sigma _{32}&\sigma _{33}\end{pmatrix}}\,,$

dieser besteht aus einem hydrostatischen Anteil

${\boldsymbol {\sigma }}_{\mathrm {hydro} }=-p\,{\boldsymbol {I}}={\begin{pmatrix}-p&0&0\\0&-p&0\\0&0&-p\end{pmatrix}}\,,$

mit dem hydrostatischen Druck $p={\frac {\sigma _{11}+\sigma _{22}+\sigma _{33}}{3}}$ und einem deviatorischen Anteil ${\boldsymbol {\sigma }}_{\mathrm {dev} }={\boldsymbol {\sigma }}-{\boldsymbol {\sigma }}_{\mathrm {hydro} }$ .

Bei isotropen (=richtungsunabhängien) Materialien wird die Versagensfläche üblicherweise in Abhängigkeit vom hydrostatischen und deviatorischen Anteil angegeben (beispielsweise die Mises-Spannung oder das Drucker-Prager Versagenskriterium), oftmals wird dazu das Haight-Westergaard Koordinatensystem verwendet, dort stellt die hydrostatische Achse eine Linie dar, und orthonal dazu spannt die deviatische Ebene den dreidimensionalen Hauptspannungsraum auf.

Gravitationsdruck in Planeten, Monden, Asteroiden und Meteoriten

Tiefenabhängigkeit von g

Mit zunehmender Tiefe kann nicht mehr als konstant betrachtet werden. Wenn die Form des Himmelskörpers durch eine Kugel mit Radius beschrieben und die Dichte als konstant betrachtet wird, lässt sich der Druck wie folgt berechnen:

$p(h)=\int _{0}^{h}\rho \,g(R-r)\,\mathrm {d} r$ .

Der Ortsfaktor g(r) folgt aus dem Newtonschen Gravitationsgesetz:

$g(r)=G{\frac {M(r)}{r^{2}}}=G{\frac {Mr}{R^{3}}}=\rho r{\frac {4\pi G}{3}}$ ,

wobei M(r) die Masse innerhalb einer konzentrischen Kugel innerhalb des Himmelskörpers und M=M(R) dessen Gesamtmasse angibt. Mit der Formel für das Kugelvolumen $V={\tfrac {4}{3}}\pi R^{3}$ ergibt sich für den Druck im Zentrum:

$p_{\text{Z}}=p(R)={\frac {3G}{8\pi }}{\frac {M^{2}}{R^{4}}}=\rho ^{2}R^{2}{\frac {2\pi G}{3}}$ .

Gravitationsdruck in Sternen

Sterne im Gleichgewicht

Einen Spezialfall des hydrostatischen Drucks stellt der Gravitationsdruck in Sternen dar. Dieser resultiert aus der den Stern kontrahierenden Schwerkraft. Demgegenüber wirkt z.B. der Strahlungsdruck als den Stern expandierende Kraft. Bei einem stabilen Stern stellt sich dabei ein Gleichgewicht aller Kräfte ein und der Stern hat eine stabile Form. Dies ist näherungsweise der Zustand von Sternen auf der Hauptreihe des Hertzsprung-Russell-Diagramms.

Beispiele für Sterne im Ungleichgewicht

Bei entstehenden Sternen, die sich zusammenziehen, überwiegt der Gravitationsdruck gegenüber der Summe aller Kräfte, die Gegendruck aufbauen. Beispiele für Gegendruck sind der kinetische Gasdruck des Gases selbst und bei anlaufender Fusionsreaktion der Strahlungsdruck durch alle auftretenden Strahlungsarten. Dadurch verändert sich der hydrostatische Druck innerhalb des entstehenden Sterns.

Bei einigen Klassen veränderlicher Sterne treten periodische oder transiente Änderungen der Sterndichte auf, wodurch sich die Materiemenge des Sterns, die innerhalb oder außerhalb einer Sphäre mit einem festen Radius liegt, verändert, und mit ihr auch der hydrostatische Druck bei einem bestimmten Radius vom Sternmittelpunkt aus.

Aufgrund des Sternwindes verlieren Sterne stetig Masse an die Umgebung. Auch dadurch ändert sich der hydrostatische Druck. Bei Hauptreihensternen ist diese Änderung allerdings sehr langsam.

In den Spätstadien des Sternenlebens kommt es ebenfalls zu Veränderungen im Sternaufbau, die sich auf den hydrostatischen Druck im Stern auswirken.

Basierend auf einem Artikel in:

Wikipedia.de