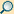Corioliskraft
Die Corioliskraft [kɔrjoˈliːskraft] ist eine Schein- oder Trägheitskraft, die einen bewegten Körper quer zu seiner Bewegungsrichtung ablenkt, wenn die Bewegung relativ zu einem rotierenden Bezugssystem beschrieben wird. Die Corioliskraft tritt nicht in Erscheinung, wenn die Bewegung aus Sicht eines nicht rotierenden Bezugssystems (z.B. eines Inertialsystems) beschrieben wird. Sie wurde 1775 von Pierre-Simon Laplace erstmals korrekt aus den Newton’schen Gesetzen der Mechanik hergeleitet, wird aber nach Gaspard Gustave de Coriolis benannt, der diese Kraft in einer 1835 erschienenen Publikation ausdrücklich hervorhob. Im Unterschied zu zwei anderen Scheinkräften in rotierenden Bezugssystemen, Zentrifugalkraft und Eulerkraft, wirkt die Corioliskraft nur auf Körper, die sich relativ zum rotierenden Bezugssystem (z.B. relativ zur Erdoberfläche oder zu einem Platz auf einem Karussell) bewegen. Zudem darf diese Bewegung nicht parallel zur Drehachse verlaufen. Allgemein wirkt die Corioliskraft bei Bewegungen in allen Richtungen, die zumindest eine Komponente senkrecht zur Drehachse haben, und verursacht ständig eine Ablenkung zu einer Seite, denn diese Kraft steht immer senkrecht zur augenblicklichen Bewegungsrichtung im rotierenden Bezugssystem. Im Fall der Bewegung in einer Ebene senkrecht zur Drehachse liegt auch die Corioliskraft in dieser Ebene und hat eine von der Bewegungsrichtung unabhängige Stärke. Daher wird jede Bewegung, die konstante Geschwindigkeit hat, zu einer Kreisbahn gekrümmt.
Spürbar ist die Corioliskraft z.B., wenn man auf einer Drehscheibe auf einem Kinderspielplatz zu laufen beginnt. Deutlich erkennbar wird der Einfluss der Corioliskraft auch bei langfristigen großräumigen Phänomenen, wie z.B. in der Meteorologie bei der Drehrichtung der Windfelder um Hoch- und Tiefdruckgebiete und bei der Ausbildung erdumspannender Windsysteme wie der Passatwinde und des Jetstreams. In der physikalischen Ozeanographie beeinflusst die Corioliskraft maßgeblich die Meeresströmungen. Die verbreitete These, dass sie auch für die Drehrichtung des Strudels in der Badewanne und im Spülbecken verantwortlich sei, trifft hingegen nicht zu. Wie stark der Einfluss der Corioliskraft auf die Strömung eines Mediums ist, wird durch deren Rossby-Zahl beschrieben.
Die Corioliskraft
und die dazugehörige Coriolis-Beschleunigung
berechnen sich nach den Formeln
und
.
Darin ist
die Winkelgeschwindigkeit
des Bezugssystems,
die Geschwindigkeit des Körpers relativ zu diesem Bezugssystem und
die Masse des Körpers. Die Corioliskraft ist das Kreuzprodukt
eines polaren Vektors mit einem
axialen Vektor und daher, wie alle Kräfte, ein polarer Vektor.
In der Technischen
Mechanik wird als Coriolisbeschleunigung diejenige Beschleunigung
bezeichnet, die das seitliche Abweichen des bewegten Körpers verhindert. Sie ist
das Negative der oben beschriebenen Coriolisbeschleunigung .
Einführung
Beobachtungen auf einer sich drehenden Scheibe
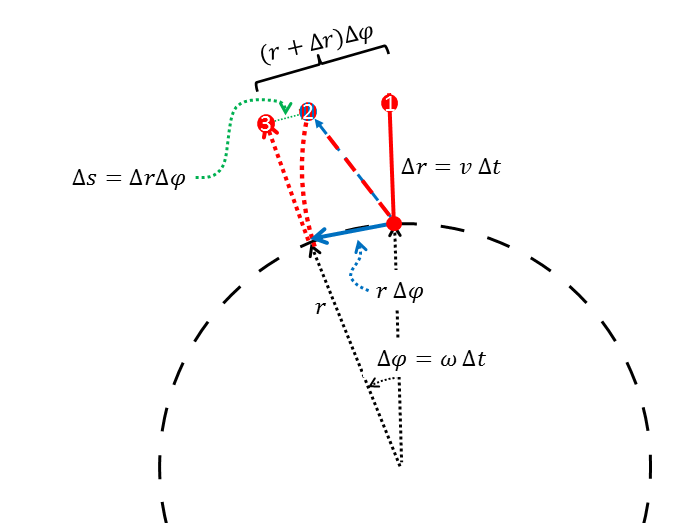
Fährt eine Person auf einer Drehscheibe (wie z.B. auf manchen Spielplätzen oder auf einem Karussell) einfach nur mit, so wirkt eine nach außen gerichtete Zentrifugalkraft auf sie. Bewegt sich die Person aber auch noch relativ zu der Scheibe, so erfährt sie außerdem eine Kraft, die sie aus ihrer momentanen Bewegungsrichtung zur Seite ablenkt. Dies ist die Corioliskraft. Ohne einige Übung macht sie das einfache Geradeausgehen zunächst praktisch unmöglich, wenn das „Geradeausgehen“ in Bezug auf die rotierende Scheibe gemeint ist. Besonders deutlich bemerkt man diese Kraft, wenn man von der Drehachse weg oder zu ihr hin gehen will. In diesem Fall steht die Corioliskraft senkrecht auf der Zentrifugalkraft und ist leicht von ihr zu unterscheiden. Aber auch, wenn man sich auf der Scheibe in beliebiger anderer Richtung bewegt, zieht die Corioliskraft mit gleicher Stärke zur Seite. In diesem Fall hat sie eine Komponente in Richtung der Zentrifugalkraft und ist von dieser nicht mehr so einfach zu unterscheiden. Dreht sich die Scheibe von oben gesehen linksherum, zieht die Corioliskraft seitlich nach rechts, immer bezogen auf die augenblickliche Richtung der Bewegung relativ zur Scheibe. Die folgenden Überlegungen, die dieses Phänomen anhand endlicher Intervalle in Zeit und Raum näherungsweise verständlich machen, ergeben im Grenzfall infinitesimal kleiner Intervalle eine exakte Begründung der Corioliskraft.
Coriolisbeschleunigung bei radialer Bewegung von der Achse weg
Wenn dem mit der Scheibe rotierenden Körper (roter Kreis in der
nebenstehenden Abbildung) zusätzlich eine Radialgeschwindigkeit
erteilt wird, wächst sein Abstand zur Achse in der Zeit
um
.
Im Bezugsystem der Scheibe würde er bei geradliniger Bewegung (also ohne
Corioliskraft) am Ende des durchgezogenen roten Pfeils an der Position 1
ankommen. Im erdfesten Bezugssystem bewegt sich der Körper entlang des Pfeils,
der die Vektorsumme der Radialbewegung und der Tangentialbewegung um die
Strecken
(roter Pfeil) bzw.
(blauer durchgezogener Pfeil) darstellt, zum blauroten Punkt mit der
Markierung 2. Jedoch dreht sich in dieser Zeit die Scheibe um den Winkel
,
und dabei hat der auf der Scheibe erwartete Endpunkt (Markierung 1) eine
größere Strecke zurückgelegt, nämlich insgesamt
bis zum roten Punkt mit der Markierung 3. Demnach ist der Körper in
tangentialer Richtung von der geradlinigen radialen Bahn auf der Scheibe nach
rechts abgewichen. Die mit
bezeichnete Abweichung ergibt sich aus der Skizze zu
.
Wegen
wächst
quadratisch mit der Zeit
,
entspricht also einer gleichmäßig
beschleunigten Bewegung mit der Coriolisbeschleunigung
.
Coriolisbeschleunigung bei Kreisbewegung um die Drehachse herum
Die nebenstehende Abbildung zeigt, dass ganz allgemein zur Beibehaltung einer
Kreisbewegung (rot) mit der Geschwindigkeit
eine Beschleunigung
quer zur geradlinigen Trägheitsbewegung erfolgen muss, in der Fachliteratur als
Zentripetalbeschleunigung bezeichnet. Während des
Zeitintervalls
muss sie eine radiale Bewegung um die Strecke
bewirken (grün). Diese ergibt sich aus dem gezeigten rechtwinkligen Dreieck,
wenn man zum Grenzfall infinitesimaler Intervalle übergeht, zu
.
Die quadratische Abhängigkeit von der Zeitspanne zeigt, dass eine konstante Beschleunigung
vorliegt.
Dies Ergebnis kann man auf drei verschiedene Weisen auswerten, je nach der
Bedeutung, die man den Größen
und
gibt. Im ersten Fall sei
die Bahngeschwindigkeit eines mitfahrenden Körpers ohne Bewegung relativ zur
Scheibe:
.
Dann ist
die Drehgeschwindigkeit der Scheibe, und es ergibt sich
.
Das ist die Zentripetalbeschleunigung,
die bei allen Kreisbewegungen auftritt und die durch eine Kraft bewirkt wird,
die die im rotierenden Bezugssystem herrschende Zentrifugalkraft
neutralisiert (denn in diesem ersten Fall ruht der Körper relativ zur Scheibe).
Im zweiten Fall sei
die Geschwindigkeit, mit der der Körper relativ zu der Drehscheibe auf einem
Kreis um die Achse läuft, so dass sich im rotierenden Bezugssystem eine
Kreisbewegung mit Bahngeschwindigkeit
zeigt. Dann ergibt sich aus der obigen Formel
,
das ist im Bezugssystem der Scheibe die zu dieser Kreisbewegung gehörige
Zentripetalbeschleunigung. Im dritten Fall wählt man
,
das ist die Geschwindigkeit, die der Körper aus dem zweiten Fall im ruhenden
Bezugssystem hat. Dann ergibt sich nach obiger Gleichung:
Umformung gemäß
und
ergibt für die wirkende Radialbeschleunigung:
Dies ist die Zentripetalbeschleunigung, die im ruhenden Bezugssystem zur betrachteten Bewegung gehört. Gleich groß, nur umgekehrt gerichtet, ist die Beschleunigung, die ein ansonsten kräftefreier Körper im Bezugssystem der Drehscheibe erfährt, wenn er sich darin tangential bewegt. Die Formel zeigt, dass diese radial gerichtete Beschleunigung nicht einfach die Summe aus den beiden Zentrifugalbeschleunigungen der beiden Kreisbewegungen mit bzw. auf der Drehscheibe ist, sondern einen dritten Summanden hat, nämlich die Coriolisbeschleunigung.
Keine Coriolisbeschleunigung bei Bewegung parallel zur Drehachse
Eine Bewegung parallel zur Rotationsachse, also senkrecht zur Drehscheibe, ruft keine Corioliskraft hervor. Beim senkrechten Hochhüpfen oder beim Hochschießen eines Gegenstandes parallel zur Drehachse ist jedoch zu beachten, dass er dann im Allgemeinen den mechanischen Kontakt zur Drehscheibe verliert, sodass diese keine Zentripetalkraft mehr auf ihn ausüben kann. Der Körper wird dann im Bezugssystem der Scheibe durch die horizontal wirkende Zentrifugalkraft beschleunigt und beginnt sich nach außen zu bewegen. Dadurch erhält er eine Geschwindigkeitskomponente senkrecht zur Drehachse und somit auch eine Corioliskraft. Der Körper wird dann (in Bezug auf die Drehscheibe) durch die vektorielle Summe aus Zentrifugalkraft und Corioliskraft weiter beschleunigt. Wenn der Körper wieder landet, z.B., weil eine Gravitationskraft (parallel zur Rotationsachse) ihn wieder herunter zieht, kommt er nicht mehr am Ausgangspunkt an.
Kinematische Herleitung
Für die Herleitung der Corioliskraft betrachte man ein Bezugssystem ,
das sich in einem Inertialsystem
befindet. Der Ursprung des Systems
sei frei im System
bewegbar, beschrieben durch die Vektoren für Position
,
Geschwindigkeit
und Beschleunigung
.
Eine zusätzliche Rotation ist durch die Winkelgeschwindigkeit
bzw. die Winkelbeschleunigung
gegeben. In diesem System
betrachten wir einen Punkt
mit Position
,
Geschwindigkeit
und Beschleunigung
.
Da sich
bezüglich
bewegt, ändern sich die Basisvektoren von
betrachtet aus
mit der Zeit. Es lässt sich zeigen, dass für die zeitliche Ableitung eines
Vektors
aus
gilt
wobei die partielle Ableitung hier die zeitliche Änderung in System
beschreibt.
Für den Vektor
vom Ursprung des Ineratialsystems zum Punkt
gilt
Die Geschwindigkeit entspricht der zeitlichen Ableitung des Ortes
Für die Beschleunigung folgt analog
Diese Gleichung stellt man nun nach der im rotierenden System
erfahrenen Beschleunigung
um.
In dieser Formel finden sich alle Trägheitsbeschleunigungen
im beschleunigten Bezugssystem wieder. Der letzte Term ist hierbei die
Coriolisbeschleunigung .
Wenn man angelehnt an das zweite
Newtonsche Gesetz annimmt, dass diese Beschleunigung durch eine zur Masse
proportionale Kraft bewirkt wird, erhält man die Corioliskraft :
Corioliskraft aufgrund der Erdrotation
Auf ein sich auf der Erde bewegendes Objekt wirkt die Corioliskraft, die auf die Erdrotation zurückgeht. Ausgenommen sind lediglich Bewegungen parallel zur Erdachse, z.B. an den Polen die vertikalen Bewegungen nach oben oder nach unten, am Äquator die horizontalen Bewegungen genau nach Norden oder nach Süden.
Vertikale Bewegungen
Außer an den Polen haben vertikale Bewegungen auf der Erdoberfläche einen senkrecht zur Erdachse gerichteten Anteil. Dieser erzeugt eine Corioliskraft, die bei einer Abwärtsbewegung nach Osten, bei einer Aufwärtsbewegung nach Westen gerichtet ist.
Lässt man einen Gegenstand fallen, wird er aufgrund der Corioliskraft nach Osten abgelenkt. Frühe Messungen dieses Effektes stammen von Giovanni Battista Guglielmini (1791 in Bologna), Johann Friedrich Benzenberg (1802 in Hamburg) und Ferdinand Reich (1832 in Freiberg).
Eine alte Frage, über die schon im 17. Jhdt. Marin Mersenne spekulierte, ist die, wo eine senkrecht nach oben geschossene Kanonenkugel wieder am Boden ankommt – ohne Berücksichtigung von Luftbewegung und Luftwiderstand. Durch die Corioliskraft wird die Kugel während der Aufwärtsbewegung nach Westen und während der Abwärtsbewegung nach Osten beschleunigt. Dadurch entsteht beim Aufstieg eine westliche Geschwindigkeitskomponente, die im Umkehrpunkt ihr Maximum erreicht, und beim Abstieg wegen der ostwärts gerichteten Corioliskraft gleichermaßen wieder abnimmt. Unten erreicht sie wieder den Wert Null. So hat während des gesamten Fluges die Geschwindigkeit eine nach Westen gerichtete Komponente. Im Ergebnis wird die Kugel daher nach Westen abgelenkt. Bei 50° geographischer Breite beträgt bei einer Anfangsgeschwindigkeit von 100 m/s (Steighöhe ca. 500 m) die Westablenkung 65 cm.
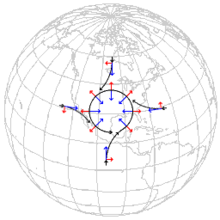
Rot – horizontale Komponente der Corioliskraft
Blau – Druckgradientkraft
Horizontale Bewegungen
Bei einer horizontalen Bewegung auf der Erdoberfläche hat die Corioliskraft im Allgemeinen eine Horizontal- und eine Vertikalkomponente. Die Horizontalkomponente zieht einen horizontal bewegten Körper auf der Nordhalbkugel aus der Bewegungsrichtung nach rechts, auf der Südhalbkugel nach links, und verschwindet am Äquator. Sie wirkt umso stärker, je schneller der Körper sich bewegt, und je näher er dem Nord- oder Südpol ist. Ihre Stärke ist aber unabhängig von der Richtung, in der der Körper sich horizontal bewegt. Daher werden geradlinige Bewegungen auf der Erdoberfläche zu Kreisen, und die Drehung des Foucaultschen Pendels erfolgt mit konstanter Winkelgeschwindigkeit. Die horizontale Corioliskraft hat wesentlichen Einfluss auf die Formen der großräumigen Bewegungen in der Atmosphäre und im Ozean. Theoretisch berücksichtigt wurde dies erstmals in der von Laplace (1778) aufgestellten Gezeitentheorie. Des Weiteren modifiziert die Corioliskraft den Wind und seinen Einfluss auf die Meeresströmungen, wie um 1905 von Vagn Walfrid Ekman erklärt wurde. Allgemein wird der Einfluss der Corioliskraft auf bestimmte Bewegungen etwa im Meer und in der Atmosphäre durch die dimensionslose Rossby-Zahl charakterisiert. Je kleiner diese ist, umso stärker ist die Bewegung durch Corioliskraft geprägt.
Die Vertikalkomponente der Corioliskraft ist neben der Schwerkraft, die parallel zu ihr wirkt, meist vernachlässigbar schwach und spielt in der Praxis nur als Korrekturglied bei Präzisionsmessungen des Erdschwerefeldes eine Rolle. Sie verschwindet an den Polen, und ist maximal am Äquator. Sie macht z.B. ein Flugzeug, das dort mit Schallgeschwindigkeit nach Osten fliegt, um annähernd ein Tausendstel seines Gewichts leichter – fliegt es nach Westen, wird es entsprechend schwerer. In der Geophysik, z.B. in Bezug zu rein horizontalen Ozean- oder Luftströmungen, bezeichnet man daher meist die horizontale Komponente der vollen Corioliskraft allein schon als „die Corioliskraft“. Für sie gilt, wie für das oben erläuterte Beispiel der horizontalen Drehscheibe, dass die Corioliskraft stets quer zur Bewegungsrichtung wirkt und dass ihre Stärke nicht von der Bewegungsrichtung abhängt.
Einfluss der Corioliskraft auf das Wetter

Die Corioliskraft ist dafür verantwortlich, dass großräumig betrachtet die Luftmassen von Hochdruckgebieten nicht einfach zu Tiefdruckgebieten strömen, wie es das Druckgefälle nahelegt, sondern Spiralbahnen beschreiben. Allgemein dreht sich die Luft auf der Nordhalbkugel um Hochdruckgebiete im Uhrzeigersinn, um Tiefdruckgebiete gegen den Uhrzeigersinn. Auf der Südhalbkugel ist dies genau umgekehrt. Diese Wirbel entstehen dadurch, dass die vom Druckgefälle vom Hochdruckgebiet zum Tiefdruckgebiet hin beschleunigte Luft durch die Corioliskraft abgelenkt wird, auf der Nordhalbkugel nach rechts. Die Luft verlässt das Hochdruckgebiet daher in Form eines rechts drehenden Wirbels, also im Uhrzeigersinn. Um das Tiefdruckgebiet entsteht aus dem gleichen Grund ein linksdrehender Wirbel. Die dort hineinströmende Luft wird nach rechts abgelenkt und kann sich dem Zentrum nur in dem Maß nähern, in dem das Druckgefälle eine Linkskurve verursacht. Das sich ergebende Strömungsbild lässt sich durch das geostrophische Gleichgewicht zwischen dem horizontalen Druckgefälle und der Corioliskraft erklären: In einem Wirbel, der sich um ein Tiefdruckgebiet gegen den Uhrzeigersinn dreht, wirkt die Corioliskraft nach außen und kompensiert die nach innen gerichtete Kraft, die vom Druckgefälle verursacht ist. Das geostrophische Gleichgewicht formt nur die großskaligen Wettermuster. Auf die Drehrichtung im kleinräumigen Bereich, beispielsweise von Tornados hat die Corioliskraft keinen direkten Einfluss. Weiterhin spielt die Corioliskraft auch bei der Bildung der Rossbywellen und der verschiedenen äquatorialen Wellen eine wichtige Rolle.
Corioliskraft und Eisenbahn
Im Schienenverkehr führt die Corioliskraft theoretisch dazu, dass bei geraden Strecken diejenige Schiene, die in Fahrtrichtung rechts liegt, auf der Nordhalbkugel geringfügig stärker belastet wird als die linke Schiene. Dieser Effekt ist aber so klein, dass er gegenüber geringfügigen Krümmungen und Höhenunterschieden beider Schienen, die ebenfalls eine ungleichmäßige Belastung zur Folge haben, keine technische Relevanz hat.
Ein Zug (z.B. ein ICE 3 mit 400 t Masse), der bei einer geografischen Breite von 51 Grad (Köln) mit einer Geschwindigkeit von 250 km/h fährt, erfährt eine Corioliskraft von 3.200 N nach rechts. Dies ist weniger als ein Promille der Gewichtskraft. Hat der Zug acht Wagen mit je vier Achsen, wird jedes rechte Rad mit einer Corioliskraft von ca. 100 N nach rechts gegen die Schiene gedrückt. Im Vergleich dazu ergibt sich bei dieser Geschwindigkeit und bei einem Kurvenradius von 3.000 m die zur Kurvenfahrt erforderliche Zentripetalkraft auf jedes Rad zu 20.000 N, also 200-mal so viel wie die Corioliskraft.
Trägheitskreise
Da die horizontale Corioliskraft von der Himmelsrichtung einer horizontalen
Bewegung unabhängig ist, beschreibt eine Luft- oder Wassermasse, in einem
mitrotierenden Bezugssystem mit der horizontalen Geschwindigkeit
bewegt, ohne Einfluss anderer Kräfte „Trägheitskreise“ mit Radien von
In mittleren Breiten mit Werten des Coriolisparameters (siehe unten) von
und einer typischen Meeres-Strömungsgeschwindigkeit von
ergibt sich ein Radius von
Die Bewegung erfolgt auf der Nordhalbkugel im Uhrzeigersinn, auf der
Südhalbkugel entgegen dem Uhrzeigersinn. Die Periode der Umlaufbewegung ist
z.B. bei 60 Grad geographischer Breite rund 15 Stunden. Sie
wurden z.B. bei frei schwimmenden Bojen in der Ostsee beobachtet, die
zunächst einer durch starke Winde angefachten Oberflächenströmung folgten, nach
dem Abflauen des Windes aber Kreisbahnen bzw. Zykloiden
(da eine Strömung der Kreisbewegung überlagert war) beschrieben.
Für den Verlauf von Meeres- und Luftströmungen spielt die Corioliskraft eine
wichtige Rolle, neben anderen Kräften, die sich mit ihr ins Gleichgewicht setzen
oder sie sogar dominieren (Geostrophie).
Corioliskraft und Foucaultsches Pendel
Der Begriff der Corioliskraft erlaubt ein einfaches Verständnis des Foucaultschen Pendels. Da das Pendel (auf der Nordhalbkugel) durch die Corioliskraft ständig nach rechts gezogen wird, dreht sich seine Schwingungsebene. Die Geschwindigkeit dieser Drehung ist am Pol genau 1 Umdrehung pro Tag und nimmt mit dem Sinus der geografischen Breite zum Äquator hin auf Null ab.
Erosion von Flussufern
Die Corioliskraft führt auch dazu, dass auf der Nordhalbkugel diejenigen Flussufer, die in Fließrichtung rechts liegen, im Mittel stärker erodiert werden als die linken. Dieses Phänomen wurde erstmals im Jahre 1763 von Michail Wassiljewitsch Lomonossow beschrieben. Erste Erklärungen stammten von Pjotr Andrejewitsch Slowzow (1827) und Karl Ernst von Baer (1856). Obwohl diese Forscher glaubten, der Effekt trete nur bei Flüssen auf, die von Süden nach Norden fließen, wird der Effekt bis heute als Baersches Gesetz bezeichnet. Die korrekte Sichtweise, dass der Effekt von der Fließrichtung unabhängig ist, formulierte 1859 erstmals Jacques Babinet und später Albert Einstein (1926).
Corioliskraft in der Technik
Corioliskräfte sind in der Technik dann von Bedeutung, wenn eine Drehbewegung von einer zweiten Bewegung „überlagert“ wird. Dies ist beispielsweise bei einem Roboter der Fall, der sich dreht und gleichzeitig seinen Greifarm ausfährt.
- Wenn eine Last am Ausleger eines Krans nach innen oder außen fährt, während der Kran sich dreht, hängt sie aufgrund der Corioliskraft nicht senkrecht nach unten, sondern wird seitlich ausgelenkt. Wird die Last längs des Auslegers nach innen eingefahren, eilt sie der Drehung des Krans voraus.
- In der Getriebetechnik (Koppelgetriebe) und in der Robotik spielen die Corioliskräfte ebenfalls eine wichtige Rolle, da auch hier gleichzeitige Bewegungen entlang mehrerer Freiheitsgrade erfolgen. Benutzt man zur Vereinfachung der Beschreibung rotierende Koordinatensysteme, treten für Bewegungen in diesen rotierenden Bezugssystemen auch Corioliskräfte auf.
- Zur Messung des Massenstromes durchströmender Flüssigkeiten oder Gase verwendet man den Coriolis-Massendurchflussmesser. Das Messrohr wird in Schwingungen versetzt. Diese werden im Ein- und Auslauf gemessen und verglichen. Bei der Corioliswaage wird vor allem Schüttgut durch die Messung der Änderung des benötigten Drehmoments eines Rotortellers vermessen.
- Bei Kreiselpumpen wird das Medium vom meist axial gelegenen Ansaugkanal durch das Pumpenrad in Rotation versetzt und durch die Zentrifugalkraft nach außen zum Ausgang geschleudert. Dabei übt das Medium Corioliskräfte auf das Pumpenrad aus, wodurch sich ein Bremsmoment für den Antrieb ergibt. Die effektiv aufgewendete Energie der Pumpe ist also etwa proportional zum radial verlaufenden Massenstrom, dem Radius des Pumpenrades und der Drehzahl (Verwirbelungen, Rückströmungen und Reibung außer Acht gelassen).
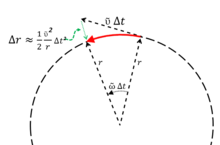
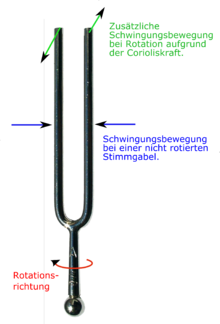
- Einige Drehratensensoren zur Messung von Drehgeschwindigkeiten nutzen die Corioliskraft in Form des sogenannten „Stimmgabelprinzips“, das im nebenstehenden Bild erläutert wird. Aufgrund der Drehbewegung bewegen sich die Zinken der Stimmgabel nicht nur aufeinander zu, sondern sie führen zusätzlich seitliche Bewegungen zueinander aus, die durch die Corioliskraft verursacht werden. Die seitliche Auslenkung ist näherungsweise proportional zur Drehgeschwindigkeit und kann beispielsweise durch eine kapazitive oder induktive Messung erfasst werden.
Berechnung und Spezialfälle
Die Coriolisbeschleunigung
und bei Körpern der Masse
auch die Corioliskraft
wirkt auf einen Körper, der sich in einem rotierenden Bezugssystem bewegt. Dafür
gilt allgemein die Formel
.
Bei bekanntem Winkel
zwischen Geschwindigkeit und Rotationsachse kann man mit den Beträgen rechnen:
.
Die Richtung der Kraft ist bei einem sich in mathematisch positiver Richtung,
also links herum, drehenden System in Bewegungsrichtung gesehen rechtwinklig
nach rechts, bei einem sich in mathematisch negativer Richtung drehenden System
rechtwinklig nach links. In den typischen Koordinatendarstellungen bei
rotierenden Systemen stellen sich die Formeln so dar:
| Zylinderkoordinaten | Kugelkoordinaten | geografische Koordinaten |
|---|---|---|
Dabei ist
der Betrag der Winkelgeschwindigkeit des Bezugssystems und
der Geschwindigkeitsvektor der Bewegung des Körpers, relativ zum rotierenden Bezugssystem, und dabei bezeichnen
- bei den Zylinderkoordinaten der Index
die Komponente parallel zur Rotationsachse
und die Indizes
und
die radiale und tangentiale Komponenten senkrecht zur Rotationsachse,
- bei den Kugelkoordinaten der Index
den Abstand zum Ursprung und die Indizes
und
den Azimut- und Polarwinkel,
- bei den geografischen Koordinaten der Index
den Abstand zur Kugeloberfläche und die Indizes
und
die geografische Breite und Länge.
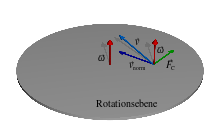
Überlagerung mit der Zentrifugalkraft bei tangentialer Bewegung
Steht man z.B. auf einer Drehscheibe, spürt man nur die Zentrifugalkraft und muss sie durch eine gleich große Zentripetalkraft ausgleichen. Läuft man aber in konstantem Abstand von der Achse entgegen der Drehbewegung, dann scheint sich die Zentrifugalkraft zu verringern, obwohl die Scheibe unverändert rotiert. Der Grund ist die zusätzlich wirkende Corioliskraft radial nach innen. Läuft man gerade mit der Umlaufgeschwindigkeit der Scheibe, ist die Corioliskraft genau doppelt so groß wie die Zentrifugalkraft. Als resultierende Kraft erfährt der Körper also genau die Kraft, die er benötigt, um sich – aus Sicht des rotierenden Bezugssystems – auf einer Kreisbahn entgegengesetzt der Rotationsgeschwindigkeit zu halten. Aus dem Inertialsystem heraus gesehen ruht der Körper und ist kräftefrei. Bewegt sich der Körper hingegen in Richtung der Rotation, wirkt die Corioliskraft nach außen – dadurch ist eine größere Zentripetalkraft notwendig als im nicht rotierenden System, um ihn auf seiner Bahn zu halten. Vom Betrag her ergibt sich die Gleichheit der Kräfte genau dann, wenn man die Corioliskraft mit berücksichtigt:
Bewegt sich der Körper in konstantem Abstand
zur Rotationsachse, mit der Geschwindigkeit
im rotierenden Bezugssystem, dann entspricht das im Inertialsystem einer
Kreisbewegung mit der Geschwindigkeit
.
Berechnet man nun die scheinbare Zentrifugalkraft aus dem Inertialsystem
und aus dem rotierenden System heraus
,
wird die Gleichheit der Beträge durch die Corioliskraft hergestellt:
Dabei gilt:
ist die Zentrifugalkraft, die aufgrund der Rotation des Bezugssystems auftritt, selbst wenn der Körper sich nicht bewegte. Diese ist nach außen gerichtet und proportional zum Quadrat der Winkelgeschwindigkeit und dem Abstand von der Rotationsachse.
ist die Zentrifugalkraft, die aufgrund der kreisförmigen Bewegung relativ zum Bezugssystem auftritt, selbst wenn das System nicht rotierte. Diese ist nach außen gerichtet und proportional zum Quadrat der Bewegungsgeschwindigkeit geteilt durch den Krümmungsradius der Bewegung.
ist die Corioliskraft. Sie ist nach außen gerichtet, wenn sich der Körper in Richtung der Rotation bewegt und nach innen, wenn er sich entgegen der Rotation bewegt.
Bewegung auf der Oberfläche einer Kugel und Coriolisparameter
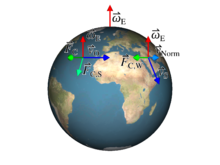
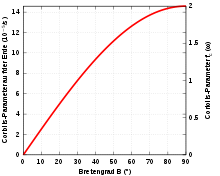
Bei horizontalen Bewegungen - also solchen, die auf die Oberfläche einer
Kugel eingeschränkt sind - fällt in geografischen Koordinaten
und die vertikale Komponente der Coriolisbeschleunigung
weg. Mit dem Coriolisparameter
ergibt sich dann der Betrag der horizontalen Komponente der
Coriolisbeschleunigung
als
und die Richtung so, dass
ein Rechtssystem bildet. Die Erdrotation (eine Umdrehung in 23 Stunden
56 Minuten 4,09 Sekunden = 1 Sternentag
= 86164,09 s) erfolgt mit einer Winkelgeschwindigkeit von
Damit nimmt der Coriolisparameter in mittleren Breiten eine typische
Größenordnung von
an.
Vertikale Bewegung – Das Gedankenexperiment von Mersenne
Bei reinen Aufwärtsbewegungen wirkt die Corioliskraft nach Westen, beim senkrechten freien Fall wirkt sie nach Osten. Ihr Betrag ist
Ein über die Länge
frei fallender Körper erfährt aufgrund der Corioliskraft eine Ostablenkung von
Eine mit der Anfangsgeschwindigkeit
senkrecht nach oben geschossene Kugel wird zunächst nach Westen abgelenkt um den
Betrag
Hat sie die Steighöhe
erreicht, so besitzt sie eine Westgeschwindigkeit von
Beim Herunterfallen der Kugel muss man deshalb zusätzlich zur obigen Formel
noch den Beitrag
zur Ostablenkung berücksichtigen:
Der gesamte Versatz ergibt sich aus der Differenz der beiden Ausdrücke nach Vereinfachungen zufolge der Gesetze für die Steig- und Fallzeiten zu einer effektiven Abweichung nach Westen um
g ist dabei jeweils die Erdbeschleunigung.
Am Äquator ist der Versatz am größten ().
Wegen
ergibt sich kein Unterschied zwischen Nord- und Südhalbkugel.
Verwandte Begriffe
Als Corioliseffekt wird jede Erscheinung bezeichnet, die durch die Corioliskraft entsteht.
Experimenteller Zugang
Am Teufelsrad, das als Fahrgeschäft um 1910 aufkam und nur mehr an wenigen Orten betrieben wird, kann an der eigenen Körperbewegung die Corioliskraft erfahren werden. Ebenso am Drehhocker, wenn durch Heranziehen der Arme der Pirouetteneffekt ausgelöst wird. Hierbei wirkt die mit der Erhöhung der Winkelgeschwindigkeit verbundene Trägheitskraft allerdings der Corioliskraft entgegen und hebt sie im Extremfall eines kreisenden Massenpunktes sogar ganz auf.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 21.12. 2022