Strömungswiderstandskoeffizient

Physikalische Kennzahl

Name

Strömungswiderstandskoeffizient,
Widerstandsbeiwert

Formelzeichen

$c_\mathrm w$

Dimension

dimensionslos

Definition

$c_\mathrm w = \frac{F_\mathrm w}{q \cdot A}$

$F_\mathrm w$	Widerstandskraft
	Staudruck der Anströmung
	Referenzflächeninhalt

Anwendungsbereich

Luftwiderstand von Fahrzeugen

Der Strömungswiderstandskoeffizient, Widerstandsbeiwert oder c_w-Wert (nach dem üblichen Formelzeichen $c_{\mathrm w}$ ) ist ein dimensionsloses Maß (Koeffizient) für den Strömungswiderstand eines von einem Fluid umströmten Körpers. Er entspricht dem Druckverlustbeiwert eines durchströmten Körpers (z.B. eines Ventils).

Umgangssprachlich ausgedrückt ist der $c_\mathrm w$ -Wert ein Maß für die „Windschlüpfigkeit“ eines Körpers. Es lässt sich aus dem Strömungswiderstandskoeffizienten bei zusätzlicher Kenntnis von Geschwindigkeit, Stirnfläche und Dichte des Fluids (z.B. der Luft) die Kraft des Strömungswiderstands berechnen.

Definition

Der Strömungswiderstandskoeffizient ist durch:

$c_\mathrm w \,=\, \frac{F_\mathrm w}{q \, A} \,=\, \frac{2 F_\mathrm w}{\rho\, v^{\,2} A}$

definiert. Hierbei wird die Widerstandskraft $F_\mathrm w$ auf den Staudruck der Anströmung und eine Referenzfläche normiert. Ferner bilden $\rho$ die Dichte und die Geschwindigkeit der ungestörten Anströmung. Die Referenzfläche ist definitionsabhängig. Üblicherweise ist sie gleich der Stirnfläche des angeströmten Körpers. In der Flugzeugaerodynamik wird jedoch die Flügelfläche als Referenz herangezogen.

Andere Bezeichnungen für den Strömungswiderstandskoeffizient lauten (Luft-)Widerstandsbeiwert, -koeffizient oder Stirnwiderstand. Das Formelzeichen $c_\mathrm w$ (mit w für Widerstand) ist nur im deutschen Sprachraum üblich; im Englischen wird der Drag-Coefficient als $c_\mathrm d$ oder $c_\mathrm x$ notiert.

Widerstandsfläche

Das Produkt $c_\mathrm w \cdot A$ wird als Widerstandsfläche bezeichnet. Die Betrachtung von Widerstandsflächen ist beispielsweise für den Vergleich von Fahrzeugen im Originalmaßstab sinnvoll, weil in den Gesamtwiderstand eines angeströmten Körpers sowohl die Körperform als auch die Abmessungen eingehen.

Abhängigkeit des Strömungswiderstandskoeffizienten

Strömungswiderstandskoeffizient einer Kugel in Abhängigkeit von der Reynolds-Zahl c_w=f(Re). Die charakteristische Länge ist in diesem Fall der Kugeldurchmesser d; die Bezugsfläche A ist eine Kreisfläche mit dem Durchmesser d.

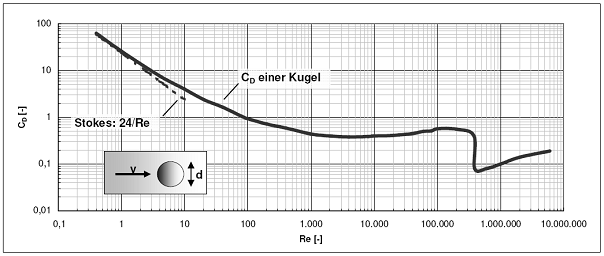
Allgemein gilt, dass bei inkompressibler Strömung^{[Anm.
1]} der Strömungswiderstandskoeffizient c_W von der Reynolds-Zahl $\mathit{Re}$ abhängt:

$c_\mathrm w = f(\mathit{Re}) \!\,$ mit $\mathit{Re} = \frac{v L \rho}{\eta}$

Diese Aussage ergibt sich, wenn man davon ausgeht, dass die Strömungswiderstandskraft $F_\mathrm w$ eines Körpers in einer bestimmten Lage abhängig von der Anströmgeschwindigkeit , der Dichte $\rho$ und der Viskosität (Zähigkeit) $\eta$ des Fluids sowie einer charakteristischen Länge des Körpers ist. Die charakteristische Länge ist eine bestimmte geometrische Abmessung, deren Quadrat L^2 in einem festen Verhältnis zur Bezugsfläche steht.

$F_\mathrm w = f(v,\,\rho,\,\eta,\,L)$

Mittels einer Dimensionsanalyse nach dem Buckinghamschen Π-Theorem lässt sich ableiten, dass die zwei Ähnlichkeitskennzahlen Strömungswiderstandskoeffizient $c_\mathrm w$ und Reynoldszahl $\mathit{Re}$ ausreichen, um den Strömungswiderstand eines bestimmten Körpers zu beschreiben, was eine unkompliziertere allgemeingültige Darstellung des Widerstandes einer bestimmten Körperform ermöglicht.

Stumpfe, kantige Körper haben über einen großen Bereich der Reynolds-Zahl einen weitgehend konstanten Widerstandsbeiwert. Das ist z.B. beim Luftwiderstand von Kraftfahrzeugen bei den relevanten Geschwindigkeiten der Fall.

c_w in Abhängigkeit von der Strömungsgeschwindigkeit

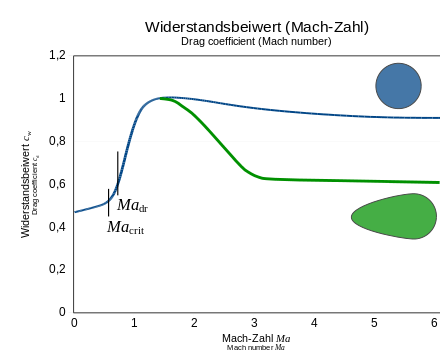
Bei kompressiblen Strömungen, also bei Strömungen mit veränderlicher Dichte, besteht auch eine Abhängigkeit des Strömungswiderstandskoeffizienten von der Mach-Zahl. Im transsonischen Bereich und im Überschallbereich ändert sich der Strömungswiderstandskoeffizient stark. In der Nähe der Schallgeschwindigkeit steigt er auf ein Mehrfaches an und sinkt bei sehr hohen Machzahlen auf etwa den doppelten Unterschall-c_w-Wert. Die Grafik veranschaulicht den Zusammenhang schematisch. Oberhalb der kritischen Machzahl überschreiten Teilumströmungen die Schallgeschwindigkeit. Oberhalb der Widerstandsdivergenzmachzahl steigt der Strömungswiderstand stark an. Das Verhalten im Überschallbereich wird bestimmt durch die Geometrie des Körpers. In der Zeichnung steht die grüne Kurve für einen stromlinienförmigen Körper.

Der Widerstandsbeiwert bestimmt für Satelliten ihre Lebensdauer im Orbit. Bei einer Flughöhe oberhalb von ca. 150 km ist die Atmosphäre so dünn, dass die Strömung nicht mehr als laminare Kontinuumsströmung, sondern als freie molekulare Strömung approximiert wird. In diesem Bereich liegt der c_w-Wert typischerweise zwischen 2 und 4, oft wird mit einem Wert von 2,2 gerechnet. Mit steigender Höhe verringert sich der Einfluss der Atmosphäre und ist oberhalb von ca. 1000 km vernachlässigbar.

Ermittlung

Der Strömungswiderstandskoeffizient wird üblicherweise im Windkanal ermittelt. Der Körper steht dabei auf einer Platte, die mit Kraftsensoren ausgestattet ist. Die Kraft in Richtung der Anströmung wird gemessen. Aus dieser Widerstandskraft $F_\mathrm w$ und den bekannten Größen wie Luftdichte und Stirnfläche wird der Strömungswiderstandskoeffizient bei gegebener Anströmgeschwindigkeit errechnet. Neben der experimentellen Ermittlung kann der Widerstand je nach Komplexität der Modellform und verfügbarer Rechnerkapazität auch numerisch über die Integration der Verteilung von Reibungs- und Druckbeiwert über die Modelloberfläche berechnet werden.

Anwendung

Aus dem Strömungswiderstandskoeffizienten wird die Widerstandskraft $F_\mathrm w$ wie folgt berechnet:

$F_\mathrm w = \frac{\rho\,c_\mathrm w\, A\,v^{\,2}}{2}$

Der Strömungswiderstand hängt somit ab von

der Dichte des strömenden Fluids $\rho$ (vergleiche Luftdichte!),
der Referenzfläche ,
der Strömungsgeschwindigkeit und
dem Strömungswiderstandskoeffizienten $c_\mathrm w$ .

Der Luftwiderstand ist somit jeweils proportional zum Strömungswiderstandskoeffizient, zur projizierten Frontfläche und zum Quadrat der Geschwindigkeit. Die erforderliche Antriebsleistung ist wegen $P = \vec F \cdot \vec v$ sogar proportional zur dritten Potenz der Geschwindigkeit. Daher hat die Wahl der Geschwindigkeit bei Kraftfahrzeugen neben den anderen beiden Faktoren besondere Auswirkung auf den Treibstoffverbrauch.

Der Luftwiderstand ist ausschlaggebend für die Abweichung der tatsächlichen ballistischen Kurve von der idealisierten Wurfparabel.

Beispiele

c_w-Werte von typischen Körperformen

Wert	Form
2,3	Halbrohr lang, konkave Seite
2,0	lange Rechteckplatte
1,33	Halbkugelschale, konkave Seite, Fallschirm
1,2	Halbrohr lang, konvexe Seite
1,2	langer Zylinder, Draht (Re < 1,9 · 10⁵)
1,11…1,17	runde Scheibe, quadratische Platte
0,78	Mensch, stehend
0,6	Gleitschirm (Bezugsfläche Strömungsquerschnittsfläche!)
0,53…0,69	Fahrrad (Mountainbike, gestreckt/aufrecht)
0,45	Kugel (Re < 1,7 · 10⁵)
0,4	Fahrrad (Rennrad)
0,35	langer Zylinder, Draht (Re > 6,7 · 10⁵)
0,34	Halbkugelschale, konvexe Seite
0,09…0,18	Kugel (Re > 4,1 · 10⁵)
0,08	Flugzeug (Bezugsfläche Tragfläche)
0,03	Pinguin
0,02	Tropfen stromlinienförmig

$\mathrm{Re}$ bezeichnet hierbei die Reynolds-Zahl

Anmerkungen

↑ Auch kompressible Fluide wie Luft können als inkompressibel betrachtet werden, wenn die Dichte im Strömungsfeld weitestgehend konstant ist. Das ist bis zu einer Mach-Zahl von 0,3 im Allgemeinen der Fall.

Basierend auf einem Artikel in:

Wikipedia.de

Strömungswiderstandskoeffizient

Definition

Widerstandsfläche

Abhängigkeit des Strömungswiderstandskoeffizienten

Ermittlung

Anwendung

Beispiele

cw-Werte von typischen Körperformen

Anmerkungen

c_w-Werte von typischen Körperformen