
Fermat-Zahl
Eine Fermat-Zahl, benannt nach dem französischen Mathematiker Pierre de Fermat, ist eine Zahl der Form
mit einer ganzen
Zahl .
Im August 1640 vermutete Fermat, dass alle Zahlen dieser Form (die später nach ihm benannt wurden) Primzahlen seien. Dies wurde jedoch 1732 von Leonhard Euler widerlegt, der zeigte, dass die sechste Fermatzahl F5 durch 641 teilbar ist. Man kennt außer den ersten fünf (3, 5, 17, 257, 65537) derzeit keine weitere Fermat-Zahl, die eine Primzahl ist, und vermutet, dass es außer diesen Zahlen auch keine weitere gibt.
Fermat-Zahlen
Die ersten Fermat-Zahlen lauten
und
.
Eine etwas längere Liste bis
findet man in der folgenden aufklappbaren Box.
| n | Dezimal- stellen von Fn |
Fn |
|---|---|---|
| 0 | 1 | 3 |
| 1 | 1 | 5 |
| 2 | 2 | 17 |
| 3 | 3 | 257 |
| 4 | 5 | 65.537 |
| 5 | 10 | 4.294.967.297 |
| 6 | 20 | 18.446.744.073.709.551.617 |
| 7 | 39 | 340.282.366.920.938.463.463.374.607.431.768.211.457 |
| 8 | 78 | 115.792.089.237.316.195.423.570.985.008.687.907.853.269.984.665.640.564.039.457.584.007.913.129.639.937 |
| 9 | 155 | 13.407.807.929.942.597.099.574.024.998.205.846.127.479.365.820.592.393.377.723.561.443.721.764.030.073.546.976.801.874.298.166.903.427.690.031.858.186.486.050.853.753.882.811.946.569.946.433.649.006.084.097 |
| 10 | 309 | 179.769.313.486.231.590.772.930.519.078.902.473.361.797.697.894.230.657.273.430.081.157.732.675.805.500.963.132.708.477.322.407.536.021.120.113.879.871.393.357.658.789.768.814.416.622.492.847.430.639.474.124.377.767.893.424.865.485.276.302.219.601.246.094.119.453.082.952.085.005.768.838.150.682.342.462.881.473.913.110.540.827.237.163.350.510.684.586.298.239.947.245.938.479.716.304.835.356.329.624.224.137.217 |
| 11 | 617 | 32.317.006.071.311.007.300.714.876.688.669.951.960.444.102.669.715.484.032.130.345.427.524.655.138.867.890.893.197.201.411.522.913.463.688.717.960.921.898.019.494.119.559.150.490.921.095.088.152.386.448.283.120.630.877.367.300.996.091.750.197.750.389.652.106.796.057.638.384.067.568.276.792.218.642.619.756.161.838.094.338.476.170.470.581.645.852.036.305.042.887.575.891.541.065.808.607.552.399.123.930.385.521.914.333.389.668.342.420.684.974.786.564.569.494.856.176.035.326.322.058.077.805.659.331.026.192.708.460.314.150.258.592.864.177.116.725.943.603.718.461.857.357.598.351.152.301.645.904.403.697.613.233.287.231.227.125.684.710.820.209.725.157.101.726.931.323.469.678.542.580.656.697.935.045.997.268.352.998.638.215.525.166.389.437.335.543.602.135.433.229.604.645.318.478.604.952.148.193.555.853.611.059.596.230.657 |
| 12 | 1234 | 1.044.388.881.413.152.506.691.752.710.716.624.382.579.964.249.047.383.780.384.233.483.283.953.907.971.557.456.848.826.811.934.997.558.340.890.106.714.439.262.837.987.573.438.185.793.607.263.236.087.851.365.277.945.956.976.543.709.998.340.361.590.134.383.718.314.428.070.011.855.946.226.376.318.839.397.712.745.672.334.684.344.586.617.496.807.908.705.803.704.071.284.048.740.118.609.114.467.977.783.598.029.006.686.938.976.881.787.785.946.905.630.190.260.940.599.579.453.432.823.469.303.026.696.443.059.025.015.972.399.867.714.215.541.693.835.559.885.291.486.318.237.914.434.496.734.087.811.872.639.496.475.100.189.041.349.008.417.061.675.093.668.333.850.551.032.972.088.269.550.769.983.616.369.411.933.015.213.796.825.837.188.091.833.656.751.221.318.492.846.368.125.550.225.998.300.412.344.784.862.595.674.492.194.617.023.806.505.913.245.610.825.731.835.380.087.608.622.102.834.270.197.698.202.313.169.017.678.006.675.195.485.079.921.636.419.370.285.375.124.784.014.907.159.135.459.982.790.513.399.611.551.794.271.106.831.134.090.584.272.884.279.791.554.849.782.954.323.534.517.065.223.269.061.394.905.987.693.002.122.963.395.687.782.878.948.440.616.007.412.945.674.919.823.050.571.642.377.154.816.321.380.631.045.902.916.136.926.708.342.856.440.730.447.899.971.901.781.465.763.473.223.850.267.253.059.899.795.996.090.799.469.201.774.624.817.718.449.867.455.659.250.178.329.070.473.119.433.165.550.807.568.221.846.571.746.373.296.884.912.819.520.317.457.002.440.926.616.910.874.148.385.078.411.929.804.522.981.857.338.977.648.103.126.085.903.001.302.413.467.189.726.673.216.491.511.131.602.920.781.738.033.436.090.243.804.708.340.403.154.190.337 |
| 13 | 2467 | 1.090.748.135.619.415.929.462.984.244.733.782.862.448.264.161.996.232.692.431.832.786.189.721.331.849.119.295.216.264.234.525.201.987.223.957.291.796.157.025.273.109.870.820.177.184.063.610.979.765.077.554.799.078.906.298.842.192.989.538.609.825.228.048.205.159.696.851.613.591.638.196.771.886.542.609.324.560.121.290.553.901.886.301.017.900.252.535.799.917.200.010.079.600.026.535.836.800.905.297.805.880.952.350.501.630.195.475.653.911.005.312.364.560.014.847.426.035.293.551.245.843.928.918.752.768.696.279.344.088.055.617.515.694.349.945.406.677.825.140.814.900.616.105.920.256.438.504.578.013.326.493.565.836.047.242.407.382.442.812.245.131.517.757.519.164.899.226.365.743.722.432.277.368.075.027.627.883.045.206.501.792.761.700.945.699.168.497.257.879.683.851.737.049.996.900.961.120.515.655.050.115.561.271.491.492.515.342.105.748.966.629.547.032.786.321.505.730.828.430.221.664.970.324.396.138.635.251.626.409.516.168.005.427.623.435.996.308.921.691.446.181.187.406.395.310.665.404.885.739.434.832.877.428.167.407.495.370.993.511.868.756.359.970.390.117.021.823.616.749.458.620.969.857.006.263.612.082.706.715.408.157.066.575.137.281.027.022.310.927.564.910.276.759.160.520.878.304.632.411.049.364.568.754.920.967.322.982.459.184.763.427.383.790.272.448.438.018.526.977.764.941.072.715.611.580.434.690.827.459.339.991.961.414.242.741.410.599.117.426.060.556.483.763.756.314.527.611.362.658.628.383.368.621.157.993.638.020.878.537.675.545.336.789.915.694.234.433.955.666.315.070.087.213.535.470.255.670.312.004.130.725.495.834.508.357.439.653.828.936.077.080.978.550.578.912.967.907.352.780.054.935.621.561.090.795.845.172.954.115.972.927.479.877.527.738.560.008.204.118.558.930.004.777.748.727.761.853.813.510.493.840.581.861.598.652.211.605.960.308.356.405.941.821.189.714.037.868.726.219.481.498.727.603.653.616.298.856.174.822.413.033.485.438.785.324.024.751.419.417.183.012.281.078.209.729.303.537.372.804.574.372.095.228.703.622.776.363.945.290.869.806.258.422.355.148.507.571.039.619.387.449.629.866.808.188.769.662.815.778.153.079.393.179.093.143.648.340.761.738.581.819.563.002.994.422.790.754.955.061.288.818.308.430.079.648.693.232.179.158.765.918.035.565.216.157.115.402.992.120.276.155.607.873.107.937.477.466.841.528.362.987.708.699.450.152.031.231.862.594.203.085.693.838.944.657.061.346.236.704.234.026.821.102.958.954.951.197.087.076.546.186.622.796.294.536.451.620.756.509.351.018.906.023.773.821.539.532.776.208.676.978.589.731.966.330.308.893.304.665.169.436.185.078.350.641.568.336.944.530.051.437.491.311.298.834.367.265.238.595.404.904.273.455.928.723.949.525.227.184.617.404.367.854.754.610.474.377.019.768.025.576.605.881.038.077.270.707.717.942.221.977.090.385.438.585.844.095.492.116.099.852.538.903.974.655.703.943.973.086.090.930.596.963.360.767.529.964.938.414.598.185.705.963.754.561.497.355.827.813.623.833.288.906.309.004.288.017.321.424.808.663.962.671.333.528.009.232.758.350.873.059.614.118.723.781.422.101.460.198.615.747.386.855.096.896.089.189.180.441.339.558.524.822.867.541.113.212.638.793.675.567.650.340.362.970.031.930.023.397.828.465.318.547.238.244.232.028.015.189.689.660.418.822.976.000.815.437.610.652.254.270.163.595.650.875.433.851.147.123.214.227.266.605.403.581.781.469.090.806.576.468.950.587.661.997.186.505.665.475.715.792.897 |
| 14 | 4933 | 1.189.731.495.357.231.765.085.759.326.628.007.130.763.444.687.096.510.237.472.674.821.233.261.358.180.483.686.904.488.595.472.612.039.915.115.437.484.839.309.258.897.667.381.308.687.426.274.524.698.341.565.006.080.871.634.366.004.897.522.143.251.619.531.446.845.952.345.709.482.135.847.036.647.464.830.984.784.714.280.967.845.614.138.476.044.338.404.886.122.905.286.855.313.236.158.695.999.885.790.106.357.018.120.815.363.320.780.964.323.712.757.164.290.613.406.875.202.417.365.323.950.267.880.089.067.517.372.270.610.835.647.545.755.780.793.431.622.213.451.903.817.859.630.690.311.343.850.657.539.360.649.645.193.283.178.291.767.658.965.405.285.113.556.134.369.793.281.725.888.015.908.414.675.289.832.538.063.419.234.888.599.898.980.623.114.025.121.674.472.051.872.439.321.323.198.402.942.705.341.366.951.274.739.014.593.816.898.288.994.445.173.400.364.617.928.377.138.074.411.345.791.848.573.595.077.170.437.644.191.743.889.644.885.377.684.738.322.240.608.239.079.061.399.475.675.334.739.784.016.491.742.621.485.229.014.847.672.335.977.897.158.397.334.226.349.734.811.441.653.077.758.250.988.926.030.894.789.604.676.153.104.257.260.141.806.823.027.588.003.441.951.455.327.701.598.071.281.589.597.169.413.965.608.439.504.983.171.255.062.282.026.626.200.048.042.149.808.200.002.060.993.433.681.237.623.857.880.627.479.727.072.877.482.838.438.705.048.034.164.633.337.013.385.405.998.040.701.908.662.387.301.605.018.188.262.573.723.766.279.240.798.931.717.708.807.901.740.265.407.930.976.419.648.877.869.604.017.517.691.938.687.988.088.008.944.251.258.826.969.688.364.194.133.945.780.157.844.364.946.052.713.655.454.906.327.187.428.531.895.100.278.695.119.323.496.808.703.630.436.193.927.592.692.344.820.812.834.297.364.478.686.862.064.169.042.458.555.136.532.055.050.508.189.891.866.846.863.799.917.647.547.291.371.573.500.701.015.197.559.097.453.040.033.031.520.683.518.216.494.195.636.696.077.748.110.598.284.901.343.611.469.214.274.121.810.495.077.979.275.556.645.164.983.850.062.051.066.517.084.647.369.464.036.640.569.339.464.837.172.183.352.956.873.912.042.640.003.611.618.789.278.195.710.052.094.562.761.306.703.551.840.330.110.645.101.995.435.167.626.688.669.627.763.820.604.342.480.357.906.415.354.212.732.946.756.073.006.907.088.870.496.125.050.068.156.659.252.761.297.664.065.498.347.492.661.798.824.062.312.210.409.274.584.565.587.264.846.417.650.160.123.175.874.034.726.261.957.289.081.466.197.651.553.830.744.424.709.698.634.753.627.770.356.227.126.145.052.549.125.229.448.040.149.114.795.681.359.875.968.512.808.575.244.271.871.455.454.084.894.986.155.020.794.806.980.939.215.658.055.319.165.641.681.105.966.454.159.951.476.908.583.129.721.503.298.816.585.142.073.061.480.888.021.769.818.338.417.129.396.878.371.459.575.846.052.583.142.928.447.249.703.698.548.125.295.775.920.936.450.022.651.427.249.949.580.708.203.966.082.847.550.921.891.152.133.321.048.011.973.883.636.577.825.533.325.988.852.156.325.439.335.021.315.312.134.081.390.451.021.255.363.707.903.495.916.963.125.924.201.167.877.190.108.935.255.914.539.488.216.897.117.943.269.373.608.639.074.472.792.751.116.715.127.106.396.425.081.353.553.137.213.552.890.539.802.602.978.645.319.795.100.976.432.939.091.924.660.228.878.912.900.654.210.118.287.298.298.707.382.159.717.184.569.540.515.403.029.173.307.292.454.391.789.568.674.219.640.761.451.173.600.617.752.186.991.913.366.837.033.887.201.582.071.625.868.247.133.104.513.315.097.274.713.442.728.340.606.642.890.406.496.636.104.443.217.752.811.227.470.029.162.858.093.727.701.049.646.499.540.220.983.981.932.786.613.204.254.226.464.243.689.610.107.429.923.197.638.681.545.837.561.773.535.568.984.536.053.627.234.424.277.105.760.924.864.023.781.629.665.526.314.910.906.960.488.073.475.217.005.121.136.311.870.439.925.762.508.666.032.566.213.750.416.695.719.919.674.223.210.606.724.721.373.471.234.021.613.540.712.188.239.909.701.971.943.944.347.480.314.217.903.886.317.767.779.921.539.892.177.334.344.368.907.550.318.800.833.546.852.344.370.327.089.284.147.501.640.589.448.482.001.254.237.386.680.074.457.341.910.933.774.891.959.681.016.516.069.106.149.905.572.425.810.895.586.938.833.067.490.204.900.368.624.166.301.968.553.005.687.040.285.095.450.484.840.073.528.643.826.570.403.767.157.286.512.380.255.109.954.518.857.013.476.588.189.300.004.138.849.715.883.139.866.071.547.574.816.476.727.635.116.435.462.804.401.112.711.392.529.180.570.794.193.422.686.818.353.212.799.068.972.247.697.191.474.268.157.912.195.973.794.192.807.298.886.952.361.100.880.264.258.801.320.928.040.011.928.153.970.801.130.741.339.550.003.299.015.924.978.259.936.974.358.726.286.143.980.520.112.454.369.271.114.083.747.919.007.803.406.596.321.353.417.004.068.869.443.405.472.140.675.963.640.997.405.009.225.803.505.672.726.465.095.506.267.339.268.892.424.364.561.897.661.906.898.424.186.770.491.035.344.080.399.248.327.097.911.712.881.140.170.384.182.058.601.614.758.284.200.750.183.500.329.358.499.691.864.066.590.539.660.709.069.537.381.601.887.679.046.657.759.654.588.001.937.117.771.344.698.326.428.792.622.894.338.016.112.445.533.539.447.087.462.049.763.409.147.542.099.248.815.521.395.929.388.007.711.172.017.894.897.793.706.604.273.480.985.161.028.815.458.787.911.160.979.113.422.433.557.549.170.905.442.026.397.275.695.283.207.305.331.845.419.990.749.347.810.524.006.194.197.200.591.652.147.867.193.696.254.337.864.981.603.833.146.354.201.700.628.817.947.177.518.115.217.674.352.016.511.172.347.727.727.075.220.056.177.748.218.928.597.158.346.744.541.337.107.358.427.757.919.660.562.583.883.823.262.178.961.691.787.226.118.865.632.764.934.288.772.405.859.754.877.759.869.235.530.653.929.937.901.193.611.669.007.472.354.746.360.764.601.872.442.031.379.944.139.824.366.828.698.790.212.922.996.174.192.728.625.891.720.057.612.509.349.100.482.545.964.152.046.477.925.114.446.500.732.164.109.099.345.259.799.455.690.095.576.788.686.397.487.061.948.854.749.024.863.607.921.857.834.205.793.797.188.834.779.656.273.479.112.388.585.706.424.836.379.072.355.410.286.787.018.527.401.653.934.219.888.361.061.949.671.961.055.068.686.961.468.019.035.629.749.424.086.587.195.041.004.404.915.266.476.272.761.070.511.568.387.063.401.264.136.517.237.211.409.916.458.796.347.624.949.215.904.533.937.210.937.520.465.798.300.175.408.017.538.862.312.719.042.361.037.129.338.896.586.028.150.046.596.078.872.444.365.564.480.545.689.033.575.955.702.988.396.719.744.528.212.984.142.578.483.954.005.084.264.327.730.840.985.420.021.409.069.485.412.320.805.268.520.094.146.798.876.110.414.583.170.390.473.982.488.899.228.091.818.213.934.288.295.679.717.369.943.152.460.447.027.290.669.964.066.817 |
Wegen
hat die Fermatzahl
doppelt so viele oder um eine weniger als doppelt so viele Stellen wie ihre
Vorgängerin
.
Fermatsche Primzahlen
Die Idee hinter Fermatschen Primzahlen ist der Satz, dass
nur für
mit
prim sein kann:
Beweis durch Widerspruch: Man führt die Annahme, dass das zu Beweisende falsch sei, zu einem Widerspruch.
- Annahme:
ist prim und die Hochzahl
hat einen ungeraden Teiler
.
- Dann gilt
- mit einer ganzen Zahl
. Nach Annahme ist
ungerade, also ist diese Summe bekanntlich durch die Summe
der beiden Basen teilbar:
- Weil die Zahl
prim ist, muss ihr Teiler
gleich 1 oder gleich
sein. Aber in Widerspruch dazu ist
(wegen
) größer als 1 und (wegen
) kleiner als
. Die Annahme, dass
prim ist und
einen ungeraden Teiler
hat, muss daher fallengelassen werden:
kann nur prim sein, wenn
eine Zweierpotenz
mit
ist, was zu zeigen war.
Die Umkehrung dieses Satzes, dass also jede Fermat-Zahl
prim sei, ist falsch.
bis
sind sogar die einzigen bisher bekannten Fermatschen Primzahlen:
Schon Fermat zeigte, dass diese ersten fünf Fermat-Zahlen Primzahlen sind, und vermutete 1640, dass dies auf alle Fermat-Zahlen zutreffe. Diese Vermutung wurde aber schon 1732 von Leonhard Euler einfach widerlegt, indem er mit 641 einen echten Teiler von F5 = 4.294.967.297 fand.
Man vermutet inzwischen, dass außer den ersten fünf keine weiteren Fermatschen Primzahlen existieren. Diese Vermutung beruht auf statistischen Abschätzungen: Der Primzahlsatz besagt, dass die Anzahl der Primzahlen, die nicht größer als x sind, näherungsweise gleich x / ln x ist. Die Primzahldichte oder Wahrscheinlichkeit dafür, dass Fn als ungerade Zahl eine Primzahl ist, beträgt daher näherungsweise 2 / ln Fn ≈ 3/2n. Die Wahrscheinlichkeit, dass die Fermatzahl Fn oder eine der folgenden Fermatzahlen eine Primzahl ist, ergibt sich durch Summation der geometrische Reihe ungefähr zu 6/2n.
Für verbliebene weder teilweise noch vollständig faktorisierte Fermat-Zahlen ist diese Wahrscheinlichkeit mit etwa 6 · 10−10 mittlerweile aber sehr klein geworden.
Faktorisierungsergebnisse von Fermat-Zahlen
Die Zahlen F0 bis F4 sind, wie schon Fermat erkannt hat, Primzahlen:
| n | Fermat-Primzahl Fn |
|---|---|
| 0 | 3 |
| 1 | 5 |
| 2 | 17 |
| 3 | 257 |
| 4 | 65537 |
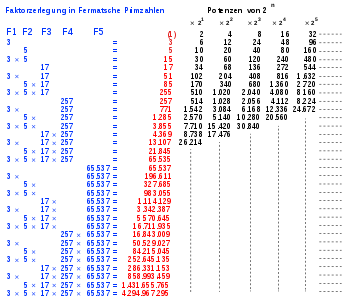
Die Zahlen F5 bis F11 sind entgegen der Vermutung Fermats zusammengesetzt. Sie sind bereits vollständig faktorisiert:
| n | Entdecker der Faktoren | Primfaktorenzerlegung von Fn |
|---|---|---|
| 5 | Leonhard Euler (1732) | 4.294.967.297 (10 Stellen) = 641 (3 Stellen) × 6.700.417 (7 Stellen) |
| 6 | Clausen (1855), Landry & Le Lasseur (1880) |
18.446.744.073.709.551.617 (20 Stellen) = 274.177 (6 Stellen) × 67.280.421.310.721 (14 Stellen) |
| 7 | Morrison & Brillhart (1970) | 340.282.366.920.938.463.463.374.607.431.768.211.457 (39 Stellen) = 59.649.589.127.497.217 (17 Stellen) × 5.704.689.200.685.129.054.721 (22 Stellen) |
| 8 | Brent & Pollard (1980) | 115.792.089.237.316.195.423.570.985.008.687.907.853.269.984.665.640.564.039.457.584.007.913.129.639.937 (78 Stellen) = 1.238.926.361.552.897 (16 Stellen) × 93.461.639.715.357.977.769.163.558.199.606.896.584.051.237.541.638.188.580.280.321 (62 Stellen) |
| 9 | Western (1903), Lenstra & Manasse (1990) |
13.407.807.929.942.597.099.574.024.998.205.846.127.479.365.820.592.393.377.723.561.443.721.764.030.073.546.976.801.874.298.166.903.427.690.031. 858.186.486.050.853.753.882.811.946.569.946.433.649.006.084.097 (155 Stellen) = 2.424.833 (7 Stellen) × 7.455.602.825.647.884.208.337.395.736.200.454.918.783.366.342.657 (49 Stellen) × 741.640.062.627.530.801.524.787.141.901.937.474.059.940.781.097.519.023.905.821.316.144.415.759.504.705.008.092.818.711.693.940.737 (99 Stellen) |
| 10 | Selfridge (1953), Brillhart (1962), Brent (1995) |
179.769.313.486.231.590.772.930 … 304.835.356.329.624.224.137.217 (309 Stellen) = 45.592.577 (8 Stellen) × 6.487.031.809 (10 Stellen) × 4.659.775.785.220.018.543.264.560.743.076.778.192.897 (40 Stellen) × 130.439.874.405.488.189.727.484 … 806.217.820.753.127.014.424.577 (252 Stellen) |
| 11 | Cunningham (1899), Brent & Morain (1988) |
32.317.006.071.311.007.300.714.8 … 193.555.853.611.059.596.230.657 (617 Stellen) = 319.489 (6 Stellen) × 974.849 (6 Stellen) × 167.988.556.341.760.475.137 (21 Stellen) × 3.560.841.906.445.833.920.513 (22 Stellen) × 173.462.447.179.147.555.430.258 … 491.382.441.723.306.598.834.177 (564 Stellen) |
Ab F12 ist keine Fermat-Zahl mehr vollständig faktorisiert. Die ersten drei lauten:
| n | Entdecker der Faktoren | Primfaktorenzerlegung von Fn |
|---|---|---|
| 12 | Lucas
& Pervushin
(1877), Western (1903), Hallyburton & Brillhart (1974), Baillie (1986), Vang, Zimmermann & Kruppa (2010) |
1.044.388.881.413.152.506.691.752.710.716 … 340.403.154.190.337 (1234 Stellen)
= 114.689 (6 Stellen)
× 26.017.793 (8 Stellen)
× 63.766.529 (8 Stellen)
× 190.274.191.361 (12 Stellen)
× 1.256.132.134.125.569 (16 Stellen) |
| 13 | Hallyburton
& Brillhart
(1974), Crandall (1991), Brent (1995) |
1.090.748.135.619.415.929.462.984.244.733 … 665.475.715.792.897 (2467 Stellen)
= 2.710.954.639.361 (13 Stellen)
× 2.663.848.877.152.141.313 (19 Stellen) |
| 14 | Rajala & Woltman (2010) | 1.189.731.495.357.231.765.085.759.326.628 … 290.669.964.066.817 (4933 Stellen)
= 116.928.085.873.074.369.829.035.993.834.596.371.340.386.703.423.373.313 (54 Stellen) × zusammengesetzte Zahl (4880 Stellen) |
Von F12 bis F32 und von einigen größeren Fermat-Zahlen ist bekannt, dass sie zusammengesetzt sind – hauptsächlich, weil ein oder mehrere Faktoren gefunden wurden. Von zwei Fermat-Zahlen (F20 und F24) kennt man zwar keinen Faktor, hat aber auf andere Art gezeigt, dass sie zusammengesetzt sind.
Für F14 wurde am 3. Februar 2010 ein Faktor veröffentlicht, für F22 am 25. März 2010.
Die kleinste Fermat-Zahl, von der bislang nicht bekannt ist, ob sie prim oder zusammengesetzt ist, ist F33. Diese Zahl hat 2.585.827.973 Stellen.
F18.233.954 ist die größte Fermat-Zahl, von der ein Faktor bekannt ist, nämlich die Primzahl 7 · 218.233.956 + 1. Dieser Faktor wurde am 5. Oktober 2020 von Ryan Propper mit Computer-Programmen von Geoffrey Reynolds, Jean Penné und Jim Fougeron entdeckt und hat 5.488.969 Stellen. Die Fermat-Zahl F18.233.954 selbst hat allerdings mehr als 105.488.966 Stellen.
Es gibt keine sinnvolle Methode, sich die Menge an Papier, die man benötigt sie aufzuschreiben – oder gar die Zahl selber – vorzustellen: Selbst mit den hypothetisch kleinsten Teilchen aufgeschrieben, ist das Universum spätestens mit F615 vollgeschrieben und für jeden weiteren Schritt bis F18233954 würde sich der Platz zum Aufschreiben jeweils verdoppeln. Nur hat man mit F615 ja quasi damit noch nicht mal richtig angefangen! Ein wissenschaftlicher Taschenrechner würde eine etwa 27 Kilometer lange Zeile oder alternativ eine 27 Meter mal 10 Meter große Tafel allein für das Anschreiben der Anzahl der Stellen, also von 105488966, als Dezimalzahl benötigen.
Insgesamt weiß man von 311 Fermat-Zahlen, dass sie zusammengesetzt sind. 355 Primfaktoren sind bisher bekannt (Stand: 1. Januar 2021).
Der folgenden Tabelle kann man entnehmen, in welchem Intervall wie viele zusammengesetzte Fermat-Zahlen bekannt sind (Stand: 1. Januar 2021):
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Die kleinsten 25 Fermat-Primfaktoren sind die folgenden:
- 3, 5, 17, 257, 641, 65537, 114689, 274177, 319489, 974849, 2424833,
6700417, 13631489, 26017793, 45592577, 63766529, 167772161, 825753601,
1214251009, 6487031809, 70525124609, 190274191361, 646730219521,
2710954639361, 2748779069441, … (Folge
 A023394 in OEIS)
A023394 in OEIS)
Um von einer Fermat-Zahl nachzuweisen, dass sie zusammengesetzt ist, benutzt man in der Regel den Pépin-Test und den Suyama-Test, die beide besonders auf diese Zahlen zugeschnitten und sehr schnell sind.
Die folgenden 16 Primfaktoren von Fermat-Zahlen wurden vor 1950 entdeckt.
| Jahr | Entdecker | Fermat- Zahl |
Dezimal- stellen von Fn |
Faktor | Dezimal- stellen dieses Faktors |
Faktor ausgeschrieben |
|---|---|---|---|---|---|---|
| 1732 | Leonhard Euler | F5 (a) | 10 | 5 · 27 + 1 | 3 | 641 |
| 1732 | Leonhard Euler | F5 (a) | 10 | 52347 · 27 + 1 | 7 | 6.700.417 |
| 1855 | Thomas Clausen | F6 (a) | 20 | 1071 · 28 + 1 | 6 | 274.177 |
| 1855 | Thomas Clausen | F6 (a) | 20 | 262814145745 · 28 + 1 | 14 | 67.280.421.310.721 |
| 1877 | Ivan M. Pervushin | F12 | 1.234 | 7 · 214 + 1 | 6 | 114.689 |
| 1878 | Ivan M. Pervushin | F23 | 2.525.223 | 5 · 225 + 1 | 9 | 167.772.161 |
| 1886 | Paul Peter Heinrich Seelhoff | F36 | 20.686.623.784 | 5 · 239 + 1 | 13 | 2.748.779.069.441 |
| 1899 | Allan Joseph Champneys Cunningham | F11 | 617 | 39 · 213 + 1 | 6 | 319.489 |
| 1899 | Allan Joseph Champneys Cunningham | F11 | 617 | 119 · 213 + 1 | 6 | 974.849 |
| 1903 | Alfred Edward Western | F9 | 155 | 37 · 216 + 1 | 7 | 2.424.833 |
| 1903 | Alfred Edward Western | F12 | 1.234 | 397 · 216 + 1 | 8 | 26.017.793 |
| 1903 | Alfred Edward Western | F12 | 1.234 | 973 · 216 + 1 | 8 | 63.766.529 |
| 1903 | Alfred Edward Western | F18 | 78.914 | 13 · 220 + 1 | 8 | 13.631.489 |
| 1903 | James Cullen | F38 | 82.746.495.136 | 3 · 241 + 1 | 13 | 6.597.069.766.657 |
| 1906 | James Caddall Morehead | F73 | 2.843.147.923.723.958.896.933 | 5 · 275 + 1 | 24 | 188.894.659.314.785.808.547.841 |
| 1925 | Maurice Borissowitsch Kraitchik | F15 | 9.865 | 579 · 221 + 1 | 10 | 1.214.251.009 |
Seit 1950 wurden alle weiteren Faktoren durch Einsatz von Computern gefunden.
|
|
|
|
|
|
|
Es wurden somit bisher 339 Primfaktoren von Fermat-Zahlen mit Computern gefunden (Stand: 1. Januar 2021).
Eigenschaften
- Beispiele:
- Der Teiler 641 von F5: 641 = 5 · 27 + 1 = 5 · 128 + 1
- Der Teiler 6700417 von F5: 6700417 = 52347 · 27 + 1 = 52347 · 128 + 1
- Fermat-Zahlen lassen sich auf folgende Arten rekursiv berechnen:
-
für
für
für
für
Zwei der vier Beweise funktionieren mittels vollständiger
Induktion. Man zeigt, dass die Behauptungen für den Anfang gelten
(Induktionsanfang), nimmt an, dass die Behauptung für
gilt (Induktionsvoraussetzung) und beweist, dass die Behauptung dadurch auch für
gelten muss (Induktionsschluss).
Beweis der ersten Behauptung:
für
- Der Beweis funktioniert direkt.
, was zu zeigen war.
Beweis der zweiten Behauptung:
für
- Der Beweis funktioniert mittels vollständiger Induktion.
- Induktionsanfang:
- Induktionsvoraussetzung:
bzw. umgeformt
- Induktionsschluss: zu zeigen:
- Was zu zeigen war.
Beweis der dritten Behauptung:
für
- Der Beweis funktioniert direkt.
- Was zu zeigen war.
Beweis der vierten Behauptung:
für
- Der Beweis funktioniert mittels vollständiger Induktion.
- Induktionsanfang:
- Induktionsvoraussetzung:
- Induktionsschluss: zu zeigen:
- Was zu zeigen war.
- Es gelten folgende Darstellungen
von
:
-
- Jede Fermat-Zahl
mit
ist von der Form
, wobei
positiv ganzzahlig ist. (mit anderen Worten:
)
- Jede Fermat-Zahl
mit
ist von der Form
, wobei
positiv ganzzahlig ist. (mit anderen Worten:
)
- Jede Fermat-Zahl
mit
ist von der Form
, wobei
positiv ganzzahlig ist. (mit anderen Worten:
)
- Jede Fermat-Zahl
mit
ist von der Form
, wobei
positiv ganzzahlig ist. (mit anderen Worten:
)
- Anders formuliert: Mit Ausnahme von
und
endet jede Fermat-Zahl im Dezimalsystem mit der Ziffer 7. Die letzten beiden Ziffern sind 17, 37, 57 oder 97.
- Jede Fermat-Zahl
Beweis der ersten Behauptung:
-
- Der Beweis funktioniert direkt. Man startet mit einer bekannten richtigen Aussage und beweist das Gewünschte.
- Eine weiter oben angegebene Eigenschaft besagt, dass
gilt für
. Somit gilt aber, weil
ist:
.
- Der Ausdruck
ist als Produkt von ungeraden Fermat-Zahlen selber ungerade. Addiert man 1 dazu, erhält man eine gerade Zahl. Also ist
ein Produkt aus 3 und einer geraden Zahl und somit durch 6 teilbar. Es gibt also ein
mit
. Daher ist
von der Form
, was zu zeigen war.
Beweis der zweiten Behauptung:
, was zu zeigen war.
Beweis der dritten Behauptung:
-
- Der dritte Beweis funktioniert mit vollständiger Induktion:
- Induktionsanfang:
- Induktionsvoraussetzung:
- Induktionsschluss: zu zeigen:
für ein
- Was zu zeigen war.
Beweis der vierten Behauptung:
-
- Der vierte Beweis funktioniert direkt:
- Weiter oben wurde gezeigt, dass
für
gilt. Daraus kann man folgern, dass
für
gilt. Im Speziellen gilt also für
(also für
) die Kongruenz
und somit entweder
oder
. Weil aber Fermat-Zahlen immer ungerade sind, kann nur die Kongruenz
zutreffen, was zu zeigen war.
- Die Aussage, dass die letzten beiden Ziffern 17, 37, 57 oder 97 sind,
kann man der Literatur
entnehmen.
- Sei
die
-te Fermat-Zahl. Dann gilt:
-
hat unendlich viele Darstellungen der Form
mit
positiv ganzzahlig, für alle
hat mindestens eine Darstellung der Form
mit
positiv ganzzahlig. Ist
zusammengesetzt, gibt es mehrere Möglichkeiten dieser Darstellung.
kann niemals als Summe von zwei Primzahlen dargestellt werden, für alle
-
für alle
kann niemals als Differenz von zwei p-ten Potenzen geschrieben werden, wenn
und p ungerade Primzahlen sind:
-
für alle
Beweis der ersten Behauptung:
- Der Beweis funktioniert direkt.
- Die Existenz einer solchen Darstellung konnte schon weiter oben mit
und
gezeigt werden:
- Um unendlich viele solche Darstellungen zu erhalten, betrachte man
folgende Identität:
- Weil
ist, gilt
und
. Somit kann man aus dem Darstellungspaar
für
ein (größeres) Darstellungspaar
für
konstruieren. Aus diesem kann man mit obiger Identität das nächste (größere) Darstellungspaar für
konstruieren und so fort. Man erhält also unendlich viele Darstellungspaare für
und somit auch unendlich viele Darstellungen von
der Form
, was zu zeigen war.
Beweis der zweiten Behauptung:
- Der Beweis funktioniert direkt.
- Es gilt:
- Somit hat man zwei Zahlen
und
gefunden, sodass
, also die Differenz von zwei Quadratzahlen, ist, was zu zeigen war.
- Die Aussage, dass es mehrere solche Darstellungsmöglichkeiten als
Differenz von zwei Quadratzahlen gibt, wenn
zusammengesetzt ist, kann man der Literatur entnehmen.
Beweis der dritten Behauptung:
- Der Beweis funktioniert indirekt. Man startet mit einer Behauptung und zeigt, dass sie falsch ist, womit die Behauptung fallengelassen werden muss und das Gegenteil gilt.
- Alle Fermat-Zahlen
sind als Summe einer geraden und einer ungeraden Zahl 1 immer ungerade Zahlen. Primzahlen sind, bis auf die erste Primzahl
, immer ungerade. Wenn also die ungerade Zahl
Summe von zwei Primzahlen sein soll, so dürfen nicht beide Primzahlen ungerade sein, weil die Summe zweier ungerader Zahlen eine gerade Zahl ergibt. Eine davon muss gerade sein. Weil es nur eine gerade Primzahl gibt, muss also 2 eine der beiden Summanden sein. Der andere prime Summand ist somit
und es gilt trivialerweise
. Es gilt aber:
- Somit ist aber
für
zusammengesetzt und keine Primzahl, weil sogar der kleinere der beiden Faktoren
ist und somit eine nichttriviale Faktorisierung von
existiert. Wir erhalten einen Widerspruch. Die Annahme, dass man eine Fermat-Zahl als Summe zweier Primzahlen darstellen kann, muss fallengelassen werden, was zu zeigen war.
Beweis der vierten Behauptung:
- Der Beweis funktioniert indirekt. Man startet mit einer Behauptung und zeigt, dass sie falsch ist, womit die Behauptung fallengelassen werden muss und das Gegenteil gilt.
- Angenommen,
ist eine ungerade Primzahl und
kann dargestellt werden als Differenz von zwei p-ten Potenzen. Es sei also
. Dann gilt:
mit
- Weil
prim ist und somit nicht zwei Teiler haben darf, muss
sein. Wegen des kleinen fermatschen Satzes ist
und
und somit gilt:
- Somit muss
ein Teiler von
sein, was aber nicht sein kann, weil
nur Zweierpotenzen als Teiler hat.
- Die Annahme muss also fallengelassen werden,
kann daher nicht dargestellt werden als Differenz von zwei p-ten Potenzen.
- Was zu zeigen war.
- Sei
die
-te Fermat-Zahl und sei
die Anzahl der Stellen von
. Dann gilt:
-
- wobei mit
die Floor-Funktion gemeint ist (also die größte ganze Zahl, die kleiner oder gleich
ist)
- Sei
die
-te Fermat-Zahl mit
. Dann gilt:
-
ist eine Primzahl genau dann, wenn gilt:
- Mit anderen Worten: Für
gilt:
- Dieser Satz nennt sich Pépin-Test.
Der Beweis funktioniert direkt. Man startet mit dem linken Teil der Aussage und zeigt, dass daraus die rechte folgert. Danach startet man mit dem rechten Teil der Aussage und zeigt, dass daraus die linke Seite folgert.
Beweis:
- „
“: Sei
eine Primzahl mit
. Man muss zeigen, dass
ist.
- Es gilt nach dem Eulerschein Kriterium für das Legendre-Symbol
die folgende Kongruenz:
- Weil
und
gilt (wurde weiter oben bewiesen), erhält man wegen des Quadratischen Reziprozitätsgesetzes für das Legendre-Symbol:
- Somit erhält man:
- Damit ist eine Richtung des obigen Satzes gezeigt worden.
- Es gilt nach dem Eulerschein Kriterium für das Legendre-Symbol
die folgende Kongruenz:
- „
“: Sei nun
. Man muss zeigen, dass
eine Primzahl ist.
- Quadriert man diese Kongruenz, erhält man:
- Nach dem verbesserten
Lucas-Test folgt, dass
prim ist (weil
nur einen einzigen Primteiler, nämlich
hat und für diesen Primfaktor
auch laut Voraussetzung
gilt).
- Quadriert man diese Kongruenz, erhält man:
- Damit sind beide Richtungen obiger Aussage bewiesen, sie hat sich somit
als richtig herausgestellt.
- Für
gilt:
- Sei
,
und
prim. Dann gilt:
Der Beweis funktioniert direkt. Man startet mit einer bekannten richtigen Aussage und beweist mittels Umformungen und Modulo-Rechnungen das Gewünschte.
Beweis der ersten Behauptung:
- Somit gilt:
- Für
erhält man:
- Setzt man nun
in obiges Ergebnis ein, dann erhält man:
- Die Zahl
ist als Potenz von 2 durch jede kleinere Potenz von 2 teilbar, somit für
auch durch
. Es existiert also eine positive ganze Zahl
mit
. Wenn man dies in obiges Ergebnis einsetzt, erhält man:
- Womit die erste Behauptung bewiesen ist.
- Sei
eine Primzahl und
eine ganze Zahl. Dann gilt für jede prime Fermat-Zahl
mit
:
-
teilt
Der Beweis funktioniert direkt. Man startet mit einer bekannten richtigen Aussage und beweist das Gewünschte.
Beweis:
- Sei
eine prime Fermat-Zahl mit
.
- Sei weiters
ein Teiler von
. Dann ist
auch ein Teiler von
und somit auch Teiler der Differenz. Also gilt:
teilt
- Sei nun
kein Teiler von
. Dann gilt wegen des kleinen fermatschen Satzes:
und somit:
teilt
- Weil aber jede kleine Zweierpotenz jede größere Zweierpotenz teilt, gilt auch:
teilt
- Weiters gilt bei mehrfacher Anwendung der dritten binomischen Formel:
teilt
- Obige Ergebnisse zusammengefasst ergibt:
teilt
teilt
teilt
- Sei weiters
- Was zu zeigen war.
- Sei
. Dann gilt:
-
für alle
Der Beweis funktioniert direkt.
Beweis:
- Man betrachte die folgende Identität unter Verwendung der dritten binomischen Formel:
- Wenn man nun
substituiert, sich ins Gedächtnis zurückruft, dass Fermatzahlen die Form
haben und dass laut Definition
ist, erhält man das gewünschte Ergebnis:
- Was zu zeigen war.
- Sei
eine Primzahl. Dann gilt:
-
-
mit einer positiven ganzen Zahl
-
Beweis von Teil 1 durch Widerspruch: Man führt die Annahme, dass das zu Beweisende falsch sei, zu einem Widerspruch (analog zum Beweis weiter oben).
- Annahme:
ist prim und die Hochzahl
hat einen ungeraden Teiler
.
- Dann gilt
- mit einer ganzen Zahl
. Nach Annahme ist
ungerade, also ist diese Summe bekanntlich durch die Summe
der beiden Basen teilbar:
- Weil die Zahl
prim ist, muss ihr Teiler
gleich 1 oder gleich
sein. Aber im Widerspruch dazu ist
(wegen
) größer als 1 und (wegen
) kleiner als
. Die Annahme, dass
prim ist und
einen ungeraden Teiler
hat, muss daher fallengelassen werden:
kann nur prim sein, wenn
eine Zweierpotenz
mit
ist.
- Es ist also
und
ist somit eine Zweierpotenz.
- Es wurde aber weiter
oben gezeigt, dass eine Zahl der Form
nur dann eine Primzahl ist, wenn die Hochzahl (also der Exponent) selbst eine Zweierpotenz ist. Es gibt also ein
, sodass
ist. Somit muss
selbst eine Zweierpotenz (also ohne ungerade Teiler) sein, daher gibt es ein
, sodass
ist. Es ist also
, was als Erstes zu zeigen war.
- Weiters gilt also
, was zu zeigen war.
-
- Beispiele:
- Für
erhält man
- Für
erhält man
- Für
erhält man
(eine 20-stellige Zahl)
- Für
erhält man
(eine 617-stellige Zahl)
- Für
erhält man
(eine 315653-stellige Zahl)
- Auch für
(eine 41373247568-stellige Zahl) und
(die Anzahl der Stellen dieser Zahl hat 620 Stellen) erhält man keine Primzahlen. Für alle anderen
ist noch nicht bekannt, ob es sich um Primzahlen handelt oder nicht.
- Könnte man zeigen, dass es keine weiteren Primzahlen der Form
gibt, so wäre gleichzeitig auch bewiesen, dass es unendlich viele zusammengesetzte Fermat-Zahlen gibt.
- Für
- Beispiele:
- Sei
eine Primzahl. Dann gilt:
-
-
mit einer positiven ganzen Zahl
-
- Die Menge aller quadratischen Nichtreste einer primen Fermat-Zahl ist gleich der Menge aller ihrer Primitivwurzeln.
- Zwei Fermat-Zahlen sind gleich oder teilerfremd, wie aus der letzten Aussage folgt (Goldbachs Theorem, nach Christian Goldbach, 1730). Daraus lässt sich folgern, dass es unendlich viele Primzahlen gibt.
- Die Summe der Kehrwerte aller Fermat-Zahlen ist eine irrationale Zahl (bewiesen von Solomon W. Golomb im Jahr 1963). Es gilt:
- Keine Fermat-Zahl ist eine perfekte Zahl. Keine Fermat-Zahl ist Teil eines Paares befreundeter Zahlen (bewiesen von Florian Luca im Jahr 2000).
- Die Summe der Kehrwerte aller Primteiler von Fermat-Zahlen ist konvergent (bewiesen von Michal Křížek, Florian Luca und Lawrence Somer im Jahr 2002). Mit anderen Worten:
- Sei
die Menge aller Primzahlen, die irgendeine Fermat-Zahl
teilen. Dann gilt:
ist konvergent.
- Sei
der größte Primteiler der Fermat-Zahl
. Dann gilt:
-
- für alle
(bewiesen von Aleksander Grytczuk, Florian Luca und Marek Wójtowicz im Jahr 2001).
- Jede zusammengesetzte Fermat-Zahl ist eine starke Pseudoprimzahl zur Basis 2, weil für alle Fermat-Zahlen gilt:
-
- für mindestens ein
(im Speziellen für
).
- Jede zusammengesetzte Fermat-Zahl ist eine eulersche Pseudoprimzahl zur Basis 2, weil für alle Fermat-Zahlen gilt:
- Jede zusammengesetzte Fermat-Zahl
ist eine fermatsche Pseudoprimzahl zur Basis 2. Das heißt, für alle Fermat-Zahlen gilt:
- Eine prime Fermat-Zahl
ist niemals eine Wieferich-Primzahl. Das heißt, für alle primen Fermat-Zahlen gilt:
- Ein Produkt
-
- von Fermat-Zahlen mit
ist eine fermatsche Pseudoprimzahl zur Basis 2 genau dann, wenn
(bewiesen von Michele Cipolla im Jahr 1904).
- Jede Fermat-Zahl
hat im Binärsystem die Form
-
- mit
Nullen zwischen den beiden Einsern.
Ungelöste Probleme
- Ist Fn eine zusammengesetzte Zahl für alle n ≥ 5?
- Gibt es unendlich viele zusammengesetzte Fermatsche Zahlen? (Diese Behauptung ist etwas schwächer als die vorherige.)
- Gibt es unendlich viele Fermatsche Primzahlen? (Diese Behauptung steht nicht im Widerspruch zur vorherigen; es könnten beide Behauptungen gelten.)
- Gibt es Fermatsche Zahlen, die nicht quadratfrei sind?
Geometrische Anwendung der Fermatschen Primzahlen
Rot: Seitenzahlen der 31 bekannten regulären Polygone mit ungerader Seitenzahl (Lesart von oben nach unten: Gleichseitiges Dreieck – regelmäßiges Fünfeck – regelmäßiges Fünfzehneck - … – 4294967295-Eck)
Schwarz: Seitenzahlen der (unendlich vielen) bekannten Polygone mit gerader Seitenzahl
Carl Friedrich Gauß zeigte (in seinem Lehrbuch Disquisitiones Arithmeticae), dass es einen Zusammenhang zwischen der Konstruktion von regelmäßigen Polygonen und den Fermatschen Primzahlen gibt:
- Ein regelmäßiges Polygon mit n Seiten kann dann und nur dann mit Zirkel und Lineal konstruiert werden, wenn n eine Potenz von 2 oder das Produkt einer Potenz von 2 mit paarweise verschiedenen Fermatschen Primzahlen ist.
Mit anderen Worten:
- Das
-seitige regelmäßige Polygon kann mit Zirkel und Lineal konstruiert werden
mit
und paarweise verschiedenen Fermatschen Primzahlen
Konkret zeigte Gauß die Konstruierbarkeit des regelmäßigen Siebzehnecks.
Die nach der obigen Formel konstruierbaren regelmäßigen Polygone lassen sich
in zwei Gruppen unterteilen: solche mit ungerader Seitenzahl und solche mit
gerader Seitenzahl. Alle Polygone, in denen
ist, sind offensichtlich solche mit gerader Seitenzahl (durch 2 teilbar). Alle
Polygone mit
sind solche mit ungerader Seitenzahl (ein Produkt von Primzahlen größer als 2
ist immer eine ungerade Zahl). Da nur endlich viele Fermatsche Primzahlen
bekannt sind, ist auch die Anzahl der bekannten, mit Zirkel und Lineal
konstruierbaren, regulären Polygone mit ungerader Seitenzahl begrenzt.
Unter diesen ist das 4294967295-Eck
dasjenige mit der größten Eckenzahl.
Verallgemeinerte Fermatsche Zahlen
Eine Zahl der Form
mit zwei teilerfremden
natürlichen Zahlen a > 0 und b > 0 heißt
verallgemeinerte Fermatsche Zahl. Ist eine solche Zahl prim, dann heißt
sie verallgemeinerte Fermatsche Primzahl.
Insgesamt sind schon über 11719 Faktoren von verallgemeinerten zusammengesetzten Fermat-Zahlen bekannt (Stand: 13. August 2018). Davon wurden alleine über 5100 von Anders Björn und Hans Riesel vor 1998 entdeckt.
Ist a = 1, so werden die so erhaltenen verallgemeinerten Fermatschen Zahlen üblicherweise mit
bezeichnet. Die Zahl b nennt man Basis.
Ist a = 1 und b = 2, so handelt es sich um die schon weiter oben erwähnten Fermat-Zahlen
.
Es folgt eine Auflistung der ersten verallgemeinerten Fermatschen Primzahlen
der Form .
Die beiden Basen
und
müssen, damit
prim sein kann, teilerfremd sein. Außerdem ist es auch notwendig, dass man
durch den größten
gemeinsamen Teiler
dividiert, da die Zahl
bei ungeradem
und
immer eine gerade Zahl wäre und somit niemals eine Primzahl sein könnte. Weiters
kann man ohne
Einschränkung annehmen, dass
sein muss, da man bei
das
bedenkenlos mit
vertauschen kann und somit zum Beispiel
ist. Der Fall
führt niemals zu Primzahlen, da dann
wäre und sicher nicht prim ist (es wären in diesem Fall auch die beiden Basen
und
nicht wie vorausgesetzt teilerfremd).
|
|
|
|
Fast
alle verallgemeinerten Fermatschen Zahlen sind wahrscheinlich
zusammengesetzt. Bewiesen ist diese Aussage aber nicht, denn schon für
und
(das sind die ursprünglichen Fermat-Zahlen) wurde weiter oben im Kapitel Ungelöste
Probleme erwähnt, dass man noch nicht weiß, ob ab
alle weiteren
zusammengesetzt sind oder nicht. Ähnlich verhält es sich mit anderen Basen und
Hochzahlen. Und obwohl schon über 11000 Faktoren von verallgemeinerten
Fermatschen Zahlen bekannt sind (siehe weiter oben), ist es schwierig, solche
Faktoren zu finden, zumal
sehr schnell sehr groß wird. Zum Teil weiß man zwar, dass diese Zahlen
zusammengesetzt sein müssen, aber Primteiler kennt man von den wenigsten.
Bekannt ist, dass solche Primteiler die Form
haben müssen. Es folgt eine Auflistung von Primfaktoren kleinerer
verallgemeinerter Fermatschen Zahlen inklusive zweier etwas höherer
Zahlenbeispiele, anhand derer man erkennen kann, wie schnell die Zahlen sehr
hoch werden.
| verallgemeinerte zusammengesetzte Fermatsche Zahl | Primteiler | |||||||
|---|---|---|---|---|---|---|---|---|
| b | a | n | Dezimalschreibweise | k | m | Primteiler |
Dezimalschreibweise | |
| 2 | 1 | 5 | 4.294.967.297 (= |
5 | 7 | 641 | ||
| 52347 | 7 | 6.700.417 | ||||||
| 2 | 1 | 6 | 18.446.744.073.709.551.617 (= |
1071 | 8 | 274.177 | ||
| 262814145745 | 8 | 67.280.421.310.721 | ||||||
| 3 | 1 | 3 | 3.281 | 1 | 4 | 17 | ||
| 3 | 6 | 193 | ||||||
| 3 | 2 | 3 | 6.817 | 1 | 4 | 17 | ||
| 25 | 4 | 401 | ||||||
| 3 | 2 | 4 | 43.112.257 | 95 | 5 | 3.041 | ||
| 443 | 5 | 14.177 | ||||||
| 3 | 2 | 5 | 1.853.024.483.819.137 | 9 | 7 | 1.153 | ||
| 3138931869 | 9 | 1.607.133.116.929 | ||||||
| 3 | 2 | 6 | 3.433.683.820.310.959.228.731.558.640.897 | 3 | 8 | 769 | ||
| 952341149 | 7 | 121.899.667.073 | ||||||
| 286168266760535 | 7 | 36.629.538.145.348.481 | ||||||
| 4 | 1 | 4 | 4.294.967.297 | 5 | 7 | 641 | ||
| 52347 | 7 | 6.700.417 | ||||||
| 4 | 1 | 5 | 18.446.744.073.709.551.617 | 1071 | 8 | 274.177 | ||
| 262814145745 | 8 | 67.280.421.310.721 | ||||||
| 4 | 1 | 6 | 340.282.366.920.938.463.463.374.607.431.768.211.457 | 116503103764643 | 9 | 59.649.589.127.497.217 | ||
| 11141971095088142685 | 9 | 5.704.689.200.685.129.054.721 | ||||||
| 4 | 3 | 1 | 25 | 1 | 2 | 5 | ||
| 1 | 2 | 5 | ||||||
| 4 | 3 | 3 | 72.097 | 1 | 4 | 17 | ||
| 265 | 4 | 4.241 | ||||||
| 4 | 3 | 5 | 18.448.597.093.898.403.457 | 187 | 6 | 11.969 | ||
| 24083827353343 | 6 | 1.541.364.950.613.953 | ||||||
| 4 | 3 | 6 | 340.282.370.354.622.283.755.887.092.089.617.300.737 | 1317 | 8 | 337.153 | ||
| 492813355211781926870528348211 | 11 | 1.009.281.751.473.729.386.230.842.057.136.129 | ||||||
| 5 | 1 | 3 | 195.313 | 1 | 4 | 17 | ||
| 359 | 5 | 11.489 | ||||||
| 5 | 1 | 4 | 76.293.945.313 | 81 | 5 | 2.593 | ||
| 459735 | 6 | 29.423.041 | ||||||
| 5 | 1 | 5 | 11.641.532.182.693.481.445.313 | 5 | 7 | 641 | ||
| 1172953 | 6 | 75.068.993 | ||||||
| 945042975 | 8 | 241.931.001.601 | ||||||
| 5 | 1 | 6 | 271.050.543.121.376.108.501.863.200.217.485.427.856.445.313 (Zahl hat 45 (also abgerundet etwa |
3 | 8 | 769 | ||
| 28644528117 | 7 | 3.666.499.598.977 | ||||||
| 187759681216101058498487625 | 9 | 96.132.956.782.643.741.951.225.664.001 | ||||||
| … | … | … | … | … | … | … | … | … |
| … | … | … | … | |||||
| 12 | 11 | 37 | Zahl hat 148.321.541.064 (also etwa |
1776222707793 | 38 | 488.244.380.184.543.957.614.593 | ||
| und noch ein Faktor, von dem man nicht weiß, ob er zusammengesetzt ist oder nicht | ||||||||
| … | … | … | … | … | … | … | … | … |
| … | … | … | … | |||||
| 12 | 11 | 7033640 | Zahl hat etwa |
3 | 7033641 | Primteiler hat 2117338 Stellen | ||
| und noch ein Faktor, von dem man nicht weiß, ob er zusammengesetzt ist oder nicht | ||||||||
Verallgemeinerte Fermatsche Zahlen der Form Fn(b)
Ist b eine gerade Zahl, so kann Fn(b) sowohl zusammengesetzt als auch prim sein.
Beispiel 1:
- b = 8, n = 3 ergibt die zusammengesetzte Zahl
.
Beispiel 2:
- b = 6, n = 2 ergibt die Primzahl
.
Beispiel 3:
- b = 30, n = 5 ergibt die 48-stellige Primzahl
- und ist gleichzeitig die kleinste verallgemeinerte Fermatsche Primzahl mit
.
Ist b eine ungerade Zahl, so ist Fn(b) als Summe einer Potenz einer ungeraden Zahl (die selbst wieder ungerade ist) und 1 immer eine gerade Zahl, somit durch 2 teilbar und deshalb für b > 1 keine Primzahl, sondern zusammengesetzt. In diesem Fall wird häufig die Zahl
auf ihre Primalität untersucht. Diese Zahlen werden auch halbe verallgemeinerte Fermatsche Zahlen genannt.
Beispiel 4:
- b = 3, n = 2 ergibt die gerade und somit zusammengesetzte
Zahl
.
- Es ist aber
- eine Primzahl.
Beispiel 5:
- b = 5, n = 3 ergibt die gerade und somit zusammengesetzte
Zahl
- Es ist aber
- eine zusammengesetzte Zahl.
Liste der Primzahlen der Form Fn(b)
Verallgemeinerte Fermatsche Zahlen der Form
(für gerade
)
bzw. der Form
(für ungerade
)
sind in den meisten Fällen zusammengesetzt. Weil diese Zahlen sehr schnell sehr
groß werden, sind nicht besonders viele Primzahlen dieser Art bekannt. Es folgt
eine Auflistung von Primzahlen der Form
mit konstantem
:
|
|
|
|
Die kleinsten
(ab
),
für die
bzw.
erstmals eine Primzahl ergibt, kann man der obigen Tabelle entnehmen, was für
alle
die folgende Liste ergibt (der Wert −1 bedeutet „nicht existent“ bzw. „noch
keine bekannt“):
- 0, 0, 0, 0, 0, 2, −1, 0, 0, 1, 0, 0, 1, 1, 0, 2, 0, 1, 1, 0, 0, 2,
1, 0, 1, −1, 0, 1, 0, −1, −1,
0, 2, 1, 0, 0, −1, 1, 0, 4, 0, 3, 4, 0, 0, 3,
2, 1, −1, 1, 0, 3, 1, −1,
1, 0, 0, 1, 0, … (Folge
 A253242
in OEIS)
A253242
in OEIS)
Mehr Informationen für gerade
bis zur Basis
findet man im Internet.
Nun folgt eine Auflistung von Primzahlen der Form
mit konstantem
:
| n | Fn(b) | b, für die Fn(b) prim ist | OEIS-Folge |
|---|---|---|---|
| 0 | 1, 2, 4, 6, 10, 12, 16, 18, 22, 28, 30, 36,
40, 42, 46, 52, 58, 60, 66, 70, 72, 78, 82, 88, 96, 100, 102, 106, 108,
112, 126, 130, 136, 138, 148, 150, 156, 162, 166, 172, 178, 180, 190, 192,
196, 198, 210, 222, 226, 228, 232, 238, 240, 250, 256, 262, 268,
270, … (alle Primzahlen minus 1) |
(Folge | |
| 1 | 1, 2, 4, 6, 10, 14, 16, 20, 24, 26, 36, 40, 54, 56, 66, 74, 84, 90, 94, 110, 116, 120, 124, 126, 130, 134, 146, 150, 156, 160, 170, 176, 180, 184, 204, 206, 210, 224, 230, 236, 240, 250, 256, 260, 264, 270, 280, 284, 300, 306, 314, 326, 340, 350, 384, 386, 396, … | (Folge | |
| 2 | 1, 2, 4, 6, 16, 20, 24, 28, 34, 46, 48, 54, 56, 74, 80, 82, 88, 90, 106, 118, 132, 140, 142, 154, 160, 164, 174, 180, 194, 198, 204, 210, 220, 228, 238, 242, 248, 254, 266, 272, 276, 278, 288, 296, 312, 320, 328, 334, 340, 352, 364, 374, 414, 430, 436, 442, 466, … | (Folge | |
| 3 | 1, 2, 4, 118, 132, 140, 152, 208, 240, 242, 288, 290, 306, 378, 392, 426, 434, 442, 508, 510, 540, 542, 562, 596, 610, 664, 680, 682, 732, 782, 800, 808, 866, 876, 884, 892, 916, 918, 934, 956, 990, 1022, 1028, 1054, 1106, 1120, 1174, 1224, 1232, 1256, 1284, … | (Folge | |
| 4 | 1, 2, 44, 74, 76, 94, 156, 158, 176, 188, 198, 248, 288, 306, 318, 330, 348, 370, 382, 396, 452, 456, 470, 474, 476, 478, 560, 568, 598, 642, 686, 688, 690, 736, 774, 776, 778, 790, 830, 832, 834, 846, 900, 916, 946, 956, 972, 982, 984, 1018, 1044, 1078, … | (Folge | |
| 5 | 1, 30, 54, 96, 112, 114, 132, 156, 332, 342, 360, 376, 428, 430, 432, 448, 562, 588, 726, 738, 804, 850, 884, 1068, 1142, 1198, 1306, 1540, 1568, 1596, 1678, 1714, 1754, 1812, 1818, 1878, 1906, 1960, 1962, 2046, 2098, 2118, 2142, 2330, 2418, 2434, 2654, 2668, … | (Folge | |
| 6 | 1, 102, 162, 274, 300, 412, 562, 592, 728, 1084, 1094, 1108, 1120, 1200, 1558, 1566, 1630, 1804, 1876, 2094, 2162, 2164, 2238, 2336, 2388, 2420, 2494, 2524, 2614, 2784, 3024, 3104, 3140, 3164, 3254, 3278, 3628, 3694, 3738, 3750, 4000, 4030, 4058, 4166, … | (Folge | |
| 7 | 1, 120, 190, 234, 506, 532, 548, 960, 1738, 1786, 2884, 3000, 3420, 3476, 3658, 4258, 5788, 6080, 6562, 6750, 7692, 8296, 9108, 9356, 9582, 9706, 10238, 10994, 11338, 11432, 11466, 11554, 11778, 12704, 12766, 13082, 13478, 13700, … | (Folge | |
| 8 | 1, 278, 614, 892, 898, 1348, 1494, 1574, 1938, 2116, 2122, 2278, 2762, 3434, 4094, 4204, 4728, 5712, 5744, 6066, 6508, 6930, 7022, 7332, 8524, 8644, 8762, 8808, 9024, 9142, 9412, 10892, 12206, 13220, 13222, 13246, 13370, 13738, 14114, 14930, … | (Folge | |
| 9 | 1, 46, 1036, 1318, 1342, 2472, 2926, 3154, 3878, 4386, 4464, 4474, 4482, 4616, 4688, 5374, 5698, 5716, 5770, 6268, 6386, 6682, 7388, 7992, 8678, 8792, 9448, 9452, 9972, 10086, 10448, 10926, 11468, 12754, 13198, 13776, 14734, 16826, 16914, 18334, … | (Folge | |
| 10 | 1, 824, 1476, 1632, 2462, 2484, 2520, 3064, 3402, 3820, 4026, 6640, 7026, 7158, 9070, 12202, 12548, 12994, 13042, 15358, 17646, 17670, 18336, 19564, 20624, 22500, 24126, 26132, 26188, 26240, 29074, 29658, 30778, 31126, 32244, 33044, 34016, … | (Folge | |
| 11 | 1, 150, 2558, 4650, 4772, 11272, 13236, 15048, 23302, 26946, 29504, 31614, 33308, 35054, 36702, 37062, 39020, 39056, 43738, 44174, 45654, 46502, 47348, 49190, 49204, 49544, 54514, 57210, 59770, 61184, 66894, 68194, 70574, 72446, 82642, … | (Folge | |
| 12 | 1, 1534, 7316, 17582, 18224, 28234, 34954, 41336, 48824, 51558, 51914, 57394, 61686, 62060, 89762, 96632, 98242, 100540, 101578, 109696, 110540, 114690, 125440, 125442, 127596, 138068, 144362, 154908, 157310, 161822, 161900, 166224, … | (Folge | |
| 13 | 1, 30406, 71852, 85654, 111850, 126308, 134492, 144642, 147942, 150152, 165894, 176206, 180924, 201170, 212724, 222764, 225174, 241600, 241860, 248744, 268032, 270674, 302368, 316970, 326260, 347962, 350830, 397468, 410938, 416010, 441238, 443718, 458520, 462678, 463012, 475158, 481750, … | (Folge | |
| 14 | 1, 67234, 101830, 114024, 133858, 162192, 165306, 210714, 216968, 229310, 232798, 422666, 426690, 449732, 462470, 468144, 498904, 506664, 509622, 528614, 572934, 581424, 638980, 641762, 656210, 698480, 704930, 730352, 795810, 840796, 908086, 975248, 976914, 990908, 1007874, 1037748, 1039970, 1067896, 1082054, 1097352, 1102754, 1132526, 1162996, 1171010, 1177808, 1181388, … | (Folge | |
| 15 | 1, 70906, 167176, 204462, 249830, 321164, 330716, 332554, 429370, 499310, 524552, 553602, 743788, 825324, 831648, 855124, 999236, 1041870, 1074542, 1096382, 1113768, 1161054, 1167528, 1169486, 1171824, 1210354, 1217284, 1277444, 1519380, 1755378, 1909372, 1922592, 1986700, 2034902, 2147196, 2167350, …, 3292665455999520712131951642528, … | (Folge | |
| 16 | 1, 48594, 108368, 141146, 189590, 255694, 291726, 292550, 357868, 440846, 544118, 549868, 671600, 843832, 857678, 1024390, 1057476, 1087540, 1266062, 1361846, 1374038, 1478036, 1483076, 1540550, 1828502, 1874512, 1927034, 1966374, 2019300, 2041898, 2056292, 2162068, 2177038, 2187182, 2251082, 2313394, …, 1814570322984178, … | (Folge | |
| 17 | 1, 62722, 130816, 228188, 386892, 572186, 689186, 909548, 1063730, 1176694, 1361244, 1372930, 1560730, 1660830, 1717162, 1722230, 1766192, 1955556, 2194180, 2280466, 2639850, 3450080, 3615210, 3814944, 4085818, 4329134, 4893072, 4974408, 5326454, 5400728, 5471814, 5586416, 5734100, 5877582, 6391936, 6403134, 6705932, 7379442, 7832704, 7858180, 7926326, 8150484, 8704114, 8770526, 9240606, 9419976, 9785844, 9907326, 10037266, 10368632, 10453790, 10765720, 10921162, 10962066, 10994460, 11036888, 11195602, 11267296, 11292782, 11778792, 11876066, 12343130, 12357518, 12512992, 12661786, 12687374, 12851074, 12961862, 12978952, 13083418, 13433028, 13613070, 13800346, 14020004, 14217182, 14613898, 14790404, 15091270, 15147290, 15237960, 15342502, 15567144, 15667716, 15731520, 16329572, 16741226, 16985784, 17025822, 17052490, …, 42654182, 43163894, 43165206, 44049878, 44085096, 44330870, 44438760, 44919410, 45315256, 45570624, 46077492, 46371508, 46385310, 46413358, 46730280, 46736070, 46776558, 47090246, 47179704, 48273828, 48370248, 48643706, 49038514, 49090656, 49225986, 49243622, 49331672, 49397682, 49530004, 49817700, 50055102, 50110436, 50217306, 50495632, 50844724, 50963598, 51269192, 51567684, 51570250, 51580416, 51872628, 51954384, 52043532, 52412612, 52712138, 53078434, 53161266, 53659976, 54032538, 54161106, 54206254, 54212352, 54334044, 54361742, 54548788, 55015050, 55184170, 55268442, 55579418, 55645700, 56307420, 56383242, 56459558, 56584816, 56735576, 56917336, 57438404, 57594734, 57694224, 57704312, 58247118, 58447642, 58447816, 58523466, 58589880, 59161754, 59210784, 59305348, 59362002, 59405420, 59515830, 59692546, 59720358, 60133106, 60455792, 60540024, 60642326, 61030988, 61267078, 61837354, 62146946, 62276102, 63112418, 63165756, 63168480, 63823568, 64024604, 64476916, 64506894, 64568930, 64791668, 64911056, 65200798, 65305572, 65569854, 65791182, 271643232, 314187728, 399866798, … | (Folge | |
| 18 | 1, 24518, 40734, 145310, 361658, 525094, 676754, 773620, 1415198, 1488256, 1615588, 1828858, 2042774, 2514168, 2611294, 2676404, 3060772, 3547726, 3596074, 3673932, 3853792, 3933508, 4246258, 4489246, 5152128, 5205422, 5828034, 6287774, 6291332, 8521794, 8883864, 9125820, … | (Folge | |
| 19 | 1, 75898, 341112, 356926, 475856, 1880370, 2061748, 2312092, 2733014, 2788032, 2877652, 2985036, 3214654, 3638450, … | (Folge | |
| 20 | 1, 919444, 1059094, … | (Folge |
Stand: 10. Juni 2020
Die kleinsten
(mit
),
für die
erstmals eine Primzahl ergibt, kann man der obigen Tabelle entnehmen, was die
folgende Liste ergibt:
- 2, 2, 2, 2, 2, 30, 102, 120, 278, 46, 824, 150, 1534, 30406, 67234, 70906,
48594, 62722, 24518, 75898, 919444, … (Folge
 A056993 in OEIS)
A056993 in OEIS)
Die 10 größten bekannten verallgemeinerten Fermatschen Primzahlen
Der folgenden Liste kann man die 10 größten bekannten verallgemeinerten Fermatschen Primzahlen entnehmen. Sämtliche Entdecker dieser Primzahlen sind Teilnehmer des PrimeGrid-Projektes. In der zweiten Spalte steht, die wievieltgrößte bekannte Primzahl diese Fermatsche Primzahl im Moment ist.
| Rang | wievieltgrößte bekannte Primzahl(a) |
Primzahl | Fn(b) | Dezimalstellen von Fn(b) |
Entdeckungsdatum | Entdecker |
|---|---|---|---|---|---|---|
| 1 | 14. | 6.317.602 | 31. Oktober 2018 | Rob Gahan (IRL) | ||
| 2 | 15. | 6.253.210 | 29. August 2017 | Sylvanus A. Zimmerman (USA) | ||
| 3 | 36. | 3.439.810 | 31. Mai 2020 | Wolfgang Schwieger | ||
| 4 | 37. | 3.421.594 | 26. März 2020 | Ryan Propper | ||
| 5 | 38. | 3.411.613 | 24. Dezember 2019 | Alen Kecic (DEU) | ||
| 6 | 39. | 3.394.739 | 18. September 2019 | Peter Harvey (USA) | ||
| 7 | 40. | 3.386.397 | 29. Juni 2019 | Roman Vogt (DEU) | ||
| 8 | 41. | 3.379.193 | 17. April 2019 | Ed Goforth (NA) | ||
| 9 | 42. | 3.374.655 | 18. März 2019 | Yair Givoni (ISR) | ||
| 10 | 44. | 3.336.572 | 4. August 2018 | Rob Gahan (IRL) |
Die meisten der oben genannten Ergebnisse konnten natürlich nur mit Hilfe von Computern gefunden werden.
Literatur
- Solomon W. Golomb: On the sum of the reciprocals of the Fermat numbers and related irrationalities. In: Canad. J. Math. Vol. 15 (1963), S. 475–478.
- Florian Luca: The Anti-Social Fermat Number. In: American Mathematical Monthly. Vol. 107, Nr. 2 (Feb. 2000), S. 171–173.
- Aleksander Grytczuk, Florian Luca, Marek Wójtowicz: Another note on the greatest prime factors of Fermat numbers. In: Southeast Asian Bulletin of Mathematics. Vol. 25, Nr. 1 (Juli 2001), S. 111–115.
- Michal Křížek, Florian Luca, Lawrence Somer: 17 Lectures on Fermat Numbers: From Number Theory to Geometry. In: Canad. J. Math. S. 132–138.
- Fredrick Kennard: Unsolved Problems in Mathematics. S. 56.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 08.11. 2024