Heliumatom

Ein Heliumatom ist ein Atom des chemischen Elements Helium. Es ist zusammengesetzt aus zwei Elektronen, die durch die elektromagnetische Kraft an den Atomkern gebunden sind, der aus zwei Protonen und (je nach Isotop) einem oder zwei Neutronen besteht, die durch die starke Kraft zusammengehalten werden.

Anders als für Wasserstoff gibt es bislang keine geschlossene Lösung der Schrödingergleichung für das Heliumatom, d.h. die Energieniveaus lassen sich nicht exakt berechnen. Es gibt jedoch zahlreiche Näherungen, wie die Hartree-Fock-Methode, zum Abschätzen der Energieniveaus und der Wellenfunktion.

Eigenschaften der Atomhülle

Helium ist im Periodensystem das zweite und letzte Element der ersten Periode. Da innerhalb einer Periode die Atomradien mit zunehmender Elektronenzahl abnehmen und Wasserstoff und Helium die einzigen Elemente sind, in denen nur die erste Elektronenschale besetzt ist, hat Helium von allen Elementen den kleinsten Atomradius und die höchste Ionisierungsenergie.

Zwischen Heliumatomen wirken nur Van-der-Waals-Kräfte. Aufgrund der Kleinheit der Atome können die Elektronenhüllen nur sehr geringfügig polarisiert werden. Daher sind die ohnehin sehr schwachen Van-der-Waals-Kräfte im Fall von Helium besonders klein. Dies erklärt den extrem niedrigen Siedepunkt von 4,2 K (−268,8 °C).

Elektronenzustände

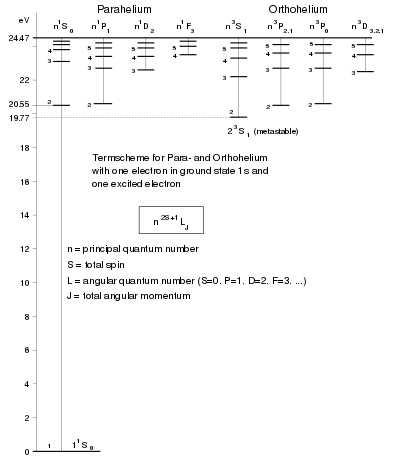
Ortho- und Parahelium

Im Grundzustand befinden sich die Elektronen im Zustand 1s², d.h. sie besetzen die beiden einzigen möglichen Zustände mit der Hauptquantenzahl 1 und dem Bahndrehimpuls 0. Die Spins der Elektronen sind antiparallel und addieren sich zum Gesamtspin S = 0 (Singulett-Zustand ¹S₀).

Der energetisch niedrigste Zustand mit S = 1 (Triplett-Zustand ³S₁) hat die Elektronenstruktur 1s2s und liegt um 19,8 eV darüber.

Zustände mit S = 0 nennt man Parahelium, solche mit S = 1 Orthohelium. Übergänge zwischen Ortho- und Parahelium sind stark unterdrückt („verboten“). Der niedrigste Orthohelium-Zustand ist daher vergleichsweise langlebig.

Quantenmechanische Beschreibung

Termschema für Para- and Orthohelium mit einem Elektron im Grundzustand 1s und einem angeregten Elektron.

Die quantenmechanische Beschreibung des Heliumatoms ist von besonderem Interesse, weil es das einfachste Mehrelektronenatom ist und auch zum Verständnis der Quantenverschränkung benutzt werden kann.

Der Hamiltonoperator für Helium, betrachtet als 3-Körper-System (bestehend aus zwei Elektronen und dem Kern), kann im Schwerpunktsystem geschrieben werden als

$H({\vec {r}}_{1},\,{\vec {r}}_{2})=\sum _{i=1,2}{\Bigg (}-{\frac {\hbar ^{2}}{2\mu }}\nabla _{r_{i}}^{2}-{\frac {Ze^{2}}{4\pi \varepsilon _{0}r_{i}}}{\Bigg )}-{\frac {\hbar ^{2}}{M}}\nabla _{r_{1}}\cdot \nabla _{r_{2}}+{\frac {e^{2}}{4\pi \varepsilon _{0}r_{12}}},$ /DD>

wobei die Elektronenmasse, die Kernmasse, $\mu ={\tfrac {mM}{m+M}}$ die reduzierte Masse eines Elektrons in Bezug auf den Kern, ${\vec {r}}_{1},\,{\vec {r}}_{2}$ die Elektron-Kern-Abstandsvektoren sind und $r_{12}=|{\vec {r_{1}}}-{\vec {r_{2}}}|$ ist. Die Kernladungszahl von Helium beträgt 2. In der Näherung eines unendlich schweren Kerns $M=\infty$ erhält man $\mu =m$ , und der Massen-Polarisations-Term ${\tfrac {\hbar ^{2}}{M}}\nabla _{r_{1}}\cdot \nabla _{r_{2}}$ verschwindet. In atomaren Einheiten vereinfacht sich der Hamiltonoperator zu

$H({\vec {r}}_{1},\,{\vec {r}}_{2})=-{\frac {1}{2}}\nabla _{r_{1}}^{2}-{\frac {1}{2}}\nabla _{r_{2}}^{2}-{\frac {Z}{r_{1}}}-{\frac {Z}{r_{2}}}+{\frac {1}{r_{12}}}.$

Es muss betont werden, dass der zugrundeliegende Raum nicht der gewöhnliche Raum, sondern ein 6-dimensionsionaler Konfigurationsraum $({\vec {r}}_{1},\,{\vec {r}}_{2})$ ist. In dieser Näherung (Pauli-Approximation) ist die Wellenfunktion ein Spinor zweiter Stufe mit 4 Komponenten $\psi _{ij}({\vec {r}}_{1},\,{\vec {r}}_{2})$ , wobei die Indizes $i,j=\,\uparrow ,\downarrow$ die Spin-Projektion der Elektronen im gewählten Koordinatensystem darstellen (-Richtung up oder down). Sie muss die übliche Normierungsbedingung $\sum _{ij}\int d{\vec {r}}_{1}d{\vec {r}}_{2}|\psi _{ij}|^{2}=1$ erfüllen. Dieser allgemeine Spinor kann als 2×2-Matrix ${\boldsymbol {\psi }}={\bigl (}{\begin{smallmatrix}\psi _{\uparrow \uparrow }&\psi _{\uparrow \downarrow }\\\psi _{\downarrow \uparrow }&\psi _{\downarrow \downarrow }\end{smallmatrix}}{\bigr )}$ dargestellt werden und folglich auch als Linearkombination einer beliebigen Basis von vier (im Vektorraum der 2×2-Matrizen) orthogonalen konstanten Matrizen ${\boldsymbol {\sigma }}_{k}^{i}$ mit skalaren Koeffizientenfunktionen $\phi _{i}^{k}({\vec {r}}_{1},\,{\vec {r}}_{2})$ als ${\boldsymbol {\psi }}=\sum _{ik}\phi _{i}^{k}({\vec {r}}_{1},\,{\vec {r}}_{2}){\boldsymbol {\sigma }}_{k}^{i}$ . Eine geeignete Basis wird gebildet aus einer antisymmetrischen Matrix (mit Gesamtspin $S=0$ , entsprechend einem Singulett-Zustand) ${\boldsymbol {\sigma }}_{0}^{0}={\tfrac {1}{\sqrt {2}}}{\bigl (}{\begin{smallmatrix}0&1\\-1&0\end{smallmatrix}}{\bigr )}={\tfrac {1}{\sqrt {2}}}(\uparrow \downarrow -\downarrow \uparrow )$ und drei symmetrischen Matrizen (mit Gesamtspin $S=1$ , entsprechend einem Triplett-Zustand) ${\boldsymbol {\sigma }}_{0}^{1}={\tfrac {1}{\sqrt {2}}}{\bigl (}{\begin{smallmatrix}0&1\\1&0\end{smallmatrix}}{\bigr )}={\tfrac {1}{\sqrt {2}}}(\uparrow \downarrow +\downarrow \uparrow )$ , ${\boldsymbol {\sigma }}_{1}^{1}={\bigl (}{\begin{smallmatrix}1&0\\0&0\end{smallmatrix}}{\bigr )}=\;\uparrow \uparrow ,$ ${\boldsymbol {\sigma }}_{-1}^{1}={\bigl (}{\begin{smallmatrix}0&0\\0&1\end{smallmatrix}}{\bigr )}=\;\downarrow \downarrow .$

Es ist leicht zu zeigen, dass der Singulett-Zustand invariant unter allen Drehungen ist (eine skalare Größe), während das Triplett auf einen gewöhnlichen Raumvektor $(\sigma _{x},\sigma _{y},\sigma _{z})$ mit den drei Komponenten $\sigma _{x}={\tfrac {1}{\sqrt {2}}}{\bigl (}{\begin{smallmatrix}1&0\\0&-1\end{smallmatrix}}{\bigr )}$ , $\sigma _{y}={\tfrac {i}{\sqrt {2}}}{\bigl (}{\begin{smallmatrix}1&0\\0&1\end{smallmatrix}}{\bigr )}$ und $\sigma _{z}={\tfrac {1}{\sqrt {2}}}{\bigl (}{\begin{smallmatrix}0&1\\1&0\end{smallmatrix}}{\bigr )}$ abgebildet werden kann.

Da im obigen (skalaren) Hamiltonian alle Spinwechselwirkungsterme zwischen den vier Komponenten von ${\boldsymbol {\psi }}$ vernachlässigt werden (z.B. ein externes Magnetfeld, oder relativistische Effekte wie Spin-Bahn-Wechselwirkungen), können die vier Schrödingergleichungen unabhängig voneinander gelöst werden.

Der Spin kommt hier nur ins Spiel durch das Pauli-Prinzip, das für Fermionen (wie Elektronen) die Antisymmetrie bei simultaner Vertauschung von Spin und Koordinaten fordert, also:

${\boldsymbol {\psi }}_{ij}({\vec {r}}_{1},\,{\vec {r}}_{2})=-{\boldsymbol {\psi }}_{ji}({\vec {r}}_{2},\,{\vec {r}}_{1})$

Parahelium ist damit der Singulett-Zustand ${\boldsymbol {\psi }}=\phi _{0}({\vec {r}}_{1},\,{\vec {r}}_{2}){\boldsymbol {\sigma }}_{0}^{0}$ mit einer symmetrischen Funktion $\phi _{0}({\vec {r}}_{1},\,{\vec {r}}_{2})=\phi _{0}({\vec {r}}_{2},\,{\vec {r}}_{1})$ und Orthohelium ist der Triplett-Zustand ${\boldsymbol {\psi }}_{m}=\phi _{1}({\vec {r}}_{1},\,{\vec {r}}_{2}){\boldsymbol {\sigma }}_{m}^{1},\;m=-1,0,1$ mit einer antisymmetrischen Funktion $\phi _{1}({\vec {r}}_{1},\,{\vec {r}}_{2})=-\phi _{1}({\vec {r}}_{2},\,{\vec {r}}_{1})$ . Wenn der Elektron-Elektron-Wechselwirkungsterm ignoriert wird (als erste Näherung), können beide Funktionen $\phi _{x},\;x=0,1$ als Linearkombinationen von zwei beliebigen (orthogonalen und normierten) Ein-Elektron-Eigenfunktionen $\varphi _{a},\varphi _{b}$ geschrieben werden: $\phi _{x}={\tfrac {1}{\sqrt {2}}}(\varphi _{a}({\vec {r}}_{1})\varphi _{b}({\vec {r}}_{2})\pm \varphi _{a}({\vec {r}}_{2})\varphi _{b}({\vec {r}}_{1}))$ oder für die Sonderfälle $\varphi _{a}=\varphi _{b}$ (beide Elektronen haben identische Quantenzahlen, nur für Parahelium): $\phi _{0}=\varphi _{a}({\vec {r}}_{1})\varphi _{a}({\vec {r}}_{2})$ . Die Gesamtenergie (als Eigenwert von ) ist dann in allen Fällen gleich $E=E_{a}+E_{b}$ (unabhängig von der Symmetrie).

Das erklärt das Fehlen des $1^{3}S_{1}$ -Zustands (mit $\varphi _{a}=\varphi _{b}=\varphi _{1s}$ ) für Orthohelium, wo folglich $2^{3}S_{1}$ (mit $\varphi _{a}=\varphi _{1s},\varphi _{b}=\varphi _{2s}$ ) der metastabile Grundzustand ist. (Ein Zustand mit den Quantenzahlen: Hauptquantenzahl , Gesamtspin , Drehimpulsquantenzahl und Gesamtdrehimpuls $J=|L-S|\dots L+S$ wird mit $n^{{2S+1}}L_{J}$ bezeichnet.)

Wenn der Elektron-Elektron-Wechselwirkungsterm ${\tfrac {1}{r_{12}}}$ einbezogen wird, ist die Schrödingergleichung nicht separabel. Aber auch dann, wenn er vernachlässigt wird, können alle oben beschriebenen Zustände (sogar mit zwei identischen Quantenzahlen, wie $1^{1}S_{0}$ mit ${\boldsymbol {\psi }}=\varphi _{1s}({\vec {r}}_{1})\varphi _{1s}({\vec {r}}_{2}){\boldsymbol {\sigma }}_{0}^{0}$ ) nicht als Produkt von Ein-Elektron-Wellenfunktionen geschrieben werden: $\psi _{ik}({\vec {r}}_{1},\,{\vec {r}}_{2})\neq \chi _{i}({\vec {r}}_{1})\xi _{k}({\vec {r}}_{2})$ – die Wellenfunktion ist verschränkt. Man kann nicht sagen, Teilchen 1 ist in Zustand 1 und das andere in Zustand 2; und man kann keine Messungen an einem Teilchen ausführen, ohne das andere zu beeinflussen.

Siehe auch

Ortho- und Parawasserstoff

Basierend auf einem Artikel in:

Wikipedia.de