Hartree-Fock-Methode

Unter Hartree-Fock-Rechnung (beziehungsweise Hartree-Fock-Methode, nach Douglas Rayner Hartree und Wladimir Alexandrowitsch Fock) versteht man eine Methode der Quantenmechanik, in der Systeme mit mehreren gleichartigen Teilchen in Mean-Field-Näherung behandelt werden. Sie wird zum Beispiel verwendet in der Atomphysik, der Theoretischen Chemie zur Beschreibung von Elektronen in Molekülen und der Kernphysik für Systeme aus Protonen und Neutronen.

Sie ermöglicht es, Orbitalenergien und Wellenfunktionen von quantenmechanischen Vielteilchensystemen näherungsweise zu berechnen und ist eine so genannte Ab-initio-Methode, d.h. sie kommt ohne empirische Parameter aus und benötigt nur Naturkonstanten. Sie ist der Ausgangspunkt für Post-Hartree-Fock-Methoden, welche die Genauigkeit der Berechnungen verbessern.

Die Hartree-Fock-Methode ist die Basis der Molekülorbitaltheorie.

Funktionsweise

Die Hartree-Fock-Methode geht von der zeitunabhängigen Schrödinger-Gleichung (hier in Dirac-Notation)

${\hat {H}}\,|\psi \rangle =E\,|\psi \rangle$

aus, welche die Energie eines Systems aus der Wellenfunktion $|\psi \rangle$ berechnet, indem die Eigenwerte des Hamilton-Operators ${\hat {H}}$ zu dieser Wellenfunktion gesucht werden. Im Hamilton-Operator werden alle Energiebeiträge der Teilchen und Felder im System sowie deren Wechselwirkungen untereinander beschrieben. In vielen praktisch wichtigen Systemen (wie z.B. den Elektronen in einem Molekül) sind die Teilchen miteinander korreliert und beeinflussen sich gegenseitig. Dadurch kann die Schrödinger-Gleichung für solche Systeme nicht mehr exakt, sondern nur noch näherungsweise gelöst werden.

Die Hartree-Fock-Methode vereinfacht die Wechselwirkungen der Teilchen untereinander so, dass diese nicht mehr jeweils paarweise untereinander wechselwirken, sondern mit einem Feld, das von allen anderen Teilchen im Mittelwert erzeugt wird – dem so genannten mean field (mittleren Feld). Das Feld hängt zwar immer noch vom Verhalten der einzelnen Teilchen ab, die Lösung kann aber jetzt schrittweise berechnet werden:

Ein Ausgangszustand wird ausgewählt und daraus das Feld erzeugt.
Mit diesem wird dann die Schrödingergleichung für jedes einzelne Teilchen gelöst.
Zusammengenommen ergeben die einzelnen Lösungen dann einen neuen Zustand und ein neues Feld.

Dieser Vorgang wird wiederholt, bis sich aufeinanderfolgende Lösungen nur mehr geringfügig unterscheiden, das Feld also zu Lösungen führt, die das Feld selbst konsistent wieder erzeugen. Daraus leitet sich der Begriff self-consistent field ab, der für diesen Teil der Hartree-Fock-Methode verwendet wird.

Als Wellenfunktionen für die behandelten Vielteilchensysteme werden bei Bosonen ein symmetrisches (Hartree-)Produkt von Einteilchenwellenfunktionen verwendet, bei Fermionen (wie Elektronen, Protonen und Neutronen) eine antisymmetrische Kombination dieser Produkte (eine sogenannte Slater-Determinante). Um die Schrödingergleichung zu lösen, werden diese Einteilchenwellenfunktionen so variiert, dass die aus der Gleichung entstehende Energie minimal wird. Aufgrund des Rayleigh-Ritz-Prinzips ist diese Energie dann eine obere Grenze für die tatsächliche Energie des Systems. Die dadurch berechnete Wellenfunktion des gesamten Systems ist allerdings nicht notwendigerweise eine Annäherung der tatsächlichen Wellenfunktion.

Bei manchen Molekülen (insbesondere mit ungepaarten Elektronen) wird statt einer einzigen Slater-Determinante eine symmetrieadaptierte Linearkombination mehrerer Slater-Determinanten angesetzt, deren Koeffizienten aber durch die (Spin-)Symmetrie des Systems festgelegt sind.

Hartree-Fock-Gleichung

Die Hartree-Fock-Gleichung ist ein nichtlineares Eigenwertproblem mit einem nichtlokalen Integrodifferentialoperator. Sie lautet in Dirac-Notation

${\hat {F}}|\phi _{m}\rangle =\varepsilon _{m}|\phi _{m}\rangle \,\!$

mit dem Fock-Operator ${\hat {F}}$

${\hat {F}}={\hat {h}}+\sum \limits _{\gamma }^{N}\left(\left\langle \phi _{\gamma }\right|{\hat {w}}\left|\phi _{\gamma }\right\rangle -\left|\phi _{\gamma }\right\rangle \left\langle \phi _{\gamma }\right|{\hat {w}}\right)$

${\text{mit: }}{\hat {h}}=-{\frac {\Delta ({\mathbf {r}})}{2}}-\sum \limits _{k}^{{N_{k}}}{\frac {Z_{k}}{\left|{{\mathbf {r}}-{\mathbf {R_{k}}}}\right|}}\qquad {\text{ und }}\qquad {\hat {w}}={\frac {1}{\left|{{\mathbf {r_{1}}}-{\mathbf {r_{2}}}}\right|}}$

wobei ${\hat {h}}$ der Einteilchenanteil des Hamiltonoperators ist und ${\hat {w}}$ der Anteil der Zweiteilchenwechselwirkung, wie oben erwähnt für den Spezialfall der Molekülphysik von Elektronen mit Coulombwechselwirkung untereinander und in atomaren Einheiten.

Der Index $\gamma$ läuft hierbei über die besetzten elektronischen Zustände, also die mit den niedrigsten Eigenwerten, wobei die Zahl der Elektronen angibt. Der Index läuft über die Atomkerne, wobei $N_{k}$ die Anzahl der Kerne angibt.

Matrixdarstellung

Um effiziente Lösungsmethoden verwenden zu können, wird die Gleichung zusätzlich in eine Matrixdarstellung übergeführt, indem man $|\phi _{m}\rangle$ in der Basis $|\varphi_i\rangle$ darstellt, sodass $|\phi _{m}\rangle =\sum \limits _{i}^{n}c_{{im}}|\varphi _{i}\rangle$ . Diese Basis ist typischerweise nicht orthogonal.

$\sum \limits _{i}{\hat {F}}c_{{im}}|\varphi _{i}\rangle =\varepsilon _{m}\sum \limits _{i}c_{{im}}|\varphi _{i}\rangle$

Nach Multiplikation mit $\langle \varphi _{j}|$ ergibt sich das verallgemeinerte Eigenwertproblem

$\sum \limits _{i}\langle \varphi _{j}|{\hat {F}}|\varphi _{i}\rangle c_{{im}}=\varepsilon _{m}\sum \limits _{i}\langle \varphi _{j}|\varphi _{i}\rangle c_{{im}}$

$F{\mathbf {c}}_{m}=\varepsilon _{m}S{\mathbf {c}}_{m}\,\!$

mit der Fockmatrix $F_{{ji}}=\langle \varphi _{j}|{\hat {F}}|\varphi _{i}\rangle$ , der Überlappmatrix $S_{{ji}}=\langle \varphi _{j}|\varphi _{i}\rangle$ und den Koeffizientenvektoren ${\mathbf {c}}_{{m}}$ . Diese Gleichung ist auch als Roothaan-Hall-Gleichung bekannt. Wird die Basis diagonalisiert (z.B. mit Löwdins symmetrischer Orthogonalisierung), wodurch die Überlappmatrix zu einer Einheitsmatrix wird, vereinfacht sich die Gleichung zu einem einfachen Eingenwertproblem, das von Computern effizient gelöst werden kann.

Als Lösung erhält man Eigenwerte und Eigenvektoren, wovon man die niedrigsten Eigenwerte und zugehörigen Eigenvektoren als besetzte Zustände ansieht. Als Basisfunktionen kommen in vielen Fällen Linearkombinationen von Gaussian Type Orbitals (GTO) oder Slater Type Orbitals (STO) zum Einsatz. Für Berechnungen an einzelnen Atomen und zweiatomigen oder linearen Molekülen können die Hartree-Fock-Gleichungen auch mit numerischen Verfahren gelöst werden.

Spin

Um die Hartree-Fock-Gleichung zu lösen, muss von den oben verwendeten Spinorbitalen $\left|\phi _{m}\right\rangle$ noch die Spinwellenfunktion $\left|\chi _{m}\right\rangle$ abgespalten werden, sodass $\left|\phi _{m}\right\rangle =\left|\psi _{m}\right\rangle \left|\chi _{m}\right\rangle$ mit der reinen Ortswellenfunktion $\left|\psi _{m}\right\rangle$ gilt.

Geschlossene-Schalen-Hartree-Fock (RHF)

Bei dem Geschlossene-Schalen-Hartree-Fock Ansatz (engl. Restricted Hartree Fock) werden alle Spins als gepaart angenommen, was natürlich nur bei einer geraden Anzahl von Elektronen möglich ist. Der Grundzustand wird somit als Spin-Singulett angenommen. Für die Wellenfunktionen folgt somit

$\left|\phi _{1}\right\rangle =\left|\psi _{1}\right\rangle \left|\alpha \right\rangle ,\;\left|\phi _{2}\right\rangle =\left|\psi _{1}\right\rangle \left|\beta \right\rangle ,\;\left|\phi _{3}\right\rangle =\left|\psi _{2}\right\rangle \left|\alpha \right\rangle ,\dots ,\left|\phi _{N}\right\rangle =\left|\psi _{{N/2}}\right\rangle \left|\beta \right\rangle .$

${\text{mit }}{\hat {s}}_{z}\left|\alpha \right\rangle ={\frac {1}{2}}\left|\alpha \right\rangle {\text{ und }}{\hat {s}}_{z}\left|\beta \right\rangle =-{\frac {1}{2}}\left|\beta \right\rangle$

Setzt man dies in die Hartree-Fock-Gleichung ein, folgt

${\hat {F}}_{{{\text{RHF}}}}\left|\psi _{m}\right\rangle ={\hat {h}}\left|\psi _{m}\right\rangle +\sum \limits _{{\gamma }}^{{N/2}}2\left\langle \psi _{\gamma }\right|{\hat {w}}\left|\psi _{\gamma }\right\rangle \left|\psi _{m}\right\rangle -\left\langle \psi _{\gamma }\right|{\hat {w}}\left|\psi _{m}\right\rangle \left|\psi _{\gamma }\right\rangle =\varepsilon _{m}\left|\psi _{m}\right\rangle .$

Die Coulombwechselwirkung tritt somit zwischen allen Elektronen auf, die Austauschwechselwirkung hingegen nur zwischen Elektronen mit gleichem Spin. Wegen der Symmetrie zwischen Spin up und down ist die HF-Gleichung für beide Spinkonfigurationen gleich, sodass weiterhin nur eine Eigenwertgleichung gelöst werden muss, wobei nun allerdings nur noch die niedrigsten N/2 Eigenwerte und Eigenvektoren verwendet werden müssen.

Offene-Schalen-Hartree-Fock (UHF)

Bei dem Offene-Schalen-Hartree-Fock-Ansatz (engl. Unrestricted Hartree Fock) wird im Vergleich zum Geschlossene-Schalen-Ansatz (RHF) die Forderung fallengelassen, dass gleich viele Elektronen im Zustand $\left|\alpha \right\rangle$ , wie im Zustand $\left|\beta \right\rangle$ sein müssen. Die Spinorbitale werden demnach angesetzt als

$\left|\phi _{1}\right\rangle =\left|\psi _{1}^{\alpha }\right\rangle \left|\alpha \right\rangle ,\;\left|\phi _{2}\right\rangle =\left|\psi _{2}^{\alpha }\right\rangle \left|\alpha \right\rangle ,\dots ,\left|\phi _{{N_{\alpha }}}\right\rangle =\left|\psi _{{N_{\alpha }}}^{\alpha }\right\rangle \left|\alpha \right\rangle ,\;\left|\phi _{{N_{\alpha }+1}}\right\rangle =\left|\psi _{1}^{\beta }\right\rangle \left|\beta \right\rangle ,\dots ,\left|\phi _{{N}}\right\rangle =\left|\psi _{{N_{\beta }}}^{\beta }\right\rangle \left|\beta \right\rangle .$

Nach Einsetzen in die ursprüngliche Hartree-Fock-Gleichung ergeben sich zwei verschiedene Gleichungen für $\left|\alpha \right\rangle$ und $\left|\beta \right\rangle$ .

${\hat {F}}_{{{\text{UHF}}}}^{\alpha }\left|\psi _{m}^{\alpha }\right\rangle ={\hat {h}}\left|\psi _{m}^{\alpha }\right\rangle +\sum \limits _{{\gamma }}^{{N_{\alpha }}}\left\langle \psi _{\gamma }^{\alpha }\right|{\hat {w}}\left|\psi _{\gamma }^{\alpha }\right\rangle \left|\psi _{m}^{\alpha }\right\rangle -\left\langle \psi _{\gamma }^{\alpha }\right|{\hat {w}}\left|\psi _{m}^{\alpha }\right\rangle \left|\psi _{\gamma }^{\alpha }\right\rangle +\sum \limits _{{\gamma }}^{{N_{\beta }}}\left\langle \psi _{\gamma }^{\beta }\right|{\hat {w}}\left|\psi _{\gamma }^{\beta }\right\rangle \left|\psi _{m}^{\alpha }\right\rangle =\varepsilon _{m}\left|\psi _{m}^{\alpha }\right\rangle .$

Die Gleichung für $\left|\beta \right\rangle$ folgt aus der Ersetzung $\alpha \rightarrow \beta$ und $\beta \rightarrow \alpha$ . Hierbei sieht man wieder, dass Elektronen mit gleichem Spin Coulomb- und Austauschwechselwirkung besitzen, Elektronen mit unterschiedlichem Spin wechselwirken hingegen nur über den Coulombterm. Da die Austauschwechselwirkung die Gesamtenergie stets verringert, kann somit, im Rahmen von Hartree-Fock, die zweite Hundsche Regel erklärt werden. Diese besagt, dass bei sonstiger Entartung oder Quasientartung die Spins zweier Elektronen möglichst parallel ausgerichtet sind.

Herleitung für Fermionen

Zur Herleitung der Hartree-Fock Gleichungen geht man zunächst von der stationären Schrödingergleichung aus. Hier wird der Spezialfall eines Hamiltonoperators mit Coulombwechselwirkung in der Born-Oppenheimer-Näherung betrachtet, wie er zum Beispiel für Elektronen in der Molekülphysik auftritt. Das heißt

${\hat {H}}=\sum \limits _{{i}}^{{N}}\underbrace {\left(-{\frac {\Delta ({\mathbf {r}}_{i})}{2}}-\sum \limits _{k}^{{N_{k}}}{\frac {Z_{k}}{\left|{{\mathbf {r_{i}}}-{\mathbf {R_{k}}}}\right|}}\right)}_{{{\hat {h}}_{i}}}+{\frac {1}{2}}\sum \limits _{{i}}^{{N}}\sum \limits _{{j\neq i}}^{{N}}\underbrace {{\frac {1}{\left|{{\mathbf {r_{i}}}-{\mathbf {r_{j}}}}\right|}}}_{{{\hat {w}}_{{ij}}}}$

$\mathbf {r}$ bezeichnet hierbei die elektronischen Koordinaten, die Anzahl der Elektronen, $Z_{k}$ und ${\mathbf {R}}_{k}$ die Ladung und festen Koordinaten der Kerne. ${\hat {h}}_{i}$ ist nun ein Einteilchenoperator und besteht aus der kinetischen Energie und der Wechselwirkung mit allen Kernen des -ten Elektrons. ${\hat {w}}_{{ij}}$ ist hingegen ein Zweiteilchenoperator und stellt die Coulombwechselwirkung des -ten mit dem -ten Elektron dar. Die stationäre Schrödingergleichung lautet nun

${\hat {H}}\left|\Psi \right\rangle =E\left|\Psi \right\rangle$

Als Näherung für Hartree-Fock schreibt man nun $\left|\Psi \right\rangle$ als Slater-Determinante von Einteilchenwellenfunktionen $\left|\phi _{i}\right\rangle$ . Die Näherung besteht darin, dass man für die exakte Lösung über alle möglichen Slater-Determinanten summieren müsste, z.B. indem man $\phi _{N}$ durch $\phi _{{N+1}}$ ersetzt. Somit gilt

$\left|\Psi \right\rangle \approx {\frac {1}{{\sqrt {N!}}}}{\begin{vmatrix}\phi _{1}(1)&\phi _{2}(1)&\dots &\phi _{N}(1)\\\phi _{1}(2)&\phi _{2}(2)&\dots &\phi _{N}(2)\\\vdots &\vdots &\ddots &\vdots \\\phi _{1}(N)&\phi _{2}(N)&\dots &\phi _{N}(N)\end{vmatrix}}$

und die Energie des Systems lautet

$E=\left\langle \Psi \right|{\hat {H}}\left|\Psi \right\rangle$

Dies kann man nun, indem man die Orthogonalität der $\phi _{i}$ ausnutzt, zu

$E[\{\phi _{i}\}]=\sum \limits _{{\alpha }}^{{N}}\int \phi _{\alpha }^{*}({\mathbf {r}}_{i}){\hat {h}}_{i}\phi _{\alpha }({\mathbf {r}}_{i})\,{\mathrm {d^{3}}}{\mathbf {r}}_{i}+{\frac {1}{2}}\sum \limits _{\alpha }^{N}\sum \limits _{{\gamma \neq \alpha }}^{N}\left(\iint \phi _{\alpha }^{*}({\mathbf {r}}_{i})\phi _{\gamma }^{*}({\mathbf {r}}_{j}){\hat {w}}_{{ij}}\,\phi _{\gamma }({\mathbf {r}}_{j})\phi _{\alpha }({\mathbf {r}}_{i})\,d^{3}{\mathbf {r}}_{i}\,d^{3}{\mathbf {r}}_{j}\right.$

$\quad -\left.\iint \phi _{\alpha }^{*}({\mathbf {r}}_{i})\phi _{\gamma }^{*}({\mathbf {r}}_{j}){\hat {w}}_{{ij}}\,\phi _{\gamma }({\mathbf {r}}_{i})\phi _{\alpha }({\mathbf {r}}_{j})\,d^{3}{\mathbf {r}}_{i}\,d^{3}{\mathbf {r}}_{j}\right)$

$=\sum \limits _{{\alpha }}^{{N}}\left\langle \phi _{\alpha }\right|{\hat {h}}\left|\phi _{\alpha }\right\rangle +{\frac {1}{2}}\sum \limits _{\alpha }^{N}\sum \limits _{{\gamma \neq \alpha }}^{N}\left(\left\langle \phi _{\alpha }\phi _{\gamma }\right|{\hat {w}}\left|\phi _{\gamma }\phi _{\alpha }\right\rangle -\left\langle \phi _{\alpha }\phi _{\gamma }\right|{\hat {w}}\left|\phi _{\alpha }\phi _{\gamma }\right\rangle \right)$

umformen. Nun wird das Ritzsche Variationsprinzip verwendet und als Funktional nach $\phi _{i}$ variiert. Um die Orthogonalität der Einteilchenfunktionen zu erhalten wird allerdings nicht direkt minimiert, sondern nach der Methode der Lagrange-Multiplikatoren das Funktional ${\mathcal {L}}$

${\mathcal {L}}=E[\{\phi _{i}\}]-\sum \limits _{i}^{N}\sum \limits _{{j}}^{N}\varepsilon _{{ij}}\left(\delta _{{ij}}-\left\langle \phi _{i}\right|\left.\phi _{j}\right\rangle \ \right).$

Man kann nun in die Basis ${\tilde {\phi }}_{i}$ wechseln, in der $\varepsilon _{{ij}}$ diagonal ist, also $\varepsilon _{{ij}}=\varepsilon _{i}\delta _{{ij}}$ .

${\mathcal {L}}=E[\{{\tilde {\phi }}_{i}\}]-\sum \limits _{i}^{N}\varepsilon _{{i}}\left(1-\left\langle {\tilde {\phi }}_{i}\right|\left.{\tilde {\phi }}_{i}\right\rangle \right)$

Die Tilde wird im Weiteren weggelassen. Nun kann ${\mathcal {L}}$ bezüglich $\phi _{m}$ minimiert werden.

${\frac {\partial {\mathcal {L}}}{\partial \phi _{m}^{*}}}={\frac {\partial }{\partial \phi _{m}^{*}}}\left\{\sum \limits _{\alpha }^{N}\left\langle \phi _{\alpha }\right|{\hat {h}}\left|\phi _{\alpha }\right\rangle +{\frac {1}{2}}\sum \limits _{\alpha }^{N}\sum \limits _{\gamma \neq \alpha }^{N}\left(\left\langle \phi _{\alpha }\phi _{\gamma }\right|{\hat {w}}\left|\phi _{\gamma }\phi _{\alpha }\right\rangle -\left\langle \phi _{\alpha }\phi _{\gamma }\right|{\hat {w}}\left|\phi _{\alpha }\phi _{\gamma }\right\rangle \right)-\sum \limits _{i}^{N}\varepsilon _{i}\left(1-\left\langle \phi _{i}\right|\left.\phi _{i}\right\rangle \ \right)\right\}$

$={\hat {h}}\left|\phi _{m}\right\rangle +\sum \limits _{{\gamma \neq m}}^{{N}}\int \phi _{\gamma }^{*}({\mathbf {r}}_{1}){\hat {w}}_{{12}}\phi _{\gamma }({\mathbf {r}}_{1})\phi _{m}({\mathbf {r}}_{2})\,{\mathrm {d^{3}}}{\mathbf {r}}_{1}-\int \phi _{\gamma }^{*}({\mathbf {r}}_{1}){\hat {w}}_{{12}}\phi _{m}({\mathbf {r}}_{1})\phi _{\gamma }({\mathbf {r}}_{2})\,{\mathrm {d^{3}}}{\mathbf {r}}_{1}-\varepsilon _{m}\left|\phi _{m}\right\rangle$

$={\hat {h}}\left|\phi _{m}\right\rangle +\sum \limits _{{\gamma \neq m}}^{{N}}\underbrace {\left\langle \phi _{\gamma }\right|{\hat {w}}\left|\phi _{\gamma }\right\rangle \left|\phi _{m}\right\rangle }_{{{\text{Coulomb-WW.}}}}-\underbrace {\left\langle \phi _{\gamma }\right|{\hat {w}}\left|\phi _{m}\right\rangle \left|\phi _{\gamma }\right\rangle }_{{{\text{Austausch-WW.}}}}-\varepsilon _{m}\left|\phi _{m}\right\rangle$

Da der Summand mit $\gamma =m$ gleich Null ist, kann er hinzugenommen werden, wodurch alle Gleichungen identisch sind und somit der Index weggelassen werden kann.

$={\hat {h}}\left|\phi _{m}\right\rangle +\sum \limits _{{\gamma }}^{{N}}\left\langle \phi _{\gamma }\right|{\hat {w}}\left|\phi _{\gamma }\right\rangle \left|\phi _{m}\right\rangle -\left\langle \phi _{\gamma }\right|{\hat {w}}\left|\phi _{m}\right\rangle \left|\phi _{\gamma }\right\rangle -\varepsilon _{m}\left|\phi _{m}\right\rangle =0$

Somit folgt

${\hat {F}}\left|\phi _{m}\right\rangle ={\hat {h}}\left|\phi _{m}\right\rangle +\sum \limits _{{\gamma }}^{{N}}\left(\left\langle \phi _{\gamma }\right|{\hat {w}}\left|\phi _{\gamma }\right\rangle \left|\phi _{m}\right\rangle -\left\langle \phi _{\gamma }\right|{\hat {w}}\left|\phi _{m}\right\rangle \left|\phi _{\gamma }\right\rangle \right)=\varepsilon _{m}\left|\phi _{m}\right\rangle ,$

die Hartree-Fock-Gleichung mit dem Fock-Operator ${\hat {F}}$ . Hierbei besitzen die beiden ersten Terme ein klassisches Analogon. ${\hat {h}}$ enthält die kinetische Energie und die Coulombwechselwirkung mit den Kernen. Der zweite Term kann als mittleres Coulombpotential aller anderen Elektronen auf das -te Elektron interpretiert werden. Die instantane Korrelation der Teilchen wird jedoch vernachlässigt. Die Hartree-Fock-Methode ist daher ein Mean-Field-Ansatz. Der Austauschterm besitzt kein klassisches Analagon. Der Fockoperator für das -te Elektron enthält die Wellenfunktionen aller anderer Elektronen, wodurch die Fockgleichungen meist nur mit der Methode der selbstkonsistenten Felder, d.h. iterativ mittels Fixpunktiteration, gelöst werden kann. Zur Konvergenzbeschleunigung kommt hierzu häufig das DIIS-Verfahren zum Einsatz.

Basissätze

→ Hauptartikel: Basissatz (Chemie)

Darstellung verschiedener STO-NG-Orbitale und das zugehörige ursprüngliche STO-Orbital

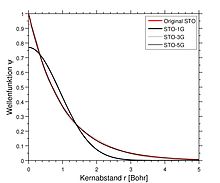
Eine direkte numerische Lösung der Hartree-Fock-Gleichung als Differentialgleichung ist bei Atomen und linearen Molekülen möglich. In der Regel werden die Orbitale aber analytisch als Linearkombinationen von Basisfunktionen angesetzt (Basissatz), was wiederum eine Näherung darstellt, die umso besser wird, je größer und intelligenter der Basissatz gewählt wird. Typischerweise bringt jedes Atom im Molekül nun eine vom entsprechenden Basissatz festgelegte Anzahl von Basisfunktionen, die auf ihm zentriert sind, mit. Als grober Ausgangspunkt zur Erstellung solcher Basissätze dienen die analytischen Lösungen des Wasserstoffatoms, welche ein $\exp(-\zeta r)$ -Verhalten für große Kernabstände zeigen. Ansätze dieses Typs nennt man Slater Type Orbital (STO). Meist haben sie die Form

$\left|\varphi _{i}^{k}\right\rangle ={\text{Polynom}}\cdot \exp \left(-\zeta _{i}\left|{\mathbf {r}}-{\mathbf {R_{k}}}\right|\right)$ .

Ein $p_{z}$ -Orbital besitzt z.B. die Form

$\left|\varphi _{i}^{k}\right\rangle =(z-z_{k})\cdot \exp \left(-\zeta _{i}\left|{\mathbf {r}}-{\mathbf {R_{k}}}\right|\right)$ .

Der große Nachteil der Slater-Type-Orbitale ist jedoch, dass die erforderlichen Matrixelemente $\left\langle \varphi _{\tau }\left|\langle \varphi _{\nu }\left|{\hat {w}}\right|\varphi _{\eta }\rangle \right|\varphi _{\gamma }\right\rangle$ nicht im Allgemeinen analytisch berechenbar sind. Deshalb benutzt man fast ausschließlich Gaussian Type Orbitals, d.h. Basisfunktion der Form

$\left|\varphi _{i}^{k}\right\rangle ={\text{Polynom}}\cdot \exp \left(-\zeta _{i}({\mathbf {r}}-{\mathbf {R_{k}}})^{2}\right)$ .

Hierbei können die Matrixelemente analytisch berechnet werden. Dabei wird u.a. das Gaussian Product Theorem ausgenutzt, d.h., dass das Produkt zweier Gaußfunktionen wieder eine Gaußfunktion ist. Um die STOs besser zu approximieren, besteht typischerweise eine Basisfunktion aus mehreren Gaußfunktionen mit festen, vom Basissatz festgelegten Parametern („Contraction“). Ein einfacher Basissatz ist z.B. der sog. STO-NG, welcher Slater Type Orbitale mit Gaußfunktionen annähert. Damit wird die Lösung der Differentialgleichung reduziert auf die analytische Berechnung von Integralen über diese Basisfunktionen und die iterative Lösung des verallgemeinerten Eigenwertproblems mit den Koeffizienten der Basisfunktionen als zu bestimmende Parameter.

Häufig verwendete Basissätze sind die Pople- und die korrelationskonsistenten Basen.

Vor- und Nachteile

Die mit der Hartree-Fock-Methode errechnete Energie erreicht nie den exakten Wert, selbst wenn ein unendlich großer Basissatz verwendet werden würde. Bei diesem Grenzfall wird das sogenannte Hartree-Fock-Limit erreicht. Der Grund dafür ist, dass durch die Verwendung des gemittelten Potenzials die Elektronenkorrelation, also die genaue Wechselwirkung der Elektronen untereinander, nicht erfasst wird. Um diesen Makel zu beseitigen, wurden Methoden entwickelt, die in der Lage sind, zumindest einen Teil der Elektronenkorrelation zu erfassen. Von Bedeutung sind insbesondere Coupled-Cluster-Methoden und die Møller-Plesset-Störungstheorie, die auf der Lösung des Hartree-Fock-Verfahrens aufbauen. Eine andere sehr bedeutende Methode ist die Dichtefunktionaltheorie mit Hybridfunktionalen, bei der der Hartree-Fock-Austausch anteilig in den Austausch-Korrelations-Teil des Dichtefunktionals eingeht.

Die Hartree-Fock-Methode erlaubt aber bei sehr vielen Molekülen eine gute Bestimmung ihrer „groben“ elektronischen Struktur. Daher können z. B. die Molekülorbitale für qualitative Betrachtungen herangezogen werden (z. B. im Falle von Grenzorbitalen). Die Hartree-Fock Methode liefert im Regelfall elektronische Gesamtenergien, die bis auf 0,5 % mit den korrekten elektronischen Energien übereinstimmen (zur Berechnung von Energiedifferenzen, wie z.B. Reaktionsenergien, ist sie aber nur sehr bedingt brauchbar, da diese in der Größenordnung des Fehlers liegen), Dipolmomente, die auf 20 % mit den wirklichen Dipolmomenten übereinstimmen, und sehr genaue Verteilungen der Elektronendichte im Molekül. Aufgrund dieser Eigenschaften werden Hartree-Fock-Rechnungen häufig als Ausgangspunkt für die oben genannten genaueren Rechnungen verwendet.

Ein weiterer Vorteil der Hartree-Fock-Methode ist, dass die erhaltene Energie gemäß dem Variationsprinzip eine obere Schranke für die exakte Grundzustandsenergie darstellt. Durch die Wahl umfangreicherer Basissätze kann die berechnete Wellenfunktion systematisch bis zum sogenannten "Hartree-Fock Limit" verbessert werden. Eine derartige systematische Betrachtungsweise ist bei Dichtefunktionalmethoden nicht möglich.

Literatur

Joachim Reinhold: Quantentheorie der Moleküle. Teubner, Wiesbaden 2006, ISBN 3-8351-0037-8.
Frank Jensen: Introduction to Computational Chemistry. 2. Auflage. Wiley, Chichester 2007, ISBN 978-0-470-01187-4.

Basierend auf einem Artikel in:

Wikipedia.de