Basissatz (Chemie)

Als Basissatz wird in der theoretischen und der Computerchemie ein Satz an Funktionen (den sogenannten Basisfunktionen) bezeichnet, der dafür genutzt wird die elektronische Wellenfunktion in Hartree-Fock-Methoden oder der Dichtefunktionaltheorie zu repräsentieren um die partiellen Differentialgleichungen des Modells in algebraische Gleichungen zu wandeln, die für effiziente Implementierungen auf einem Computer sinnvoll sind.

Die Nutzung von Basissätzen ist äquivalent zur Nutzung einer angenäherten Lösung der Identität. Die Einteilchenzustände (Molekülorbitale) werden dann in Form von Linearkombinationen der Basisfunktionen ausgedrückt.

Der Basissatz kann entweder aus Atomorbitalen (was zum Ansatz der LCAO-Methode führt) oder ebenen Wellen zusammengesetzt sein. Ersterer Ansatz wird primär von Quantenchemikern genutzt, während letzterer typischerweise von Festkörperforschern genutzt wird. Grundsätzlich können verschiedene Arten von Atomorbitalen genutzt werden: Gaussian Type Orbitals, Slater Type Orbitals oder numerische Atomorbitale. Am häufigsten von diesen dreien werden die Gaussian Type Orbitals genutzt, da sie effiziente Implementierungen von Post-Hartree-Fock-Methoden erlauben.

Einführung

In der modernen Computerchemie werden quantenchemische Rechnungen mit einem endlichen Satz an Basisfunktionen ausgeführt. Wenn dieser endliche Satz in Richtung eines (unendlichen) vollständigen Satzes an Funktionen erweitert wird, wird das als Näherung an das complete basis set (CBS, deutsch: gesamter Basissatz) Limit bezeichnet. In diesem Artikel werden Basisfunktion und Atomorbital austauschbar verwendet, obwohl es sich bei den Basisfunktionen normalerweise nicht um echte Atomorbitale handelt, da viele Basisfunktionen genutzt werden, um Polarisationseffekte in Molekülen zu beschreiben.

Innerhalb eines Basissatzes wird die Wellenfunktion als Vektor repräsentiert, die Bestandteile von diesem korrespondieren mit den Koeffizienten der Basisfunktion in der linearen Verlängerung. In einer solchen Basis korrespondieren Einelektronenoperatoren wiederum zu Matrizen (auch als Tensor der Stufe 2 bezeichnet), wohingegen es sich bei Zweielektronenoperatoren um Tensoren der Stufe 4 handelt.

Wenn molekulare Rechnungen ausgeführt werden, ist es üblich, eine Basis aus Atomorbitalen zu nutzen, die auf die Kerne innerhalb des Moleküls zentriert ist (LCAO-Methode). Die physikalisch besten Basissätze sind Slater Type Orbitals (STOs), die Lösungen der Schrödingergleichung von wasserstoffartigen Atomen sind und exponentiell mit der Entfernung zum Kern abnehmen. Es kann dabei gezeigt werden, dass die Molekülorbitale von Hartree-Fock und Dichtefunktionaltheorie ebenfalls exponential abnehmen. Außerdem erfüllen S-artige STOs Katos Theorem am Kern, was bedeutet, dass sie dazu in der Lage sind die Elektronendichte nahe dem Kern akkurat zu beschreiben. Trotzdem fehlen wasserstoffartigen Atomen viele Mehrelektroneninteraktionen, da die Orbitale die elektronische Korrelation nicht akkurat beschreibt.

Unglücklicherweise ist die Berechnung von Integralen mittels STOs computertechnisch schwierig. Frank Boys konnte später jedoch zeigen, dass Linearkombinationen von Gaussian Type Orbitals (GTOs) stattdessen als Näherung dienen können. Da das Produkt zweier GTOs als Linearkombination von GTOs geschrieben werden kann, können Integrale mit einer Gaussian Basisfunktion in geschlossener Form geschrieben werden, was zu einer großen rechnerischen Vereinfachung führt.

In der Literatur sind dutzende Gaussian Type Orbital Basissätze bekannt. Basissätze werden dabei typischerweise in verschiedenen Größen publiziert.Das ermöglicht, systematisch akkuratere Ergebnisse zu erhalten, allerdings sind dann die Kosten höher.

Die kleinsten Basissätze werden als minimale Basissätze bezeichnet. Ein solcher ist ein Basissatz, bei dem für jedes Atom im Molekül eine einzelne Basisfunktion für jedes Orbital einer Hartree-Fock-Rechnung am freien Atom genutzt wird. Da beispielsweise Lithium einen 1s2p-Bindungszustand aufweist, werden für derartige Atome zusätzlich noch p-artige Basisfunktionen zugefügt, die mit den 1s- und 2s-Orbitalen des freien Atoms wechselwirken. Jedes Atom der zweiten Periode des Periodensystems (Lithium bis Neon) würde daher einen Basissatz von fünf Funktionen (zwei s- und drei p-Funktionen) haben.

Eine d-Polarisierungsfunktion wird zu einem p-Orbital addiert

Minimale Basissätze sind für Atome in der Gasphase näherungsweise exakt. Auf der nächsthöheren Ebene werden zusätzliche Funktionen eingeführt, um die Polarisation der Elektronendichte des Atoms im Molekül zu beschreiben. Diese Funktionen werden als Polarisationsfunktionen bezeichnet. Für Wasserstoff umfasst der minimale Basissatz beispielsweise das 1s-Atomorbital, ein einfacher polarisierter Basissatz hat typischerweise zwei s- und eine p-Funktion, die wiederum aus drei Basisfunktionen besteht: p_x, p_y und p_z. Dadurch wird der Basissatz flexibler, da Molekülorbitale, die den Wasserstoff beinhalten, sich asymmetrischer um den Wasserstoffkern verhalten können. Auf ähnliche Weise können zu einem Basissatz mit p-Valenzorbitalen d-artige Funktionen und f-Funktionen zu einem Basissatz mit d-artigen Orbitalen zugefügt werden und so weiter. Dieses Verhalten wird besonders bei der Beschreibung von chemische Bindungen wichtig, da diese oft polarisiert sind.

Weiterhin ist das Hinzufügen von diffusen Funktionen gebräuchlich. Bei diesen handelt es sich um Gaussian-Basisfunktionen mit einem kleinen Exponenten, die die weit vom Kern entfernten Anteile der Atomorbitale flexibler machen. Diffuse Basisfunktionen sind zum Beschreiben von Dipolmomenten wichtig, allerdings spielen sie auch eine entscheidende Rolle für die akkurate Darstellung von intra- und intermolekularen Bindungen.

Minimale Basissätze

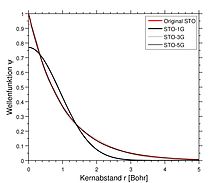
Darstellung verschiedener STO-NG-Orbitale und das zugehörige ursprüngliche STO-Orbital

Die am weitest verbreiteten minimalen Basissätze sind die STO-nG-Basissätze (Slater Type Orbital), wobei n hier ganzzahlig ist. Dieser n-Wert repräsentiert die Anzahl an primitiven Gaußfunktionen (G) aus denen eine einzige Basisfunktion besteht. In dieses Basissätzen umfasst dieselbe Anzahl an primitiven Gaußfunktionen sowohl die Kern- als auch die Valenzorbitale. Minimale Basissätze führen typischerweise zu ungefähren Ergebnissen, die für eine qualitative Publikation ungenügend sind, allerdings sind sie deutlich günstiger als ihre größeren Pendanten. Häufig verwendete minimale Basissätze dieses Typs sind:

STO-3G
STO-4G
STO-6G
STO-3G* - Polarisierte Version von STO-3G

Es werden jedoch auch noch eine Vielzahl an weiteren minimalen Basissätzen wie MidiX genutzt.

Split-valence Basissätze

In den meisten molekularen Bindungen übernehmen die Valenzelektronen den größten Anteil an der Bindung. Aus diesem Grund ist es üblich die Valenzorbitale von mehr als einer Basisfunktion abbilden zu lassen (split-valence), wobei jede von diesen wiederum aus einer festen Linearkombination von primitiven Gaußfunktionen zusammengesetzt sein kann. Basissätze in denen mehrere Basisfunktionen zu einem Valenzorbital gehören werden als Valenz-double-zeta, triple-zeta, quadruple-zeta und so weiter Basissätze bezeichnet. Zeta, ζ, wurde weithin gebraucht um den Exponenten einer STO Basisfunktion darzustellen. Da die unterschiedlichen Orbitale der Aufteilung eine unterschiedliche räumliche Ausdehnung aufweisen, erlaubt es die Kombination der Elektronendichte, die räumliche Ausdehnung so anzupassen, dass sie zu der jeweiligen molekularen Umgebung passt. Im Gegensatz dazu fehlt den minimalen Basissätzen diese Flexibilität.

Pople-Basissätze

Die Nomenklatur dieser split-valence-Basissätze entspringt der Arbeitsgruppe von John Pople und lautet typischerweise X-YZg. Dabei steht X für die Anzahl an primitiven Gaußfunktionen aus denen sich jede Basisfunktion der Kernatomorbitale zusammensetzt. Y und Z geben an, dass sich die Valenzorbitale aus je zwei Basisfunktionen ergeben. Die eine setzt sich wiederum aus einer Linearkombination von Y, die andere aus einer Linearkombination aus Z primitiven Gaußfunktionen. In diesem Fall beinhaltet die Zahl nach dem Bindestrich, dass es sich um einen split-valence double-zeta Basissatz handelt. Split-valence triple- and quadruple-zeta Basissätze werden ebenfalls genutzt und in der Form X-YZWg, X-YZWVg beschrieben. Häufig verwendete split-valence Basissätze dieser Art sind:

3-21G
3-21G* - Polarisationsfunktionen auf Schweratome
3-21G** - Polarisationsfunktionen auf Schweratome und Wasserstoff
3-21+G - Diffuse Funktionen auf Schweratome
3-21++G - Diffuse Funktionen auf Schweratome und Wasserstoff
3-21+G* - Polarisations- und diffuse Funktionen auf Schweratome
3-21+G** - Polarisationsfunktionen auf Schweratome und Wasserstoff und diffuse Funktionen nur auf Schweratome
4-21G
4-31G
6-21G
6-31G
6-31G*
6-31+G*
6-31G(3df, 3pd)
6-311G
6-311G*
6-311+G*

Der 6-31G* Basissatz ist für die Atome Wasserstoff bis Zink definiert und ein polarisierter split-valence double-zeta Basissatz, der im Vergleich zum 6-31G Basissatz noch sechs weitere d-artige kartesische Gaußpolarisationsfunktionen für jedes der Atome Lithium bis Calcium und zehn weitere f-artige kartesische Gaußpolarisationsfunktionen für jedes der Atome Scandium bis Zink aufweist.

Heutzutage gelten die Pople Basissätze als veraltet, da correlation-consistent oder polarization-consistent Basissätze unter Zuhilfenahme ähnlicher Ressourcen typischerweise zu besseren Ergebnissen führen. Außerdem sollte angemerkt werden, dass einige Pople-Basissätze schwerwiegende Defizite aufweisen, die zu falschen Ergebnissen führen können.

Correlation-consistent Basissätze

Einige der am weitest verbreitetsten Basissätze sind diejenigen, die von Thom Dunning und seinen Mitarbeitern entwickelt wurden, da sie dazu designed wurden, Post-Hartree-Fock-Rechnungen systematisch an das Basissatzlimit zu konvergieren und dabei empirische Extrapolationstechniken nutzen.

Für die Atome der ersten und zweiten Periode heißen sie cc-pVNZ, wobei N=D,T,Q,5,6 und so weiter ist, was entsprechend der allgemeinen Nomenklatur für double, triple etc. steht. Das "cc-p" ist die Abkürzung für correlation-consistent polarized (deutsch: korrelations-konsistent polarisiert) und das V zeigt an, dass es sich um valence-only Basissätze handelt. Sie beinhalten aufeinanderfolgende größere Schalen auf Basis von polarisations(abhängigen) Funktionen (d, f, g …). In jüngster Zeit haben sich diese correlation-consistent polarized Basissätze weit verbreitet und gelten als State of the art bei korrelations- oder Post-Hartee-Fock-Rechnungen. Beispiele für diese Klasse an Basissätzen sind folgende:

cc-pVDZ - Double-zeta
cc-pVTZ - Triple-zeta
cc-pVQZ - Quadruple-zeta
cc-pV5Z - Quintuple-zeta
aug-cc-pVDZ, etc. - Erweiterte Versionen der vorhergegangenen Basissätze mit zusätzlichen diffusen Funktionen
cc-pCVDZ - Double-zeta mit Kernkorrelation

Für die Atome der dritten Periode (Aluminium bis Argon), hat es sich herausgestellt, dass zusätzliche Funktionen notwendig sind, weswegen die cc-pV(N+d)Z-Basissätze entwickelt wurden. Noch größere Atome erfordern den Einsatz von pseudopotentialbasierten Basissätzen, cc-pVNZ-PP, oder den relativistisch-kontrahierten Douglas-Kroll-Basissätzen cc-pVNZ-DK. Weitere Modifikationen gibt es unter Einbeziehung der Kernelektronen in Form von core-valence Basissätzen, cc-pCVXZ oder ihren gewichteten Pendants cc-pwCVXZ. Des Weiteren bestehen viele Möglichkeiten zum Zufügen diffuser Funktionen um eine bessere Beschreibung von Anionen und Fernwechselwirkungen (zum Beispiel Van-der-Waals-Kräften) zu ermöglichen.

Bei der Extrapolation von Energiedifferenzen ist Vorsicht geboten, da die einzelnen zur Gesamtenergie beitragenden Komponenten unterschiedlich konvergieren. Die Hartree-Fock-Energie konvergiert exponentiell, die Korrelationsenergie hingegen polynomisch.

Polarization-consistent Basissätze

In der Computerchemie wird mittlerweile sehr viel Dichtefunktionaltheorie genutzt. Allerdings sind die oben beschriebenen correlation-consistent Basissätze hierfür suboptimal, da sie für Post-Hartee-Fock-Rechnungen designet wurden und Dichtefunktionaltheorie eine deutlich schnellere Basissatzkonvergenz aufweist als wellenfunktionbasierte Methoden.

Um eine den correlation-consistent Basissätzen ähnliche Methodologie zu nutzen, stellte die Arbeitsgruppe von Frank Jensen die polarization-consistent (zu Deutsch: polarisationskonsistenten) Basissätze vor. Diese Bilden einen Weg das um Dichtefunktionaltheorierechnungen schnell gegen das gesamte Basissatzlimit konvergieren zu lassen. Analog zu den Dunning-Basissätzen können die pc-n-Basissätze mit Extrapolationstechniken kombiniert werden um CBS-Werte zu erhalten.

Außerdem können die pc-n-Basissätze mit diffusen Funktionen erweitert (englisch: augmented) werden, wodurch aug-pc-n-Basissätze erhalten werden.

Karlsruhe Basissätze

Einige der vielen Valenzanpassungen der Karlsruhe Basissätze sind:

def2-SV(P) - Split valence mit Polarisationsfunktion auf Schweratome (nicht auf Wasserstoff)
def2-SVP - Split valence Polarisierung
def2-SVPD - Split valence Polarisierung mit diffusen Funktionen
def2-TZVP - Triple-zeta Valenzpolarisierung
def2-TZVPD - Triple-zeta Valenzpolarisierung mit diffusen Funktionen
def2-TZVPP - Triple-zeta Valenz mit zwei Sätzen Polarisationsfunktionen
def2-TZVPPD - Triple-zeta Valenz mit zwei Sätzen Polarisations- und einem Satz an diffusen Funktionen
def2-QZVP - Quadruple-zeta Valenzpolarisierung
def2-QZVPD - Quadruple-zeta Valenzpolarisierung mit diffusen Funktionen
def2-QZVPP - Quadruple-zeta mit zwei Sätzen Polarisationsfunktionen
def2-QZVPPD - Quadruple-zeta Valenz mit zwei Sätzen Polarisations- und einem Satz an diffusen Funktionen

Completeness-optimized Basissätze

Gaussian-type Orbitales werden typischerweise darauf optimiert, die niedrigst mögliche Energien für die Systeme zu reproduzieren, die benutzt werden, um den Basissatz zu trainieren. Trotzdem schließt eine Konvergenz der Energie nicht zwangsläufig die Konvergenz von anderen Eigenschaften, wie der magnetischen Abschirmung des Kerns, dem Dipolmoment oder der Dichte des Elektronenimpulses ein, die mit unterschiedlichen Aspekten der elektronischen Wellenfunktion zusammenhängen.

Manninen and Vaara haben daher die completeness-optimized (deutsch: vollständigkeitsoptimierten) Basissätze vorgeschlagen, in denen die Exponenten durch Maximierung des one-electron completeness profiles (deutsch: Einelektronenvollständigkeitsprofil) anstelle der Minimierung der Energie erhalten werden. Complenetess-optimized Basissätze sind eine Möglichkeit das gesamte Basissatzlimit für eine beliebige Eigenschaft auf einer beliebigen Genauigkeit einfach zu erreichen. Außerdem ist die Vorgehensweise einfach zu Automatisieren.

Completeness-optimized Basissätze sind dabei auf eine bestimmte Eigenschaft zugeschnitten. Auf diese Weise kann die Flexibilität des Basissatzes auf die rechnerischen Anforderungen fokussiert werden, was typischerweise zu einer deutlich schnelleren Konvergenz zum vollständigen Basissatzlimit führt, als es mit energieoptimierten Basissätzen möglich ist.

Plane-wave Basissätze

Zusätzlich zu den lokalisierten Basissätzen können auch plane-wave (deutsch: ebene Wellen) Basissätze in quantenchemischen Rechnungen verwendet werden. Typischerweise hängt die Wahl des plane-wave Basissatzes von einer Grenzenergie ab. Die plane-waves in der Simulationsumgebung die zu dem Energiekriterium passen werden dann in der Rechnung verwendet. Diese Basissätze sind besonders populär in Rechnungen, die dreidimensionale periodische Randbedingungen haben.

Der große Vorteil einer plane-wave Basis liegt in der Garantie der Konvergenz zur Zielwellenfunktion in einer geschmeidigen, gleichbleibenden Art und Weise. Im Gegensatz dazu kann eine gleichbleibende Konvergenz zum Basissatzlimit bei lokalisierten Basissätzen aufgrund von Problemen mit der over-completeness (deutsch: Übervollständigkeit) schwierig sein, da in einem großen Basissatz die Funktionen zu verschiedenen Atomen beginnen gleich auszusehen und viele Eigenwerte der Überlappmatrix sich an null annähern.

Zusätzlich sind bei plane-wave Basisfunktionen im Vergleich zu Ihren lokalisierten Gegenstücken bestimmte Integrationen und Vorgänge deutlich einfacher zu programmieren und auszuführen. Beispielsweise ist der Operator der kinetischen Energie im reziproken Raum diagonal. Integrationen über Operatoren des Realraums können mittels schneller Fouriertransformation effizient ausgeführt werden. Die Eigenschaften der Fouriertransformation erlaubt es einen Vektor, der den Gradienten der Gesamtenergie unter Einbeziehung der plane-wave-Koeffizienten repräsentiert unter einem rechnerischen Aufwand, der nach NPW*ln(NPW) skaliert, zu berechnen. NPW ist dabei die Anzahl der plane-waves (englisch: Number of Plane-Waves). Wird diese Eigenschaft mit separierbaren Pseudopotentialen vom Kleinman-Bylander-Typ und vorgefertigten gradientellen, konjugierten Lösungstechniken kombiniert, wird die dynamische Simulation von periodischen Problemen, die hunderte von Atomen betreffen, möglich.

In der Praxis werden plane-wave Basissätze oft in Kombination mit einem effective core potential (deutsch: effektivem Kernpotential) oder Pseudopotential genutzt, sodass die plane-waves nur zur Beschreibung der Valenzladungsdichte genutzt werden. Das hängt damit zusammen, dass sich die Kernelektronen in der Nähe des Atomkerns sehr hoch konzentriert sind, was zu großen Wellenfunktionen und Dichtegradienten in Kernnähe führt, was sich mittels plane-wave Basissätzen nicht einfach beschreiben ist, außer es wird ein sehr hohes Energiekriterium und damit eine kleine Wellenlänge genutzt. Diese kombinierte Methode eines plane-wave-Basissatzes mit einem Kernpseudopotential wird oft als PSPW-Rechnung abgekürzt.

Da alle Funktionen in der Basis weiterhin gemeinsam orthogonal und nicht mit einem bestimmten Atom assoziiert sind, weisen plane-wave Basissätze nicht den Basissatzsuperpositionsfehler auf. Nichtsdestotrotz hängt der plane-wave Basissatz von der Größe der simulierten Umgebung ab, was die Optimierung der Umgebungsgröße verkompliziert.

Aufgrund der Annahme von periodischen Grenzbedingungen sind plane-wave Basissätze für Gasphasenrechnungen weniger geeignet als lokalisierte Basissätze. Um Interaktionen mit dem Molekül und seinen Periodischen Kopien zu vermeiden, müssen daher große Regionen Vakuum an alle Seiten des Gasphasenmoleküls addiert werden. Da die plane-waves eine im Vergleich zu den Regionen, in denen sich das Molekül befindet, ähnliche Genauigkeit nutzen um die Vakuumregionen zu beschreiben, kann es dadurch rechentechnisch kostspielig werden, die wahre Grenze der Nichtinteraktion zu erreichen.

Real-space Basissätze

Analog zu den plane-wave Basissätzen, in denen die Basisfunktion eine Eigenfunktion des Impulsoperators ist, gibt es Basissätze, deren Funktionen Eigenfunktionen des Ortsoperators ist, was Punkte auf einem einheitlichem Netz im realen Raum bedeutet. Reale Implementierungen können allerdings finite Differenzen, finite Elemente oder Lagrange sinc-Funktionen, oder Wavelets nutzen.

Sinc-Funktionen bilden einen orthonormalen, analytischen und vollständigen Basissatz. Die Konvergenz gegen das vollständige Basissatzlimit ist dabei systematisch und relativ einfach. Ähnlich zu plane-wave Basissätzen ist die Genauigkeit von Sinc-Basissätzen durch eine Energiegrenze gegeben.

Im Falle von Wavelets und finiten Elementen ist es möglich das Netz anpassungsfähig zu gestalten, sodass in der Nähe des Kerns mehr Punkte genutzt werden. Wavelets verlassen sich auf den Gebrauch von lokalisierten Funktionen, die die Entwicklung nichtlinearer Skalierungsmethoden ermöglichen.

Siehe auch

Basierend auf einem Artikel in:

Wikipedia.de