
Atomradius
Einem Atom werden zur Vorhersage von Bindungsverhältnissen verschiedenartige Atomradien zugeschrieben. Ein absoluter Radius eines Atoms – und mithin auch eine absolute Größe – kann nicht angegeben werden, da ein Atom nach den Vorstellungen der Quantenmechanik keine definierte Grenze besitzt. Jedoch kann man je nach vorliegendem chemischem Bindungstyp eine effektive Größe des Atoms bestimmen. Sie bezeichnet vereinfacht gesagt den Abstand der Atomkerne in einer gegebenen chemischen Verbindung dieses Typs:
- In überwiegend ionisch aufgebauten Systemen werden den Atomen Ionenradien zugeschrieben.
- Für Atome in molekularen, als kovalent charakterisierten Verbindungen werden Kovalenzradien angegeben.
- In Metallen erhalten die Atome Metallatomradien.
- Zwischen den Molekülen kovalenter Verbindungen wirken Van-der-Waals-Kräfte; entsprechend gibt es dazu die Van-der-Waals-Radien.
Atomradien liegen in der Größenordnung von 10−10 m (=1 Ångström =100 pm =0,1 nm). Der Kovalenzradius im Wasserstoffmolekül beträgt z. B. 32 pm, der Metallradius von 12-fach koordiniertem Cäsium 272 pm.
Zusammenhang mit der Stellung im Periodensystem
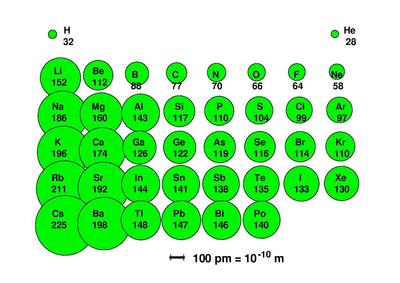
Die Atomradien nehmen innerhalb einer Gruppe des Periodensystems von oben nach unten zu und innerhalb einer Periode von links nach rechts ab. Dies erklärt sich daraus, dass innerhalb einer Periode die Kernladungszahl und damit die positive Ladung des Kerns wächst. Somit werden die negativen Elektronen des Atoms stärker angezogen. Die Verringerung des Atomradius innerhalb der Periode vom Halogen zum Edelgas lässt sich auf die besonders stabile Elektronenkonfiguration der Edelgase zurückführen. Der Anstieg des Radius, von einer Zeile zur nächsten innerhalb jeder Gruppe, resultiert daraus, dass neue Schalen mit Elektronen besetzt werden.
| Ordnungszahl | Symbol | Radius in 10−12 m |
|---|---|---|
| 1 | H | 32 |
| 3 | Li | 152 |
| 4 | Be | 112 |
| 5 | B | 88 |
| 6 | C | 77 |
| 7 | N | 70 |
| 8 | O | 66 |
| 9 | F | 64 |
| 11 | Na | 186 |
| 12 | Mg | 160 |
| 13 | Al | 143 |
| 14 | Si | 117 |
| 15 | P | 110 |
| 16 | S | 104 |
| 17 | Cl | 99 |
| 19 | K | 231 |
| 20 | Ca | 197 |
Metallatomradius, Kugelpackung und Bravais-Gitter
Im einfachsten Fall kristallisiert ein Element so wie in Bild 1 dargestellt (simple cubic, kubisch einfach oder primitiv). Der Durchmesser D eines Atoms (Abstand der Mittelpunkte nächster benachbarter Atome) lässt sich berechnen, indem man von einem Würfel ausgeht, der gerade 1024 Atome enthält und dessen Kanten demnach von 108 Atomen gebildet werden. Ein Mol sind 0,6022∙1024 Atome. Und das sind auch so viel Gramm, wie die Atommasse A angibt. A/0,6022 Gramm ist das Gewicht eines Würfels mit 1024 Atomen. Dividiert man noch durch die Dichte ρ, dann ist A/(0,6022∙ρ) cm3 sein Volumen. Die dritte Wurzel daraus ergibt die Länge einer Kante, und diese durch 108 dividiert ist der Atomdurchmesser D. Beim Element Polonium (A=208,983; ρ=9,196) beträgt das Volumen dieses Würfels 37,737 cm3 und die Kantenlänge 3,354 ;cm. Daraus folgt ein Atomradius von 167,7 ;pm; in Datensammlungen angegeben werden 167,5 pm.

Bei Gold (A=196,967 g/mol; ρ=19,282 g/cm3) stimmt das nicht mehr so genau, der Fehler liegt bei etwa 12%. Der Grund für diese Diskrepanz ist, dass Goldatome nicht kubisch primitiv gepackt sind, sondern dichter (kubisch flächenzentriert, face centered cubic, fcc, eine der beiden dichtesten Kugelpackungen; Bild 2). Dabei sind
- in einer Ebene die Reihen der Atome um einen halben Atomdurchmesser gegeneinander verschoben, so dass sie näher aneinandergerückt werden können, und
- die Atome der Ebene darüber liegen jeweils in einer Mulde zwischen drei anderen Atomen. Sie bilden zusammen Tetraeder.
Charakterisiert man eine Reihe von Atomen durch eine Gerade, die die Atommittelpunkte auffädelt, dann ist der Abstand zweier Reihen in einer Ebene im kubisch-primitiven/sc-Gitter gerade D. Im kubisch-flächenzentrierten/fcc-Gitter ist er kleiner, nämlich D∙(√3/2) (=Höhe eines gleichseitigen Dreiecks) und der Abstand zweier Ebenen ist gleich der Höhe eines Tetraeders [D∙√(2/3)]. Aus dem Produkt der beiden Faktoren findet man: Ein fiktiver Goldwürfel mit kubisch primitiver Kristallstruktur hätte ein um √2≈ 1,41421 größeres Volumen, bzw. seine Dichte wäre um √2 kleiner. Führt man die Rechnung mit der geringeren Dichte durch, erhält man D=288 pm oder r=144 pm, in Übereinstimmung mit dem Ergebnis aus der Röntgenbeugung.
Einfacher geht es, wenn man die Packungsdichten kennt (den Anteil, den die als rund angenommenen Atome am Volumen ausmachen). Ein kubisch primitives Gitter hat eine Packungsdichte von 0,523599, beim kubisch flächenzentrierten beträgt sie 0,740480. Dieselbe Packungsdichte hat auch das hexagonale Gitter (Schichtfolge AB, bei kubisch-flächenzentriert ABC). Der Quotient (0,74../0,52..) ergibt wieder den Faktor √2. In der Tabelle sind Beispiele von Elementen aufgeführt, deren Kristallstruktur kubisch flächenzentriert oder hexagonal ist, zusammen mit dem Ergebnis der Rechnung und dem gemessenen Atomradius.
| Ordnungs zahl |
Element | Kristall struktur |
Atommasse | Dichte | rcalc [pm] | rexp [pm] |
|---|---|---|---|---|---|---|
| 4 | Be | hex | 9,012 | 1,848 | 112,7 | 112 |
| 12 | Mg | hex | 24,305 | 1,738 | 160,1 | 160 |
| 20 | Ca | fcc | 40,078 | 1,55 | 196,5 | 197 |
| 22 | Ti | hex | 47,867 | 4,506 | 146,1 | 147 |
| 27 | Co | hex | 58,933 | 8,86 | 125,0 | 125 |
| 28 | Ni | fcc | 58,693 | 8,908 | 124,6 | 124 |
| 29 | Cu | fcc | 63,546 | 8,933 | 127,8 | 128 |
| 40 | Zr | hex | 91,224 | 6,506 | 160,3 | 160 |
| 46 | Pd | fcc | 106,42 | 12,023 | 137,5 | 137 |
| 47 | Ag | fcc | 107,868 | 10,501 | 144,5 | 144 |
| 57 | La | hex | 138,905 | 6,162 | 187,7 | 187 |
| 76 | Os | hex | 190,23 | 22,59 | 135,2 | 135 |
| 77 | Ir | fcc | 192,217 | 22,56 | 135,7 | 136 |
| 78 | Pt | fcc | 195,084 | 21,45 | 138,7 | 138,5 |
| 79 | Au | fcc | 196,967 | 19,282 | 144,2 | 144 |
Für die kubisch raumzentrierte Elementarzelle (body centered cubic, bcc; Beispiel: Natrium) ist die Packungsdichte 0,68175. Hier muss die Dichte ρ durch (0,68../0,52..) dividiert werden. Das entspricht auch wieder einem um diesen Faktor größeren Volumen eines fiktiven Würfels mit sc-Struktur. Bei Natrium (A=22,9898; ρ=0,968) erhält man aus der dritten Wurzel aus [22,9898/(0,6022∙0,968)]∙(0,68../0,52..) ein D=371,4 pm und r =185,7 pm; gemessen wurden 186 pm.
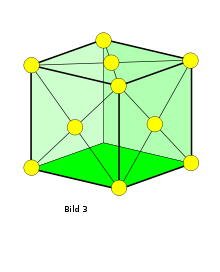
Die klassische kristallographische Methode zählt, wie viele Atome eine Elementarzelle umfasst. Diese enthält, im Fall kubisch-flächenzentriert (fcc), Anteile von vier ganzen Atomen (Bild 3). Aus der Atommasse, der Dichte und der Avogadro-Zahl lässt sich das Volumen ermitteln, in dem sich vier Atome befinden, also die Größe der Elementarzelle (in diesem Fall von der Form eines Würfels). Der Durchmesser eines Atoms ist der Abstand der Mittelpunkte zweier Atome, die den kleinsten in der Zelle vorkommenden Abstand aufweisen. Sie sind entlang der Flächendiagonalen angeordnet (und nicht entlang der Kante, da sind sie weiter voneinander entfernt). Diese ist vier Atomradien lang (in Bild 3 sind die Atome der Übersichtlichkeit wegen kleiner eingezeichnet). Aus dem Volumen erhält man die Kantenlänge, die Länge der Diagonale und so den Atomradius. Mit der kubisch-primitiven Elementarzelle lässt sich die Rechnung auch für Polonium durchführen.
Siehe auch
- Bindungslängen in kovalenten Systemen
- Lanthanoidenkontraktion


© biancahoegel.de;
Datum der letzten Änderung: Jena, den: 02.10. 2021