Lebesguesche Überdeckungsdimension

Die Lebesgue’sche Überdeckungsdimension (nach Henri Léon Lebesgue) ist eine geometrisch sehr anschauliche, topologische Charakterisierung der Dimension.

Definition

Ein topologischer Raum hat die Dimension , wenn die kleinste natürliche Zahl ist, derart dass es zu jeder offenen Überdeckung $(U_{i})_{i}$ eine feinere offene Überdeckung $(V_{j})_{j}$ gibt, so dass jeder Punkt aus in höchstens n+1 der Mengen $V_{j}$ liegt. Gibt es kein solches , so heißt von unendlicher Dimension.

Die Dimension von wird mit $\dim(X)$ bezeichnet. Da es eine ganze Reihe weiterer Dimensionsbegriffe gibt, spricht man genauer von der Lebesgue’schen Überdeckungsdimension.

Erläuterung

Dabei ist $(U_{i})_{i}$ eine offene Überdeckung von , wenn jedes $U_{i}$ offen und die Vereinigung der $U_{i}$ ist. Die Überdeckung $(V_{j})_{j}$ heißt feiner als $(U_{i})_{i}$ , wenn jedes $V_{j}$ in irgendeinem $U_{i}$ enthalten ist.

Anschaulich stellt die Überdeckung $(U_{i})_{i}$ in obiger Definition eine Größenbeschränkung für Überdeckungsmengen dar. In diesem Sinne gibt es also zu beliebiger Größenbeschränkung stets Überdeckungen, bei denen sich höchstens jeweils n+1 Mengen überschneiden. In der Tat lässt sich die Überdeckungsdimension bei kompakten metrischen Räumen wie folgt umformulieren. Ein kompakter metrischer Raum hat die Dimension , wenn die kleinste natürliche Zahl ist, derart dass es zu jedem $\varepsilon >0$ eine offene Überdeckung $(V_{j})_{j}$ gibt, so dass $\operatorname {diam}(V_{j})<\varepsilon$ für alle und jeder Punkt aus in höchstens n+1 der Mengen $V_{j}$ liegt. Dabei bezeichnet $\operatorname {diam}(V_{j})$ den Durchmesser von $V_{j}$ .

Obige Definition ist rein topologisch, das heißt, es ist nur von offenen Mengen die Rede. Daher ist die Lebesgue’sche Überdeckungsdimension eine topologische Invariante, homöomorphe Räume haben also dieselbe Dimension.

Beispiele

Beispiel für die Lebesgue’sche Überdeckungsdimension

Einfache Beispiele

Jeder endliche Hausdorff-Raum ist 0-dimensional, denn jeder Punkt liegt in einer minimalen offenen Menge. Sind $V_{1},\dotsc ,V_{k}$ die minimalen offenen Mengen, so ist $(V_{j})_{j}$ feiner als jede Überdeckung und jeder Punkt liegt in genau einem $V_{j}$ .

Jeder diskrete Raum (z.B. die Menge der ganzen Zahlen) ist 0-dimensional, denn jeder Punkt liegt in einer minimalen offenen Menge.

Das Cantor’sche Diskontinuum ist ein 0-dimensionaler kompakter Hausdorffraum mit überabzählbar vielen Punkten.

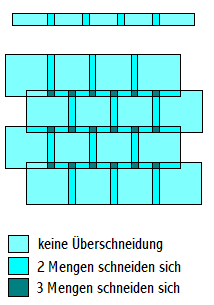
Eine Strecke, etwa das Einheitsintervall , ist eindimensional. Wie der obere Teil nebenstehender Zeichnung plausibel macht, kann man stets beliebig feine offene Überdeckungen finden, bei denen sich höchstens je zwei Mengen schneiden. Daher ist die Dimension $\le 1$ . Diese Überschneidungen sind unvermeidbar; leicht überlegt man sich, dass sonst nicht zusammenhängend sein könnte. Daher ist die Dimension sogar .

Die nebenstehende Zeichnung zeigt auch, dass es zu ebenen Figuren wie Kreisflächen oder Rechtecken usw. stets beliebig feine Überdeckungen gibt, bei denen jeder Punkt in höchstens 3 Mengen enthalten ist. Die Dimension ist also $\leq 2$ . Leicht verallgemeinert man das auf höhere Dimensionen, so hat etwa eine Kugel im ${\mathbb R}^n$ die Dimension $\leq n$ . Dass hier in der Tat Gleichheit vorliegt, ist ein schwierigerer Satz, zu dessen Beweis kombinatorische Argumente herangezogen werden.

Der Hilbertwürfel ist ein Beispiel für einen unendlichdimensionalen, kompakten, metrischen Raum.

Satz (Kugeln, Quader, Simplizes)

Kugeln, nicht-entartete Quader oder nicht-entartete Simplizes im ${\mathbb R}^n$ haben die Lebesgue’sche Überdeckungsdimension .

Dieser Satz ist historisch bedeutsam: Es war lange nicht klar, ob man die Einheitswürfel im ${\mathbb R}^n$ und ${\mathbb R}^m$ , die jeweils mit der Produkttopologie versehen sind, für $n\not =m$ topologisch unterscheiden kann, also ob man sie als nicht-homöomorph nachweisen kann. Es hatte die Mathematiker überrascht, als Georg Cantor bijektive Abbildungen zwischen unterschiedlichdimensionalen Räumen angegeben hatte, die allerdings unstetig waren. Giuseppe Peano hatte stetige und surjektive Abbildungen von [0,1] nach $[0,1]^{2}$ konstruiert, diese waren nicht bijektiv, siehe Peano-Kurve. Es war also nicht auszuschließen, dass eine geschickte Kombination dieser Konstruktionen zu einem Homöomorphismus zwischen Würfeln unterschiedlicher Dimension führen könnte. Dass dies tatsächlich nicht möglich ist, zeigt obiger Satz, der erstmals von Luitzen Egbertus Jan Brouwer bewiesen wurde.

Einbettungssatz von Menger-Nöbeling

Es stellt sich die Frage, ob sich endlichdimensionale topologische Räume homöomorph in einen ${\mathbb R}^n$ einbetten lassen, d.h. ob sie homöomorph zu einer Teilmenge des ${\mathbb R}^n$ sind. Wie die Kreislinie zeigt, kann zur Einbettung eines eindimensionalen Raumes die Ebene ${{\mathbb R}}^{2}$ erforderlich sein. Die Frage nach einer oberen Grenze für diese Dimension beantwortet folgender Satz von Menger-Nöbeling.

Ein -dimensionaler kompakter metrischer Raum gestattet homöomorphe Einbettungen in den ${{\mathbb R}}^{{2n+1}}$ .

Vererbung der Dimension

Ist ein kompakter, metrischer Raum und $Y\subset X$ ein Unterraum, so ist $\dim(Y)\leq \dim(X)$ .

Bei Quotientenräumen, d.h. bei surjektiven stetigen Abbildungen, ergibt sich ein überraschendes Verhalten: Jeder kompakte metrische Raum ist stetiges Bild des 0-dimensionalen Cantor’schen Diskontinuums.

Sind und metrisierbar, so gilt $\dim(X\times Y)\leq \dim(X)+\dim(Y)$ . Gleichheit gilt im Allgemeinen nicht, ein Gegenbeispiel ist $X=Y=l^{2}({\mathbb Q})$ .

Es gilt die folgende als Hurewicz-Formel bekannte Abschätzung: Ist normal, metrisierbar und $f\colon X\to Y$ eine stetige, abgeschlossene und surjektive Abbildung, so gilt

$\mathrm {dim} (X)\leq \mathrm {dim} (Y)+\sup _{y\in Y}\mathrm {dim} (f^{-1}(y))$ .

Beachte, dass daraus leicht obige Abschätzung für die Dimension des kartesischen Produktes metrischer Räume folgt.

Vergleich mit anderen Dimensionsbegriffen

Ist ein normaler Raum, so ist die Lebesgue’sche Dimension stets kleiner oder gleich der großen induktiven Dimension. Für metrisierbare Räume gilt Gleichheit.

Siehe auch

Asymptotische Dimension

Literatur

Wolfgang Franz: Topologie. Band 1: Allgemeine Topologie (Sammlung Göschen. 1181, ZDB-ID 842269-2). de Gruyter, Berlin 1960.

Basierend auf einem Artikel in:

Wikipedia.de