Gauß-Prozess
Ein Gaußprozess (nach Carl Friedrich Gauß) ist in der Wahrscheinlichkeitstheorie ein stochastischer Prozess, bei dem jede endliche Teilmenge von Zufallsvariablen mehrdimensional normalverteilt (gaußverteilt) ist. Verallgemeinert stellt ein Gaußprozess zeitliche, räumliche oder beliebige andere Funktionen dar, deren Funktionswerte aufgrund unvollständiger Information nur mit bestimmten Unsicherheiten und Wahrscheinlichkeiten modelliert werden können. Konstruiert wird er aus Funktionen der Erwartungswerte, Varianzen und Kovarianzen und beschreibt damit die Funktionswerte als ein Kontinuum aus korrelierten Zufallsvariablen in Form einer unendlichdimensionalen Normalverteilung. Ein Gaußprozess ist somit eine Wahrscheinlichkeitsverteilung von Funktionen. Eine Stichprobe daraus ergibt eine zufällige Funktion mit bestimmten bevorzugten Eigenschaften.
Anwendungen
Angewendet werden Gaußprozesse zur mathematischen Modellierung des Verhaltens von nicht-deterministischen Systemen auf der Basis von Beobachtungen. Gaußprozesse eignen sich zur Signalanalyse und -synthese, bilden ein mächtiges Werkzeug bei der Interpolation, Extrapolation oder Glättung beliebig-dimensionaler diskreter Messpunkte (Gaußprozess-Regression bzw. Kriging-Verfahren) und finden Anwendung in Klassifizierungsproblemen. Gaußprozesse können wie ein überwachtes Maschinenlernverfahren zur abstrakten Modellierung anhand von Trainingsbeispielen verwendet werden, wobei kein iteratives Training wie bei neuronalen Netzen notwendig ist. Stattdessen werden Gaußprozesse sehr effizient mit linearer Algebra aus statistischen Größen der Beispiele abgeleitet und sind dabei mathematisch klar interpretierbar und gut kontrollierbar. Außerdem wird für jeden einzelnen Ausgabewert ein zugehöriges Vertrauensintervall berechnet, das den eigenen Vorhersagefehler präzise schätzt, während bekannte Fehler der Eingabewerte korrekt fortgepflanzt werden.
Mathematische Beschreibung
Definition
Ein Gaußprozess ist ein spezieller stochastischer
Prozess
auf einer beliebigen Indexmenge
,
wenn seine endlichdimensionalen Verteilungen mehrdimensionale
Normalverteilungen (auch Gauß-Verteilungen) sind. Es soll also für alle
die multivariate
Verteilung von
durch eine
-dimensionale
Normalverteilung gegeben sein.
Begriff: Obwohl historisch bedingt das Wort Prozess mit einem zeitlichen Vorgang assoziiert wird, ist ein stochastischer Prozess oder Gaußprozess nur die mathematische Beschreibung einer Unbestimmtheit von beliebigen kontinuierlichen Funktionen. Ein Gaußprozess ist wie eine Wahrscheinlichkeitsverteilung zu verstehen. Eine treffendere Bezeichnung wäre beispielsweise Gaußkontinuum.
Notation
Analog zur ein- und mehrdimensionalen Gaußverteilung ist ein Gaußprozess über
seine ersten beiden Momente
vollständig und eindeutig bestimmt. Bei der mehrdimensionalen Gaußverteilung
sind dies der Erwartungswertvektor
und die Kovarianzmatrix
.
Beim Gaußprozess treten an deren Stelle eine Erwartungswertfunktion
und eine Kovarianzfunktion
.
Diese Funktionen können im einfachsten Fall als Vektor mit kontinuierlichen
Zeilen bzw. als Matrix mit kontinuierlichen Zeilen und Spalten aufgefasst
werden. Folgende Tabelle vergleicht eindimensionale und mehrdimensionale
Gaußverteilungen mit Gaußprozessen. Das Symbol
kann gelesen werden als "ist verteilt wie".
| Art der Verteilung | Notation | Größen | Wahrscheinlichkeitsdichtefunktion |
|---|---|---|---|
| Eindimensionale Gaußverteilung | |||
| Mehrdimensionale Gaußverteilung | |||
| Gaußprozess | (keine analytische Darstellung) |
Die Wahrscheinlichkeitsdichtefunktion eines Gaußprozesses lässt sich nicht
analytisch darstellen, da es keine entsprechende Notation für Operationen mit
kontinuierlichen Matrizen gibt. Das erweckt den Eindruck, dass man mit
Gaußprozessen nicht wie mit endlichdimensionalen Normalverteilungen rechnen
kann. Tatsächlich ist aber die wesentliche Eigenschaft des Gaußprozesses nicht
die Unendlichkeit der Dimensionen, sondern vielmehr die Zuordnung der
Dimensionen zu bestimmten Koordinaten einer Funktion. In praktischen Anwendungen
hat man es immer nur mit endlich vielen Stützstellen zu tun und kann daher alle
Berechnungen wie im endlichdimensionalen Fall durchführen. Der Grenzwert für
unendlich viele Dimensionen wird dabei nur in einem Zwischenschritt benötigt,
nämlich dann, wenn Werte an neuen interpolierten Stützstellen ausgelesen werden
sollen. In diesem Zwischenschritt wird der Gaußprozess, d.h. die
Erwartungswertfunktion und Kovarianzfunktion, durch geeignete analytische
Ausdrücke dargestellt bzw. approximiert. Dabei erfolgt die Zuordnung zu den
Stützstellen direkt über die parametrisierten Koordinaten
im analytischen Ausdruck. Im endlichdimensionalen Fall mit diskreten
Stützstellen werden die notierten Koordinaten
den Dimensionen über ihre Indizes zugeordnet.
Beispiel eines Gaußprozesses
Als ein einfaches Beispiel sei ein Gaußprozess
mit einer skalaren Variable
(Zeit) durch die Erwartungswertfunktion
und Kovarianzfunktion
gegeben. Dieser Gaußprozess beschreibt ein endloses zeitliches elektrisches Signal mit gaußschem weißen Rauschen mit einer Standardabweichung von einem Volt um eine mittlere Spannung von 5 Volt.
Definitionen spezieller Eigenschaften
Ein Gaußprozess heißt zentriert, wenn sein Erwartungswert konstant
0 ist, also wenn
für alle
.
Ein Gaußprozess heißt stationär, wenn seine Kovarianzfunktion
translationsinvariant ist, also durch eine relative Funktion
beschrieben werden kann.
Ein Gaußprozess mit isotropen
Eigenschaften heißt radial, wenn seine Kovarianzfunktion durch eine
radialsymmetrische und auch stationäre Funktion
mit einem eindimensionalen Parameter mit der Euklidischen
Norm
beschrieben werden kann.
Liste gängiger Gaußprozesse und Kovarianzfunktionen
- Konstant:
und
- Entspricht einem konstanten Wert aus einer Gaußverteilung mit
Standardabweichung
.
- Offset:
und
- Entspricht einem konstanten Wert, der durch
fest vorgegeben ist.
- Gaußsches Weißes
Rauschen:
- (
: Standardabweichung,
: Kronecker-Delta)
- Rational quadratisch:
- Gamma-Exponentiell:
- Ornstein-Uhlenbeck
/ Gauß-Markov:
- Beschreibt stetige, nicht-differenzierbare Funktionen, außerdem weißes Rauschen, nachdem es einen RC-Tiefpass-Filter durchlaufen hat.
- Quadratisch exponentiell:
- Beschreibt glatte unendlich oft differenzierbare Funktionen.
- Matérn:
- Sehr universell verwendbare Gaußprozesse zur Beschreibung der meisten
typischen Messkurven. Die Funktionen des Gaußprozesses sind
-mal stetig differenzierbar, wenn
. Gängige Spezialfälle sind:
entspricht der Ornstein-Uhlenbeck-Kovarianzfunktion und
der quadratisch exponentiellen.
- Periodisch:
- Funktionen von diesem Gaußprozess sind sowohl periodisch mit der
Periodendauer
als auch glatt (quadratisch exponentiell).
- Polynomial:
- Wächst nach außen stark an und ist meist eine schlechte Wahl bei Regressionsproblemen, kann aber bei hochdimensionalen Klassifizierungsproblemen nützlich sein. Sie ist positiv semidefinit und erzeugt nicht notwendigerweise invertierbare Kovarianzmatrizen.
- Brownsche
Brücke:
und
- Wiener-Prozess:
und
- Entspricht der Brownschen Bewegung
- Ito-Prozess:
Ist
und
,
zwei integrierbare reellwertige Funktionen sowie
ein Wiener-Prozess, so ist der Ito-Prozess
- ein Gaußprozess mit
und
.
Bemerkungen:
ist die Distanz bei stationären und radialen Kovarianzfunktionen
ist die charakteristische Längenskala der Kovarianzfunktion bei der die Korrelation auf etwa
abgefallen ist.
- Die meisten stationären Kovarianzfunktionen
werden auf
normiert notiert und sind somit gleichbedeutend zu Korrelationsfunktionen. Für den Gebrauch als Kovarianzfunktion werden sie mit einer Varianz
multipliziert, was den Variablen eine Skalierung und/oder physikalische Einheit zuordnet.
- Kovarianzfunktionen dürfen nicht beliebige Funktionen
oder
sein, da sichergestellt sein muss, dass sie positiv definit sind. Positiv semidefinite Funktionen sind ebenfalls gültige Kovarianzfunktionen, wobei zu beachten ist, dass diese nicht notwendigerweise invertierbare Kovarianzmatrizen ergeben und daher meistens mit einer positiv definiten Funktion kombiniert werden.
Rechenoperationen mit Gaußprozessen
Mit Gaußprozessen können verschiedene stochastische Rechenoperationen
durchgeführt werden mit denen unterschiedliche Signale oder Funktionen
miteinander in Verbindung gebracht oder aus einander extrahiert werden können.
Die Operationen werden im Folgenden in der Vektor- und Matrixschreibweise für
endlich viele Stützstellen
dargestellt, was analog auf Erwartungswertfunktionen
und Kovarianzfunktionen
übertragbar ist.
Lineare Transformation
Addition: unkorrelierte Signale
Wird die Summe von zwei unabhängigen unkorrelierten Signalen gebildet, dann addieren sich deren Erwartungswertfunktionen und deren Kovarianzfunktionen:
Die zugehörigen Wahrscheinlichkeitsdichtefunktionen erfahren dadurch eine Faltung.
Addition: korrelierte Signale
Bei zwei vollständig korrelierten Signalen lässt sich die Summe durch eine
skalare Multiplikation
ausdrücken. Sind beide Signale identisch, ergibt sich .
Differenz: unkorrelierte Signale
Wird die Differenz von zwei unabhängigen unkorrelierten Signalen gebildet, dann subtrahieren sich deren Erwartungswertfunktionen und es addieren sich deren Kovarianzfunktionen:
Subtraktion eines korrelierten Anteils
Wenn das Signal y2 eines Gaußprozesses einen korrelierten additiven Anteil des Signals y1 eines anderen Gaußprozesses beschreibt, dann bewirkt die Subtraktion dieses Anteils die Subtraktion der Erwartungswertfunktion und der Kovarianzfunktion:
Der Rückstrich-Operator
wurde hier symbolisch verwendet im Sinne von "ohne den enthaltenen
Anteil".
Multiplikation
Die Multiplikation mit einer beliebigen Matrix
enthält auch die Spezialfälle des Produkts mit einer Funktion (Diagonalmatrix
)
oder mit einem Skalar (
):
Hier sei darauf hingewiesen, dass ein Produkt der Funktionen zweier Gaußprozesse miteinander keinen weiteren Gaußprozess ergäbe, da die resultierende Wahrscheinlichkeitsverteilung die Eigenschaft der Gaußförmigkeit verloren hätte.
Allgemeine lineare Transformation
Alle bisher gezeigten Operationen sind Spezialfälle der allgemeinen linearen Transformation:
Dieser Zusammenhang[1]
beschreibt die Summe
mit den konstanten Matrizen
und
und den Signalen
und
zweier Gaußprozesse. Die Kreuzkovarianzmatrix
beschreibt eine gegebene Korrelation zwischen
und
.
Das kombinierte Signal ist zu den beiden ursprünglichen Signalen korreliert mit
den Kreuzkovarianzmatrizen
zu
und
zu
.[2]
Eine Kreuzkovarianzmatrix
zwischen zwei Signalen
und
kann mit deren Kovarianzmatrizen
und
in eine Kreuzkorrelationsmatrix
umgerechnet werden über den Zusammenhang
.
Fusion
Wenn dieselbe unbekannte Funktion durch zwei verschiedene und unabhängige Gaußprozesse beschrieben wird, dann kann durch diese Operation die Vereinigung oder Fusion der beiden unvollständigen Informationen gebildet werden:
Das Resultat entspricht dem Überlapp bzw. dem auf Eins renormierten Produkt der beiden Wahrscheinlichkeitsdichtefunktionen und beschreibt den wahrscheinlichsten Gaußprozess unter Berücksichtigung beider Teilinformationen. Die Ausdrücke können bei Bedarf so erweitert werden, dass in jedem möglichen Fall nur eine Matrixinversion durchgeführt werden muss:
Zerlegung
Ein gegebenes Signal
kann in seine additiven Komponenten zerlegt werden, wenn die
A-Priori-Gaußprozesse der Bestandteile und des gesamten Signals gegeben sind.
Gemäß der Additionsregel
setzt sich der Gaußprozess des gesamten Signals
aus den A-Priori-Gaußprozessen der Anteile zusammen. Die einzelnen
Komponenten
können dann durch die A-posteriori-Gaußprozesse
- und Kreuzkovarianzen zwischen den Signalen
geschätzt werden. Die resultierenden einzelnen Komponenten des Signals können mehrdeutig sein und sind daher gekoppelte Wahrscheinlichkeitsverteilungen möglicher Lösungen um die jeweils wahrscheinlichste Lösung (siehe Beispiel: Signalzerlegung).
Gaußprozess-Regression
Einleitung
Gaußprozesse können zur Interpolation, Extrapolation oder Glättung von
diskreten Messdaten einer Abbildung
verwendet werden. Diese Anwendung von Gaußprozessen nennt man
Gaußprozess-Regression. Oft wird die Methode aus historischen Gründen besonders
in der räumlichen Domäne als Kriging-Verfahren bezeichnet. Sie eignet
sich insbesondere für Probleme, für die keine spezielle Modellfunktion bekannt
ist. Ihre Eigenschaft als Maschinenlernverfahren ermöglicht eine automatische
Modellbildung auf der Basis von Beobachtungen. Dabei erfasst ein Gaußprozess das
typische Verhalten des Systems, womit die für das Problem optimale Interpolation
abgeleitet werden kann. Als Ergebnis erhält man eine
Wahrscheinlichkeitsverteilung von möglichen Interpolationsfunktionen sowie die
Lösung mit der höchsten Wahrscheinlichkeit.
Überblick über die einzelnen Schritte
Die Berechnung einer Gaußprozess-Regression kann durch folgende Schritte durchgeführt werden:
- A-priori-Erwartungswertfunktion: Liegt ein gleichbleibender Trend in den Messwerten vor, wird eine A-priori-Erwartungswertfunktion zum Ausgleich des Trends gebildet.
- A-priori-Kovarianzfunktion: Die Kovarianzfunktion wird nach bestimmten qualitativen Eigenschaften des Systems ausgewählt oder aus Kovarianzfunktionen unterschiedlicher Eigenschaften nach bestimmten Regeln zusammengesetzt.
- Feinabstimmung der Parameter: um quantitativ korrekte Kovarianzen zu erhalten, wird die gewählte Kovarianzfunktion auf die vorhandenen Messwerte gezielt oder durch ein Optimierungsverfahren angepasst bis die Kovarianzfunktion die empirischen Kovarianzen wiedergibt.
- Bedingte Verteilung: Durch Berücksichtigung von bekannten Messwerten wird aus dem A-priori-Gaußprozess der bedingte A-posteriori-Gaußprozess für neue Stützstellen mit noch unbekannten Werten berechnet.
- Interpretation: Aus dem A-posteriori-Gaußprozess wird schließlich die Erwartungswertfunktion als die bestmögliche Interpolation abgelesen und gegebenenfalls die Diagonale der Kovarianzfunktion als die ortsabhängige Varianz.
Schritt 1: A-priori-Erwartungswertfunktion
Ein Gaußprozess ist durch eine Erwartungswertfunktion und eine Kovarianzfunktion vollständig definiert. Die Erwartungswertfunktion ist die A-priori-Schätzung des Regressionsproblems und beschreibt einen im Voraus bekannten Offset oder Trend der Daten. Die Funktion lässt sich oft durch ein einfaches Polynom beschreiben, das zur Kovarianzfunktion passend geschätzt werden kann, und in sehr vielen Fällen auch durch einen konstanten Mittelwert. Bei asymmetrischen nicht-gaußförmigen Verteilungen mit nur positiven Werten kann mitunter auch ein Mittelwert von Null die besten Ergebnissen liefern.
Schritt 2: A-priori-Kovarianzfunktion
In praktischen Anwendungen muss aus endlich vielen diskreten Messwerten oder
endlich vielen Beispielkurven ein Gaußprozess bestimmt werden. In Analogie zur
eindimensionalen Gaußverteilung, die über den Mittelwert und die
Standardabweichung diskreter Messwerte vollständig bestimmt ist, würde man zur
Berechnung eines Gaußprozesses mehrere einzelne, jedoch vollständige Funktionen
erwarten, um damit die Erwartungswertfunktion
und die (empirische) Kovarianzfunktion
zu berechnen.
Regressionsproblem und stationäre Kovarianz
Meist liegt jedoch keine solche Verteilung exemplarischer Funktionen vor.
Beim Regressionsproblem sind stattdessen nur diskrete Stützstellen einer
einzelnen Funktion bekannt, die interpoliert oder geglättet werden soll. Auch in
einem solchen Fall kann ein Gaußprozess ermittelt werden. Dazu wird anstatt
dieser einen Funktion eine Schar aus vielen zueinander verschobenen Kopien der
Funktion betrachtet. Diese Verteilung lässt sich nun mithilfe einer
Kovarianzfunktion beschreiben. Meist kann sie als relative Funktion dieser
Verschiebung durch
ausgedrückt werden. Sie heißt dann stationäre Kovarianzfunktion und gilt
gleichermaßen für alle Orte der Funktion und beschreibt die immer gleiche (also
stationäre) Korrelation eines Punkts zu seiner Nachbarschaft, sowie die
Korrelation benachbarter Punkte untereinander.
Die Kovarianzfunktion wird analytisch dargestellt und heuristisch bestimmt oder in der Literatur nachgeschlagen. Die freien Parameter der analytischen Kovarianzfunktionen werden an die Messwerte angepasst. Sehr viele physikalische Systeme weisen eine ähnliche Form der stationären Kovarianzfunktion auf, so dass mit wenigen tabellierten analytischen Kovarianzfunktionen die meisten Anwendungen beschrieben werden können. So gibt es beispielsweise Kovarianzfunktionen für abstrakte Eigenschaften wie Glattheit, Rauigkeit (fehlende Differenzierbarkeit), Periodizität oder Rauschen, die nach bestimmten Vorschriften kombiniert und angepasst werden können, um die Eigenschaften der Messwerte nachzubilden.
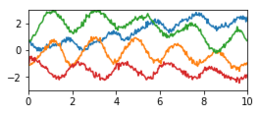
Beispiele stationärer Kovarianz
Die folgende Tabelle zeigt Beispiele von Kovarianzfunktionen mit solchen
abstrakten Eigenschaften. Die Beispiel-Kurven sind zufällige Stichproben des
jeweiligen Gaußprozesses und repräsentieren typische Kurvenverläufe. Sie wurden
mit der jeweiligen Kovarianzmatrix
und einem Zufallsgenerator
für mehrdimensionale Normalverteilungen als korrelierter Zufallsvektor
erzeugt. Die stationären Kovarianzfunktionen
werden hier als eindimensionale Funktionen
mit
abgekürzt.
| Eigenschaft | Beispiele stationärer Kovarianzfunktionen | Zufallsfunktionen |
|---|---|---|
| Konstant | 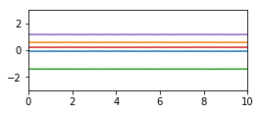 | |
| Glatt |  | |
| Rau | 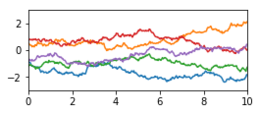 | |
| Periodisch | 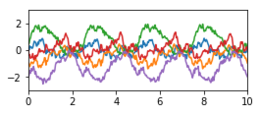 | |
| Rauschen | 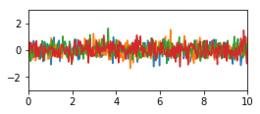 | |
| Gemischt (periodisch, glatt und verrauscht) |
 |
Konstruktion neuer Kovarianzfunktionen
Die Eigenschaften können nach bestimmten Rechenvorschriften kombiniert werden. Das grundsätzliche Ziel bei der Konstruktion einer Kovarianzfunktion ist, die wahren Kovarianzen möglichst gut wiederzugeben, während gleichzeitig die Bedingung der positiven Definitheit erfüllt wird. Die gezeigten Beispiele, außer die Konstante, besitzen letztere Eigenschaft und auch die Additionen und Multiplikationen solcher Funktionen bleiben positiv definit. Die konstante Kovarianzfunktion ist nur positiv semidefinit und muss mit mindestens einer positiv definiten Funktion kombiniert werden. Die unterste Kovarianzfunktion in der Tabelle zeigt eine mögliche Mischung verschiedener Eigenschaften. Die Funktionen in diesem Beispiel sind über eine bestimmte Distanz hinweg periodisch, weisen ein relativ glattes Verhalten auf und sind mit einem bestimmten Messrauschen überlagert.
Bei gemischten Eigenschaften gilt:
- Bei additiven Effekten, wie dem übergelagerten Messrauschen, werden die Kovarianzen addiert.
- Bei sich gegenseitig verstärkenden oder abschwächenden Effekten, wie dem langsamen Abklingen der Periodizität, werden die Kovarianzen multipliziert.
Mehrdimensionale Funktionen
Was hier mit eindimensionalen Funktionen gezeigt ist, lässt sich analog auch
auf mehrdimensionale Systeme übertragen, indem lediglich der Abstand
durch eine entsprechende n-dimensionale Abstandsnorm ersetzt wird. Die
Stützpunkte in den höheren Dimensionen werden in einer beliebigen Reihenfolge
abgewickelt und mit Vektoren dargestellt, so dass sie genauso wie im
eindimensionalen Fall verarbeitet werden können. Die beiden folgenden
Abbildungen zeigen zwei Beispiele mit zweidimensionalen Gaußprozessen und
unterschiedlichen stationären und radialen Kovarianzfunktionen. In der rechten
Abbildung ist jeweils eine zufällige Stichprobe des Gaußprozesses dargestellt.
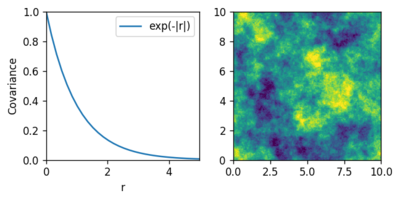
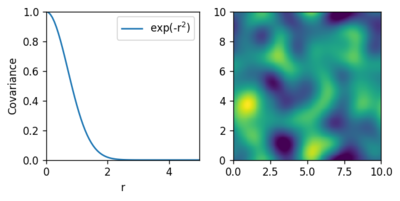
Nicht-stationäre Kovarianzfunktionen
Gaußprozesse können auch nicht-stationäre Eigenschaften der Kovarianzfunktion besitzen, also relative Kovarianzfunktionen, die sich als Funktion des Ortes ändern. In der Literatur wird beschrieben, wie nicht-stationäre Kovarianzfunktionen konstruiert werden können, so dass auch hier die positive Definitheit sichergestellt wird. Eine einfach Möglichkeit ist z.B. eine Interpolation unterschiedlicher Kovarianzfunktionen über den Ort mit der inversen Distanzwichtung.
Schritt 3: Feinabstimmung der Parameter
Die qualitativ konstruierten Kovarianzfunktionen enthalten Parameter, sogenannte Hyperparameter, die an das System angepasst werden müssen, um quantitativ korrekte Ergebnisse erzielen zu können. Dies kann durch direktes Wissen über das System erfolgen, z.B. über den bekannten Wert der Standardabweichung des Messrauschens oder die A-priori-Standardabweichung des Gesamtsystems (sigma prior, entspricht quadriert den Diagonalelementen der Kovarianzmatrix).
Die Parameter können aber auch automatisch angepasst werden. Dazu verwendet man die Randwahrscheinlichkeit, also die Wahrscheinlichkeitsdichte für eine gegebene Messkurve als ein Maß für die Übereinstimmung zwischen dem vermuteten Gaußprozess und einer vorhandenen Messkurve. Die Parameter werden dann so optimiert, dass diese Übereinstimmung maximal wird. Da die Exponentialfunktion streng monoton ist, genügt es, den Exponenten der Wahrscheinlichkeitsdichtefunktion zu maximieren, die sogenannte Log-Marginal-Likelihood-Funktion
mit dem Messwert-Vektor
der Länge
und der von Hyperparametern abhängigen Kovarianzmatrix
.
Mathematisch bewirkt die Maximierung der Randwahrscheinlickeit eine optimale
Abwägung zwischen der Genauigkeit (Minimierung der Residuen) und der Einfachheit
der Theorie. Ein einfache Theorie zeichnet sich durch große
Nebendiagonalelemente aus, wodurch eine hohe Korrelation im System beschrieben
wird. Das bedeutet, dass wenige Freiheitsgrade im System vorhanden sind und
somit die Theorie in gewisser Weise mit wenigen Regeln auskommt, um alle
Zusammenhänge zu erklären. Sind diese Regeln zu einfach gewählt, würden die
Messungen nicht hinreichend gut wiedergegeben werden und die residuellen Fehler
wachsen zu stark an. Bei einer maximalen Randwahrscheinlichkeit ist das
Gleichgewicht einer optimalen Theorie gefunden, sofern hinreichend viele
Messdaten für eine gute Konditionierung zur Verfügung standen. Diese implizite
Eigenschaft der Maximum-Likelihood-Methode
kann auch als Ockhams
Sparsamkeitsprinzip verstanden werden.
Schritt 4: Bedingter Gaußprozess bei bekannten Stützpunkten
Ist der Gaußprozess eines Systems wie oben bestimmt worden, sind also Erwartungswertfunktion und Kovarianzfunktion bekannt, kann mit dem Gaußprozess eine Vorhersage beliebiger interpolierter Zwischenwerte berechnet werden, wenn nur wenige Stützstellen der gesuchten Funktion durch Messwerte bekannt sind. Die Vorhersage erfolgt durch die bedingte Wahrscheinlichkeit einer mehrdimensionalen Gaußverteilung bei einer gegebenen Teilinformation. Die Dimensionen der mehrdimensionalen Gaußverteilung
werden dabei unterteilt in unbekannte Werte, die vorhergesagt werden sollen
(Index U für unbekannt) und in bekannte Messwerte (Index B für bekannt).
Vektoren zerfallen dadurch in zwei Teile. Die Kovarianzmatrix wird entsprechend
in vier Blöcke unterteilt: Kovarianzen innerhalb der unbekannten Werte (UU),
innerhalb der bekannten Messwerte (BB) und Kovarianzen zwischen den unbekannten
und bekannten Werten (UB und BU). Die Werte der Kovarianzmatrix werden an
diskreten Stellen der Kovarianzfunktion abgelesen und der Erwartungswertvektor
an entsprechenden Stellen der Erwartungswertfunktion:
bzw.
Durch die Berücksichtigung der bekannten Messwerte
verändert sich die Verteilung zur bedingten bzw.
A-posteriori-Normalverteilung
,
wobei
die gesuchten unbekannten Variablen sind. Die Notation
bedeutet „bedingt durch
“.
Der erste Parameter der resultierenden Gaußverteilung beschreibt den neuen gesuchten Erwartungswertvektor, der jetzt den wahrscheinlichsten Funktionswerten der Interpolation entspricht. Zusätzlich wird im zweiten Parameter die vollständige vorhergesagte neue Kovarianzmatrix gegeben. Diese enthält insbesondere die Vertrauensintervalle der vorhergesagten Erwartungswerte, gegeben durch die Wurzel der Hauptdiagonalelemente.
Messrauschen und andere Störsignale
Weißes Messrauschen der Varianz
kann als Teil des A-Priori-Kovarianzmodells modelliert werden, indem der
Diagonale von
entsprechende Terme hinzugefügt werden. Wird mit derselben Kovarianzfunktion
auch die Matrix
gebildet, würden auch die vorhergesagte Verteilung ein weißes Rauschen der
Varianz
beschreiben. Um eine Vorhersage eines unverrauschten Signals zu erhalten, werden
in der A-posteriori-Verteilung
bei
und gegebenenfalls in
und
die entsprechenden Terme weggelassen. Dadurch wird das Messrauschen so gut wie
möglich weggemittelt, was auch im vorhergesagten Vertrauensintervall korrekt
berücksichtigt wird. Auf die gleiche Weise kann jegliches unerwünschte additive
Störsignal von den Messdaten entfernt werden (siehe auch Rechenoperation Zerlegung),
sofern es sich mit einer Kovarianzfunktion beschreiben lässt und sich vom
Nutzsignal hinreichend gut unterscheidet. Dazu wird anstelle der Diagonalmatrix
die entsprechende Kovarianzmatrix der Störung
eingesetzt. Messungen mit Störsignalen benötigen also zwei Kovarianzmodelle:
für das zu schätzende Nutzsignal und
für das Rohsignal.
Herleitung der bedingten Verteilung
Die Herleitung kann über die Bayes-Formel erfolgen, indem die beiden Wahrscheinlichkeitsdichten für bekannte und unbekannte Stützstellen sowie die Verbundwahrscheinlichkeitsdichte eingesetzt werden. Die resultierende bedingte A-posteriori-Normalverteilung entspricht dem Überlapp oder Schnittbild der Gaußverteilung mit dem durch die bekannten Werte aufgespannten Untervektorraum.
Bei verrauschten Messwerten, die selbst eine mehrdimensionale Normalverteilung darstellen, erhält man den Überlapp zur A-Priori-Verteilung durch die Multiplikation der beiden Wahrscheinlichkeitsdichten. Das Produkt der Wahrscheinlichkeitsdichten zweier mehrdimensionaler Normalverteilungen entspricht der Rechenoperationen Fusion, mit der die Verteilung bei unterdrücktem Störsignal hergeleitet werden kann.
A-posteriori Gaußprozess
In der vollständigen Darstellung als Gaußprozess ergibt sich aus dem A-priori-Gaußprozess
und den
bekannten Messwerten
an den Koordinaten
eine neue Verteilung, gegeben durch den bedingten
A-posteriori-Gaußprozess
mit
.
ist dabei eine Kovarianzmatrix, die sich durch die Auswertung der
Kovarianzfunktion
an den diskreten Zeilen
und Spalten
ergibt. Außerdem wurde
entsprechend als Vektor von Funktionen gebildet, indem
nur an diskreten Zeilen oder diskreten Spalten ausgewertet wurde.
In praktischen numerischen Berechnungen mit endlichen Zahlen von Stützstellen wird nur mit der Gleichung der bedingten mehrdimensionalen Normalverteilung gearbeitet. Die Notation des A-posteriori-Gaußprozesses dient hier nur dem theoretischen Verständnis, um den Grenzwert zum Kontinuum in Form von Funktionen zu beschreiben und damit die Zuordnung der Werte zu den Koordinaten darzustellen.
Schritt 5: Interpretation
Aus dem A-priori-Gaußprozess erhält man mit den Messwerten einen
A-posteriori-Gaußprozess, der die bekannte Teilinformation berücksichtigt.
Dieses Ergebnis der Gaußprozess-Regression repräsentiert nicht nur eine Lösung,
sondern die Gesamtheit aller möglichen und mit unterschiedlichen
Wahrscheinlichkeiten gewichteten Lösungsfunktionen der Interpolation. Die damit
ausgedrückte Unentschiedenheit ist keine Schwäche der Methode. Sie wird dem
Problem genau gerecht, da bei einer nicht vollständig bekannten Theorie oder bei
verrauschten Messwerten die Lösung prinzipiell nicht eindeutig bestimmbar ist.
Meist interessiert man sich jedoch speziell für diejenige Lösung mit der
zumindest höchsten Wahrscheinlichkeit. Diese ist durch die
Erwartungswertfunktion
im ersten Parameter des A-posteriori-Gaußprozesses gegeben. Aus der bedingten
Kovarianzfunktion im zweiten Parameter lässt sich die Streuung um diese Lösung
ablesen. Die Diagonale
der Kovarianzfunktion gibt eine Funktion mit den Varianzen der vorhergesagten
wahrscheinlichsten Funktion wieder. Das Vertrauensintervall ist dann durch die
Grenzen
gegeben.
Beispiele
- A-priori- und A-posteriori-Gaußprozesse
-
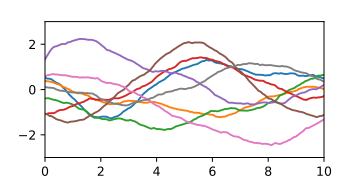 A-priori-Gaußprozess, dargestellt durch damit erzeugte Zufallskurven.
A-priori-Gaußprozess, dargestellt durch damit erzeugte Zufallskurven. -
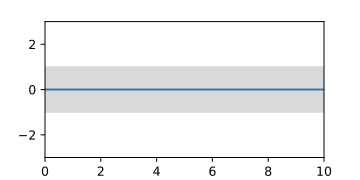 A-priori-Gaußprozess, dargestellt durch die Erwartungswertfunktion und die Fläche des Vertrauensintervalls.
A-priori-Gaußprozess, dargestellt durch die Erwartungswertfunktion und die Fläche des Vertrauensintervalls. -
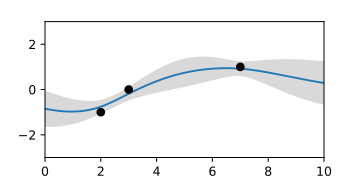
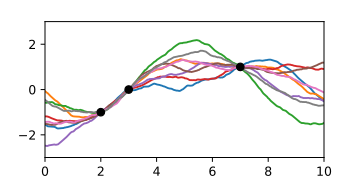 A-posteriori-Gaußprozess bei Kenntnis von drei Stützpunkten, dargestellt durch Zufallskurven.
A-posteriori-Gaußprozess bei Kenntnis von drei Stützpunkten, dargestellt durch Zufallskurven. -
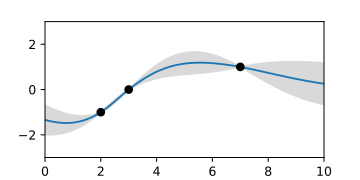 A-posteriori-Gaußprozess, dargestellt durch die Erwartungswertfunktion und Fläche des Vertrauensintervalls.
A-posteriori-Gaußprozess, dargestellt durch die Erwartungswertfunktion und Fläche des Vertrauensintervalls. -
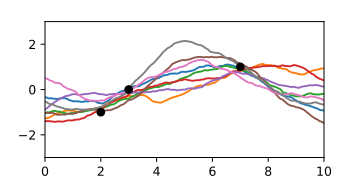 A-posteriori-Gaußprozess bei angenommenem Messrauschen. Die Interpolationen treffen die Punkte nicht mehr exakt.
A-posteriori-Gaußprozess bei angenommenem Messrauschen. Die Interpolationen treffen die Punkte nicht mehr exakt. -
 A-posteriori-Gaußprozess bei angenommenem Messrauschen. Der Erwartungswert wird glatter und das Vertrauensintervall bleibt größer Null.
A-posteriori-Gaußprozess bei angenommenem Messrauschen. Der Erwartungswert wird glatter und das Vertrauensintervall bleibt größer Null. -
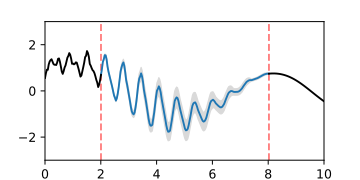 A-posteriori-Gaußprozess der Interpolation einer Lücke, dargestellt durch die Erwartungswertfunktion und Fläche des Vertrauensintervalls
A-posteriori-Gaußprozess der Interpolation einer Lücke, dargestellt durch die Erwartungswertfunktion und Fläche des Vertrauensintervalls -
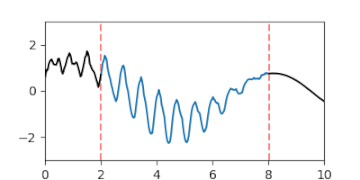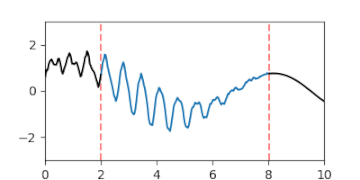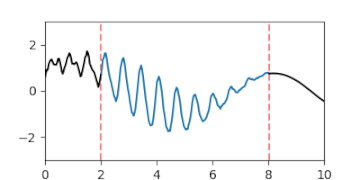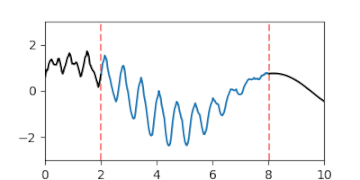 A-posteriori-Gaußprozess der Interpolation einer Lücke, dargestellt durch animierte Zufallsfluktuationen gemäß der Verteilung.
A-posteriori-Gaußprozess der Interpolation einer Lücke, dargestellt durch animierte Zufallsfluktuationen gemäß der Verteilung.
Sonderfälle
Unterbestimmte Messwerte
In manchen Fällen von bedingten Gaußprozessen sind Gruppen von linear
zusammenhängenden Messwerten vollständig unbestimmt, z.B. bei indirekten
Messwerten, die aus unterbestimmten Gleichungen folgen, etwa mit einer nicht
invertierbaren positiv semidefiniten Matrix der Form .
Die Stützstellen lassen sich dann nicht einfach in bekannte und unbekannte Werte
aufteilen und die zugehörige Kovarianzmatrix wäre aufgrund unendlicher
Unsicherheiten singulär. Das entspräche einer Normalverteilung, die in bestimmte
Raumrichtungen quer zu den Koordinatenachsen unendlich ausgedehnt ist. Um die
Beziehungen zwischen den unbestimmten Variablen zu berücksichtigen, muss in
einem solchen Fall mit der inversen Matrix
,
der sogenannten Präzisionsmatrix,
gerechnet werden. Diese kann vollständig unbestimmte Messwerte beschreiben, was
durch Nullen in der Diagonale ausgedrückt wird. Für eine solche Verteilung
mit teilweise unbekannten Messwerten
und singulären Messunsicherheiten
wird die gesuchte A-posteriori-Verteilung durch den Überlapp zum
A-priori-Gaußprozess-Modell
berechnet, indem die Wahrscheinlichkeitsdichten multipliziert werden. Die
Vereinigung der beiden Normalverteilungen
gemäß der Operation Fusion ergibt immer eine endliche Normalverteilung, da eine der beiden endlich ist. Sind beide Eingangsverteilungen endlich, dann ist das Ergebnis identisch zur A-posteriori-Verteilung, die man mit der Formel für die bedingte Verteilung erhält.
Linearkombination zu einem Gaußprozess
Aus gegebenen Basisfunktionen
soll eine Linearkombination gebildet werden, die mit der Verteilung
eines zugehörigen Gaußprozesses
maximalen Überlapp hat. Oder es sollen Messwerte
approximiert werden, während das darin enthaltene Störsignal
möglichst ignoriert wird. In beiden Fällen können die gesuchten Koeffizienten
mit der verallgemeinerten
Kleinste-Quadrate-Schätzung
berechnet werden. Dabei enthält die Matrix
die Funktionswerte der Basisfunktionen
an den Stützstellen
.
Die resultierenden Koeffizienten c mit der zugehörigen Kovarianzmatrix
beschreiben diejenige Linearkombination mit der größtmöglichen
Wahrscheinlichkeitsdichte in der Verteilung
.
Die Linearkombination approximiert dabei die Erwartungswertfunktion oder die
Messwerte
auf eine solche Weise, dass die Residuen bestmöglich durch die Kovarianzmatrix
beschrieben werden.
Approximation eines empirischen Gaußprozesses
Ein aus Beispielfunktionen
empirisch bestimmter Gaußprozess
mit wenigen stark ausgeprägten Freiheitsgraden kann mittels einer Eigenwertzerlegung oder der Singulärwertzerlegung
der Kovarianzmatrix
approximiert und vereinfacht werden. Dazu wählt man die
größten Eigenwerte bzw. Singulärwerte
aus der Diagonalmatrix
.
Die zugehörigen Spalten
von
sind die Hauptkomponenten des Gaußprozesses (siehe
Hauptkomponentenanalyse).
Stellt man die Spalten als Funktionen
dar, dann wird der ursprüngliche Gaußprozess durch die Mittelwertfunktion
und die Kovarianzfunktion
approximiert. Dieser Gaußprozess beschreibt ausschließlich Funktionen der Linearkombination
,
wobei jeder Koeffizient
als unabhängige Zufallsvariable der Varianz
um den Mittelwert Null gestreut wird.
Eine solche Vereinfachung ist positiv semidefinit und ihr fehlen meist die Eigenschaften zur Beschreibung kleinskaliger Variationen. Diese Eigenschaften können der Kovarianzfunktion in Form einer an die Residuen angepassten stationären Kovarianzfunktion hinzugefügt werden:
Zeitlicher Gauß-Markov-Prozess
Bei Kovarianzfunktionen mit sehr vielen räumlichen und zeitlichen Stützpunkten können sehr große und rechenintensive Kovarianzmatrizen entstehen. Wenn sich in einem solchen Fall die stationäre Zeitabhängigkeit mittels Gauß-Markov-Prozess beschreiben lässt (exponentiell abfallende Kovarianzfunktion), dann kann das Schätz-Problem effizient durch einen iterativen Ansatz mithilfe des Kalman-Filters gelöst werden.
Gaußprozesse mit linearen Nebenbedingungen
Im Falle vieler interessanter Anwendungen ist bereits im Vorhinein Wissen über das Verhalten des betrachteten Systems vorhanden. Man betrachte zum Beispiel den Fall, in dem der Gaußprozess ein Magnetfeld beschreiben soll; hier gehorcht dann das echte Magnetfeld den Maxwell-Gleichungen und es wäre vorteilhaft, dieses Wissen auch in den Gaußprozess zu inkludieren, da dies höchstwahrscheinlich dessen Vorhersagekraft verbessern würde.
Es gibt bereits eine Methode, um lineare Nebenbedingungen in den Formalismus des Gaußprozesses miteinzubeziehen:
Betrachte die (vektorwertige) Funktion ,
die bekanntermaßen der linearen Nebenbedingung (d.h.
ist ein linearer Operator)
gehorcht. Dann kann die Nebenbedingung
erfüllt werden, indem man
wählt (wobei es sich bei
um einen Gaußprozess handelt) und anschließend
bestimmt, sodass
Mit gegebenem
und unter Verwendung der Tatsache, dass Gaußprozesse abgeschlossen unter
linearen Transformationen sind, kann der Gaußprozess für
,
der der Nebenbedingung
gehorcht, geschrieben werden als
Somit können lineare Nebenbedingungen im Mittelwert und der Kovarianzfunktion des Gaußprozesses berücksichtigt werden.
Anwendungsbeispiele
Beispiel: Trend-Vorhersage
In einem Anwendungsbeispiel aus der Marktforschung soll die zukünftige Nachfrage zum Thema "Snowboard" vorhergesagt werden. Dazu soll eine Extrapolation der Anzahl von Google-Suchanfragen[3] zu diesem Begriff berechnet werden.
In den vergangenen Daten erkennt man eine periodische, jedoch nicht sinusförmige Jahreszeitabhängigkeit, die durch den Winter auf der Nordhalbkugel zu erklären ist. Außerdem nahm der Trend über das letzte Jahrzehnt kontinuierlich ab. Zusätzlich erkennt man eine wiederkehrende Erhöhung der Suchanfragen während der olympischen Spiele alle vier Jahre. Die Kovarianzfunktion wurde daher mit einem langsamen Trend sowie einer ein- und vierjährigen Periode modelliert:
Der Trend scheint eine deutliche Asymmetrie aufzuweisen, was der Fall sein kann, wenn sich die zugrundeliegenden Zufallseffekte nicht addieren, sondern gegenseitig verstärken, was eine Log-Normal-Verteilung zur Folge hat. Der Logarithmus solcher Werte beschreibt jedoch eine Normalverteilung, worauf die Gaußprozess-Regression angewendet werden kann.
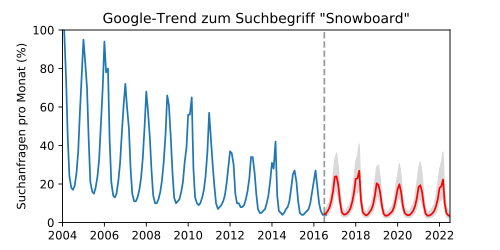
Die Abbildung zeigt eine Extrapolation der Kurve (rechts der gestrichelten Linie). Da die Ergebnisse hier mit einer Exponentialfunktion aus der logarithmischen Darstellung zurücktransformiert wurden, sind die vorhergesagten Vertrauensintervalle entsprechend asymmetrisch (graue Fläche). Die Extrapolation zeigt sehr plausibel die saisonalen Verläufe und sagt sogar die Erhöhung der Suchanfragen bei den Olympischen Spielen voraus.
Dieses Beispiel mit gemischten Eigenschaften zeigt deutlich die Universalität der Gaußprozess-Regression gegenüber anderen Interpolationsverfahren, die meist auf spezielle Eigenschaften optimiert sind.
Beispiel: Sensorkalibrierung
In einem Anwendungsbeispiel aus der Industrie sollen mithilfe von
Gaußprozessen Sensoren kalibriert werden.
Aufgrund von Toleranzen bei der Herstellung zeigen die Kennlinien
der Sensoren große individuelle Unterschiede. Das verursacht hohe Kosten bei der
Kalibrierung, da für jeden Sensor eine vollständige Kennlinie gemessen werden
müsste. Der Aufwand kann jedoch minimiert werden, indem das genaue Verhalten der
Streuung durch einen Gaußprozess erlernt wird. Dazu werden von
zufällig ausgewählten repräsentativen Sensoren die vollständigen Kennlinien
gemessen und damit der Gaußprozess
der Streuung durch
berechnet. Im gezeigten Beispiel sind 15 repräsentative Kennlinien gegeben.
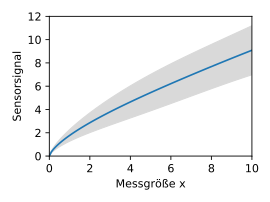
Der daraus resultierende Gaußprozess ist durch die Mittelwertfunktion
und das Vertrauensintervall
dargestellt.
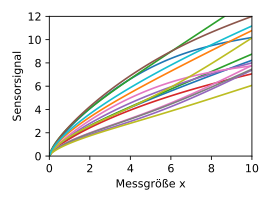
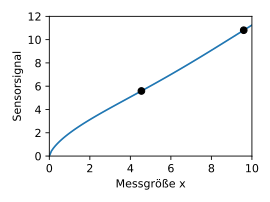
Mit dem bedingten Gaußprozess
mit
kann nun für jeden neuen Sensor mit wenigen einzelnen Messwerten
an den Koordinaten
das vollständige Kennfeld rekonstruiert werden. Die Anzahl von Messwerten muss
dabei mindestens der Anzahl der Freiheitsgrade der Toleranzen entsprechen, die
einen unabhängigen linearen Einfluss auf die Form der Kennlinie haben.
Im dargestellten Beispiel genügt ein einzelner Messwert noch nicht, um die Kennlinie eindeutig und präzise zu bestimmen. Das Vertrauensintervall zeigt den Bereich der Kurve, der noch nicht ausreichend genau ist. Mit einem weiteren Messwert in diesem Bereich kann schließlich die verbleibende Unsicherheit vollständig eliminiert werden. Die Exemplarschwankungen der sehr unterschiedlich wirkenden Sensoren in diesem Beispiel scheinen also durch die Toleranzen von nur zwei relevanten inneren Freiheitsgraden verursacht zu werden.
Beispiel: Signalzerlegung
In einem Anwendungsbeispiel aus der Signalverarbeitung soll ein zeitliches Signal in seine Bestandteile zerlegt werden. Über das System sei bekannt, dass das Signal aus drei Komponenten besteht, die den drei Kovarianzfunktionen
folgen. Das Summensignal folgt dann nach der Additionsregel der Kovarianzfunktion
.
Die folgenden beiden Abbildungen zeigen drei Zufallssignale, die zur Demonstration mit diesen Kovarianzfunktionen erzeugt und addiert wurden. In der Summe der Signale kann man mit bloßem Auge kaum das darin verborgene periodische Signal erkennen, da dessen Spektralbereich mit dem der beiden anderen Komponenten überlappt.
-
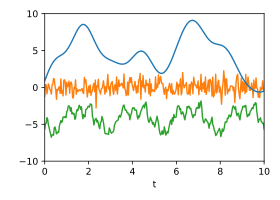 Einzelsignale: Drei zufällig erzeugte Signale, die bestimmten Gaußprozessen folgen.
Einzelsignale: Drei zufällig erzeugte Signale, die bestimmten Gaußprozessen folgen. -
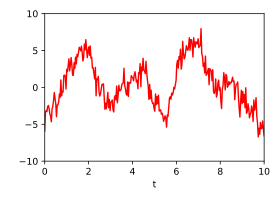 Summe: Die Summe der drei Signale.
Summe: Die Summe der drei Signale.
Mithilfe der Operation Zerlegung
kann die Summe
wieder in die drei Komponenten
zerlegt werden, wobei .
Die Schätzung der wahrscheinlichsten Zerlegung zeigt, wie gut die Trennung in
diesem Fall möglich ist und wie nah die Signale an den ursprünglichen Signalen
liegen. Die geschätzten Unsicherheiten unter Berücksichtigung der
Kreuzkorrelationen sind in der Animation durch Zufallsfluktuationen dargestellt.
-
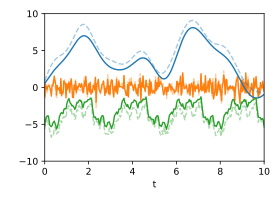 Zerlegung: Wahrscheinlichste Zerlegung bei Kenntnis der jeweiligen Kovarianzfunktionen. Die ursprünglichen Signale sind gestrichelt dargestellt.
Zerlegung: Wahrscheinlichste Zerlegung bei Kenntnis der jeweiligen Kovarianzfunktionen. Die ursprünglichen Signale sind gestrichelt dargestellt. -
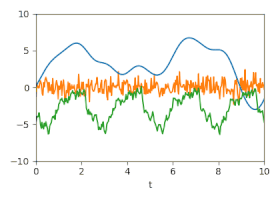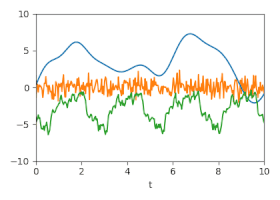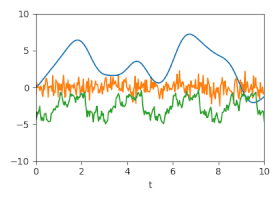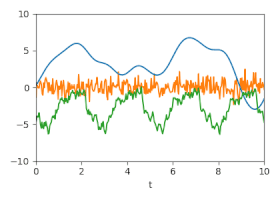 Unsicherheit: Geschätzte Unsicherheiten dargestellt durch animierte Zufallsfluktuationen entsprechend der (Kreuz-)Kovarianzmatrizen.
Unsicherheit: Geschätzte Unsicherheiten dargestellt durch animierte Zufallsfluktuationen entsprechend der (Kreuz-)Kovarianzmatrizen.
Das Beispiel zeigt, wie mit diesem Verfahren sehr verschiedenartige Signale in einem Schritt getrennt werden können. Andere Filterverfahren wie gleitende Mittelung, Fourierfilterung, Polynomregression oder Splineapproximation sind dagegen auf spezielle Signaleigenschaften optimiert und liefern weder genaue Fehlerschätzungen noch Kreuzkorrelationen.
Sind die Gaußprozesse der Einzelkomponenten für ein gegebenes Signal nicht genau bekannt, dann kann in manchen Fällen eine Hypothesenprüfung mithilfe der Log-Marginal-Likelihood-Funktion durchgeführt werden, sofern hinreichend viele Daten für eine gute Konditionierung der Funktion zur Verfügung stehen. Über deren Maximierung können die Parameter der vermuteten Kovarianzfunktionen an die Messdaten angepasst werden.
Anmerkungen
- ↑
Die Herleitung der allgemeinen linearen
Transformation erfolgt aus der Gleichung
, indem die Matrix F als [A B] gewählt wird,
als Vektor (
) und
aus entsprechenden vier Blöcken.
- ↑
Die Herleitung erfolgt mit der Kovarianz-Regel
für Multiplikation
und Assoziativität
.
- ↑
Die Daten sind erhältlich bei
 Google-Trends
zum Suchbegriff "Snowboard".
Google-Trends
zum Suchbegriff "Snowboard".


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 07.04. 2023