
Operatortopologie
Operatortopologien werden im mathematischen Teilgebiet der Funktionalanalysis untersucht. Es handelt sich um verschiedene Topologien auf dem Raum der stetigen, linearen Operatoren auf einem Hilbertraum.
Diese Topologien sind besonders für unendlichdimensionale Hilberträume von
großem Interesse, da sie für endlichdimensionale Hilberträume mit der Normtopologie
zusammenfallen und dort somit entbehrlich sind. Daher sei im Folgenden
stets ein unendlichdimensionaler Hilbertraum und
bezeichne die Algebra der stetigen linearen Operatoren auf
.
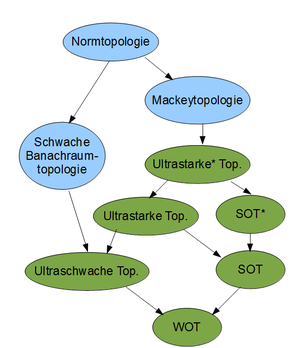
Normtopologie
Die Operatornorm, die jedem
Operator
den Wert
zuordnet, definiert eine Normtopologie auf .
Sie macht
zu einer Banachalgebra,
mit der Adjunktion
als Involution zu einer C*-Algebra,
sogar von-Neumann-Algebra.
Neben dieser Normtopologie wird zur Untersuchung von
bzw. darin enthaltenen Operatoralgebren
eine Reihe weiterer sogenannter Operatortopologien herangezogen. Es handelt sich
dabei jeweils um lokalkonvexe
Topologien, die im Folgenden durch eine definierende Familie
von Halbnormen beschrieben werden.
Ein Netz
von Operatoren konvergiert in dieser Topologie genau dann gegen ein
,
wenn
für alle
.
Schwache Topologie
Halbnormen
Wie jeder Banachraum
trägt auch
eine schwache
Topologie. Diese ist durch das System der Halbnormen
gegeben. Dabei ist
der Dualraum von
.
Anmerkung
Da man die stetigen, linearen Funktionale auf
(im Allgemeinen) nicht gut beschreiben kann und da die Einheitskugel in
bzgl. der schwachen Topologie wegen fehlender Reflexivität
nicht kompakt
ist, spielt diese Topologie nur eine untergeordnete Rolle. Viele Autoren meinen
mit schwacher Topologie daher auch die unten vorgestellte schwache
Operatortopologie.
Starke Operatortopologie
Halbnormen
Die starke Operatortopologie (engl. SOT = strong operator topology) ist die Topologie der punktweisen Normkonvergenz, sie wird durch die Halbnormen
erzeugt.
Eigenschaften
Die Multiplikation
ist nicht SOT-stetig. Die Multiplikation wird SOT-stetig, wenn der linke Faktor
beschränkt bleibt. Insbesondere ist die Multiplikation SOT-folgenstetig, denn
jede SOT-konvergente Folge ist nach dem Satz von
Banach-Steinhaus beschränkt.
Die Involution
ist nicht SOT-stetig. Ist zum Beispiel
der unilaterale
Shiftoperator, so ist
bzgl. SOT, aber die Folge
konvergiert nicht in SOT gegen 0. Aber die Einschränkung der Involution auf die
Menge aller normalen
Operatoren ist SOT-stetig.
Die abgeschlossenen Normkugeln sind SOT-vollständig,
ist SOT-quasivollständig
und SOT-folgenvollständig.
Die Einheitskugel ist nicht SOT-kompakt (
unendlichdimensional, wie in diesem Artikel angenommen).
Schwache Operatortopologie
Halbnormen
Die schwache Operatortopologie (engl. WOT = weak operator topology) ist die Topologie der punktweisen schwachen Konvergenz, das heißt, sie ist durch die Halbnormen
definiert.
Eigenschaften
Die Multiplikation
ist nicht WOT-stetig, hingegen sind die einseitigen Multiplikationen, das heißt
die Abbildungen
und
für festes
,
WOT-stetig.
Die Involution
ist WOT-stetig.
Die wohl wichtigste Eigenschaft ist die WOT-Kompaktheit der Einheitskugel und
damit jeder Kugel mit endlichem Radius. Ist
separabel, so sind die
Kugeln zusätzlich metrisierbar.
Die WOT-stetigen linearen Funktionale auf
sind genau die Funktionale der Form
für endliches
und
.
Das sind auch genau die SOT-stetigen Funktionale, weshalb sich aus dem
Trennungssatz ergibt, dass die WOT-Abschlüsse und SOT-Abschlüsse konvexer Mengen
übereinstimmen.
Starke *-Operatortopologie
Halbnormen
Nach Obigem ist die Involution stetig bzgl. WOT und bzgl. der Normtopologie, nicht aber für die dazwischen liegende SOT. Diesem Mangel kann durch Übergang zur starken*-Operatortopologie SOT* begegnet werden. Dazu betrachtet man die Topologie, die durch die Halbnormen
erzeugt wird.
Eigenschaften
Ist
und bezeichnet
die Kugel um 0 mit Radius
in
,
so ist die eingeschränkte Multiplikation
SOT*-stetig. Nach Konstruktion ist auch die Involution SOT*-stetig.
Ferner ist ein lineares Funktional auf
genau dann SOT*-stetig, wenn es WOT-stetig ist.
Ultraschwache Topologie
Halbnormen
Die ultraschwache Topologie, von manchen Autoren auch -schwache
Topologie genannt, ist die schwach-*-Topologie
der Dualität
,
wobei
der Raum der Spurklasseoperatoren
sei und die Dualität bekanntlich durch
gegeben ist. Die Topologie wird durch die Halbnormen
Folgen in
mit
,
erzeugt.
Eigenschaften
Da es sich um eine schwach-*-Topologie handelt, ist die Einheitskugel nach
dem Satz
von Banach-Alaoglu ultraschwach kompakt. Sie stimmt auf jeder beschränkten
Menge mit der WOT überein, ist aber auf
echt feiner als WOT.
Wie bei der WOT sind die Involution und die einseitigen Multiplikationen ultraschwach stetig.
Für beschränkte Funktionale
auf
sind folgende Aussagen äquivalent:
ist ultraschwach stetig
- Die Einschränkung von
auf die Einheitskugel ist WOT-stetig
- Es gibt einen Spurklasseoperator
mit
für alle
- Ist
ein beschränktes und monoton wachsendes Netz selbstadjungierter Operatoren mit Supremum
, so ist
.
Ultrastarke Topologie
Halbnormen
Die hier zu definierende ultrastarke Topologie, die auch unter dem Namen
-starke
Topologie bekannt ist, steht zur ultraschwachen Topologie in einem analogen
Verhältnis wie sie SOT zur WOT. Die definierenden Halbnormen sind
Folge in
mit
.
Eigenschaften
Wie bei der SOT ist die Multiplikation nicht ultrastark stetig, sie wird aber ultrastark-stetig, wenn der linke Faktor beschränkt bleibt. Die Involution ist nicht ultrastark-stetig.
Die ultrastarke Topologie stimmt auf jeder beschränkten Menge mit der SOT
überein, ist aber auf
echt feiner als SOT.
Die ultrastark-stetigen linearen Funktionale auf
stimmen mit den ultraschwach-stetigen linearen Funktionalen überein,
insbesondere haben konvexe Mengen übereinstimmende ultrastarke und ultraschwache
Abschlüsse.
Ultrastarke*-Topologie
Halbnormen
In Analogie zur SOT* wird sie ultrastarke*-Topologie durch folgendes System von Halbnormen definiert:
Folge in
mit
.
Eigenschaften
Die ultrastarke*-Topologie stimmt auf beschränkten Mengen mit der
SOT*-Topologie überein, die eingeschränkte Multiplikation
ist ultrastark*-stetig, ebenso ist definitionsgemäß die Involution
ultrastark*-stetig.
Ferner ist ein lineares Funktional auf
genau dann ultrastark*-stetig, wenn es ultraschwach stetig ist.
Auf beschränkten Mengen stimmen die SOT* und die ultrastarke* Topologie mit der Mackey-Topologie überein, letztere ist die feinste lokalkonvexe Topologie, die dieselben stetigen linearen Funktionale hat wie die ultraschwache Topologie.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 05.09. 2022