
Singuläre Homologie
Die Singuläre Homologie ist eine Methode der algebraischen Topologie, die einem beliebigen topologischen Raum eine Folge abelscher Gruppen zuordnet. Anschaulich gesprochen zählt sie die verschieden-dimensionalen Löcher eines Raumes. Gegenüber den ähnlich gearteten Homotopiegruppen hat die singuläre Homologie den Vorteil, dass sie wesentlich einfacher zu berechnen ist und somit für viele Anwendungen die effektivste algebraische Invariante darstellt. Definiert ist sie als die Homologie zum singulären Kettenkomplex.
Simpliziale Homologie
Die historischen Wurzeln der singulären Homologie liegen in der simplizialen
Homologie. Sei hierzu
ein simplizialer
Komplex, das heißt eine Menge
von Simplizes,
so dass jede Seitenfläche eines der Simplizes wieder in dieser Menge liegt.
Einfache Beispiele sind Polygone
und Polyeder. Nach einem Satz der
Topologie
kann man jede differenzierbare
Mannigfaltigkeit triangulieren, also als einen simplizialen Komplex (SK)
auffassen.
Das Ziel ist nun, aus diesem simplizialen Komplex einen Kettenkomplex zu machen,
von dem man dann die Homologie
nimmt. Hierzu sei
die freie
abelsche Gruppe über der Menge der
-Simplizes
des simplizialen Komplexes. Die Randabbildung
in SK bildet jeden Simplex auf die alternierende Summe seiner Seitenflächen ab,
das heißt
wobei die alternierenden Vorzeichenfaktoren auch als „geometrische Orientierungsgrößen“ interpretiert werden können.
Die Homologie dieses Kettenkomplexes heißt dann die simpliziale Homologie
von .
Geschichtlicher Überblick
Die Definition der simplizialen Homologie hat zwei wesentliche Probleme. Das eine ist, dass nicht jeder topologische Raum eine Darstellung als simplizialer Komplex hat. Das zweite und gewichtigere ist, dass der gleiche Raum zwei verschiedene Darstellungen als simplizialer Komplex haben kann und damit a priori die simpliziale Homologie keine topologische Invariante des Raumes darstellt. Historisch war der erste Lösungsversuch zu diesem Problem die sogenannte Hauptvermutung, die Ernst Steinitz und Heinrich Tietze zu Beginn des 20. Jahrhunderts aufstellten. Diese besagt, dass zwei Triangulierungen eines Raums immer eine gemeinsame Verfeinerung besitzen. Die Hauptvermutung wurde jedoch 1961 von John Willard Milnor widerlegt.
Die Lösung des Problems nahm jedoch schon in den Dreißigern und Vierzigern durch die Arbeiten von Solomon Lefschetz und Samuel Eilenberg Gestalt an. Sie definierten die singuläre Homologie. Diese ist im Grundgedanken ähnlich wie die simpliziale Homologie, nimmt jedoch als ihren Kettenkomplex sogenannten singulären Kettenkomplex.
Definition
Singulärer Kettenkomplex
Sei
ein topologischer
Raum und
ein
-(euklidischer)
Simplex, ein singulärer
-Simplex
in
ist eine stetige
Abbildung
.
Mit
wird die freie
abelsche Gruppe, die durch die Menge aller singulären
-Simplizes
in
erzeugt wird, bezeichnet. Ein Element von
ist also eine formale Linearkombination
von singulären Simplizes und wird singuläre
-Kette
genannt. Die Gruppe
heißt singuläre Kettengruppe der Dimension
.
Für ein
wird durch
ein Homomorphismus
definiert. Dies ergibt einen Randoperator,
das heißt, es gilt
.
Somit ist
ein Kettenkomplex, der singulärer Kettenkomplex genannt wird.
Singuläre Homologie
Die Homologie
dieses Kettenkomplexes nennt man singuläre Homologie von
oder auch schlicht die Homologie von
und man bezeichnet die Homologiegruppen
auch präzise als die singulären Homologiegruppen. Für jeden simplizialen Komplex ist sie isomorph zur simplizialen Homologie.
Die Elemente von
werden als Homologieklassen bezeichnet.
Reduzierte Homologie
In vielen Sätzen der Homologietheorie spielt die 0-te Homologe
eine Sonderrolle, weshalb es für eine einheitliche Formulierung von Sätzen und
Beweisen oft nützlich ist, die reduzierte Homologie
zu betrachten. Diese ist definiert durch
für alle
und
,
wobei
die durch
definierte Augmentierung des Kettenkomplexes
ist. Es gilt
.
Relative Homologie und Abbildungen
Man kann die singuläre Homologie nicht nur von einem Raum ,
sondern auch von einem Raumpaar
,
d.h. von einem Raum
und einem in ihm enthaltenen Raum
bilden. Hierzu setzt man den Kettenkomplex
gleich der Faktorgruppe
,
die Definition der Randabbildung
bleibt. Die Homologie dieses Kettenkomplexes bezeichnet man als die relative
Homologiegruppe
.
Anschaulich gesprochen will man das Innere von
ignorieren, wie es im nächsten Abschnitt noch in der Ausschneidungseigenschaft
präzisiert wird. Es gilt
.
Jede Abbildung zwischen zwei Raumpaaren induziert auch einen Gruppenhomomorphismus
der entsprechenden Homologiegruppen. Sei dazu
eine stetige
Abbildung zwischen zwei Raumpaaren, d.h. eine stetige Abbildung von
nach
,
so dass
.
Diese Abbildung
definiert eine Kettenabbildung von
nach
,
indem sie jedem singulären Simplex
den singulären Simplex
zuordnet. Dadurch bekommt man eine Abbildung
.
So erhält man, dass jedes
ein kovarianter Funktor
von der Kategorie
der Raumpaare in die Kategorie der abelschen Gruppen ist.
Eigenschaften
Mit Mitteln der homologischen Algebra kann man zeigen, dass stets eine lange exakte Sequenz von Homologiegruppen existiert:
Die Abbildungen
und
sind dabei von der Inklusion bzw. der Projektion induziert. Die Abbildung
ist ein über das Schlangenlemma
definierter Randoperator
.
Eine weitere wichtige Eigenschaft von
ist seine Homotopieinvarianz. Seien
dazu
zwei stetige Abbildungen, die homotop
sind. Dann besagt der sogenannte Homotopiesatz:
Die induzierten Gruppenhomomorphismen
sind identisch. So sind insbesondere die Homologiegruppen von zwei homotopieäquivalenten
Räumen isomorph.
Für relative Homologiegruppen gilt die Ausschneidungseigenschaft. Sei hierzu
ein Raumpaar und
,
so dass der Abschluss
von
im Inneren von
enthalten ist. Dann ist die von der Inklusion induzierte Abbildung
ein Isomorphismus.
Damit sind die sogenannten Eilenberg-Steenrod-Axiome
erfüllt und es ist gezeigt, dass die singuläre Homologie eine Homologietheorie ist.
Damit gelten für die singuläre Homologie auch alle Eigenschaften, die ganz
allgemein für alle Homologietheorien gelten. Das sind insbesondere die Mayer-Vietoris-Sequenz
und der Einhängungsisomorphismus, der besagt, dass .
Hierbei bezeichnet
die Einhängung von
.
Für eine n-dimensionale Mannigfaltigkeit
gilt, dass
für
.
Allgemeiner gilt dies auch für einen CW-Komplex, der keine Zellen
der Dimension größer als
hat.
Beispiele und Berechnung
Das einfachste Beispiel ist die Homologie eines Punktes. Es gibt für jeden
Simplex
nur eine Abbildung in den Raum, womit der Kettenkomplex die folgende Gestalt
annimmt:
Hierbei sind die Randabbildung immer abwechselnd die 0 und die Identität, so
dass der vorletzte Pfeil die Nullabbildung
ist. Es gilt somit
für jedes n > 0 und
.
Wegen der Homotopieinvarianz gilt selbiges für jeden zusammenziehbaren Raum.
Im Allgemeinen nützt eine direkte Betrachtung des singulären Kettenkomplexes
allerdings wenig, da dieser im Normalfall in jeder positiven Dimension
unendlich-dimensional ist. Eine Methode der Berechnung beruht auf den oben
erwähnten Eigenschaften der singulären Homologie. So kann man beispielsweise mit
Hilfe des Einhängungsisomorphismus und der langen exakten Sequenz des Raumpaares
berechnen, dass für
für
oder
,
für
und
sonst.
Ein weiteres Beispiel, das man mit Methoden der zellulären
Homologie berechnen kann, ist die Homologie des reell projektiven
Raums. Für
gerade:
Und für
ungerade:
Anwendungen
Eine klassische Anwendung ist der Brouwersche Fixpunktsatz. Dieser besagt, dass jede stetige Abbildung der n-dimensionalen Kugel Dn in sich selbst einen Fixpunkt besitzt. Der Beweis läuft per Widerspruch.
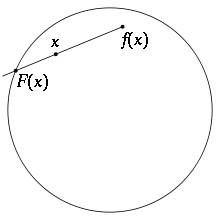
Angenommen, es existierte eine Abbildung ,
die keinen Fixpunkt hat. Dann kann man für jeden Punkt
den Strahl von
nach
zeichnen, der den Rand der Kugel in dem Punkt
trifft (wie im Bild angedeutet). Die Funktion
ist stetig und hat die Eigenschaft, dass jeder Punkt auf dem Rand auf sich
selbst abgebildet wird. Damit ist
gleich der Identität, wobei
die Inklusion des Randes in die Vollkugel ist. Damit ist auch die induzierte
Abbildung
gleich der Identität. Nun ist aber laut des vorherigen Abschnittes ,
allerdings
.
Damit haben wir den Widerspruch.
Weitere Anwendungen sind der Satz von Borsuk-Ulam und der 823: Nach dem Jordan-Brouwer-Zerlegungssatz, eine Verallgemeinerung des Jordanschen Kurvensatzes.
Koeffizienten und Bettizahlen
Bei der Konstruktion des singulären Kettenkomplexes wurde die freie abelsche
Gruppe, also der freie -Modul,
über alle singulären Simplizes gebildet. Die daraus entstehende Homologie
bezeichnet man auch als Homologie mit Koeffizienten in
.
Es ist allerdings auch möglich, eine beliebige andere abelsche
Koeffizientengruppe
zu wählen. Dies erreicht man, indem man den Kettenkomplex
mit
tensoriert. Die daraus
entstehende Homologie
bezeichnet man als die Homologie des Raumpaares
mit Koeffizienten in
.
Die Umrechnung von Homologie mit verschiedenen Koeffizientengruppen ineinander erfolgt üblicherweise mittels universellen Koeffiziententheoremen.
Eine besondere Rolle spielen Körper als Koeffizienten. Hier ist der Kettenkomplex in jeder Dimension ein Vektorraum und somit auch die entstehende Homologie. Auf diese Weise kann man auch die sogenannten Bettizahlen definieren:
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 19.10. 2021