Retraktion und Koretraktion

In der Kategorientheorie versteht man unter einer Retraktion einen Morphismus , der ein Rechtsinverses besitzt, das heißt, zu dem es einen Morphismus gibt mit $f\circ g=\operatorname {id}$ . Der duale Begriff einer Retraktion ist der der Koretraktion (oder Schnitt), das heißt ein Morphismus, der ein Linksinverses besitzt. Das Rechtsinverse einer Retraktion ist eine Koretraktion und umgekehrt.

Ein Objekt einer Kategorie ${\mathcal {C}}$ heißt Retrakt eines Objekts $Y\in {\mathcal {C}}$ , wenn es in ${\mathcal {C}}$ einen Morphismus $f\colon X\to Y$ und eine Retraktion $r\colon Y\to X$ zu , also einen Morphismus mit $r\circ f=\operatorname {id}_{X}$ , gibt.

Jede Retraktion ist ein extremer und sogar regulärer Epimorphismus. Ebenso ist jede Koretraktion extremer und sogar regulärer Monomorphismus und sogar Differenzkern.

Spezielle Kategorien

Topologische Räume

Der Begriff der Retraktion findet Anwendung in der algebraischen Topologie. In der Kategorie $\mathbf{Top}$ der topologischen Räume sind alle extremen Monomorphismen und damit auch alle Koretraktionen topologische Einbettungen. Dies ermöglicht im Falle topologischer Räume eine andere Sichtweise und Definition: Eine Retraktion ist ein stetiges Linksinverses einer topologischen Einbettung. Oder konkret formuliert: Eine Retraktion ist eine stetige Abbildung von einem topologischen Raum in sich selbst, sodass jedes Element der Bildmenge Fixpunkt ist.

Dies erlaubt auch eine konkrete Definition des Retrakts: Ein Teilraum eines topologischen Raums heißt Retrakt von , wenn es eine Retraktion zur Einbettung $i\colon A\to X$ gibt.

ist genau dann Retrakt von , wenn jede stetige Abbildung $f\colon A\to Y$ stetig zu einer Abbildung $g\colon X\to Y$ fortgesetzt werden kann:

Gibt es eine Retraktion $r\colon X\to A$ , so ist $g:=f\circ r$ stetige Fortsetzung.
Eine Fortsetzung von $\operatorname {id} _{A}$ zu einer stetigen Abbildung $r\colon X\to A$ ist eine Retraktion.

In einem Hausdorffraum ist jedes Retrakt abgeschlossen: Sei $A\subset X$ Retrakt mit Retraktion $r\colon X\to A$ . Betrachte nun ein konvergentes Netz $N_{i}\to a$ auf . Das Bildnetz $r(N_{i})$ konvergiert gegen r(a) (da stetig) und ist gleich dem ursprünglichen Netz. Da der Grenzwert eines Netzes in Hausdorffräumen eindeutig ist, gilt somit $r(a)=a\in A$ und ist abgeschlossen. In Nicht-Hausdorffräumen gilt dies nicht: In Nicht-T₁-Räumen existieren nicht-abgeschlossene einelementige Mengen, die aber offensichtlich Retrakte sind. Als Beispiel für einen T₁-Raum mit nicht-abgeschlossenem Retrakt betrachte die kofinite Topologie auf $\mathbb {N}$ : $r\colon \mathbb{N} \to \mathbb{N} \setminus \{0\}$ mit r(0)=1 und r(n)=n für $n\neq 0$ ist eine Retraktion, das Bild ist jedoch nicht abgeschlossen.

Deformationsretrakt

heißt Deformationsretrakt von , wenn $i\circ r$ homotop zu $\operatorname{id}_X$ relativ ist.

Deformationsretraktionen sind spezielle Homotopieäquivalenzen, die diese Äquivalenzrelation erzeugen.

Beispiele

Elementares Beispiel

Die folgende Abbildung ist ein anschauliches Beispiel für eine Retraktion in den reellen Zahlen:

$f\colon \mathbb{R} \to [0,1],x\mapsto {\begin{cases}0&{\mbox{für }}x<0\\x&{\mbox{für }}0\leq x\leq 1\\1&{\mbox{für }}x>1\end{cases}}$

Fixpunktsatz von Brouwer im eindimensionalen Fall

Der Fixpunktsatz von Brouwer besagt, dass jede stetige Abbildung einer Vollkugel in sich selbst einen Fixpunkt besitzt. Eine eindimensionale Vollkugel entspricht topologisch gesehen gerade einem abgeschlossenen Intervall, etwa $\left[-1,1\right]$ . Gäbe es nun eine stetige, fixpunktfreie Abbildung $f\colon \left[-1,1\right]\to \left[-1,1\right]$ , so ergäbe sich dadurch eine Retraktion $g\colon \left[-1,1\right]\to \{-1,1\}$ mittels $g(x)=\operatorname{sgn}(x-f(x))=\textstyle {\frac {x-f(x)}{\left|x-f(x)\right|}}$ (da der Nenner nie verschwinden würde), d.h. $\left\{-1,1\right\}$ müsste Retrakt von $\left[-1,1\right]$ sein. Eine solche Retraktion kann aber nicht existieren, da Zusammenhang unter stetigen Abbildungen erhalten ist.

Abgeschlossene Teilräume des Baire-Raums

→ Hauptartikel: Baire-Raum (speziell)

Im Baire-Raum $\mathcal{N}$ gilt: Für jedwede abgeschlossene Teilräume (dies sind stets polnische Teilräume) $X\subset Y\subset {\mathcal {N}}$ ist Retrakt von . Man beachte, dass der Baire-Raum total unzusammenhängend ist, und daher der Zusammenhangsbegriff keinerlei Einschränkungen für Retrakte liefert.

Pfeilkategorie

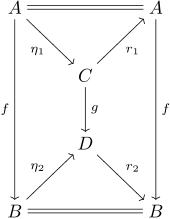
Sei ${\mathcal {C}}$ eine Kategorie, die zugehörige Pfeilkategorie ist dann die Kategorie der Funktoren von der Kategorie mit zwei Objekten und drei Morphismen in die Kategorie ${\mathcal {C}}$ . Diese werden Pfeile genannt und können mit den Morphismen in ${\mathcal {C}}$ identifiziert werden. Ein Pfeil ist Retrakt eines Pfeils , wenn es eine natürliche Transformation (d.h. ein kommutierendes Quadrat) $\eta \colon f\to g$ und eine Retraktion $r\colon g\to f$ gibt, also das folgende Diagramm kommutiert:

Mengenlehre

In der Kategorie ${\mathbf {Set}}$ aller Mengen und den Funktionen zwischen ihnen ist ein Morphismus (das heißt eine Funktion zwischen zwei Mengen) genau dann eine Retraktion, wenn er surjektiv ist. Diese Aussage ist äquivalent zum Auswahlaxiom der Mengenlehre. Entsprechend ist ein Morphismus genau dann eine Koretraktion, wenn er injektiv ist und es einen Morphismus in der Gegenrichtung gibt. Diese Aussage benötigt jedoch nicht das Auswahlaxiom. Aus diesen Aussagen folgt, dass in jeder konkreten Kategorie die Retraktionen surjektiv und die Koretraktionen injektiv sein müssen, was für allgemeine Epi- bzw. Monomorphismen, welche in der Kategorie der Mengen mit den Retraktionen bzw. Koretraktionen übereinstimmen, im Allgemeinen nicht gilt.

Basierend auf einem Artikel in:

Wikipedia.de