Approximation der Eins

Eine Approximation der Eins ist ein Begriff aus der mathematischen Theorie der Banachalgebren. Viele für Anwendungen wichtige Banachalgebren haben kein Einselement. Eine Adjunktion eines Einselement wäre in der Regel ein unnatürliches Vorgehen. In solchen Situationen können aber die hier zu besprechenden Approximationen der Eins vorliegen, diese bilden dann einen Ersatz für das fehlende Einselement.

Nach Beispielen für Banachalgebren ohne Einselement werden Approximationen der Eins definiert. Schließlich werden für die genannten Beispiele Approximationen der Eins angegeben.

Beispiele für Banachalgebren ohne Einselement

Sei ein lokalkompakter Hausdorffraum. Die C*-Algebra $C_{0}(X)$ der stetigen Funktionen $f:X\rightarrow \mathbb {C}$ , die im Unendlichen verschwinden, hat nur dann ein Einselement, wenn kompakt ist. In diesem Fall ist die konstante Funktion 1 das Einselement. Die C*-Algebra $C_{0}(\mathbb {R} )$ hat kein Einselement.
Sei eine lokalkompakte Gruppe. Dann hat die Faltungsalgebra L¹(G) genau dann ein Einselement, wenn diskret ist. In diesem Fall ist $\delta _{e}:G\rightarrow \mathbb {C} ,\,\delta _{e}(e)=1,\delta _{e}(g)=0$ für alle $g\not =e$ , das Einselement (wobei das neutrale Element der Gruppe ist). Die im Rahmen der Fourier-Transformation untersuchte Algebra $L^{1}(\mathbb{R} )$ hat kein Einselement.
Die C*-Algebra der kompakten Operatoren, die Spurklasse und die Hilbert-Schmidt-Klasse über einem Hilbertraum haben genau dann ein Einselement, wenn die Dimension von endlich ist. In diesem Fall ist die identische Abbildung $1_{H}$ das Einselement. In den für Anwendungen wichtigen Fällen $H=\ell ^{2}$ oder $H=L^{2}(\mathbb {R} )$ liegen keine Einselemente vor.
Die Folgenräume $\ell ^{p},\,1\leq p<\infty$ , sind mit der komponentenweise Multiplikation Banachalgebren ohne Einselement.

Definitionen

Eine links-Approximation der Eins (bzw. rechts-Approximation der Eins) einer Banachalgebra ist ein Netz $(e_i)_{i\in I}$ mit $e_{i}a{\stackrel {i\in I}{\longrightarrow }}a$ (bzw. $ae_{i}{\stackrel {i\in I}{\longrightarrow }}a$ ) für alle $a\in A$ .

Eine (beidseitige) Approximation der Eins ist ein Netz, das gleichzeitig links- und rechts-Approximation der Eins ist.

Eigenschaften des Netzes, wie z.B. Abzählbarkeit oder Beschränktheit, werden auch den Approximationen der Eins zugeschrieben.

Hat ein Einselement , so ist das einelementige Netz (e) eine Approximation der Eins. Banachalgebren mit Approximation der Eins verallgemeinern also Banachalgebren mit Einselement.

Beschränkte Approximationen der Eins

Hat eine beschränkte links-Approximation der Eins $(e_i)_{i\in I}$ und eine beschränkte rechts-Approximation der Eins $(f_{j})_{j\in J}$ , so kann man durch eine einfache Rechnung zeigen, dass $(e_{i}+f_{j}-f_{j}e_{i})_{(i,j)\in I\times J}$ eine beidseitige beschränkte Approximation der Eins ist.

Ist ein Banach--Linksmodul, und hat eine beschränkte Approximation der Eins (e_i)_i mit $e_{i}x\rightarrow x$ für alle $x\in X$ , so kann man jedes $x\in X$ über faktorisieren, das heißt, es gibt ein $a\in A$ und ein $y\in X$ mit $x=ay$ , in Formeln $X=A\cdot X$ .

Der Spezialfall $X=A$ verdient besondere Erwähnung: Ist eine Banachalgebra mit beschränkter Approximation der Eins, so gilt $A=A\cdot A$ , genauer: jedes Element aus lässt sich als Produkt zweier Elemente schreiben.

Beispiele

Nullmultiplikation

Ein von 0 verschiedener Banachraum wird zu einer Banachalgebra, wenn man das Produkt von je zwei Elementen als 0 erklärt. Eine solche Banachalgebra kann keine Approximation der Eins enthalten.

C*-Algebren

Jede C*-Algebra hat eine durch 1 beschränkte Approximation der Eins.

Mit Hilfe des stetigen Funktionalkalküls kann man zeigen, dass $\{x\in A;\,0\leq x,\|x\|\leq 1\}$ bezüglich der Ordnung $\leq$ (siehe Positiver Operator) auf der Menge der selbstadjungierten Elemente eine nach oben gerichtete Menge ist und daher selbst ein Netz darstellt. Dieses Netz ist eine Approximation der Eins.

In vielen Fällen kann man aber einfachere Netze (im separablen Fall sogar Folgen) angeben. Im oben genannten Beispiel $C_{0}(\mathbb {R} )$ sei

Die Folge der Funktionen $e_{n}\,$ bildet eine Approximation der Eins für $C_{0}(\mathbb {R} )$ .

$e_{n}(x)={\begin{cases}1&{\mbox{wenn }}-n\leq x\leq n\\n+1+x,&{\mbox{wenn }}-(n+1)\leq x<-n\\n+1-x,&{\mbox{wenn }}n<x\leq n+1\\0,&{\mbox{sonst}}\end{cases}}$ .

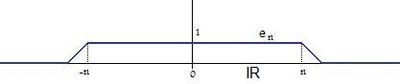
Dann ist die Folge $(e_{n})_{n}$ eine Approximation der Eins in $C_{0}(\mathbb {R} )$ .

Gruppenalgebren

Die Folge der Funktionen $\phi _{n}\,$ bildet eine Approximation der Eins für $L^{1}(\mathbb{R} )$ .

Ist eine lokalkompakte Gruppe, so hat eine durch 1 beschränkte Approximation der Eins.

Sei $\mu$ ein Links-Haarmaß auf . Ist ${{\mathcal U}}$ eine Umgebungsbasis des neutralen Elements von , so gibt es zu jedem $U\in {\mathcal U}$ eine stetige Funktion $\phi _{U}:G\rightarrow \mathbb {R} _{0}^{+}$ mit kompaktem, in gelegenen Träger, $\phi _{U}(t)\,=\,\phi _{U}(t^{-1})$ für alle $t\in G$ und $\int _{G}\phi _{U}(t)\,{\rm {d}}\mu (t)=1$ . Da ${{\mathcal U}}$ als Umgebungsbasis durch die Inklusion gerichtet ist, ist $(\phi _{U})_{U\in {\mathcal {U}}}$ ein Netz, von dem man zeigen kann, dass es eine Approximation der Eins für L^1(G) ist.

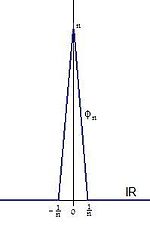
Im Spezialfall $G=\mathbb{R}$ mit dem Lebesgue-Maß als Haar-Maß kann man als Umgebungsbasis die Folge der Mengen $U_{n}=[-{\frac {1}{n}},{\frac {1}{n}}]$ nehmen. Setzt man $\phi _{n}=\phi _{U_{n}}$ wie folgt

$\phi _{n}(x)={\begin{cases}n+n^{2}x&{\mbox{wenn }}-1/n\leq x<0\\n-n^{2}x,&{\mbox{wenn }}0\leq x<1/n\\0,&{\mbox{sonst}}\end{cases}}$

so ist die Folge $(\phi _{n})_{n}$ eine Approximation der Eins für $L^{1}(\mathbb{R} )$ . Man kann auch beliebig oft differenzierbare Funktionen $\phi _{n}$ finden, die eine Approximation der Eins bilden, das spielt eine Rolle in der Theorie der Fourier-Transformation und der Distributionentheorie (Approximation der Delta-Distribution).

Operatorenalgebren

Es sei ${\mathcal E}$ die gerichtete Menge der endlichdimensionalen Teilräume eines unendlichdimensionalen Hilbertraums , $P_{E}$ sei die Orthogonalprojektion auf . Dann ist $(P_{E})_{E\in {\mathcal {E}}}$ eine Approximation der Eins für die C*-Algebra $C(H)$ der kompakten Operatoren auf , sogar eine beschränkte Approximation der Eins, denn Orthogonalprojektionen haben die Operatornorm 1.

Dieses Netz ist auch eine Approximation der Eins in den Schatten-Klassen ${\mathcal S}_p(H)$ , insbesondere also in der Spurklasse und in der Hilbert-Schmidt-Klasse, allerdings nicht beschränkt, denn für die Spurnorm gilt $\|P_{E}\|_{1}={\mbox{dim}}(E)$ , für die Hilbert-Schmidt-Norm gilt $\|P_{E}\|_{2}={\sqrt {{\mbox{dim}}(E)}}$ , allgemein gilt für die Norm der Schattenklasse $\|P_{E}\|_{p}=({\mbox{dim}}(E))^{1/p}$ . Man kann zeigen, dass es in den Schatten-Klassen keine beschränkten Approximationen der Eins gibt. Für die Hilbert-Schmidt-Klasse folgt das aus dem oben genannten Satz über Banach-Linksmoduln, denn ${\mathcal {S}}_{2}(H)\cdot {\mathcal {S}}_{2}(H)={\mathcal {S}}_{1}(H)\not ={\mathcal {S}}_{2}(H)$ .

Basierend auf einem Artikel in:

Wikipedia.de