Äquivariante Abbildung

Unter einer äquivarianten Abbildung versteht man in der Mathematik eine Abbildung, die mit der Wirkung einer Gruppe kommutiert.

Definition

Es seien eine Gruppe und X,Y Mengen, auf denen eine Linksoperation von

$G\times X\to X,\quad (g,x)\mapsto g\cdot x$

definiert ist. Eine Funktion $f\colon X\to Y$ heißt -äquivariant, -Abbildung oder auch kurz äquivariant, wenn gilt:

$f(g\cdot x)=g\cdot f(x)$ für alle $g\in G,x\in X$ .

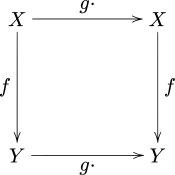
Das bedeutet, dass für jedes $g\in G$ das Diagramm

kommutiert.

Eine äquivalente Definition lautet: Die Gruppe operiere auf der Menge der Abbildungen $X\to Y$ via

$f\mapsto (x\mapsto gf(g^{{-1}}x))$ .

Dann ist eine Abbildung $f\colon X\to Y$ genau dann -äquivariant, wenn sie unter dieser Operation fest bleibt.

ρ-Äquivarianz

Häufig wird in der Mathematik auch der Begriff $\rho$ -Äquivarianz für eine Darstellung

$\rho \colon G\to \mathrm {GL} (V)$

oder allgemeiner für eine Wirkung

$\rho \colon G\to \mathrm {Aut} (Y)$

verwendet. In diesem Kontext heißt eine Abbildung $f\colon X\to Y$ einer G-Menge nach $\rho$ -äquivariant genau dann, wenn

$f(g\cdot x)=\rho (g)\cdot f(x)$ für alle $g\in G,x\in X$ gilt.

Darstellungstheorie und Schurs Lemma

Seien und Vektorräume über einem Körper und sei die Wirkung von auf und linear, d.h. es gebe Darstellungen

$\rho \colon G\rightarrow \mathrm {GL} (X),\tau \colon G\rightarrow \mathrm {GL} (Y)$

mit

$g\cdot x=\rho (g)x,g\cdot y=\tau (g)y$

für alle $x\in X,y\in Y,g\in G$ .

Äquivariante Abbildungen sind dann also Abbildungen mit

$f(\rho (g)x)=\tau (g)(f(x))$

fūr alle und . Äquivariante Abbildungen werden im Kontext der Darstellungstheorie auch Vertauschungsoperatoren (englisch intertwining operator) genannt.

Äquivariante Abbildungen zwischen irreduziblen Darstellungen beschreibt das Lemma von Schur:

Wenn $\rho \colon G\to \mathrm {GL} (V)$ und $\tau \colon G\to \mathrm {GL} (W)$ zwei irreduzible Darstellungen sind, dann ist jede G-äquivariante Abbildung $f\colon V\rightarrow W$ entweder 0 oder ein Isomorphismus.

Falls ein endlichdimensionaler Vektorraum über einem algebraisch abgeschlossenen Körper , z.B. den komplexen Zahlen $\mathbb {C}$ , ist und $\rho \colon G\to \mathrm {GL} (V)$ und $\tau \colon G\to \mathrm {GL} (V)$ wieder irreduzible Darstellungen sind, dann ist jede G-äquivariante Abbildung $f\colon V\rightarrow V$ die Multiplikation mit einem Skalar: es gibt $\lambda \in K$ , so dass für alle $v\in V$ gilt:

$f(v)=\lambda v$ .

Analog gilt für Hilbertraum-Darstellungen topologischer Gruppen, wie sie in der harmonischen Analyse betrachtet werden, das heißt stetige Homomorphismen einer topologischen Gruppe in die unitäre Gruppe auf einem möglicherweise unendlichdimensionalen Hilbertraum versehen mit der schwachen Operatortopologie, dass jeder stetige lineare (eine Verallgemeinerung auf abgeschlossene dicht definierte ist möglich) Vertauschungsoperator (äquivariante Abbildung) zwischen zwei irreduziblen Darstellungen Vielfaches einer Isometrie ist. Die (stetigen) Vertauschungsoperatoren zwischen einer unitären Darstellung und sich selbst bilden eine Von-Neumann-Algebra.

Gruppenalgebren

Darstellungen $\rho \colon G\to \mathrm {GL} (V)$ einer Gruppe auf einem -Vektorraum kann man linear fortsetzen zu einer Darstellung $\rho \colon K(G)\to \mathrm {GL} (V)$ der Gruppenalgebra K(G) , damit wird zu einem K(G) -Modul. Wenn nun $\rho \colon G\to \mathrm {GL} (V),\tau \colon G\to \mathrm {GL} (W)$ zwei Darstellungen sind, die wir in diesem Sinne als K(G) -Moduln auffassen, dann ist eine Abbildung $f\colon V\to W$ -äquivariant genau dann wenn sie K(G) -linear ist.

Selbiges gilt für Darstellungen beliebiger Algebren (siehe auch hier).

Die -äquivarianten Abbildungen zwischen zwei Darstellungen bilden einen Vektorraum.

Für eine feste Gruppe und einen festen Körper bilden die -Darstellungen von und die -äquivarianten Abbildungen die Objekte und Morphismen einer angereicherten Kategorie über der Kategorie der -Vektorräume versehen mit dem üblichen Tensorprodukt. Dabei ist

$\mathrm {id} _{V}\colon K\to \mathrm {Hom} (V,V)$ gegeben durch $(\mathrm {id} _{V}(k))(v)=kv$ und

$\cdot _{UVW}\colon \mathrm {Hom} (V,W)\otimes \mathrm {Hom} (U,V)\to \mathrm {Hom} (U,W)$ ist gegeben durch $\cdot _{{UVW}}(f\otimes g)=fg$ .

Topologie

Ein G-Raum ist ein topologischer Raum X mit einer stetigen Wirkung der Gruppe G. Eine G-Abbildung ist eine äquivariante stetige Abbildung $f:X\rightarrow Y$ zwischen zwei G-Räumen.

Beispiel: G=SO(2) wirke auf $X=Y={\mathbb R}^{2}$ durch Drehungen um den Nullpunkt. Die durch

gegebene Spiegelung $f:{\mathbb R}^{2}\to {\mathbb R}^{2}$ ist SO(2) -äquivariant.

Zwei G-Abbildungen $f_{0},f_{1}\colon X\rightarrow Y$ heißen G-homotop, wenn es eine G-Abbildung

$H\colon X\times \left[0,1\right]\rightarrow Y$

mit

$H(x,0)=f_{0}(x),H(x,1)=f_{1}(x)$

für alle $x\in X$ gibt. (Hierbei wirkt G auf $X\times \left[0,1\right]$ durch $g\cdot (x,t)=(g\cdot x,t)$ .) Die Menge der G-Homotopieklassen von G-Abbildungen $f:X\rightarrow Y$ wird mit $\left[X,Y\right]_{G}$ bezeichnet.

Die äquivarianten Homotopiegruppen eines G-Raumes X sind definiert durch

$\pi _{n}^{G}(X):=\left[S^{n},X\right]_{G}$ .

Man hat einen Isomorphismus $\pi _{n}^{G}(X,x)\cong \pi _{n}(X^{G})$ , wobei $X^{G}=\left\{x\in X:g\cdot x=x\forall g\in G\right\}$ die Menge der Fixpunkte der G-Wirkung ist.

Die äquivarianten Homologiegruppen eines G-Raumes X sind definiert durch

$H_{n}^{G}(X;\mathbb{Z } ):=H_{*}(X\times _{G}EG;\mathbb{Z } )$ ,

wobei EG ein schwach kontrahierbarer topologischer Raum mit einer freien G-Wirkung ist. Wenn die G-Wirkung auf X ebenfalls frei ist, dann ist $H_{n}^{G}(X;\mathbb{Z } )\cong H_{n}(X/G;\mathbb{Z } )$ .

Die äquivariante K-Theorie $K_{G}(X)$ eines kompakten G-Raumes X ist definiert als der Quotient der freien abelschen Gruppe auf den Isomorphieklassen von komplexen G-Vektorbündeln über X nach der von Elementen der Form $[E\oplus F]-[E]-[F]$ erzeugten Untergruppe. Zum Beispiel ist $K_{G}(Punkt)=R(G)$ der komplexe Darstellungsring der Gruppe .

Verallgemeinerungen

Allgemeiner betrachtet man Gruppenoperationen auf Objekten beliebiger Kategorien, dies sind dann Homomorphismen von einer Gruppe in die Automorphismengruppe eines Objekts. Entsprechend betrachtet man auch Halbgruppenoperationen (dies schließt etwa Algebrendarstellungen mit ein) als Homomorphismen in die Endomorphismenhalbgruppe eines Objekts. Von einer -äquivarianten Abbildung wird dann gefordert, ein Morphismus zwischen den beiden Objekten, auf denen die Gruppe wirkt, zu sein. Da es sich dabei nicht mehr notwendigerweise um Abbildungen handelt, spricht man im allgemeinen Fall auch von (-)äquivarianten Morphismen.

Auf der anderen Seite kann eine Gruppe als spezieller Monoid und mithin als spezielle Kategorie ${\mathcal {C}}$ mit einem einzigen Objekt betrachtet werden. Ein Funktor $F\colon {\mathcal C}\to {\mathbf {Set}}$ ist dann die Entsprechung einer -Linksoperation auf F(*) und natürliche Transformationen zwischen solchen Funktoren entsprechen äquivarianten Abbildungen.

Basierend auf einem Artikel in:

Wikipedia.de