Vektorbündel

Vektorbündel oder manchmal auch Vektorraumbündel sind Familien von Vektorräumen, die durch die Punkte eines topologischen Raumes parametrisiert sind. Vektorbündel gehören damit auch zu den Faserbündeln. Existiert zu jedem Vektorraum des Vektorbündels eine Menge von Basen, so kann auch diese Menge ein Faserbündel bilden. Man spricht dann von Rahmen- oder auch Reperbündeln. Diese speziellen Faserbündel sind zugleich auch Hauptfaserbündel.
Anschaulich besteht ein Vektorbündel aus je einem Vektorraum für jeden Punkt des Basisraumes. Da Vektorräume gleicher Dimension jedoch stets isomorph sind, liegt die wesentliche Information in den Beziehungen zwischen diesen Vektorräumen. Das bekannteste Beispiel für ein Vektorbündel ist das Tangentialbündel einer differenzierbaren Mannigfaltigkeit. Der Zusammenhang zwischen den verschiedenen Tangentialräumen, also den Vektorräumen zu den einzelnen Punkten, äußert sich beispielsweise in der Frage, ob ein Vektorfeld differenzierbar ist.
Die Frage, wie Vektorbündel auf einem Raum aussehen können, hängt eng mit globalen topologischen Eigenschaften des Raumes zusammen. Nicht-isomorphe Vektorbündel können oft durch ihre charakteristischen Klassen unterschieden werden.
Definitionen
Vektorbündel
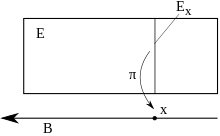
Sei
ein reeller beziehungsweise komplexer n-dimensionaler Vektorraum. Ein reelles
beziehungsweise komplexes Vektorbündel vom Rang
ist ein Tripel
,
bestehend aus topologischen
Räumen
(Totalraum) und
(Basis) sowie einer stetigen surjektiven Abbildung
,
so dass gilt:
- Für jeden Punkt
von
trägt die Faser
von
über
die Struktur eines reellen beziehungsweise komplexen n-dimensionalen Vektorraums.
- „Lokale Trivialität“: Zu jedem Punkt
existiert eine Umgebung
von
und ein Homöomorphismus
-
,
- der mit
kompatibel ist, das heißt
, und für den
- für jedes
in
ein Isomorphismus von Vektorräumen ist. Dabei bezeichnet
die Projektion auf den ersten Faktor. Ein solches
heißt lokale Trivialisierung.
Ein Vektorbündel
heißt trivial, wenn es eine Trivialisierung mit
gibt.
ist ein triviales Vektorbündel.
In verkürzter Ausdrucksweise spricht man oft vom „Vektorbündel “,
womit das Tripel
implizit benannt wird.
Geradenbündel
Ein Vektorbündel mit Rang 1 wird Geradenbündel (als Fehlübersetzung aus dem Englischen auch Linienbündel) genannt.
Beispiele
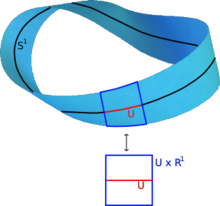
- Das Tangentialbündel einer differenzierbaren Mannigfaltigkeit ist ein Vektorbündel bestehend aus den Tangentialräumen der Mannigfaltigkeit. Entsprechend ist auch das Kotangentialbündel bestehend aus den Kotangentialräumen – also den Dualräumen der Tangentialräume – ein Vektorbündel.
- Das Möbiusband
ist ein Geradenbündel über der 1-Sphäre
(Kreis)
. Lokal ist es homöomorph zu
, wobei
eine offene Teilmenge von
ist. Allerdings ist das Möbiusband nicht homöomorph zu
, was ein Zylinder wäre.
- Der Raum der Differentialformen ist als Bündel der äußeren Algebra auch ein Vektorbündel.
- Das
-Tensorbündel ist ebenfalls ein Vektorbündel, das die zuvor gelisteten Vektorbündel als Spezialfälle umfasst.
Homomorphismus von Vektorbündeln
Homomorphismus
Ein Vektorbündelhomomorphismus von dem Vektorbündel
in das Vektorbündel
ist ein Paar
von stetigen
Abbildungen
und
,
so dass
gilt und
für alle
eine lineare Abbildung ist.
Oftmals wird ein Vektorbündelhomomorphismus kurz als Bündelhomomorphismus oder als Homomorphismus bezeichnet.
Isomorphismus
Ein Vektorbündelhomomorphismus
von
nach
ist ein Vektorbündelisomorphismus, falls
und
Homöomorphismen
sind und die induzierte lineare Abbildung
ein Vektorraumisomorphismus
ist.
Beispiel
Betrachtet man den Kreis
als Mannigfaltigkeit, dann ist das Tangentialbündel
vom
isomorph zu dem trivialen Vektorbündel
.
Der Homöomorphismus zwischen den Basisräumen ist die identische
Abbildung und der zwischen den Totalräumen lautet
für
und
.
Unterstrukturen
Untervektorbündel
Mit
werden die Fasern des Vektorbündels
am Punkt
bezeichnet. Ein Untervektorbündel des Vektorbündels
besteht aus einem topologischen Teilraum
bestehend aus einer Familie von Untervektorräumen
von
,
so dass
ein eigenes Vektorbündel ist.
Eingeschränktes Vektorbündel
Mit
werden wieder die Fasern des Vektorbündels
am Punkt
bezeichnet und
bezeichnet einen topologischen Teilraum. Das auf
eingeschränkte Vektorbündel
ist definiert durch
.
Das eingeschränkte Vektorbündel ist ein eigenständiges Vektorbündel bezüglich
des topologischen Teilraums .
Konstruktionen mit Vektorbündeln
Zurückgezogenes Vektorbündel
Für ein Vektorbündel
und eine stetige Abbildung
definiert man das zurückgezogene Vektorbündel (engl.: "pull-back" oder "induced
bundle", siehe auch Rücktransport)
als das Bündel über
mit Totalraum
und Projektion .
Die Vektorraum-Struktur wird definiert durch
.
Man kann zeigen, dass dies wieder ein lokal triviales Vektorbündel definiert.
Für die durch
definierte Abbildung
gilt also
und für jedes
induziert
einen Vektorraum-Isomorphismus
.
Für jede Bündelabbildung
hat man einen Isomorphismus
,
wobei
die zu
gehörende Abbildung der Basen ist.
Direktes Produkt, Whitney-Summe, Tensorprodukt
Für zwei Vektorbündel
definiert man das direkte Produkt als
wobei jede Faser
mit der Vektorraum-Struktur als direkte
Summe der Vektorräume
und
versehen wird.
Seien jetzt
Vektorbündel über derselben Basis, also
.
Ihre Whitney-Summe wird dann mit Hilfe der Diagonal-Abbildung
definiert als zurückgezogenes Bündel
.
Die Whitney-Summe ist also gerade das Vektorbündel über ,
dessen Faser über
die direkte Summe
ist.
Analog wird das Tensorprodukt
definiert als das Vektorbündel, dessen Faser über
das Tensorprodukt
ist.
Weitere Objekte bei Vektorbündeln
Schnitt
Ist
eine offene Teilmenge von
,
so heißt eine Abbildung
für die
gilt, ein Schnitt von
über
.
Die Menge
aller Schnitte von
über
bildet einen Vektorraum.
Rahmen
Unter einem Rahmen (englisch frame, französisch repère) versteht man eine Art Basis eines Vektorbündels. Es handelt sich um n linear unabhängige Vektoren zu jeder Faser. Diese Vektoren bilden also an jedem Punkt eine Basis der Faser. Präzise bedeutet dies:
Sei
und sei
eine offene Teilmenge des Basisraums. Ein lokales Reper oder Rahmen von
über
ist ein geordnetes n-Tupel
.
Dabei ist für alle i
ein Schnitt
in
über
,
so dass
eine Basis der Faser
für alle
bildet. Falls man
wählen kann, so spricht man von einem globalen Rahmen.
Vektorbündel mit zusätzlichen Strukturen
Differenzierbares Vektorbündel
Sei
ein Vektorbündel. Sind
und
differenzierbare
Mannigfaltigkeiten und sind die Projektion
sowie die Trivialisierungen
differenzierbar, so heißt das Vektorbündel differenzierbar. Es heißt
glatt, wenn die Mannigfaltigkeiten
glatt sind und die Abbildungen beliebig oft differenzierbar sind.
Holomorphes Vektorbündel
Ein holomorphes Vektorbündel ist ein komplexes Vektorbündel
über einer komplexen
Mannigfaltigkeit
,
so dass der Totalraum
eine komplexe Mannigfaltigkeit und die Projektion
eine holomorphe
Abbildung ist.
G-Vektorbündel
Sei
eine Gruppe. Wenn
und
G-Räume sind,
dann ist ein Vektorbündel
ein G-Vektorbündel falls die Gruppenwirkung
für alle
eine lineare Abbildung ist.
Klassifizierender Raum und klassifizierende Abbildung
Der klassifizierende Raum für -dimensionale
reelle Vektorbündel ist die
Graßmann-Mannigfaltigkeit
der
-dimensionalen
Unterräume im
,
diese wird als
bezeichnet. Das bedeutet: jedes
-dimensionale
reelle Vektorbündel
ist von der Form
für eine stetige Abbildung
(die sogenannte klassifizierende Abbildung des Bündels) und das
tautologische
Bündel
,
und zwei Bündel sind isomorph genau dann, wenn ihre klassifizierenden
Abbildungen homotop
sind.
Analog ist ,
die Graßmann-Mannigfaltigkeit der
-dimensionalen
Unterräume im
,
der klassifizierende Raum für
-dimensionale
komplexe Vektorbündel.
Stabile Vektorbündel
Zwei Vektorbündel
und
heißen stabil äquivalent, wenn es triviale Vektorbündel
(nicht notwendig derselben Dimension) mit
gibt. Die Äquivalenzklassen dieser Äquivalenzrelation werden als stabile Vektorbündel bezeichnet. (Diese Definition steht in keinem Zusammenhang mit dem Begriff der stabilen Vektorbündel in der Algebraischen Geometrie.)
Es seien
und
die aufsteigenden Vereinigungen (d.h. die Kolimiten bzgl. der mittels
definierten Inklusionen
und
),
dann kann man zu einem Vektorbündel
und seiner klassifizierenden Abbildung
bzw.
die Komposition mit der Inklusion
bzw.
betrachten. Zwei Vektorbündel sind genau dann stabil äquivalent, wenn die
entsprechenden Abbildungen
bzw.
homotop sind.
Vektorbündel in der algebraischen Geometrie
Definition
Für (algebraische) Vektorbündel in der algebraischen
Geometrie sind
und
Schemata,
ist für alle Punkte
von
ein
-Vektorraum,
und die lokalen Trivialisierungen sind Isomorphismen
Meist ist mit „Vektorbündel“ in der algebraischen Geometrie jedoch eine lokal freie Garbe gemeint (s.u.).
Lokalfreie Garbe
Es sei
ein lokal geringter Raum, z.B. ein topologischer Raum mit der Garbe der stetigen
reell- oder komplexwertigen Funktionen, eine differenzierbare Mannigfaltigkeit
mit der Garbe der
-Funktionen
oder ein Schema.
Eine lokal freie Garbe ist ein -Modul
,
der lokal isomorph zu einem freien
-Modul
ist, d.h.
kann durch offene Mengen
überdeckt werden, für die
isomorph zu einer direkten Summe von Kopien von
ist.
Lokalfreie Garben und Vektorbündel
Die beiden folgenden Konstruktionen liefern im Fall von topologischen Räumen
oder differenzierbaren Mannigfaltigkeiten eine Äquivalenz der Kategorien von lokal
freien Garben sowie Vektorbündeln auf
(der Einfachheit der Notation halber ist der Fall von reellen Vektorbündeln über
einem topologischen Raum beschrieben):
- Einem Vektorbündel wird die Garbe seiner Schnitte zugeordnet.
- Einer lokal freien Garbe
wird die disjunkte Vereinigung
ihrer Fasern
zugeordnet. Wir wählen eine offene Überdeckung
von
, so dass
auf jedem
trivial wird. Eine Trivialisierung definiert
nirgends verschwindende Schnitte von
über
, die fasernweise eine Basis bilden. Diese definieren eine Abbildung
-
,
- und wir definieren die Topologie auf
dadurch, dass wir fordern, dass diese Abbildungen Homöomorphismen sind. Sie ist wohldefiniert, da sich diese Abbildungen über dem Schnitt zweier Mengen
und
nur um einen Homöomorphismus (genauer gesagt einen stetig variierenden Vektorraumautomorphismus von
) unterscheiden.
Im Fall der algebraischen Geometrie ist diese Konstruktion etwas einfacher:
das Bündel zu einer lokalfreien Garbe
ist
dabei bezeichnet
die symmetrische
Algebra und
das Algebrenspektrum.
Weiterführende Begriffe
- Die Untersuchung so genannter stabiler Äquivalenzklassen von Vektorbündeln ist Gegenstand der K-Theorie.
- Auf algebraischen Kurven haben (semi-)stabile Vektorbündel besonders gute Eigenschaften.
Literatur
- Karlheinz Knapp: Vektorbündel. Springer Fachmedien, Wiesbaden 2013, ISBN 978-3-658-03113-8.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 09.05. 2021