Spezifische Wärmekapazität

Name

spezifische Wärmekapazität

Größen- und Einheitensystem	Einheit	Dimension
SI	J/(kg·K)	L²·T⁻²·Θ⁻¹

Die spezifische Wärmekapazität, auch spezifische Wärme oder verkürzt Wärmekapazität, ist eine Stoffeigenschaft der Thermodynamik. Sie bemisst die Fähigkeit eines Stoffes, thermische Energie zu speichern.

Definition

Definition der spezifischen Wärmekapazität

Die spezifische Wärmekapazität eines Stoffes in einem bestimmten Zustand ist die Wärme, die einer Menge des Stoffes zugeführt oder entzogen wird, dividiert durch die zugehörige Temperaturerhöhung oder -erniedrigung und die Masse des Stoffes:

$c={\frac {\Delta Q}{m\cdot \Delta T}}$

Dabei ist

$\Delta Q$ die Wärme, die dem Stoff zugeführt oder entzogen wird,
die Masse des Stoffes,
$\Delta T=T_{2}-T_{1}$ die Differenz von End- und Anfangstemperatur.

Die Einheit der spezifischen Wärmekapazität ist im Internationalen Einheitensystem (SI):

$[c]=\mathrm {\frac {J}{kg\cdot K}}$

Beispielsweise beträgt die spezifische Wärmekapazität von flüssigem Wasser $c=4{,}182\,\mathrm {\tfrac {kJ}{kg\cdot K}}$ . Das bedeutet, dass man einem Kilogramm Wasser eine Energie von 4,182 Kilojoule zuführen muss, um es um 1 Kelvin zu erwärmen.

Im Allgemeinen ist die spezifische Wärmekapazität von Zustandsgrößen insbesondere von der Temperatur abhängig. Daher gelten Werte für die spezifische Wärmekapazität nur für eine bestimmte Temperatur, häufig für 25 °C. Messungen der Temperaturabhängigkeit c(T) erfolgen z.B. durch dynamische Leistungs(differenz)kalorimetrie. Historisch haben solche Messungen, insbesondere bei tiefen Temperaturen, die Festkörperphysik wesentlich vorangebracht.

Bei einem Phasenübergang erster Ordnung ist die Wärmekapazität nicht definiert, Messwerte divergieren dort. Ein Sprung in c(T) zeigt dagegen einen Phasenübergang zweiter Ordnung an, bei dem sich die Anzahl von Freiheitsgraden im Material ändert.

Zudem ist die spezifische Wärmekapazität von der Prozessführung der Erwärmung bzw. Abkühlung abhängig, vor allem bei Gasen. Insbesondere wird zwischen der spezifischen Wärme bei konstantem Volumen c_V und der bei konstantem Druck $c_{p}$ unterschieden. Bei konstantem Volumen kommt die gesamte Wärmezufuhr der Temperaturerhöhung zugute. Wenn sich das Gas jedoch ausdehnen kann, dann wird ein Teil der Wärme für die Verrichtung der Expansionsarbeit aufgewendet und fehlt damit für die Temperaturerhöhung.

Mittlere und wahre spezifische Wärmekapazität

Die Formel der Einleitung gibt die mittlere spezifische Wärmekapazität $c\vert _{T_{1}}^{T_{2}}$ für das Temperaturintervall $[T_{1},T_{2}]$ an. Diese lässt sich

für Temperaturbereiche, die zwischen $T_{0}=0\;^{\circ }\mathrm {C}$ und einer beliebigen Temperatur $T_{x}$ liegen, aus Tabellenwerken ablesen oder, falls sie dort nicht aufgeführt ist, aus ihnen durch Interpolation annähern;
für Temperaturbereiche, die nicht bei $T_{0}=0\;^{\circ }\mathrm {C}$ beginnen, wie folgt berechnen:

$c\vert _{T_{1}}^{T_{2}}={\frac {c\vert _{T_{0}}^{T_{2}}\cdot (T_{2}-T_{0})-c\vert _{T_{0}}^{T_{1}}\cdot (T_{1}-T_{0})}{T_{2}-T_{1}}}$

Für genauere Betrachtungen ist zur wahren spezifischen Wärmekapazität bei der Temperatur $T_{1}$ überzugehen, d.h. zum Grenzfall beliebig kleiner Temperaturänderungen:

$c\vert _{T_{1}}=\lim _{T_{2}\rightarrow T_{1}}{\frac {\Delta Q}{m\cdot \Delta T}}$

Werte für ausgewählte Materialien

Feststoffe		Gase (c_p)
Material	c in kJ/(kg·K)	Material	c in kJ/(kg·K)
Eis (0 °C)	02,060	Wasserstoff	14,32
Eis (−10 °C)	02,22	Helium	05,193
Natrium	01,234	Methan	02,158
Magnesium	01,046	Wasserdampf (100 °C)	02,080
Aluminium	00,896	Butan	01,658
Eisen	00,452	Neon	01,030
Kupfer	00,382	Luft (20 °C trocken)	01,005
Silber	00,235	Argon	00,523
Blei	00,129	Baustoffe
Flüssigkeiten		Beton	00,88
Wasser (20 °C)	04,182	Gips, Schamotte	≈1
Ethanol	02,43	Holzfaserdämmstoff, Zelluloseflocken	02,1
Petroleum	02,14	Polystyrol	01,4
Quecksilber	00,139	Mineralfaserdämmstoff	00,8

Beziehungen zu Wärmekapazität und molarer Wärmekapazität

Ändert sich die Temperatur eines Körpers um die Temperaturdifferenz $\Delta T$ , so wird dabei die Wärme

$\Delta Q=C\,\Delta T$

übergeben, vorausgesetzt, die Wärmekapazität des Körpers ist in diesem Temperaturintervall zumindest näherungsweise temperaturunabhängig. Im Gegensatz zur Volumen- oder Masse-bezogenen Wärmekapazität ist die (absolute) Wärmekapazität keine Stoffeigenschaft, sondern die Eigenschaft eines Körpers.

Handelt es sich um einen homogenen Körper, so kann man auch die Masse-spezifische Wärmekapazität angeben:

$\Delta Q=c\,m\,\Delta T$

Bezieht man die Wärmekapazität nicht auf die Masse des Stoffes, sondern auf seine Stoffmenge , so lautet obige Gleichung unter Verwendung der molaren Wärmekapazität $C_{\mathrm {m} }$ (veraltet auch Molwärme genannt):

$\Delta Q=C_{\mathrm {m} }\,n\,\Delta T$

Zwischen der Wärmekapazität , der spezifischen Wärmekapazität und der molaren Wärmekapazität $C_{\mathrm {m} }$ besteht der Zusammenhang

$C=c\,m=C_{\mathrm {m} }\,n$ .

Nach Division durch die Stoffmenge wird daraus

${\frac {C}{n}}=c\,M=C_{\mathrm {m} }$

mit der molaren Masse $M={\tfrac {m}{n}}$ .

Am Beispiel Kupfer ergibt sich: $c={0{,}38\,\mathrm {\tfrac {J}{g\cdot K}} ,\,M=63\,\mathrm {\tfrac {g}{mol}} \,\Rightarrow C_{\mathrm {m} }=c\cdot M=24\,\mathrm {\tfrac {J}{mol\cdot K}} }$

Wärmekapazität idealer Gase

Aus den thermodynamischen Zustandsgleichungen des idealen Gases

thermisch: $p\,V=n\,R\,T$

kalorisch: $U=n\,C_{\mathrm {m} ,V}\,T$

und der Definition der Enthalpie:

$H=n\,C_{\mathrm {m} ,p}\,T=U+p\,V$

folgt für die molaren Wärmekapazitäten bei konstantem Volumen $C_{\mathrm {m} ,V}$ (isochor) und bei konstantem Druck $C_{\mathrm {m} ,p}$ (isobar):

$C_{\mathrm {m} ,p}=C_{\mathrm {m} ,V}+R$

mit der universellen Gaskonstante $R=8{,}314\;\mathrm {\tfrac {J}{mol\;K}}$ .

Gegenüber der molaren Wärmekapazität bei konstantem Volumen fällt diejenige bei konstantem Druck größer aus, weil das Gas in diesem Fall beim Erwärmen expandiert und damit gegen den Außendruck Arbeit leistet. Der entsprechende Anteil der zugeführten Wärme kommt nicht der inneren Energie des Gases und damit auch nicht der Temperaturerhöhung zugute. Deshalb muss für eine bestimmte Temperaturerhöhung mehr Wärme zugeführt werden, der Quotient und damit die molare Wärmekapazität vergrößern sich.

Der Isentropenexponent ist definiert als:

$\kappa ={\frac {C_{\mathrm {m} ,p}}{C_{\mathrm {m} ,V}}}={\frac {c_{m,p}}{c_{m,V}}}={\frac {C_{p}}{C_{V}}}={\frac {c_{p}}{c_{V}}}$

Allgemeiner Fall

In guter Näherung gilt:

mit $\;C_{\mathrm {m} ,V}={\frac {f}{2}}\,R\;$ und $\;C_{\mathrm {m} ,p}={\frac {f+2}{2}}\,R\;$ folgt $\;\kappa ={\frac {f+2}{f}}=1+{\frac {2}{f}}\;$ .

mit der Gesamtzahl $f=f_{\mathrm {trans} }+f_{\mathrm {rot} }+f_{\mathrm {vib} }$ der energetischen Freiheitsgrade eines Moleküls mit den Anteilen

$f_{\mathrm {trans} }=3$ für die translatorische kinetische Energie des Schwerpunkts
$f_{\mathrm {rot} }\in \{0,2,3\}$ für die Rotationsenergie (Erläuterung s.u.)
$f_{\mathrm {vib} }=2\,l$ für die innere Energie der Normalschwingungen der Atomkerne gegeneinander (jede Schwingung bringt einen zusätzlichen Freiheitsgrad für die kinetische Energie und einen für die potentielle Energie).

1-atomiges Gas

Das einfachste Modellsystem betrachtet die Atome als Massepunkte: $N\gg 1$ von ihnen (Teilchenzahl) fliegen in einem Kasten mit Volumen frei umher und üben durch Stöße gegen die Wand einen Druck aus. Im zeitlichen Mittel ergibt sich nach der kinetischen Gastheorie für den Druck auf die Wand die Gleichung:

$p\,V={\frac {2}{3}}\,N\,\langle E_{\mathrm {kin} }\rangle$

Darin ist $\langle E_{\mathrm {kin} }\rangle$ die durchschnittliche kinetische Energie eines Teilchens.

Für die gesamte kinetische Energie $N\,\langle E_{\mathrm {kin} }\rangle$ aller Teilchen ergibt sich durch Vergleich mit der Zustandsgleichung $p\,V=n\,R\,T$ des idealen Gases:

$\Rightarrow N\,\langle E_{\mathrm {kin} }\rangle ={\frac {3}{2}}\,n\,R\,T$

Dieses Ergebnis folgt auch aus dem Gleichverteilungssatz der statistischen Mechanik, nach dem jedes Teilchen in jedem seiner Freiheitsgrade der Bewegung im Durchschnitt die Energie $k_{B}T/2$ besitzt; mit den drei Freiheitsgraden des einatomigen Gases ergibt sich:

$\langle E_{\mathrm {kin} }\rangle ={\frac {3}{2}}\,k_{\mathrm {B} }\,T$

mit

der Boltzmann-Konstante $k_{\mathrm {B} }={\tfrac {R}{N_{\mathrm {A} }}}$
der Avogadro-Konstante $N_{{\mathrm {A}}}={\tfrac {N}{n}}$ .

Der Massepunkt hat $f=f_{\text{trans}}=3$ Freiheitsgrade, entsprechend den drei Raumdimensionen. Zwar kann ein einzelnes Atom auch rotieren in dem Sinn, dass es in seinen angeregten Zuständen höheren Drehimpuls hat als im Grundzustand. Diese Zustände entsprechen elektronischen Anregungen und haben Anregungsenergien, die aufgrund der Kleinheit des Massenträgheitsmoments wegen der Drehimpulsquantelung bei mindestens einigen eV liegen, also weit höher als die typische thermische Energie $k_{\mathrm {B} }\,T$ , sodass im thermischen Gleichgewicht keine Anregung erfolgen kann $\left(f_{\text{rot}}=0\right)$ .

Identifiziert man die thermodynamische innere Energie mit der gesamten kinetischen Energie, so folgt die kalorische Zustandsgleichung des einatomigen idealen Gases:

$U={\frac {3}{2}}\,n\,R\,T$

Folglich ist

$C_{\mathrm {m} ,V}={\frac {3}{2}}\,R\ \Rightarrow \ C_{\mathrm {m} ,p}={\frac {5}{2}}\,R\ \Rightarrow \ \kappa ={\frac {5}{3}}=1{,}666\ldots$

Größerer Temperaturbereich

Diese Werte stimmen mit Messungen an Edelgasen und an Quecksilber dampf hervorragend überein, wenn die Temperatur bzw. der Druck genügend weit über dem Verflüssigungspunkt liegt. Die erste Messung erfolgte im Jahr 1876 an dünnem Quecksilberdampf bei etwa 300 °C. Der über die Schallgeschwindigkeit bestimmte Isentropenexponent $\kappa \approx 1{,}66$ bestätigte erstmals, dass freie Atome sich über einen großen Temperaturbereich wie Massepunkte verhalten.

2-atomiges Gas

Das einfachste Modell für ein zweiatomiges Gas ist eine starre Hantel $\left(l=0\Rightarrow f_{\text{vib}}=0\right)$ . Sie hat $f_{\text{trans}}=3$ Freiheitsgrade für Translationsbewegungen des Schwerpunkts und $f_{\text{rot}}=2$ Freiheitsgrade für Rotationen um die beiden Achsen senkrecht zur Hantelachse; die (im makroskopischen mechanischen Modell gegebene) Möglichkeit der Rotation um die Hantelachse wird nicht mitgezählt, da beide Atomkerne auf der Rotationsachse liegen. Daher besitzen sie – wie beim einatomigen Gas – um diese Achse kein Massenträgheitsmoment und damit auch keine Rotationsenergie.

Mit den o. g. f=3+2=5 Freiheitsgraden folgt aus dem Gleichverteilungssatz:

$U={\frac {5}{2}}\,n\,R\,T$

Folglich ist

$C_{\mathrm {m} ,V}={\frac {5}{2}}\,R\ \Rightarrow \ C_{\mathrm {m} ,p}={\frac {7}{2}}\,R\ \Rightarrow \ \kappa ={\frac {7}{5}}=1{,}4$

Hierzu passen Messwerte für Sauerstoff, Stickstoff, Wasserstoff etc. unter Normalbedingungen hervorragend.

Bei sehr niedrigen Temperaturen

Bei sehr kaltem Wasserstoff $\left(T<200{\text{K}}\right)$ wird eine Abnahme der Molwärme bis auf $C_{\mathrm {m} ,V}={\frac {3}{2}}\,R$ beobachtet, was dem Verhalten eines einzelnen Massepunkts entspricht. Dies wird erklärt durch den quantenphysikalischen Effekt, dass die Rotationsenergie nur diskrete Werte mit bestimmten Abständen annehmen kann (Energiestufen, Quantelung). Bei tiefen Temperaturen kann die Größenordnung der Energien, die typischerweise bei Stößen zwischen den Molekülen ausgetauscht werden (näherungsweise gegeben durch die thermische Energie $E_{\text{th}}=k_{\mathrm {B} }\,T$ ), unter die niedrigste Stufe der Rotationsenergie sinken:

$E_{\text{th}}<E_{\text{rot, min}}$

In diesem Fall können durch die thermischen Stöße keine Rotationen mehr angeregt werden, die Rotationsfreiheitsgrade „frieren ein“, weshalb zweiatomige Gase bei tiefen Temperaturen modellmässig wie einatomige Gase behandelt werden können:

$f_{\text{rot}}=0\Rightarrow f=f_{\text{trans}}=3$

Dieser Effekt ist am deutlichsten ausgeprägt bei Wasserstoff, der bis zu sehr tiefen Temperaturen gasförmig bleibt und dessen Moleküle das kleinste Trägheitsmoment und damit auch die geringste Rotationsenergie haben ( $\kappa ={\frac {5}{3}}\approx 1{,}66$ ).

Bei sehr hohen Temperaturen

Bei höheren bzw. sehr hohen Temperaturen können die Molwärmen steigen bis gegen:

$C_{\mathrm {m} ,V}={\frac {7}{2}}\,R\Rightarrow C_{\mathrm {m} ,p}={\frac {9}{2}}\,R\Rightarrow \kappa ={\frac {9}{7}}\approx 1{,}29$

Das wird erklärt durch das allmähliche „Auftauen“ der Freiheitsgrade für die Schwingung der beiden Atome gegeneinander, d.h., das Modell der starren Hantel gilt bei hohen Temperaturen nicht mehr:

$l=1\Rightarrow f_{\text{vib}}=2\Rightarrow f=3+2+2=7$

3- und mehratomiges Gas

Translations- und Rotationsbewegungen bringen je drei Freiheitsgrade:

$f_{\text{trans}}=f_{\text{rot}}=3,$

sofern nicht alle Kerne auf einer Linie liegen (dann gibt es nur zwei Rotationsfreiheitsgrade, Erläuterung s.o. bei zweiatomigem Gas).

Bei größeren Molekülen sind auch Teile der Schwingsfreiheitsgrade schon bei Normalbedingungen angeregt:

$l\geq 2\Rightarrow f_{\text{vib}}\geq 4\Rightarrow f\geq 10$

Dadurch steigen die Molwärmen höher als bei den 2-atomigen Gasen:

$C_{\mathrm {m} ,V}\geq 5\,R\Rightarrow C_{\mathrm {m} ,p}\geq 6\,R,$

weshalb der Isentropenexponent $\kappa$ weiter fällt:

$\kappa \leq {\frac {6}{5}}=1{,}2$

Wärmekapazität von Festkörpern

Beobachtungen

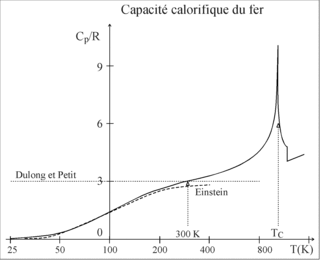
Temperaturverlauf der Wärmekapazität von Eisen (mit Peak bei der Curie-Temperatur)

Die molare Wärme von Festkörpern erreicht nach dem empirisch gefundenen Dulong-Petit-Gesetz bei genügend hohen Temperaturen näherungsweise den gleichen Wert:

$C_{\mathrm {m} }=3\cdot R\approx 25\;\mathrm {\tfrac {J}{mol\cdot K}}$

Zu niedrigen Temperaturen hin nimmt die spezifische Wärme ab, wobei die Form dieser Abhängigkeit für alle Festkörper sehr ähnlich ist, wenn die Temperatur geeignet skaliert wird. Bei sehr tiefer Temperatur nähert die spezifische Wärme sich dem Wert Null, dabei ähnelt der Verlauf für Nichtleiter der Funktion $C_{\mathrm {m} }=f(T^{3})$ , für Metalle der Funktion $C_{\mathrm {m} }=f(T)$ . Bei ferromagnetischen Materialien wie z.B. Eisen liefert die Änderung der Magnetisierung einen Beitrag zur Wärmekapazität.

Modellsystem Massepunkte

Das einfachste Modellsystem des Festkörpers besteht aus $N\gg 1$ Massepunkten, die durch elastische Kräfte an ihre Ruhelage gebunden sind und unabhängig voneinander in jeweils drei Richtungen des Raumes schwingen können. Da jede Schwingung zwei Freiheitsgrade beisteuert, ist die Gesamtzahl der Freiheitsgrade f=6 und die nach dem Gleichverteilungssatz vorhergesagte molare Wärmekapazität

$C_{\mathrm {m} }={\tfrac {6}{2}}R=3R,$

was mit der Regel von Dulong-Petit übereinstimmt.

Einstein-Modell

→ Hauptartikel: Einstein-Modell

Die Abnahme zu tieferen Temperaturen hin zeigt das Einfrieren der Schwingungen. Albert Einstein nahm 1907 an, dass die Schwingungen aller Teilchen dieselbe Frequenz $\nu$ haben und ihre Energie sich nur stufenweise um jeweils $\Delta E=h\cdot \nu$ ändern kann ( ist das Plancksche Wirkungsquantum).

Debye-Modell

Debye-Temperatur ausgewählter Metalle
Metall	Debye- Temperatur
Eisen	0464 K
Aluminium	0426 K
Magnesium	0406 K
Kupfer	0345 K
Zinn	0195 K
Blei	0096 K

→ Hauptartikel: Debye-Modell

Peter Debye verfeinerte das Modell 1912 dahingehend, dass er statt von unabhängigen, individuellen Schwingungen der einzelnen Atome von den elastischen Schwingungen des ganzen Körpers ausging. Bei hoher Temperatur sind sie nach dem Gleichverteilungssatz alle angeregt und ergeben die spezifische Wärme in Übereinstimmung mit dem Wert $C_{\mathrm {m} }=3R$ . Sie haben aber je nach Wellenlänge verschiedene Frequenzen, sodass ihre Energiestufen unterschiedlich weit auseinanderliegen und sich daher der Effekt des Einfrierens über einen weiteren Temperaturbereich verteilt. Nach diesem Debye-Modell wird die molare Wärmekapazität in Abhängigkeit von der Temperatur bestimmt:

$c_{V}(T)=9R\cdot \left({\frac {T}{\Theta _{\mathrm {D} }}}\right)^{3}\cdot \int _{0}^{\frac {\Theta _{D}}{T}}{\frac {x^{4}\cdot \mathrm {e} ^{x}}{\left(\mathrm {e} ^{x}-1\right)^{2}}}\,\mathrm {d} x$

Die Debye-Temperatur $\Theta _{\mathrm {D} }$ als einzige vom Material abhängige Größe gibt den Wert an, mit dem die Temperatur zu skalieren ist, um eine für alle Stoffe einheitliche Kurve zu erhalten: etwa bei der Temperatur $T=0{,}2\cdot \Theta _{\mathrm {D} }$ ist die molare Wärme auf die Hälfte ihres vollen Werts abgefallen.

Das Debye-Modell stimmt bei allen Temperaturen mit den Messungen an Festkörpern sehr gut überein. Es ergibt insbesondere auch in der Nähe des absoluten Nullpunkts richtig das Anwachsen der Wärmekapazität mit $T^{3}$ bei Nichtleitern, während das Einstein-Modell hier ein viel zu schwaches Anwachsen vorhersagt.

Modellsystem Elektronengas

Um die lineare Abhängigkeit der Wärmekapazität von der Temperatur zu verstehen, die die elektrischen Leiter in der Nähe des absoluten Nullpunkts zeigen, kann man die Leitungselektronen als entartes Fermigas auffassen. Mit Hilfe der Fermiverteilung und der Zustandsdichte eines freien Elektrons lässt sich daraus für niedrige Temperaturen die Temperaturabhängigkeit der Gesamtenergie und folglich auch die Wärmekapazität berechnen.

Das Ergebnis stimmt mit den Messwerten überein und ist weit geringer, als wenn man die Leitungselektronen als klassisches einatomiges ideales Gas (wie oben) betrachtete, das sich zusätzlich zu den Atomrümpfen im Festkörper befindet. Die Aufklärung dieser Diskrepanz von ${\tfrac {3}{2}}R$ gilt als ein wesentlicher Fortschritt in der Festkörperphysik der ersten Hälfte des 20. Jahrhunderts.

Basierend auf einem Artikel in Wikipedia.de