
Digitaler Regler
In der Serienfertigung von Regeleinrichtungen werden anstelle der analogen Regler zunehmend digitale Regler eingesetzt, weil sie verschiedene technische Vorteile aufweisen. Dazu gehören: einmaliger Hardware-Entwicklungsaufwand, einfache parametrische System-Änderungen per Software, Realisierung komplexere Reglerstrukturen, Multitasking.
Bei den meisten Regeleinrichtungen handelt es sich bei den Regelstrecken um kontinuierlich wirkende analoge Eingrößensysteme, die sich linear, nichtlinear und totzeitbehaftet verhalten können. Für diese Regelstrecken sollen bestimmte physikalische Größen wie Temperatur, Kraft, Druck, Geschwindigkeit, Niveau usw. geregelt werden. Die dafür erforderlichen Regler können eine analoge oder digitale Systemstruktur aufweisen.
Bei der digitalen Regelung erfolgt im einfachsten Falle eine zeitliche Abtastung und Digitalisierung der Regeldifferenz. Im gleichen Abtast-Intervall berechnet ein Mikrocomputer z.B. mit Hilfe von Differenzengleichungen den notwendigen Regel-Algorithmus. Die digitale Ausgangsgröße des Reglers, die Stellgröße, wird für die meist analog wirkenden Regelstrecken durch Wandler und Speicher analogisiert. Andere Begriffe der digitalen Regelung bezeichnen diesen Vorgang als „zeitdiskrete Regelung“ oder auch als „Abtastregelung“.
Analoge wie digitale Regler benötigen als Eingangssignal die Regelabweichung und einen Regleralgorithmus, der die gewünschte Dynamik des geschlossenen Regelkreises bestimmt.
Digitale Regler werden durch Mikrocomputer realisiert. Der Computer benötigt für die digitale Signalverarbeitung Ein- und Ausgangsschnittstellen, um das kontinuierliche Eingangssignal zyklisch abzutasten und digital mit speziellen Programmiersprachen berechnen zu können. Der Mikrocomputer verarbeitet die abgetasteten Signalwerte als Eingangsfolgen mit Hilfe von Differenzengleichungen zu Ausgangsfolgen. Die so schrittweise errechneten Stellgrößen-Anteile jeder Komponente der Ausgangsfolge werden über einen D/A-Wandler und ein Speicher-Halteglied wieder als feingestuftes quasi kontinuierliches Signal an die kontinuierlich wirkende Regelstrecke geliefert.
Grundlagen der numerischen Berechnung und Regelung
Verhalten der analogen Regler
Das Systemverhalten von kontinuierlich wirkenden linearen, dynamischen Übertragungssystemen wird von gewöhnlichen Differenzialgleichungen mit konstanten Koeffizienten beschrieben. Mittels der Laplace-Transformation können die Terme der Differentialgleichung in den komplexen Bildbereich (s-Bereich) als Übertragungsfunktion mit dem Verhältnis des Ausgangssignals zum Eingangssignal als gebrochen-rationale Gleichung überführt werden:
Mit der Nullstellenbestimmung lassen sich die Polynome der Übertragungsfunktion in die Produktdarstellung mit einzelnen Elementarsystemen erster Ordnung (Linearfaktoren) zerlegen. Diese Form im s-Bereich erlaubt mit der Rücktransformation in den Zeitbereich die Lösung der Differentialgleichung und darüber hinaus Aussagen des Systemverhaltens, der Systemstabilität, der Systemanalyse und der Systemsynthese.
Analoge Standardregler verarbeiten kontinuierliche Signale und bestehen in
der Regel aus Operationsverstärkern mit RC-Spannungsteilern,
die ein rückwirkungsfreies Impedanzverhältnis
bilden. Das zugehörige Systemverhalten im komplexen Frequenzbereich
kann unmittelbar als Verhältnis der Impedanzen als Übertragungsfunktion G(s)
oder G(jω) geschrieben werden.
Bei analogen Reglern stellen die Hardware-Komponenten, z.B. Operationsverstärker mit RC-Beschaltung, die Lösung der Differenzialgleichung des Regelalgorithmus dar.
Verhalten der digitalen Regler
Zeitdiskrete lineare dynamische Systeme sind dadurch gekennzeichnet, dass die inneren Systemzustände nur zu einzelnen Zeitpunkten definiert sind und an den Ein- und Ausgängen zeitdiskrete Signale auftreten. Sie spielen im Rahmen der Informationstechnik und digitalen Signalverarbeitung eine bedeutende Rolle und werden in Form von Zahlenfolgen beschrieben.
- Digitale Ein-Ausgangssignale der Hardware
- Der Rechenalgorithmus eines Digitalrechners erlaubt keine kontinuierliche
Berechnung von analogen zeitabhängigen Signalen. Deshalb werden zu bestimmten
Zeitpunkten die analogen Eingangssignale, z.B. die Regelabweichung
, mit Hilfe eines (idealen)
-Abtasters und einem A/D-Wandlers als
abgetastet. Die Abtastung des kontinuierlichen Signals der Regelabweichung
mit der Abtastfrequenz
erfordert neben dem A/D-Wandler eine funktionell kleine Haltefunktion (Sample-and-Hold-Verfahren), welche dafür sorgen muss, dass der Mikrocomputer den digitalisierten Wert auch sicher erfassen kann.
- Das gewünschte System-Übertragungsverhalten des digitalen Reglers wird für
die gegebene Eingangsfolge mit Differenzengleichungen berechnet und
taktsynchron als Ausgangssignal
mit Zahlenwerten ausgegeben. Ist ein analoges Ausgangssignal erforderlich, erlaubt eine spezielle Hardware mit einem D/A-Wandler mit einer Haltefunktion (Halteglied) die Umwandlung in ein gestuftes quasi-stetiges Ausgangssignal u(t) als Stellgröße des Reglers.
- Mikrocomputer als digitaler Regler
- Bei zeitdiskreten Systemen besteht das Eingangssignal eines dynamischen
Systems im Takt der Abtastung aus nummerierten Folgegliedern
der Eingangsfolge (Wertefolge) und das Ausgangssignal aus Folgegliedern der Ausgangsfolge (Wertefolge). Beim Digitalregler wird diese Folge von Werten der Eingangsfolge mit Differenzengleichungen berechnet zu Folgegliedern der Ausgangsfolge. Die Differenzengleichungen des Digitalreglers bestimmen mit dem Regelalgorithmus und der Stellgröße
in Form von Berechnungspunkten der Ausgangsfolge über die Regelstrecke das dynamische Verhalten des gesamten Regelkreises. Mit der Regelgröße
wird im zeitlichen Abstand der Abtastzeit
eine Annäherung an die gewünschte analytische Funktion
des Regelkreisverhaltens erreicht.
- Da technische Regelstrecken häufig analoge Eingänge aufweisen, muss die Ausgangsfolge des Mikrocomputers über eine geeignete Hardware zu einem quasi analogen Signal umgeformt werden.
- Die Anzahl der Folgeglieder der Abtastung ist nicht begrenzt. Es werden
bei einer Regelung unendlich viele Folgeglieder
im realen zeitlichen Abstand der Abtastzeit
ausgeführt. Benötigt und gespeichert werden aber nur eine aktuelle Programmzeile mit Differenzengleichungen für die Berechnung von Wertefolgen des Stellgliedes
und eine zurückliegende Programmzeile mit den Differenzengleichungen für die Berechnung der Wertefolgen
, sofern es sich um Differenzengleichungen 1. Ordnung handelt. Gespeichert werden also vorübergehend nur die aktuellen Werte der berechneten Differenzengleichungen und die Werte einer zurückliegenden Berechnung der Differenzengleichungen. Weitere zurückliegende Programmzeilen mit Wertefolgen werden nicht benötigt und gelöscht.
- Zum Vergleich: Bei der Simulation eines Regelkreises mit einem
Personalcomputer werden im Abstand
sämtliche Ergebnisse der Differenzengleichungen mit den nummerierten Programmzeilen
als Tabelle mit
-Zeilen abgespeichert. Mit der Simulation wird die Funktion und Sicherheit eines Regelkreises überprüft, weil bei falscher Parametrierung mit Instabilität des Regelkreises die Regelstrecke Schaden annehmen kann.
- Differenzengleichungen
- Für die Aufstellung der meisten Differenzengleichungen werden verschiedene Verfahren eingesetzt, wie das einfache Euler-Streckenzugverfahren oder die besseren und aufwendigeren Mehrschrittverfahren. Die komplizierteren Mehrschrittverfahren benötigen vorteilhaft für ein gleiches genaues Berechnungsergebnis eine wesentlich geringere Anzahl von Folgegleichungen.
- Eine Differenzengleichung ist eine numerisch lösbare Berechnungsvorschrift
für eine diskret
definierte Folge
von Folgegleichungen, welche Variablen
zu fortlaufenden nummerierten Ereignissen bzw. nummerierten Zeitpunkten im Abstand eines Intervalls
berechnen.
- Die rekursive Lösung einer Differenzengleichung erster Ordnung erfolgt von einer Anfangsbedingung durch nummerierte Folgegleichungen, welche sich je auf das Ergebnis einer zurückliegenden Folgegleichung bezieht. Bei Differenzengleichungen höherer Ordnung bezieht sich jede aktuelle Folgegleichung, entsprechend der Ordnungszahl, auf mehrere der zurückliegenden Folgegleichungen.
- Die Allgemeine Form einer rekursiven Differenzengleichung (Euler-Rückwärts) für ein dynamisches System 1. Ordnung lautet:
-
- Dabei ist
ein Wert der Ausgangsgröße,
die vorherige Ausgangsgröße,
die Eingangsgröße,
ein Zeitintervall, „System“ entspricht der Form einer modifizierten Differentialgleichung eines Linearfaktors mit einem Differenzenquotient.
- Dabei ist
- Bei den häufig vorkommenden Differenzengleichungen 1. Ordnung wird nur
eine Programmzeile für die Berechnung der aktuellen Ausgangsgröße
und die Programmzeile
der vorherigen Berechnung gespeichert. Jede Ausgangsgröße bezieht sich rekursiv auf die vorhergehende Ausgangsgröße als Eingangsgröße. Innerhalb einer Reihe von Differenzengleichungen einer Programmzeile ist die Ausgangsgröße einer Differenzengleichung die Eingangsgröße der nächsten Differenzengleichung der gleichen Programmzeile.
- Identifikation der Regelstrecke
- Über eine Identifizierung des zeitlichen Verhaltens der Regelstrecke
werden Übertragungsglieder
vorzugsweise als Linearfaktoren in Zeitkonstantendarstellung analysiert. Mittels eines Personal-Computers wird mit einer Simulation das Verhalten des Reglers und das der Strecke durch Berechnung von Differenzengleichungen bestimmt.
Weitere Vertiefung zur Systemidentifikation siehe Artikel Regelstrecke
- Simulation des Regelkreises
- Ob es sich bei der numerischen Berechnung eines dynamischen Systems um
einen digitalen Regler oder um eine Regelkreis-Simulation am Personalcomputer
mit vielen Differenzengleichungen von Teilsystemen handelt, besteht der
Unterschied nur darin, dass das Eingangssignal e(t) des digitalen Reglers mit
Hardware-Komponenten zu einer Eingangsfolge
mit der Abtastperiode
abgetastet werden muss.
- Bei der Simulation einer Regeleinrichtung wird in einem Personalcomputer
jedes einzelne dynamische System mit Differenzengleichung rekursiv berechnet.
Für jedes gegebene Eingangssignal wird mittels Differenzengleichungen einer
Programmzeile ein aktuelles Ausgangssignal
berechnet und bezieht sich dabei auf einen zurückliegenden Wert der Programmzeile
. Sämtliche dynamischen Teilsysteme einer Programmzeile bestimmen rekursiv im Abstand eines Zeitintervalls
einen Berechnungspunkt der Stellgröße
.
- Jedes dynamische Teilsystem ist innerhalb einer Programmzeile durch eine
Differenzengleichung beschrieben. Die Programmzeilen entsprechen endlichen
nummerierten Folgen
, die für einen Betrachtungszeitraum
eine Annäherung an das zeitverhalten
der Originalfunktion des Regelkreises darstellt.
- Sämtliche Ergebnisse aller Differenzengleichungen des Reglers, der
Regelstrecke, der Regelgröße und der Regelabweichung werden für
-Zeilen als Tabelle gespeichert.
- Parametrierung des digitalen Reglers
- Die Simulation eines Regelkreises und das Arbeiten eines Digitalreglers in Verbindung mit einer Regelstrecke sind in Bezug auf die Verwendung von Differenzengleichungen ähnlich.
- Eine Programmzeile beinhaltet je nach gewünschtem Regelalgorithmus mehrere Differenzengleichungen vorteilhaft in Produktdarstellung, weil differenziell wirkende Übertragungsglieder des Reglers die verzögernd wirkenden Übertragungsglieder der Regelstrecke kompensieren können. Damit wird die Parametrierung des Digitalreglers sehr vereinfacht, indem die Zeitkonstanten der differenzierenden Komponenten des Reglers denen der Verzögerungsglieder der Regelstrecke gleichgesetzt werden.
Wertefolge durch Abtastung von Signalen
In der Mathematik wird eine Auflistung von endlich und unendlich vielen fortlaufend nummerierten Objekten als Folge bezeichnet. Dasselbe Objekt kann in einer Folge auch mehrfach auftreten.
Die Abtastfolge
bedeutet eine Nummerierung der Folgeglieder der Wertefolge des Eingangssignals
(Eingangsfolge) und des Ausgangssignals (Ausgangsfolge) eines Systems.
Eine Wertefolge besteht aus
oder
vielen Folgegliedern. Das Objekt mit der Nummer i wird i-tes Folgeglied oder
i-te Komponente der Folge genannt.
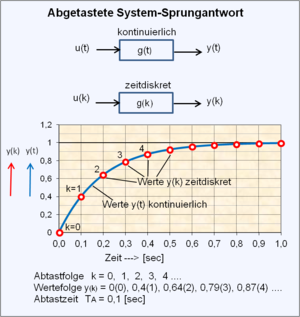
Die Signalabtastung kontinuierlicher Signale f(t) erfordert
Hardware-Komponenten wie idealisierte Abtaster (-Abtaster)
und A/D-Wandler, deren digitalisierte Signale
als Folgeglieder der Wertefolge im Mikrocomputer zu Stellgrößensignalen
verarbeitet werden.
Die Periodendauer einer kontinuierlichen Abtastfolge eines analogen oder
digitalisierten Eingangssignals wird meist mit
(auch
und
)
bezeichnet. Diese Funktion unterscheidet sich von der diskreten Zeit einer
Simulation eines dynamischen Systems am Computer dadurch, dass die Periodendauer
der Abtastung zu einer Wertefolge eine reale Zeit ist und kontinuierlich
zyklisch ohne eine begrenzte Anzahl von Folgegliedern wirkt. Die Werte des
zeitdiskreten Parameters
und der Abtastzeit
können identisch sein.
Eine Wertefolge mit
Folgegliedern können in einem digitalen Rechner gespeichert und aufgelistet
werden. Dies ist bei unendlich vielen Folgegliedern der Wertefolge, wie sie bei
Einsatz von digitalen Reglern auftreten, nicht möglich und auch nicht
erforderlich.
Im Online-Betrieb eines Digitalreglers ist die Anzahl
der Folgeglieder der Ein- und Ausgangsfolge unbegrenzt.
- Beispiel einer Regeldifferenz-Folge mit der Abtastzeit
:
- Abtastung der Regeldifferenz e(t) zu einer Wertefolge
des Regler-Eingangs:
- Bei der Berechnung der Folgeglieder der Eingangsfolge mit
Differenzengleichungen für den Berechnungsalgorithmus der Methode „Euler
Rückwärts“ werden nur zwei aktuelle Folgeglieder der Ausgangswertefolge
mit folgenden Indizierungen benötigt:
- Aktueller Wert des Folgegliedes der Ausgangsfolge
,
- Vorheriger Wert des Folgegliedes der Ausgangsfolge
.
- Aktueller Wert des Folgegliedes der Ausgangsfolge
- Mit der Berechnung der Folgeglieder der Eingangsfolge mit Differenzengleichungen ergeben sich die Werte der Folgeglieder der Ausgangsfolge des Reglers:
- Beispiel der Abtastfolge einer Sprungfunktion G(s) = 1 / s:
- Die normierte Signaleingangsgröße e(t) hat den Wert 1.
- Die Wertefolge der Sprungfunktion hat die Werte:
- Beispiel der Wertefolge einer
-Impulsfunktion:
- Die normierte Signaleingangsgröße e(t) des
-Impulses hat den Wert 1 für die Folge Null. Alle anderen Werte der Folgen betragen Null.
- Abtastfolge
- Wertefolge
- Anmerkung: Bei Anwendung von Differenzengleichungen nach dem Verfahren
Euler-Rückwärts mit der Funktion der Obersumme hat das Folgeglied des
-Impulses zum Zeitpunkt t = 0 und k = 0 den Wert
. Differenzengleichungen der Untersumme können diesen Wert
nicht erfassen.
Abtasttheorem
Bei einem idealen Abtaster (Sampler) in Verbindung mit einem A/D-Wandler wird aus einem analogen Signal eine Zahlenfolge, die jeweils in einen zeitlichen Abstand TA generiert wird. Liegen die digitalisierten Abtastwerte bezogen auf die Dynamik des Analogsignals bei hoher Abtastfrequenz dicht bei einander, folgt das digitalisierte Signal genau dem Verlauf des Analogsignals. Damit gehen durch die Abtastung wenig Informationen verloren.
Je nach verwendetem Mikrorechner erlauben schnelle Regelstrecken keine beliebig hohen Auflösungen des Abtastvorgangs eines Analogsignals, weil sowohl die Grenzfrequenz der Schnittstellen erreicht wird, als auch der Mikrorechner die Rechenleistung nicht mehr bringen kann.
In der Praxis bestehen reale Signale aus einem Gemisch vieler Frequenzen.
Nun stellt sich die Frage, welche Mindest-Abtastfrequenz
ist erforderlich, dass beispielsweise ein analoges sinusförmiges Signal
ohne größeren Informationsverlust abgetastet werden kann. Ein harmonisches
sinusförmiges Signal ist durch Abtastung vom Original und Rekonstruktion nicht
zu unterscheiden, wenn die Abtastfrequenz
mindestens doppelt so hoch ist, wie die Originalfrequenz
.
Dieser Zusammenhang wurde bereits von dem Physiker Harry Nyquist als
sogenannte Nyquist-Frequenz
erkannt.
Das Nyquist-Shannon-Abtasttheorem
besagt, dass ein harmonisches analoges auf
bandbegrenztes Frequenzsignal mit einer Frequenz von mindestens
abgetastet werden muss, damit man es aus dem zeitdiskreten Signal wieder exakt
rekonstruieren kann.
Durch Frequenzüberlagerungen wie Signalstörungen können bei der
Rekonstruktion des abgetasteten Signals erhebliche Unterschiede zum analogen
Signal auftreten. In der Praxis müssen deshalb zur Vermeidung von
Fehlinterpretationen dem A/D-Wandler ein vorgeschaltetes Tiefpassfilter (Anti-Aliasing-Filter)
zur Reduzierung höherer Frequenzanteile vorgesehen werden. Damit das
Tiefpassfilter keine zu steilen Flanken aufweisen muss, wählt man eine
Abtastfrequenz ,
die wesentlich über dem theoretischen Wert
liegt. In der Praxis wählt man als Abtastfrequenz
5- bis 10-mal
.
Wird die zweifache Menge der Abtastfrequenz von fmax unterschritten, kommt es zu dem Alias-Effekt (auch Aliasing-Effekte oder kurz Aliasing).
Regelung im Offline- und Onlineprozess
Völlig unterschiedliche Verfahren der Anwendung der numerischen Berechnung sind bei der Simulation eines dynamischen Systems z.B. eines Regelkreises oder eines digitalen Reglers, der auf eine analoge, kontinuierliche Regelstrecke wirkt, zu unterscheiden.
Simulation von Regelkreis-Systemen (Offline-Prozess)
Dynamische Systeme wie Regelkreise, Regelstrecken und Regler können aus verschiedenen Teilsystemen mit unterschiedlichem Zeitverhalten als Reihenschaltung, Parallelschaltung oder als zurückgeführte Kreisschaltung bestehen.
Für die Berechnung des Eingangs-Ausgangsverhaltens von Übertragungssystemen oder der Simulation von Regelkreisen bieten sich käufliche Rechenprogramme an. Mit den bekannten Programmen wie MATLAB und Simulink stehen umfangreiche Befehlssätze für die theoretische Modellierung von dynamischen Systemen und vielen speziellen regelungstechnischen Befehlen zur Verfügung.
Alternativ können mit selbst erstellten beliebigen Rechenprogrammen für Differenzengleichungen mit der diskreten Zeit Δt (auch Abtastzeit TA) in Verbindung mit logischen Operationen sehr effizient lineare und nichtlineare System-Simulationen durchgeführt werden.
Lineare dynamische Systeme, wie auch die Komponenten des Regelkreises, werden
im Zeitbereich
mit Differenzialgleichungen und im s-Bildbereich anschaulich als
Übertragungsfunktion
beschrieben. Die elementaren dynamischen Teilsysteme der Übertragungsfunktion
lassen sich aus den Zähler- und Nennerpolynomen der Übertragungsfunktionen
mittels der Nullstellenbestimmung in Faktoren (Linearfaktoren) zerlegen. Damit
entstehen die bekannten vier Elementarsysteme erster Ordnung, I-Glied, D-Glied,
PT1-Glied und PD1-Glied des Bildbereichs, die im Zeitbereich durch
Differenzialgleichungen beschrieben werden. Durch Austausch der
Differentialquotienten durch Differenzenquotienten entstehen die
Differenzengleichungen des zeitdiskreten Bereichs
.
Mit der Anwendung von Differenzengleichungen ist eine mathematische
Näherungsmethode in kleinen Zeitschritten
gegeben, die eine erhebliche Vereinfachung für das Lösen von
Differenzialgleichungen bedeutet.
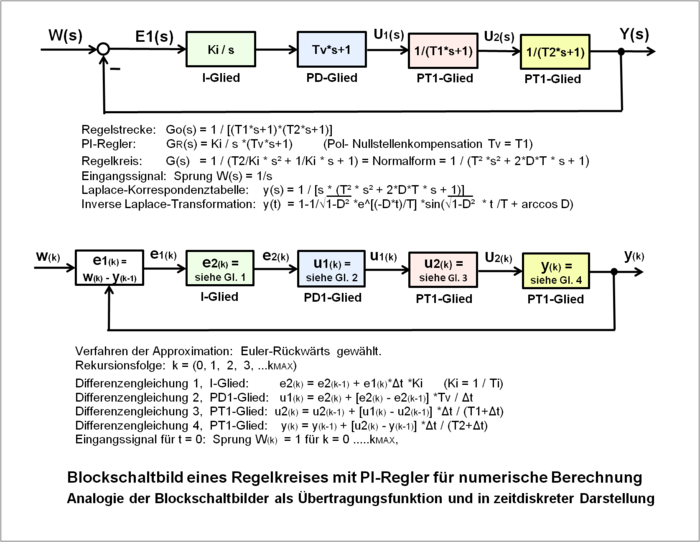
Die Berechnung des Ausgangssignals eines dynamischen Systems oder eines Regelkreises für ein gegebenes Eingangssignal erfolgt in einem Digitalrechner (Personal Computer). Dazu werden die Elementarsysteme eines Gesamtsystems in Abhängigkeit von einem Eingangssignal mit Differenzengleichungen hintereinander berechnet, in der Weise, dass ein Ausgangssignal eines Elementarsystems das Eingangssignal des folgenden Elementarsystems ist. Sämtliche Ergebnisse der Teilsysteme bis zum Ausgangssystem werden als eine Berechnungszeile dargestellt.
Handelt es sich bei dem Gesamtsystem um die Simulation eines Regelkreises, so
werden hintereinander in einer Zeile sämtliche Teilsysteme des Gesamtsystems
durch Differenzengleichungen des Reglers und der Regelstrecke für je ein
Folgeglied berechnet. Das Ausgangsfolgeglied entspricht einem Berechnungswert
der Regelgröße .
Alle berechneten Teilsysteme für je ein Folgeglied beziehen sich auf den
gleichen Wert von k und auf den vorherigen Wert k-1. Das so berechnete
Folgeglied der Regelgröße entspricht der Behandlung eines offenen Regelkreises.
Der Regelkreis wird geschlossen mit der Beziehung der Regelabweichung
,
die am Anfang der Berechnungszeile steht.
Danach erfolgt mit der nächsten Berechnungszeile die gleiche Berechnung der Einzelsysteme des Gesamtsystems als nächstes Folgeglied mit der nächsthöheren Folgenummer von k. Jedes einzelne zu berechnende Folgeglied laut der verwendeten Differenzengleichungen innerhalb dieser Zeile bezieht sich wieder auf das vorhergehende Folgeglied k-1.
Damit ergeben sich insgesamt
Zeilen und Folgeglieder:
Das Berechnungsergebnis ist eine im Rechner gespeicherte Tabelle, deren
Spalten z.B. hintereinander die Rechenergebnisse der einzelnen Teilsysteme
wiedergibt, die Zeilen entsprechen der Anzahl der Folgeglieder von
bis
und enthalten identische Gleichungen.
Die erste Zeile der Gleichungen der Regelabweichung sowie aller Teilsysteme des Reglers und der Regelstrecke wird einmal festgelegt und je nach gewünschter Auflösung der Regelgröße der Daten 100-1000-fach kopiert. Aus diesen Daten lässt sich automatisch eine Grafik für den Verlauf von y(t) oder jedes andere Teilergebnis generieren.
Das Ergebnis ist ein gespeichertes tabellarisches Protokoll sämtlicher Berechnungszeilen und Berechnungspunkte der Teilsysteme und der Systemausgangsgröße.
Enthält die Regelstrecke eine Totzeit ,
kann diese durch geeignete Programmbefehle – Rückwärtsverschiebung der
Folgeglieder der Wertefolge um
-Schritte – der Regelstrecken-Nachbildung berücksichtigt werden.
Dieser Rechenvorgang mit dem Ergebnis einer tabellarischen Aufstellung der
Berechnungszeilen mit den Folgegliedern der Abtastfolge von
bis
ist nicht zeitabhängig, sondern je nach Rechengeschwindigkeit des Rechners steht
das Gesamt-Rechenergebnis unmittelbar zur Verfügung. Die diskrete Zeit
zwischen den Folgegliedern der Abtastfolge
und
ist als Parameter (Zahlenwert) in den Differenzengleichungen berücksichtigt und
ist keine reale Zeit.
Eine zeitlich geschlossene Stufung (Rechteckverlauf) der Ausgangsgrößen ist
nicht erforderlich. In einem Diagramm
kann der Verlauf der Ausgangsgröße bei genügender Anzahl von Folgegliedern der
Wertefolge (Berechnungspunkte) als geschlossene Linie für den Zeitraum
dargestellt werden.
Wird ein Regelkreis mit diesem Verfahren behandelt, was voraussetzt, dass ein mathematisches Modell der Regelstrecke vorliegt, handelt es sich um eine Regelkreis-Simulation, die bestens für den Regler-Entwurf zur Auffindung der erforderlichen Reglerparameter geeignet ist.
Beliebige Rechenprogramme können verwendet werden. Es empfiehlt sich die Nutzung der Tabellenkalkulation, weil damit Programmierungsfehler ausgeschlossen sind und eine grafische Darstellung der Signalverläufe eingebunden ist.
Digitale Regler für analoge kontinuierliche Regelstrecken (Online Prozess)
Enthalten Regelkreise Systeme, die ihre Signale nur zu diskreten Zeitpunkten übertragen, handelt es sich um zeitdiskrete Regelsysteme oder Abtastregelungen. Die Abtastung von Signalen kann meist kontinuierlich, aber auch zufällig oder nach einer Regel erfolgen.
Bei kontinuierlichen Systemen beschreiben Differenzialgleichungen das Systemverhalten, bei zeitdiskreten Systemen sind es die aus den Differenzialgleichungen abgeleiteten Differenzengleichungen, die eine zeitdiskrete Abtastung und Berechnung des System-Eingangssignals entsprechend der Systemdynamik zu einer Ausgangsgröße möglich machen.
Die fortlaufende Abtastung des Eingangssignals wird mit Abtastfolge bezeichnet. Jedes Folgeglied der Abtastfolge entspricht einem Wert, der in einem Mikrocomputer zu einem Stellgrößenwert innerhalb der Ausgangsfolge berechnet wird.
Digitale Regler wie auch analoge Regler benötigen ein Signal der
Regelabweichung von der Führungsgröße minus der zurückgeführten Regelgröße. Die
verwendeten Mikrocomputer (Mikrocontroller)
erfordern zur Berechnung der meist analogen Signale geeignete Eingangs- und
Ausgangsschnittstellen. Diese sind in der Regel Analog-Digital-Umsetzer
(A/D-Wandler), die zu diskreten Zeitpunkten das Eingangssignal abtasten und
digitalisieren. Das Ergebnis der Signalabtastung der Regelabweichung kann man
auch als modulierte Delta-Impulsfolgen für
bis
unterschiedlicher Amplituden ansehen.
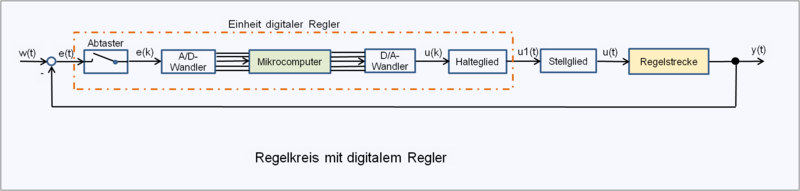
• Der Mikrocomputer berechnet mit Differenzengleichungen zeitsynchron die Wertefolgen des Eingangs zu Ausgangsfolgen.
• Ein Glied der Ausgangsfolge des Mikrocomputers ist ein Berechnungspunkt in Annäherung an die analytische Funktion.
• Aufgabe des Stellgliedes ist die Energie-Versorgung, die ein Zeitverhalten haben kann.
• Der Einfluss von Störgrößen innerhalb der Regelstrecke wird im Artikel Regelkreis behandelt.
Die Ausgabe der nach einem Regelalgorithmus berechneten digitalen Signale erfolgt über einen Digital-Analog-Umsetzer (D/A-Wandler), dem ein Halteglied (Sample-and-Hold-Verfahren) nachgeschaltet ist. Durch die Haltestufe wird das Ausgangssignal bis zum nächsten Folgeglied der Ausgangsfolge gehalten, damit ein analoges gestuftes Regler-Ausgangssignal an eine Leistungs-Schnittstelle der Stelleinrichtung zur Regelstrecke weitergegeben werden kann. Die abgetastete Eingangsgröße der Eingangsfolge muss ebenfalls solange gehalten werden (schnelle Haltegliedfunktion), bis die Digitalisierung des Eingangssignals und die Übergabe in den Mikrocomputer abgeschlossen ist. Mit dieser Maßnahme kann das digitale Ausgangssignal als ein kontinuierliches, gestuftes, quasi-analoges Ausgangssignal gewandelt und über einen Leistungsteil als Stellgröße an die Regelstrecke überführt werden.
Durch den Abtaster und den A/D-Wandler ist eine Quantisierung des
Eingangssignals zu einer Signal-Impulsfolge (Zeitquantisierung) und der
Amplitude (Amplitudenquantisierung) verbunden. Der Microcomputer bearbeitet und
berechnet die digitalisierten Signalfolgen der Eingangsgröße
zu einer digitalen Ausgangs-Stellgrößen-Folge
.
Die Aufgabe des Digitalreglers innerhalb eines Regelkreises besteht darin, das Eingangssignal der Regelabweichung nach jeder Abtastung mittels Differenzengleichungen und logischer Befehle als Regelalgorithmus so zu berechnen, dass das Ausgangssignal der Regelstrecke, die Regelgröße, sich nach einem gewünschten meist asymptotisch stabilen Verlauf der Führungsgröße annähert.
Die für die Festlegung des dynamischen Verhaltens des Reglers benötigten
Differenzengleichungen als Funktion der diskreten Zeit und der Abtastfolge
entstehen nach dem einfachsten Verfahren der Methode Euler-Rückwärts,
indem die Differentialquotienten der System-Differenzialgleichung des Reglers
durch Differenzenquotienten ersetzt werden.
Ein Digitalregler ist ständig im Einsatz und führt damit eine unbegrenzte
Anzahl von berechneten Folgegliedern der Ausgangsfolge durch. Der Rechner muss
für die Berechnung mit Differenzengleichungen (Methode Euler-Rückwärts) für die
Berechnung der Folgeglieder der Ausgangsfolge – aus den Gliedern der
Eingangsfolge – stets ein Folgeglied der Folge
(aktueller Wert) und das Folgeglied der zurückliegende Folge
(vorheriger Wert) zur Verfügung stellen.
Zur digitalen Verarbeitung wird der Zeitraum zwischen zwei Folgegliedern der
Berechnungsfolgen anstelle der Parameters der diskretisierten Zeit
meist mit der Abtastzeit
(auch
oder
)
bezeichnet, die einer realen Zeit entspricht. Das mit der Abtastfrequenz
abgetastete und digitalisierte Eingangssignal
wird zur Folge
mit den Differenzengleichungen der Ausgangssignale der Form
als Regleralgorithmus berechnet.
Differenzengleichungen des Regelalgorithmus des Digitalreglers berechnen die
abgetasteten Eingangssignale :
fortlaufend mit jeder Abtastung unbegrenzt. Der Mikrocomputer verarbeitet mit
Hilfe eines Abtasters und A/D-Wandlers aus der analogen Regelabweichung
Folgeglieder der Eingangsfolge, die zeitsynchron mit der Abtastzeit
abgetastet und berechnet werden.
Die Berechnung der Eingangsfolge mit Differenzengleichungen ergibt die Ausgangsfolge:
.
Da die Regelstrecke meistens ein kontinuierliches analoges Verhalten hat,
erfolgt am Mikrocomputer-Ausgang eine D/A-Wandlung der digitalen Ausgangsgröße
mit nachgeschaltetem Halteglied der Dauer .
Damit entsteht im Abstand
aus den errechneten Folgegliedern als Stellgröße ein quasi stetiges, gestuftes,
analoges Signal.
Jede Abtastung wie auch der Rechenvorgang selbst benötigt eine endliche Zeit, bis eine Steuerung oder Berechnung innerhalb der Abtastfolge durchgeführt werden kann. Damit ergibt sich durch dieses Zeitverhalten gegenüber dem Originalverlauf der Eingangsgröße eine nacheilende Zeitverschiebung, die sich als Totzeit bemerkbar macht. Ob diese Totzeit vernachlässigbar ist, hängt von der Größe der dominanten Zeitkonstante der Regelstrecke ab.
Der Vorteil der zunehmend eingesetzten digitalen Regler gegenüber analogen Reglern ist:
- Einmaliger Entwicklungsaufwand der Hardware
- vielseitige Anpassung an beliebige komplexe Regelaufgaben per Software,
- Vorteil der komplexen Reglerstrukturen:
- Zustandsregler, adaptive Regler, Prädiktorregler, dead-beat-Regler, Multitasking mit einem Regler für verschiedene Regelstrecken,
- große statische Genauigkeit realisierbar, falls gefordert,
- Kosten-Nutzen-Vorteil insbesondere in Anlagen hoher Stückzahlen, die bei Parameter- oder Strukturänderungen keine Hardware-Änderungen erforderlich machen.
- Hochintegrierte Microcomputer für die Anwendung regelungstechnischer Aufgaben mit den Funktionen wie Abtastgliedern, A/D-Wandlern, D/A-Wandlern und Haltestufen sind bereits kommerziell verfügbar.
Nachteile der digitalen Regler:
- Quantisierungsfehler können auftreten,
- durch Abtastung und Rechenzeit verbundene Totzeit,
- Material- und Zeitaufwand bei kleiner Stückzahl.
Begriffsklärung der numerischen Berechnung
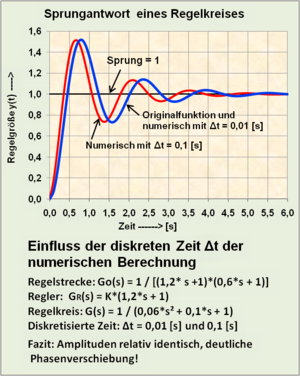
Diskrete Zeit
Es werden hier zur Kennzeichnung der physikalischen Unterschiede der Zeitdiskretisierung folgende Definitionen festgelegt:
ist ein Parameter der diskreten Zeit, keine reale Zeit.
wird z.B. bei der Berechnung der Differenzengleichungen verwendet.
(auch
oder
) ist eine reale Zeit, mit der ein kontinuierliches Signal im Takt von
abgetastet wird.
Die Zeitdiskretisierung eines dynamischen zeitinvarianten Übertragungssystems
bedeutet der Übergang der Berechnung eines kontinuierlichen Systems
mit unendlicher hoher Auflösung zu einem System
mit einer endlichen Auflösung eines fortlaufenden konstanten Zeitintervalls
.
Die Folge
beschreibt eine endliche Zahl der Folgeglieder für eine numerische Berechnung
(Simulation) am Computer.
Das Zeitintervall
muss genügend klein sein, damit dominante Systembewegungen auch erfasst werden
können, bzw. der Approximationsfehler gegenüber dem Verlauf der analytischen
Funktion gering ist. Das Intervall
muss kleiner sein als der Parameter der kleinsten Systemzeitkonstante
,
anderenfalls ergeben sich Berechnungsfehler.
sollte ein Hundertstel bis ein Tausendstel der dominanten Systemzeitkonstante
betragen.
Regelalgorithmus digitaler Standardregler (Euler-Rückwärts)
In der Offline- und Online-Anwendung für die Standardregler können die Differenzengleichungen der einfachsten Form nach dem Streckenzugverfahren „Euler-Rückwärts“ angewendet werden.
Dieses Verfahren hat den Vorteil, mit einfachen Differenzengleichungen zu
operieren, hat aber den Nachteil bei der Online-Anwendung, dass mit kleiner
werdender Abtastzeit
und steigender geforderter Genauigkeit die Anzahl der rekursiven Berechnungen
für einen festen Beobachtungszeitraum umgekehrt proportional größer wird.
Unabhängig davon vergrößert sich mit der kleiner werdenden Abtastzeit das
Verhältnis zur Ersatztotzeit (Digitalisierung, Rechenzeit, Halteglied) der
Hardware-Schnittstellen. Ob damit ein Zeit- und Kostenproblem vorliegt, hängt
davon ab, wie groß die dominante Streckenzeitkonstante, die Abtastzeit der
Regelabweichung und die Reaktionszeit der verwendeten Hardware-Bauelemente des
Reglers sind.
Numerische Stabilität
Für die numerische Stabilität und der Berechnungsgenauigkeit der Simulation
gelten zwei Bedingungen: Zur Vermeidung der numerischen Instabilität kann die
Verstärkung nicht unbegrenzt hoch gewählt werden, wenn es auch theoretisch bei
stetig wirkenden Regelkreisen bis zu zwei Verzögerungsgliedern möglich wäre.
Bedingung: Bei sehr großer Kreisverstärkung
einer Regelkreisnachbildung muss
kleiner als
sein.
ist das Produkt aller Einzelverstärkungen,
ist die dominante Systemzeitkonstante.
ist die kleinste Systemzeitkonstante.
Genauigkeit der numerischen Simulation
Die Genauigkeit der numerischen Berechnung eines dynamischen Systems
gegenüber der analytischen Funktion bei Anwendung des Euler-Rückwärts-Verfahrens
steigt linear mit dem kleiner werdenden Zeitintervall
im Verhältnis zur dominanten Systemzeitkonstante
.
Der Approximationsfehler
im Vergleich zur analytische Funktion beträgt
.
Das Zeitintervall
muss kleiner als die kleinste zu berechnende Systemzeitkonstante betragen.
Anderenfalls treten zusätzliche Fehler auf.
.
Differenzengleichungen linearer zeitinvarianter Übertragungssysteme
Grundlagen Systemverhalten
Ein System ist eine Funktionseinheit mit mindestens einem Signaleingang und einem Signalausgang. Hat das System ein zeitliches Verhalten durch meist konzentrierte Energiespeicher, wird es als dynamisches System bezeichnet. Statische Systeme haben keine Energiespeicher und damit kein Zeitverhalten.
Dynamische Systeme werden durch verschiedene Formen von Differentialgleichungen beschrieben. Nicht alle Differentialgleichungen sind einfach analytisch lösbar.
Technische Systeme können sich zeitabhängig, zeitunabhängig, linear, nichtlinear, kontinuierlich und diskontinuierlich verhalten. Das gut angenäherte Eingangs- Ausgangsverhalten dieser Systeme kann durch Differenzengleichungen numerisch relativ einfach mit Computern gelöst werden.
Handelt es sich um kontinuierliche dynamische Systeme, wird das Zeitverhalten
mit Hilfe von Differenzengleichungen
durch zeitdiskretes Verhalten ersetzt. Durch die Diskretisierung der Signale
entstehen mittels punktueller Abtastung die Eingangs- und Ausgangswertefolgen im
zeitlichen Abstand .
Differenzengleichungen beziehen sich allgemein auf die Differentialquotienten
einer gewöhnlichen Differentialgleichung, die durch Differenzenquotienten
ersetzt werden und damit entsteht eine numerisch lösbare Differenzengleichung in
Annäherung an die Differentialgleichung.
Nichtlineare und lineare dynamische Systeme können mit geeigneten Differenzengleichungen kombiniert werden. Die Nichtlinearität wird durch logische Funktionen oder Tabellenwerte definiert.
Differenzengleichungen können sich auch auf statische, zeitunabhängige Systeme beziehen, in dem die Systemeingangsgröße diskretisiert und das Systemausgangsverhalten durch logische Funktionen berechnet wird.
Beispiele von linearen, nichtlinearen und zeitunabhängigen Systemen
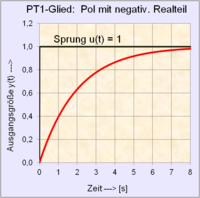
| Sprungantwort Lineares System 1. Ordnung, Pol = negativ real |
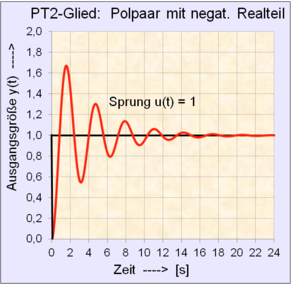
Sprungantwort Lineares System 2. Ordnung mit konjugiert komplexen Polen |
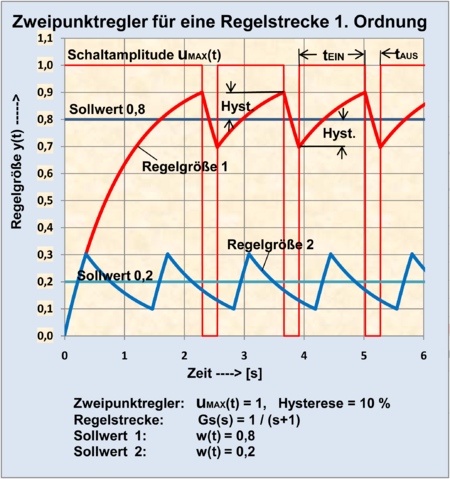
Nichtlineares System (Schaltregler mit Hysterese und lineares System 1. Ordnung) |
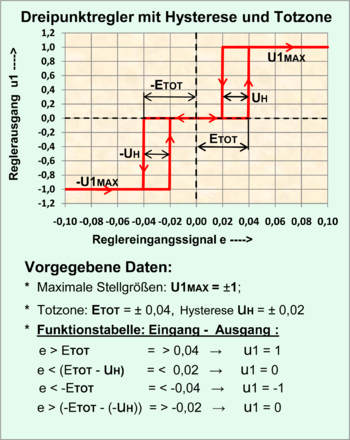
Zeitunabhängiges System (Dreipunktregler mit Hysterese und Totzone) |
|---|---|---|---|
|
|
|
|
| Lösung mit Differenzengleichung 1. Ordnung |
Lösung mit Differenzengleichung 2. Ordnung |
Berechnung mit log. Befehlen und Differenzengleichung 1. Ordnung |
Berechnung mit log. Befehlen: WENN-DANN-SONST-Anweisung |
Grundlagen der Differenzengleichungen linearer zeitinvarianter Systeme
Es bestehen verschiedene mathematische Verfahren, zeitkontinuierliche Systeme in zeitdiskrete Systeme zu beschreiben und umzuwandeln.
Differenzengleichungen entstehen meist aus einer systembeschreibenden gewöhnlichen Differenzialgleichung, deren Differentialquotienten durch Differenzenquotienten ersetzt werden. Die kontinuierlichen mathematischen Operationen der Integration und Differentiation werden zeitdiskret durch Summen- und Differenzenbildung angenähert.
Differenzengleichungen berechnen in Abhängigkeit von einer Eingangswertefolge
und dem dynamischen System die Ausgangswertefolge mit der Folge ,
die eine Nummerierung der Werte darstellt.
Zu unterscheiden ist die Anwendung einer Simulation eines zeitdiskreten
dynamischen Systems in Abhängigkeit von einem Eingangssignal und die Anwendung
eines realen Hardwaresystems, dessen Eingangssignal im zeitlichen Abstand
abgetastet wird.
- Simulation: Für die Anwendung einer Simulation am Digitalrechner
wird das Eingangssignal für den Zeitparameter
diskretisiert und mit der Differenzengleichung des dynamischen Systems wird die Ausgangsfolge für
berechnet. Diese rekursive Differenzengleichung bezieht sich immer auf zurückliegende Ausgangswertefolgen und wird beliebig oft - je nach geforderter Genauigkeit - neu berechnet. Das Ergebnis ist eine tabellarisch im Rechner gespeicherte Folge von Werten (Berechnungspunkte) im zeitlichen Abstand
, welche auch grafisch als Funktion des diskreten Eingangssignals und des Systemübertragungsverhaltens dargestellt werden kann.
- Signalabtastung: Bei einem gegebenen Hardwaresystem wird das
Eingangssignal im zeitlichen Abstand der Abtastzeit
abgetastet, digitalisiert und als Eingangswertefolge in einen Mikrorechner geleitet. Meist handelt es sich bei diesem System um den Regelalgorithmus als Differenzengleichung. Die Ausgangsfolge wird analogisiert und in ein Halteglied z.B. nullter Ordnung geleitet. Damit entsteht ein gestuftes quasi stetiges Signal, das als Stellgröße von einer kontinuierlich wirkenden Regelstrecke verarbeitet werden kann.
Die Differenzengleichungen beschreiben mit dem Approximationsalgorithmus für
ein kleines Zeitintervall
die Signaländerungen am Ausgang eines Systems
(vereinfachte Schreibweise
)
nach jedem Zeitintervall als Funktion des betreffenden Systems (z.B.
Linearfaktoren im s-Bereich) und des Eingangssignals
.
Mit der fortlaufenden Wiederholung der Berechnung mit dem Zeitintervall
und Addition der Änderungsergebnisse zum vorherigen Ergebnis
ergibt sich der Signalverlauf eines Systems
über die Zeit
.
Die Lösung des Systemverhaltens eines dynamischen Systems mit Differenzengleichungen entspricht immer der Gesamtlösung als Addition der homogenen und partikulären Lösung. Ohne Anfangswerte handelt es sich um die partikuläre Lösung. Sind Anfangswerte des Systems vorhanden, kann die Regelungsnormalform der Zustandsraumdarstellung zur Lösung mit Differenzengleichungen des Systems herangezogen werden. In den Differenzengleichungen ohne Anfangswerte ist die Lösungsvorschrift bereits enthalten.
Differenzengleichungen können auch mit Hilfe der z-Transformation entstehen.
Linearfaktoren der Übertragungsfunktion G(s)
Differenzengleichungen der einfachsten Art beziehen sich auf die den Linearfaktoren der Übertragungsfunktion G(s) zugehörigen Differenzialgleichungen erster Ordnung, deren Differentialquotienten durch Differenzenquotienten ersetzt werden.
Linearfaktoren entstehen durch Nullstellenzerlegung von Polynomen des Zählers und Nenners einer Übertragungsfunktion G(s) als gebrochen-rationale Funktion. Diese Beziehung ist von großer Bedeutung, weil insgesamt nur drei verschiedene Formen von Linearfaktoren erster und zweiter Ordnung auftreten und Systeme höherer Ordnung nur Kombinationen davon enthalten.
Mittels der Nullstellenbestimmung
können die Polynome der Übertragungsfunktion
in eine Produktform (Linearfaktoren)
im Zähler und Nenner gebracht werden. Die Pole (Nullstellen des Nenners) oder
Nullstellen (Nullstellen des Zählers) sind entweder Null, reell oder konjugiert
komplex. Die Produktdarstellung im Zähler und Nenner der
Übertragungsfunktion
ist mathematisch identisch mit der Polynomdarstellung im Zähler und Nenner.
Für die Nullstellenbestimmung eines Polynoms bis 4. Ordnung sind im Internet
fertige Programme unter dem Aufruf „Nullstellen (Lösungen) von Polynomen
bestimmen“ zu finden. Für Systeme 2. Ordnung kann die „pq-Formel“:
verwendet werden zur Berechnung von
der konjugiert komplexen Nullstellen.
Linearfaktoren der Pol-Nullstellendarstellung
Beispiel der Zerlegung der Polynome der Übertragungsfunktion durch die Pol- Nullstellungbestimmung in reelle Linearfaktoren:
Da die Linearfaktoren des Zählers und Nenners der Übertragungsfunktion
identisch sind, werden die Nullstellen und Polstellen zur vereinfachten
Darstellung mit
bezeichnet. Negative Realteile der Pole und Nullstellen der Linearfaktoren
bedeuteten stabile Elementarsysteme, positive Realteile bedeuten instabile
Elementarsysteme.
- Bei Linearfaktoren 1. Ordnung sind die Nullstellen
oder Pole
reelle Zahlenwerte. Stabile Systeme enthalten negative Realteile.
- Linearfaktoren 2. Ordnung mit konjugiert komplexen Nullstellen oder Polen werden zur einfacheren Berechenbarkeit zu quadratischem Termen zusammengefasst, in denen nur reelle Koeffizienten auftreten.
- Linearfaktoren werden meist in die Zeitkonstanten-Darstellung durch Reziprokbildung der Nullstellen und Pole umgerechnet.
- Produktterm in der Zeitkonstanten-Darstellung mit negativem Wert der
Nullstelle
:
In der linearen Regelungstechnik ist es eine willkommene Tatsache, dass praktisch alle vorkommenden regulären (phasenminimalen) Übertragungsfunktionen bzw. Frequenzgänge von Regelkreisgliedern auf folgende drei Grundformen (Linearfaktoren) geschrieben bzw. zurückgeführt werden können. Sie haben eine völlig unterschiedliche Bedeutung, je nachdem ob sie im Zähler (differenzierendes Verhalten) oder im Nenner (verzögernd, Integrierend) einer Übertragungsfunktion stehen.
In Abhängigkeit von den Zahlenwerten der Koeffizienten a und b der Polynom-Darstellung können die Produkte folgende drei Formen in der Zeitkonstanten-Darstellung annehmen:
-
Typ Linearfaktor Bedeutung im Zähler Bedeutung im Nenner
(Nullstelle = 0)Differenzierer, D-Glied Integrator, I-Glied
(Nullstelle reell)PD-Glied Verzögerung, PT1-Glied
(Nullstellen konjugiert komplex)PD2-Glied: für 0 < D < 1 Schwingungsglied PT2-Glied: für 0 < D < 1
- Dabei ist T die Zeitkonstante, s die komplexe Frequenz, D der Dämpfungsgrad.
- Die Übertragungsfunktion
eines dynamischen Übertragungssystems kann einfache und mehrfache Linearfaktoren im Zähler und Nenner enthalten.
Weitere Vertiefung zu Differentialgleichungen, Übertragungsfunktionen,
Entstehung der Linearfaktoren siehe Regelungstechnik
Entstehung der Differenzengleichungen
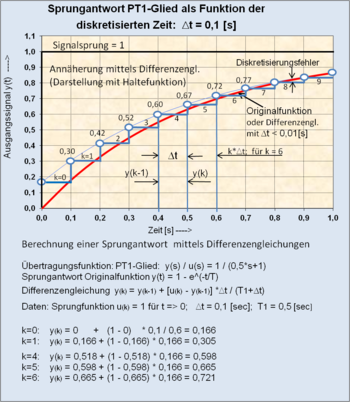
Meistens wird zur Aufstellung der Differenzengleichungen das explizite
Euler-Rückwärtsverfahren der Rechteckapproximation als einfachstes Verfahren
verwendet. Nach diesem Verfahren können aus den zugehörigen
Differenzialgleichungen der 4 Elementarsysteme G(s) erster Ordnung der
Übertragungsfunktionen Differenzengleichungen gebildet werden, indem an Stelle
des Differenzialquotienten mit
der Differenzenquotient
näherungsweise eingeführt wird.
In der Regel wird davon ausgegangen, dass die inneren Systemspeicher des
Übertragungssystems sich im Ruhezustand befinden und die Anfangswerte bei t = 0
für
und alle Ableitungen von
Null sind.
Die Ausgangsgröße eines berechneten zeitdiskreten Systems mit Hilfe von
Differenzengleichungen
wird in vereinfachter Schreibweise der Indizierung als
benannt.
Bei der Offline-Anwendung – beispielsweise die Simulation eines
Regelkreises mit
als Eingangsfolge und
als Ausgangsfolge – sind die Folgeglieder der Wertefolge auf eine bestimmte
Anzahl
begrenzt und beziehen sich auf den Zeitraum
.
Nach der Berechnung der Folgeglieder der Eingangsfolge
mit Differenzengleichungen entsteht die Ausgangsfolge mit ihren Folgegliedern
als Lösung in Annäherung an die zugehörige Differenzialgleichung.
Die Folgeglieder entstehen ohne Abtastung. Durch die rekursive Anwendung der
Differenzengleichung bezieht sich jede Berechnung
auf das zurückliegende Ergebnis
.
Die wiederholte Anwendung der gleichen Differenzengleichungen endet bei
.
Bei der Online-Anwendung mit einem digitalen Regler wird die
abgetastete Eingangsfolge
mit Differenzengleichungen berechnet, dann entstehen die Folgeglieder der
Ausgangsfolge des Reglers
.
Die Berechnung erfolgt mit digitalisierten Werten zeitsynchron im Takt von
.
Meist wird für die Regelstrecke ein kontinuierliches Stellsignal benötigt.
Wertefolgen können mit Hilfe eines A/D-Wandlers und eines Haltegliedes zu einem
gestuften quasi kontinuierlichen Signal gewandelt werden.
Der Nachteil des Euler-Rückwärts-Verfahrens ist für schnelle Regelstrecken bei guter Approximation an die analytische Systemfunktion die hohe Zahl der Abtastfolgen, die in der Offline-Simulation eines dynamischen Systems mit einem Digitalrechner keine Rolle spielt, dafür aber im Online-Betrieb. Mit steigender Genauigkeit der Approximation an das Übertragungsverhalten des Systems muss die Periodendauer der Abtastung kleiner werden und die Rechenleistung steigt linear an.
Andere Methoden der numerischen Berechnung bedienen sich zur besseren Approximation z.B. an Stelle des Rechteck-Verfahrens (Explizites Eulerverfahren) des Trapezflächenverfahrens (Heun-Verfahren), des Mehrschrittverfahrens (Runge-Kutta-Verfahren) und anderer Verfahren. Grund der aufwendigeren Approximationsverfahren und damit der umfangreicheren Differenzengleichungen ist die erzielbare höhere Genauigkeit und damit Reduzierung der Rekursionsfolgen, was bei langsamen Mikrocomputern und dessen Schnittstellen bei Echtzeitberechnungen erforderlich sein kann.
Beispiel der Entstehung einer Differenzengleichung der Integration (I-Glied) aus der Differenzialgleichung:
| Die Übertragungsfunktion des I-Gliedes lautet:
Die zugehörige Differenzialgleichung lautet: Der Differenzenquotient wird an Stelle des Differenzialquotienten Damit lautet die nach In gleicher Weise können die Differenzengleichungen der Standardregler aus den zugehörigen Differenzialgleichungen abgeleitet werden. |
| Elementarsysteme | Übertragungsfunktion | Differenzengleichungen |
|---|---|---|
| P-Glied | ||
| I-Glied | ||
| D-Glied | ||
| PD1-Glied | ||
| PT1-Glied |
(Mit K = Verstärkungsfaktor,
= aktuelle zeitdiskrete Ausgangsgröße,
= vorherige Ausgangsgröße, T = Zeitkonstante,
= aktuelle zeitdiskrete Eingangsgröße)
Diese Differenzengleichungen von Elementarsystemen können beliebig
multiplikativ, additiv oder zurückgekoppelt vermascht sein. Jede Gleichung eines
Gesamtsystems wird hintereinander berechnet. Bei Reihenschaltungen von
Teilsystemen ist die berechnete Ausgangsgröße
die Eingangsgröße
des folgenden Teilsystems. Bei Parallelschaltungen von Teilsystemen werden die
Ergebnisse der Ausgangsgrößen additiv zusammengeführt.
Bestimmung der Differenzengleichungen aus der Regler-Übertragungsfunktion G(s)
Die Übertragungsfunktionen
der Regler und die zugehörigen elementaren Differenzengleichungen können direkt
zugeordnet werden. Die Übertragungsfunktionen eines Reglers können in der
Reihen- und Paralleldarstellung definiert werden. Dies gilt auch für die
zugehörigen Differenzengleichungen in Operatorendarstellung
.
Diese unterschiedlichen Gleichungen zur Berechnung der Regler-Ausgangsgröße für
je im s-Bereich Y(s) und je im zeitdiskreten Bereich
sind mathematisch identisch.
Gewählt wurde die Umsetzung der Übertragungsfunktion in Operatorendarstellung
der Reihendarstellung des Regelalgorithmus der Elementarsysteme, weil die
Reihendarstellung der PI- und PID-Regler je PD1-Glieder enthalten. Für den
Reglerentwurf vereinfacht sich die Parameterbestimmung, weil die PD1-Glieder des
Reglers die Verzögerungen von PT1-Gliedern der Regelstrecke bei gleichen
Zeitkonstanten direkt kompensieren können und damit die Regelstrecke
vereinfachen.
PI- und PID-Regler werden mit mehreren elementaren Differenzengleichungen im Zähler und Nenner beschrieben. Deshalb ist es nicht möglich, bei der Umsetzung vom s-Bereich in den zeitdiskreten Bereich die Differenzengleichungen mit einer Gleichung zu beschreiben. Diese Differenzengleichungen werden hintereinander berechnet. Es ist zu beachten, dass in der Reihendarstellung der Differenzengleichungen die Ausgangsgröße der ersten Differenzengleichung die Eingangsgröße der nächsten Differenzengleichung ist.
Definiert man im s-Bereich einen PID-Regler mit den Parametern
und
der Paralleldarstellung, erhält man eine Summengleichung der
Übertragungsfunktion. Wird diese Gleichung in einen gemeinsamen Zähler (s) und
Nenner (s) umgeformt, entsteht die Polynomdarstellung der Übertragungsfunktion.
Mit der Nullstellenbestimmung im Zähler und Nenner kann diese Gleichung in die
Produktdarstellung überführt werden und erkennbar wird eine Übertragungsfunktion
mit zwei PD1-Gliedern und einem I-Glied. Bedeutsam dabei ist, dass die Parameter
und
verschwunden sind und die Zeitkonstanten der beiden PD-Glieder durch andere
z.B.
und
bestimmt werden.
Für die Praxis der PID-Reglerauslegung eignet sich besser die
Übertragungsfunktion des PI-Reglers der Reihendarstellung, dem multiplikativ ein
weiteres PD-Glied mit der Zeitkonstante
zugeordnet wird. Damit werden komplizierte Umrechnungen der Parameter vermieden.
Die den Komponenten der Übertragungsfunktion G(s) zugehörigen Differenzengleichungen werden in der nachfolgenden Tabelle dargestellt.
Die bisherigen Signalbezeichnungen mit der Eingangsgröße
und der Ausgangsgröße
entsprechen den gebräuchlichen Bezeichnungen der Systemtheorie. Für den Regler
gilt das Eingangssignal bei Differenzengleichungen
und das Ausgangssignale
.
Die Reglerausgangsgröße nach der D/A-Schnittstelle lautet für das gestufte
quasikontinuierliche Signal
.
Die Verstärkungsfaktoren
der Reglerkomponenten der Differenzengleichungen werden bei einem I-Glied wie
folgt berücksichtigt:
Anmerkung: Der Quotient
entspricht bereits einem Verstärkungsfaktor.
Der Verstärkungsfaktor
der Reglerkomponenten der Differenzengleichungen wird bei einem PD-Glied wie
folgt berücksichtigt:
Differenzengleichungen der Standardregler
Tabelle der Differenzengleichungen der Standardregler (Euler-Rückwärts)
-
Regler-Typ
und TestsignaleÜbertragungsfunktion Differenzengleichung Testsignal
Impulsfunktion
U(s) = 1Amplitude:
Amplitude:Testsignal
SprungfunktionU(s) = 1 / s Testsignal
AnstiegsfunktionU(s) = 1 / s²
Anstiegskonstante c = Δ u / Δ tRegelabweichung P-Regler I-Regler PI-Regler
Parallelstruktur
PI-Regler
ReihenstrukturDarstellung der Regler-Reihenstruktur: PD1-Regler PID-Regler
Parallelstruktur
PID-Regler
ReihenstrukturDarstellung der Regler-Reihenstruktur:
= Nachstellzeit,
= Vorhaltezeit,
= P-Verstärkung,
= Diskrete Zeit bzw. Abtastzeit.
Weitere Vertiefung zu Differenzengleichung siehe Artikel Differenzengleichung
Differenzengleichungen als Funktion der Ober- und Untersumme
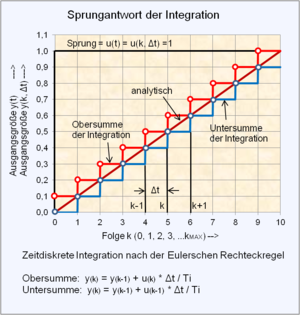
In der numerischen Mathematik bedeuten die Flächen der Rechteckapproximation an eine gegebene analytische Funktion dann als Obersumme, wenn die Oberkante der Rechtecke oberhalb der analytischen Funktion anstößt. Umgekehrt handelt es sich um die Untersumme, wenn die Oberkante der Rechtecke unterhalb der analytischen Funktion anstößt. Für die numerische Berechnung interessiert nicht die Fläche der Rechtecke, sondern die Lage des Verlaufs der Oberkante der Rechtapproximation.
Die mit Differenzengleichungen berechneten Folgeglieder der Ausgangsfolge
lassen sich als Funktion der Obersumme und Untersumme definieren. Die Ergebnisse
von Differenzengleichungen sind Folgeglieder der Wertefolge im zeitlichen
Abstand
und damit Berechnungspunkte einer Funktion, bedeuten aber keinen geschlossenen
Funktionsverlauf. Erst bei einem Digitalregler, bei dem je ein Folgeglied der
Ausgangsfolge über einen A/D-Wandler in ein Halteglied nullter Ordnung für den
Zeitraum
einfließt, wobei das Halteglied mit jedem Schritt gelöscht wird, entsteht ein
geschlossener Funktionsverlauf.
Der Funktionsunterschied der Obersumme zur Untersumme bedeutet
beispielsweise, dass ein Eingangssignal als einzelner -Impuls
zum Zeitpunkt
und Folge
in einem zeitdiskreten dynamischen System für den Zeitraum
– also zwischen
und
– wirksam wird. Differenzengleichungen nach der Untersumme können diesen
-Impuls
nicht erfassen.
Die Wertefolge der mit Differenzengleichungen berechneten Ausgangsfolge der Funktion der Untersumme unterscheiden sich von denen der Obersumme, dass die Wertefolge der Untersumme um einen Folgeschritt verzögert ist.
Grundlagen der digitalen Regler mit Hilfe der z-Transformation (Online Prozess)
Die Schnittstellen des Digitalreglers einschließlich der Abtastung mit der Haltestufe sind identisch mit dem oben aufgeführten Verfahren.
Die z-Transformation ist aus der Laplace-Transformation entstanden, um für die digitale Systemberechnung Abtastfolgen zu transformieren und damit berechenbar zu machen. Die z-Transformation ist eine Transformation von Abtastfolgen, die ähnliche Eigenschaften aufweist wie die Laplace-Transformation zur Behandlung von Differenzialgleichungen. Mit den Methoden der z-Transformation lassen sich Differenzengleichungen von abgetasteten Signalfolgen ermitteln.
Der digitale Regler wirkt in Verbindung mit den Schnittstellen zu einer meist kontinuierlich wirkenden (analogen) Regelstrecke als Computerprogramm, das die Stellgröße fortlaufend im Abstand der Abtastzeit TA die Stellgröße für die Regelstrecke berechnet. Der Regleralgorithmus ist mit der Abtastfolge und Reglerfunktion als z-Übertragungsfunktion festgelegt.
Es handelt sich bei der Gewinnung des Regelalgorithmus mit Hilfe der
z-Übertragungsfunktionen um ein völlig anderes Berechnungsverfahren, als das der
Rechteck-Approximation nach Euler-Rückwärts zur Erstellung von
Differenzengleichungen. In der z-Übertragungsfunktion wird das diskrete
abtastspezifische Zeitverhalten einer Abtastfolge wie Haltefunktionen,
D/A-Wandlung, A/D-Wandlung und Rechenzeit mit dem gewünschten Regelalgorithmus
zusammengefasst. Die inverse z-Transformation der z-Übertragungsfunktion ergibt
die benötigte Differenzengleichung .
Entsprechend den Eigenschaften der z-Transformation
ergeben sich folgende Operationen:
- Spezielle Rechenoperationen:
- Rechtsverschiebung, Linksverschiebung, Differenzensatz, Summensatz usw., zurückliegende Berechnungsfolgen sind zu speichern.
- Überführung des dynamischen Systems als z-Übertragungsfunktion,
- Eigenschaften des z-Bildbereichs ähnlich der Laplace-Transformation:
- z-Blockdarstellung von reihen- und parallelgeschalteten Systemen,
Pol-Nullstellenzerlegung, Stabilitätsbetrachtung, Berechnungsregeln und die
Überführung vom z-Bildbereich in den diskreten Zeitbereich
.
Die prinzipielle Anwendung der z-Transformation für den Regelalgorithmus lautet wie folgt:
- Die Abtastfolgen mit Haltestufe des Eingangssignals werden transformiert
als z-Übertragungsfunktion
,
- Die Differenzengleichung
des gewünschten Reglerverhaltens wird transformiert als z-Übertragungsfunktion
,
- Die z-transformierten Systeme werden algebraisch entsprechend den z-Rechenregeln zusammengefasst,
- Mit der inversen z-Transformation des z-Produktes von Signal und Regelalgorithmus entsteht der Berechnungsalgorithmus des digitalen Reglers.
Die Analyse und die Synthese diskreter Signale und Systeme lässt sich mit der z-Transformation erleichtern, setzt aber auch umfangreiches mathematisches Spezialwissen voraus, dass zum Teil auf ähnliche Regeln wie bei der Laplace-Transformation aufgebaut ist.
Siehe
auch z-Transformation
Strategie der Reglerparametrierung
Tabelle der Entwurfsstrategie von Regelkreisen bei Anwendung der Standardregler
| Funktion | Ausführung |
|---|---|
| Identifikation der Regelstrecke Siehe Artikel Regelstrecke |
|
| Pol-Nullstellen-Kompensation |
|
| P- und PD-Regler |
|
| Regler ohne statische Regelabweichung: |
|
| Regelstrecken mit Totzeit | Regelstrecken mit nennenswertem Anteil der Totzeit erfordern einen PI-Regler oder im Extremfall einen I-Regler. |
| Einstellung der P-Verstärkung | Die P-Verstärkung des Regelkreises mit dem Faktor K kann durch Simulation mit dem gewählten Regler und dem zu erfassendem Modell der Regelstrecke in einem Personal-Computer gemäß den gewünschten Kenngrößen der Übergangsfunktion (Sprungantwort) der Regelgröße eines gedämpft schwingenden Systems bestimmt werden. |
| Digitale Regler bei schnellen Regelstrecken: | Bei der Simulation eines Regelkreises mit digitalen Reglern ist das Totzeitverhalten der Schnittstellen des Mikrocomputers zu berücksichtigen, das der Regelstrecke zugeordnet werden kann. |
Tabellarische Gegenüberstellung der Verfahren der numerischen Berechnung im Offline- und Online-Prozess
Mit diesen Angaben zeigt sich ein wesentlicher Unterschied zwischen dem Offline-Prozess und dem Online-Prozess. Die Offline-Berechnung eines dynamischen Systems beziehungsweise eines aus Regler und Regelstrecke bestehenden Regelkreises hat kein Zeitverhalten, sie könnte auch mit einem Taschenrechner ohne Beeinträchtigung der Genauigkeit durchgeführt werden. Für die Offline-Berechnung (Simulation) eines realen Regelkreises mit einem Digitalregler muss das Zeitverhalten der Schnittstellen des Digitalreglers als Totzeit berücksichtigt werden.
Die Online-Berechnung des Digitalreglers hat innerhalb jeder Abtastfolge
Totzeiten, die sich durch die erforderlichen Schnittstellen der Signalwandlung
im Eingang und Ausgang, im Halteglied sowie durch die Rechenzeit der Berechnung
der Differenzengleichungen ergeben. Soweit es sich um die Regelung schneller
Regelstrecken (z.B. Dominante Zeitkonstante
= 1 s der Regelstrecke) handelt, sind schnelle Komponenten der Wandler und des
Mikrocomputers
erforderlich, um die Ersatztotzeit im Verhältnis zur dominanten Zeitkonstante
der Regelstrecke und zur Abtastzeit klein zu halten.
| Numerische Berechnung dynamischer Systeme
(Offline-Prozess) (Differenzengleichungen nach dem Euler-Rückwärtsverfahren) |
Regelung mit Digitalreglern
(Online-Prozess) (Differenzengleichungen nach dem Euler-Rückwärtsverfahren) |
|---|---|
| Dynamisches System: Steuerstrecke oder Regelkreis. Gemischte lineare und nichtlineare Systeme lassen sich simulieren. |
Dynamisches System: Digitalregler wirkt auf eine analoge
Regelstrecke. Digitale Regler für beliebige Anwendungen sind möglich. |
| System-Eingangsgröße: Bei dynamischen Systemen als Testsignal u(k), Bei Regelkreisen die Führungsgröße als Testsignal w(k). |
System-Eingangsgröße: Bei Vorgabe der analogen Regelabweichung e(t) = w(t) - y(t), e(t) wird als Eingangsfolge abgetastet und digitalisiert als e(k). |
| System-Ausgangsfolge: y(k) Die Ausgangsfolge sind Zahlenwerte der Folge k. |
Reglerausgangsfolge: u(k) u(k) sind Zahlenwerte der Folge k. u(k) wird nach der D/A-Wandlung eine gestufte analoge Größe u(t) (Spannung). |
| Abtastfolge k bedeutet Nummerierung der Folgeglieder: |
Abtastfolge k bedeutet Nummerierung der Folgeglieder: |
| Diskrete Zeit |
Abtastzeit |
| Größe der diskreten Zeit Z.B. |
Größe der Abtastfolge TA: Z.B. |
| Differenzengleichungen: z.B. Methode Euler-Rückwärts vorhergehende Rechenfolge: Benötigt werden Differenzengl. der Teilsysteme von Regler und Strecke. |
Differenzengleichungen: z.B. Methode Euler-Rückwärts vorhergehende Rechenfolge: Benötigt werden die Differenzengleichungen der Teilsysteme des Digitalreglers. |
| Berechnungsvorgang: tabellarisch Den Übertragungsfunktionen 1. Ordn. sind Differenzengleichungen zugeordnet. Jede Zeile berechnet die Differenzengleichungen aller Teilsysteme. Es existieren kmax +1 Glieder = Zeilen = Ausgangsfolge. Nur 2 wechselnde aktuelle Glieder der Ausgangsfolge sind relevant: Sämtliche Zeilen werden als Protokoll gespeichert. |
Berechnungsvorgang: kontinuierlich Die Abtastfolge startet im zeitlichen Abstand TA die Berechnung der Teilsysteme des Digitalreglers mit den zugehörigen Differenzengleichungen. Nur 2 wechselnde aktuelle Glieder der Ausgangsfolge sind relevant: Jedes Glied der Ausgangsfolge wird zu einer quasi analogen Stellgröße f(t) verarbeitet. |
| Schnittstellen: keine Eingangssignal Ausgangssignal |
Schnittstellen: für analoge Regelabweichung Im Eingang: AD-Wandler (kurze Halteglied-Funktion) für Berechnungsdauer, Im Ausgang: DA-Wandler mit Halteglied für gestufte analoge Stellgröße |
| Totzeit der numerischen Berechnung: keine durch das Verfahren bedingt, (Gilt für Euler-Rückwärts-Verfahren der Obersumme) Das Totzeitverhalten der Regelstrecke kann nachgebildet werden. |
Totzeit des Digitalreglers:
|
| Numerische Stabilität:
Bedingung zur Vermeidung der numerischen Instabilität: |
Numerische Stabilität: Wegen der unvermeidlichen Totzeiten ist eine hohe P-Verstärkung nicht möglich. |
| Genauigkeit der numerische Simulation: Die Genauigkeit steigt mit kleiner werdendem Zeitintervall Der Approximationsfehler |
Genauigkeit der numerischen Berechnung: Die Genauigkeit steigt mit kleiner werdender Abtastzeit Sonst wie Offline-Prozess. |
| Ideale und reale Regler der Regelkreisnachbildung: Sie sind identisch. |
Reale Digitalregler: Es ist nicht möglich, ohne Zeitverzögerung einen Rechenwert u(t) in eine Stellgrößenenergie umzusetzen. |
Literatur
- Gerd Schulz: Regelungstechnik 2 / Mehrgrößenregelung, Digitale Regelungstechnik, Fuzzy-Regelung. 2. Auflage. Oldenbourg, 2008, ISBN 978-3-486-58318-2.
- Jan Lunze: Regelungstechnik 2, Mehrgrößensysteme, Digitale Regelung. 7. Auflage. Springer Verlag, 2013, ISBN 978-3-642-10197-7.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 08.12. 2025