Stetigkeit (Topologie)
In der Topologie bezeichnet man Funktionen oder Abbildungen als stetig, wenn diese bestimmte Morphismen zwischen topologischen Räumen sind, die die topologische Struktur in einem gewissen Sinne erhalten. Deshalb sind sie auch von besonderem Interesse. Die Definitionen von Stetigkeit in anderen Teilgebieten der Mathematik leiten sich aus der Definition in der Topologie ab. Die Stetigkeit ist grundlegend für den in der Topologie wichtigen Begriff des Homöomorphismus: eine bijektive stetige Funktion ist genau dann homöomorph, wenn auch ihre Umkehrfunktion stetig ist.
Nicht stetige Funktionen oder Abbildungen heißen unstetig.
Eng verwandt mit dem Begriff der Stetigkeit sind die Begriffe der gleichmäßigen Stetigkeit, der gleichgradigen Stetigkeit und auch der Begriff der Beschränktheit linearer Operatoren.
Definitionen
Da man topologische Räume auf unterschiedliche (aber äquivalente) Weise definieren kann, existieren auch mehrere gleichwertige Definitionen der Stetigkeit. Im Folgenden finden sich bei jeder Definition mehrere Varianten, die sich durch ihren Grad an Formalisierung unterscheiden.
Offene Mengen
- Eine Funktion zwischen zwei topologischen Räumen ist genau dann stetig, wenn die Urbilder offener Mengen wiederum offene Mengen sind.
- Sei f eine Abbildung von dem topologischen Raum X in den topologischen Raum Y. Dann heißt f stetig, wenn das Urbild unter f von jeder in Y offenen Menge O wieder offen in X ist.
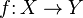 stetig
stetig 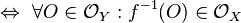 (wobei
(wobei 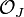 die Topologie des Raumes J, also die Menge der offenen Mengen des
topologischen Raumes ist)
die Topologie des Raumes J, also die Menge der offenen Mengen des
topologischen Raumes ist)
Abgeschlossene Mengen
Die Stetigkeit kann durch abgeschlossene Mengen definiert werden, indem man „offene Mengen“ in obiger Definition durch „abgeschlossene Mengen“ ersetzt:
- Eine Funktion zwischen zwei topologischen Räumen ist genau dann stetig, wenn die Urbilder abgeschlossener Mengen wiederum abgeschlossene Mengen sind.
- Sei f eine Abbildung von dem topologischen Raum X in den topologischen Raum Y. Dann heißt f stetig, wenn das Urbild unter f von jeder in Y abgeschlossene Menge A wieder abgeschlossen in X ist.
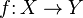 stetig
stetig 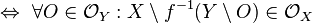
Umgebungen
Sei 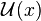 die Menge aller Umgebungen eines Punktes x.
die Menge aller Umgebungen eines Punktes x.
- Eine Funktion zwischen zwei topologischen Räumen ist genau dann stetig, wenn für jeden Punkt gilt: für jede Umgebung des Bildpunktes dieses Punktes gibt es eine Umgebung des Punktes, deren Bild komplett in der Umgebung des Bildpunktes liegt.
- Sei f eine Abbildung
von dem topologischen Raum X in den topologischen Raum Y. Dann
ist f genau dann stetig, wenn für jeden Punkt x in X
gilt: Ist U eine Umgebung von
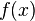 ,
dann gibt es eine Umgebung V von x, so dass
,
dann gibt es eine Umgebung V von x, so dass 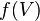 in U enthalten ist.
in U enthalten ist. 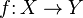 stetig
stetig 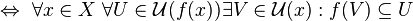
Netze
Für eine gerichtete
Menge 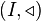 und eine Menge
und eine Menge 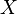 ist ein Netz
eine Abbildung
ist ein Netz
eine Abbildung
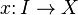 .
Meist schreibt man analog zu Folgen
.
Meist schreibt man analog zu Folgen
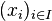 .
Da die natürlichen
Zahlen mit der gewöhnlichen Anordnung eine gerichtete Menge bilden, sind
Folgen spezielle Netze.
.
Da die natürlichen
Zahlen mit der gewöhnlichen Anordnung eine gerichtete Menge bilden, sind
Folgen spezielle Netze.
- Seien X und Y topologische Räume. Eine Abbildung
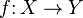 ist genau dann stetig, wenn für alle
ist genau dann stetig, wenn für alle 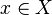 gilt: Für jedes in X gegen
gilt: Für jedes in X gegen 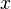 konvergente
Netz
konvergente
Netz 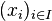 konvergiert das Netz
konvergiert das Netz 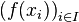 in Y gegen
in Y gegen 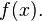
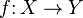 stetig
stetig 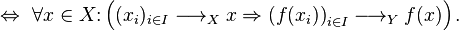
Abschluss
- Eine Funktion zwischen zwei topologischen Räumen ist genau dann stetig, wenn das Bild des Abschlusses einer beliebigen Teilmenge im Abschluss des Bildes dieser Teilmenge enthalten ist.
- Sei f eine Abbildung von dem topologischen Raum X in den topologischen Raum Y. Dann ist f genau dann stetig, wenn für jede Teilmenge A von X gilt: das Bild des Abschlusses von A liegt im Abschluss des Bildes von A.
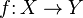 stetig
stetig 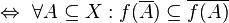
Eigenschaften von stetigen Funktionen
- Wenn
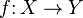 und
und 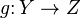 stetige Funktionen sind, dann ist die Komposition
stetige Funktionen sind, dann ist die Komposition
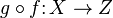 auch stetig.
auch stetig. - Wenn
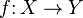 stetig und
stetig und
- X kompakt
ist, dann ist
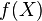 kompakt.
kompakt. - X zusammenhängend
ist, dann ist
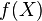 zusammenhängend.
zusammenhängend. - X wegzusammenhängend
ist, dann ist
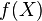 wegzusammenhängend.
wegzusammenhängend.
- X kompakt
ist, dann ist
Anmerkungen
- Für eine Definitionsmenge
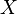 mit der diskreten
Topologie ist jede Funktion
mit der diskreten
Topologie ist jede Funktion 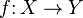 in einen beliebigen Raum
in einen beliebigen Raum 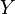 stetig.
stetig. - Für eine Zielmenge
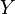 mit der indiskreten
Topologie ist jede Funktion
mit der indiskreten
Topologie ist jede Funktion 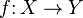 in diesen Raum
in diesen Raum 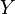 stetig.
stetig. - Für eine Definitionsmenge mit der indiskreten Topologie und eine Zielmenge, die ein T0-Raum ist, sind die konstanten Funktionen die einzigen stetigen Funktion.
- Stetigkeit ist eine lokale Eigenschaft.
Betrachtet man bei einer Funktion nicht wie bei der Stetigkeit die Urbilder, sondern die Bilder der Funktion, so gelangt man zu den Begriffen der offenen bzw. abgeschlossenen Abbildung.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 02.09. 2019