
Glatter Raum
Glatte normierte Räume werden im mathematischen Teilgebiet der Funktionalanalysis untersucht. Es handelt sich um normierte Räume, deren Norm eine gewisse Glattheitseigenschaft hat.
Definitionen
Es sei
ein normierter Raum,
sei die Einheitskugel
und
ihr Rand,
die sogenannte Einheitssphäre.
Nach dem Satz
von Hahn-Banach gibt es zu jedem
ein stetiges,
lineares
Funktional
mit
und
.
Dieses Funktional
definiert die Hyperebene
,
die
in
schneidet und keinen Punkt aus dem Inneren
der Einheitskugel enthält. Eine solche Hyperebene nennt man eine
Stützhyperebene an
,
das Funktional
heißt Stützfunktional an
.
Stellt man sich eine Hyperebene als lineare
Approximation der Kugeloberfläche vor, so liegt es nahe, einen Punkt
einen Glattheitspunkt zu nennen, wenn es genau eine Stützhyperebene an
gibt, das heißt, wenn es genau ein
gibt mit
und
.
Ein normierter Raum heißt glatt, wenn jeder Punkt der Einheitssphäre ein Glattheitspunkt ist. Die Einheitskugel eines glatten Raums ist damit eine glatte konvexe Menge.
Stützabbildung
Man nennt eine Abbildung ,
eine Stützabbildung, falls folgendes gilt:
- Aus
folgt
- Für
und
gilt
.
Definitionsgemäß gibt es in einem glatten Raum genau eine Stützabbildung, man
kann also von der Stützabbildung eines glatten Raums sprechen. Man kann
zeigen, dass diese norm-schwach*-stetig ist, das heißt stetig, wenn man auf
die Normtopologie und auf
die schwach-*-Topologie
betrachtet.
Beispiele
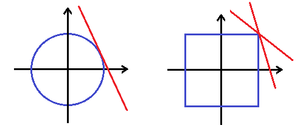
Zweidimensionaler Raum
Glattheit hängt von der Norm ab und kann beim Übergang zu einer äquivalenten
Norm verloren gehen. Das zeigt sich schon am Beispiel des zweidimensionalen
Raums .
Versieht man den zweidimensionalen Raum mit der euklidischen Norm
,
so ist die Einheitssphäre ein Kreis
und jeder Punkt hat genau eine Stützhyperebene, nämlich die Tangente an diesem Punkt, das
heißt
ist glatt. Betrachtet man auf dem
die Maximumsnorm
,
so ist die „Einheitskugel“ ein Quadrat.
An jeder Ecke des Quadrates gibt es unendlich viele Stützhyperebenen, alle
anderen Punkte sind Glattheitspunkte. Damit ein Raum glatt ist, muss aber jeder
Punkt der Einheitssphäre ein Glattheitspunkt sein, das heißt
ist nicht glatt. Da die euklidische Norm und die Maximumsnorm auf dem
äquivalent sind, sieht man an diesem Beispiel, dass die Glattheit beim Übergang
zu einer äquivalenten Norm verloren gehen kann.
Weitere Beispiele
- Hilberträume sind glatt,
die Stützabbildung lautet
.
- Die Lp[0,1]-Räume und
die Folgenräume
sind für
glatt. Allgemeiner sind gleichmäßig glatte Räume glatt.
- Ist
ein kompakter Hausdorffraum mit mindestens zwei Punkten, so ist der Funktionenraum
der stetigen Funktionen auf
mit der Supremumsnorm nicht glatt.
Charakterisierungen
Folgende Aussage über einen normierten Raum
sind äquivalent:
ist glatt.
- Die Norm auf
ist Gâteaux-differenzierbar, das heißt für jedes
und
existiert
.
- Jede Stützabbildung des Raums ist norm-schwach*-stetig.
- Es gibt eine norm-schwach*-stetige Stützabbildung.
- Für jedes
und jede Folge
in
mit
folgt, dass
schwach*-konvergiert.
- Jeder zwei-dimensionale Unterraum ist glatt.
- Die Orthogonalität
ist rechts-additiv, das heißt aus
und
folgt
.
Dualität
Über die Dualität besteht ein enger Zusammenhang zur strikten Konvexität.
- Ein normierter Raum
ist glatt, falls sein Dualraum strikt konvex ist.
- Ein normierter Raum
ist strikt konvex, falls sein Dualraum glatt ist.
Die Umkehrungen gelten im Allgemeinen nicht.
Renormierbarkeit
Da die Glattheit beim Übergang zu einer äquivalenten Norm verloren gehen kann, stellt sich in natürlicher Weise die Frage, zu welchen normierten Räumen es äquivalente, glatte Normen gibt, die also durch Übergang zu einer äquivalenten Norm glatt werden. Solche Räume nennt man glatt renormierbar.
Reflexive Räume sind strikt konvex renormierbar und daher wegen obiger Dualitätseigenschaften auch glatt renormierbar, sogar glatt und gleichzeitig strikt konvex renormierbar. Das gilt allgemeiner für schwach kompakt erzeugte Räume.
ist nicht glatt renormierbar.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 07.12. 2020