
Durchbiegung
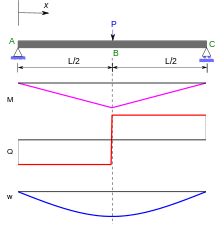
Als Durchbiegung länglicher Gegenstände wie Balken oder Stäben wird der Versatz zwischen belasteter und unbelasteter Lage bezeichnet, der bei Biegebelastung quer zur Längsachse entsteht.
Die Durchbiegung lässt sich bei linear-elastischer
Verformung mit Hilfe der Balkentheorie berechnen.
Als Durchbiegung wird i.d.R. der Versatz
bezeichnet, der in der dabei ermittelten Biegelinie
an einer Stelle
dargestellt wird.
Durchbiegung von Balken
Die erste Biegetheorie stammt von Galilei (1564–1642). Weiter ausgebaut wurde sie v.a. durch das Hookesche Gesetz (1678) sowie im 17. und 18. Jahrhundert durch Forschungen von Jakob I Bernoulli, Leonhard Euler und Claude Navier
Unter der Annahme, dass y und z die Hauptträgheitsachsen
sind (y horizontal nach hinten und z vertikal) und dass sich die Krümmung
in y-Richtung, d.h. die Ableitung des Steigungswinkels w'
in der vertikalen xz-Bildebene, an der Stelle x wie folgt berechnen
lässt:
,
gilt:
mit
- Krümmung
aufgrund von Biegung (unter Annahme der Balkentheorie)
- Biegemoment My quer zur Stabrichtung, an der Stelle x
- Biegesteifigkeit
- Elastizitätsmodul E (ein Materialkennwert) (im inelastischen (z.B. Beton) oder nichtlinearen Bereich (z.B. Elastomerlager) ist dieser mit einem geeigneten Sekantenmodul zu ersetzen)
- Flächenträgheitsmoment I des Balkenquerschnitts (eine rein geometrische Eigenschaft)
- eingeprägter Krümmung
(z.B. zufolge Temperaturdifferenz)
- Schubdeformation
zufolge Querkraft
- Schubsteifigkeit
- Schubmodul
- Balken-Querschnittsfläche
in der yz-Ebene.
- Schubmodul
- Schubsteifigkeit
Für die Biegelinie eines hinreichend elastischen, schlanken Bauteiles mit
konstantem Querschnitt lautet eine oft verwendete Näherungsformel
der Krümmung für betragsmäßig kleine Steigungswinkel w'≈0 unter
ausschließlicher Momentenbelastung ():
Die eigentlich gesuchte Durchbiegung w erhält man durch
zweimalige Integration
der Krümmung unter Berücksichtigung der Rand- und
Übergangsbedingungen (u.a.: keine Durchbiegung an den Lagerstellen, d.h. ):
Beispiele
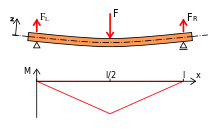
1. Beispiel
Wirkt die Kraft F mittig
(d.h. bei der halben Stablänge )
auf einen Träger
mit konstanten Querschnittseigenschaften auf zwei Stützen, so ist das
Biegemoment und damit auch die Stabkrümmung in der Stabmitte am größten
(Erläuterung hier):
Für
gilt unter Vernachlässigung der Schubverformungen (GA=∞):
damit folgt unter Berücksichtigung der Randbedingung
und der Übergangsbedingung
:
und somit:
2. Beispiel
Wirkt eine konstante Liniengleichlast
(
in N/m)
auf einen Träger auf zwei Stützen mit konstanten Querschnittseigenschaften, so
gilt unter Vernachlässigung der Schubverformungen (GA=∞):
Dies ergibt:
Anmerkung:
Bei Linienlast
ist Ausgangsgleichung die 4. Ableitung der Biegelinie:
Diese (mit )
wurde viermal integriert, wobei nach dem zweiten Integrieren als
Zwischenergebnis der Zusammenhang zwischen der Biegelinie und dem
Biegemomentverlauf gefunden wurde:
Durchbiegung von Kreisflächen
Bei flächenhafter Ausdehnung des Gegenstandes wird die Berechnung recht kompliziert, lässt sich aber bei Kreisflächen – etwa für Membranen (z.B. Lautsprecher) oder große Linsen (z.B. Fernrohrobjektive) – ebenfalls abschätzen.
Hat die Membran eine nur geringfügige Dicke d, so folgen die Biegemomente einer radialen bzw. tangentialen Differentialgleichung. Die Biegelinie der Kreismembran erfordert aber eine zusammengesetzte Differentialformel, die bei einer Querkraft Q genähert lautet:
mit
- Widerstandsmoment
- Poissonzahl ν des Materials.
Komplexere Fälle
Solange ein Gegenstand sich auf einer Ebene mit Querschnittseigenschaften/Plattenerzeugendeneingenschaften eindeutig abbildbar und homogen, orthotrop und linear elastisch aufgebaut ist, bietet die analytische Mechanik Lösungsmöglichkeiten auch für andere regelmäßige Formen (Airy’sche Spannungsfunktion). Auch Fälle mit unterschiedlichen Materialien sind genähert lösbar, wenn ihre Verbindungsstellen mechanisch klar definiert sind, z.B. bei axialer Anordnung.
Komplexere Formen sind jedoch nicht streng berechenbar. Sie werden oftmals durch Biegeversuche im Labor oder mathematisch-physikalisch durch Zerlegung in netzartige Teile (v.a. Finite-Elemente-Methoden) untersucht. Für Beton gibt es für die Baupraxis ausreichend genaue Annahmen, um es im ungerissenen Bereich (der Mikrorisse, jedoch keine Makrorisse enthält) als verschmiert homogenes Material betrachten zu können.
Literatur
- Heinz Parkus: Mechanik der festen Körper, 2. Auflage. Springer-Verlag, Wien 1966, ISBN 3-211-80777-2
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 29.12. 2021