Lokal zusammenhängend

Lokal zusammenhängende Räume werden im mathematischen Teilgebiet der Topologie betrachtet. Es handelt sich um topologische Räume, die um jeden Punkt herum im Kleinen zusammenhängend sind.

Definitionen

Ein topologischer Raum heißt lokal zusammenhängend im Punkt $x\in X$ , wenn eine Umgebungsbasis aus offenen und zusammenhängenden Mengen besitzt.
Ein topologischer Raum heißt lokal zusammenhängend, wenn er in jedem seiner Punkte lokal zusammenhängend ist.

Indem man die Definition der Umgebungsbasis in obige Definition einbaut, kann man dies auch wie folgt umformulieren:

Ein topologischer Raum heißt lokal zusammenhängend, falls es zu jedem $x\in X$ und jeder offenen Menge $U\subset X$ mit $x\in U$ eine offene und zusammenhängende Menge gibt mit $x\in V\subset U$ .

Beispiele

Jede offene Menge $U\subset \mathbb {R} ^{n}$ ist mit ihrer Teilraumtopologie lokal zusammenhängend, denn zu jedem $x\in U$ bilden die vollständig in gelegenen Kugeln um eine Umgebungsbasis der verlangten Art.
Die Vereinigung zweier oder mehrerer disjunkter, nicht-leerer Mengen im $\mathbb {R} ^{n}$ zeigt, dass lokal zusammenhängende Räume im Allgemeinen nicht zusammenhängend sind.
Das Einheitsintervall, das Einheitsquadrat, allgemeiner Quader im $\mathbb {R} ^{n}$ sind lokal zusammenhängend.
Diskrete Räume und Räume mit der trivialen Topologie sind lokal zusammenhängend. Im ersten Fall ist jede einpunktige Menge eine Umgebungsbasis des enthaltenen Punktes, im zweiten Fall ist der Gesamtraum eine Umgebungsbasis.

Topologischer Kamm

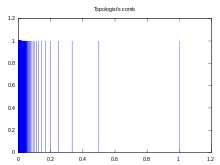
Der topologische Kamm $K=(\{{\tfrac {1}{n}}|n\in \mathbb {N} \}\times [0,1])\cup ([0,1]\times \{0\})\cup (\{0\}\times [0,1])\subseteq \mathbb {R} ^{2}$ ist in den Punkten aus $\{0\}\times (0,1]$ nicht lokal zusammenhängend, da hinreichend kleine Kugeln um diese Punkte stets aus unendlich vielen unzusammenhängenden Strecken bestehen. Da dieser Raum zusammenhängend ist, zeigt dieses Beispiel, dass zusammenhängende Räume im Allgemeinen nicht lokal zusammenhängend sind.
Der Raum $\mathbb {Q}$ mit der Teilraumtopologie von $\mathbb {R}$ ist in keinem Punkt lokal zusammenhängend.
Jeder topologische Raum $(X,\tau )$ besitzt eine gröbste lokal zusammenhängende Topologie $\tau_0$ , die feiner als $\tau$ ist, nämlich

$\tau _{0}=\bigcap \left\{\sigma \mid \sigma {\text{ ist lokal zusammenhängende Topologie auf }}X{\text{ mit }}\sigma \supset \tau \right\}$

Es ist klar, dass die diskrete Topologie stets in der Menge, über die der Durchschnitt gebildet wird, enthalten ist. Man zeigt dann, dass dieser Durchschnitt eine lokal zusammenhängende Topologie auf ist.

Der Übergang von einem topologischen Raum zu dem so konstruierten lokal zusammenhängenden Raum ist ein Funktor, der rechtsadjungiert zum Vergissfunktor ist, der den lokalen Zusammenhang vergisst. Die Kategorie der lokal zusammenhängenden Räume ist demnach eine koreflektive Unterkategorie in der Kategorie der topologischen Räume.

Äquivalente Charakterisierungen

Ein topologischer Raum ist genau dann lokal zusammenhängend, wenn jede Zusammenhangskomponente jeder offenen Menge offen ist.
Ein topologischer Raum ist genau dann lokal zusammenhängend, wenn die offenen und zusammenhängenden Mengen eine Basis der Topologie bilden.

Eigenschaften

Offene Unterräume lokal zusammenhängender Räume sind wieder lokal zusammenhängend, wie sich unmittelbar aus der Definition ergibt. Beliebige Unterräume sind im Allgemeinen nicht wieder lokal zusammenhängend. So ist obiges Beispiel des topologischen Kamms ein abgeschlossener Unterraum des lokal zusammenhängenden Einheitquadrats $[0,1]\times [0,1]$ .
Quotientenräume lokal zusammenhängender Räume sind wieder lokal zusammenhängend.

Im Allgemeinen sind stetige Bilder lokal zusammenhängender Räume nicht wieder lokal zusammenhängend. Es gilt aber:

Ist $f\colon X\rightarrow Y$ eine stetige, surjektive Abbildung eines kompakten, lokal zusammenhängenden Raums auf einen Hausdorffraum , so ist lokal zusammenhängend.

Endliche Produkte lokal zusammenhängender Räume sind wieder lokal zusammenhängend. Für beliebige Produkte ist das im Allgemeinen falsch. Hier gilt:

Ist $(X_{i})_{i\in I}$ eine Familie lokal zusammenhängender Räume, so ist das Produkt $\textstyle \prod _{{i\in I}}X_{i}$ genau dann lokal zusammenhängend, wenn alle $X_{i}$ bis auf höchstens endliche viele Ausnahmen zusammenhängend sind.

Die Kategorie der lokal zusammenhängenden Räume ist eine Kategorie mit beliebigen Produkten. Das Produkt einer Familie $(X_{i})_{i\in I}$ in der Kategorie der lokal zusammenhängenden Räume ist das kartesische Produkt versehen mit der gröbsten lokal zusammenhängenden Topologie, die feiner als die Produkttopologie ist.

Satz von Hahn-Mazurkiewicz

Der Satz von Hahn-Mazurkiewicz, benannt nach Hans Hahn und Stefan Mazurkiewicz, charakterisiert diejenigen Hausdorffräume, die Quotientenraum des Einheitsintervalls sind. Nach Obigem müssen diese lokal zusammenhängend sein, aber auch Eigenschaften wie Kompaktheit, Zusammenhang und das zweite Abzählbarkeitsaxiom folgen sofort. Die Umkehrung ist die nicht-triviale Richtung im folgenden Satz

Satz von Hahn-Mazurkiewicz: Ein Hausdorffraum ist genau Quotientenraum des Einheitsintervalls, wenn er kompakt, zusammenhängend, lokal zusammenhängend ist und eine abzählbare Basis hat.

Zusammenhängende, kompakte Hausdorffräume mit abzählbarer Basis nennt man auch Kontinua. Damit lässt sich der Satz von Hahn-Mazurkiewicz wie folgt umformulieren:

Ein Kontinuum ist genau dann Quotientenraum des Einheitsintervalls, wenn es lokal zusammenhängend ist.

Insbesondere ist eine kompakte und zusammenhängende Teilmenge des $\mathbb {R} ^{n}$ genau dann stetiges Bild des Einheitsintervalls, wenn sie lokal zusammenhängend ist.

Basierend auf einem Artikel in:

Wikipedia.de