
CAT(0)-Raum
CAT(0)-Räume sind ein Begriff aus der Geometrie, mit dem Eigenschaften von Mannigfaltigkeiten nichtpositiver Krümmung auf allgemeine metrische Räume verallgemeinert werden. Ihre definierende Eigenschaft ist, dass Dreiecke dünner sein sollen als Vergleichsdreiecke in der euklidischen Ebene.
Definition
Vergleichsdreiecke
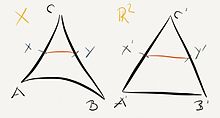
Sei
ein geodätischer
metrischer Raum. Ein geodätisches Dreieck
in
ist ein Dreieck mit Ecken
,
dessen drei Seiten Geodäten sind. Zu jedem geodätischen Dreieck
gibt es ein (bis auf Kongruenz
eindeutiges) Vergleichsdreieck
im
mit
.
Man hat dann eine Vergleichsabbildung
,
die (zum Beispiel) jedem Punkt
auf der Seite
den entsprechenden Punkt
auf der Seite
(d.h. den eindeutigen Punkt mit
)
zuordnet, analog für die beiden anderen Seiten.
CAT(0)-Räume
Ein geodätischer metrischer Raum
ist ein CAT(0)-Raum, wenn zu jedem geodätischen Dreieck
in
mit Vergleichsabbildung
die Ungleichung
für alle
gilt.
Anschaulich: Jedes geodätische Dreieck ist mindestens so dünn wie sein Vergleichsdreieck.
Beispiele
- Einfach
zusammenhängende vollständige
Riemannsche
Mannigfaltigkeiten nichtpositiver Schnittkrümmung
sind CAT(0)-Räume. Dazu zählen der euklidische
, der hyperbolische Raum,
, allgemeiner alle symmetrischen Räume ohne kompakten Faktor.
- Einfach zusammenhängende vollständige Riemannsche Mannigfaltigkeiten nichtpositiver Schnittkrümmung werden auch als Hadamard-Mannigfaltigkeiten bezeichnet. Vollständige CAT(0)-Räume bezeichnet man als Hadamard-Räume.
- Endliche Produkte von CAT(0)-Räumen sind CAT(0)-Räume.
-Bäume und euklidische oder hyperbolische Gebäude sind CAT(0)-Räume.
- Hilberträume sind CAT(0)-Räume.
- Eine zusammenziehbare
Mannigfaltigkeit der Dimension
trägt genau dann eine geodätisch vollständige CAT(0)-Metrik, wenn sie kollabierbar ist.
- Satz von Gromov: Ein kubischer Komplex ist genau dann ein CAT(0)-Raum, wenn er einfach zusammenhängend und der Link jeder Ecke ein Fahnenkomplex ist.
Eigenschaften
- In einem CAT(0)-Raum
lassen sich je zwei Punkte durch eine eindeutige Geodäte verbinden. Die Geodäte hängt stetig von ihren Endpunkten ab.
- In CAT(0)-Räumen gilt die Ptolemäische Ungleichung
für alle
.
- Für Geodäten
ist die Funktion
konvex.
- CAT(0)-Räume sind zusammenziehbar.
Geodätischer Rand
Geodätische Strahlen in einem CAT(0)-Raum heißen asymptotisch, wenn
sie endlichen Abstand haben. Dies definiert eine Äquivalenzrelation auf der
Menge der geodätischen Strahlen. Der Geodätische Rand
des CAT(0)-Raumes
ist die Menge der Äquivalenzklassen von auf Bogenlänge parametrisierten
geodätischen Strahlen.
Jeder Punkt in
lässt sich mit jedem Punkt in
durch eine eindeutige Geodäte verbinden. Unterschiedliche Punkte in
müssen sich aber nicht immer durch eine Geodäte verbinden lassen.
Kegel-Topologie
Die Topologie
auf
lässt sich zu einer Topologie auf
erweitern,
so dass gilt: Eine Folge
konvergiert gegen
genau dann, wenn (für beliebiges
)
die Folge der
und
verbindenden Geodäten lokal gleichmäßig gegen die
und
verbindende Geodäte konvergiert.
Diese Topologie wird als Kegel-Topologie bezeichnet.
Beispiel: Wenn
eine einfach zusammenhängende, vollständige n-dimensionale Riemannsche
Mannigfaltigkeit nichtpositiver Schnittkrümmung ist, dann ist
mit der Kegel-Topologie homöomorph
zur (n-1)-dimensionalen Sphäre.
Tits-Metrik
Die Tits-Metrik
ist für
definiert durch
,
wobei
zu
asymptotische Geodäten sind.
Hierbei ist (allgemein für )
der Winkel
definiert als der Winkel bei
des Vergleichsdreiecks
im
.
Die Tits-Metrik induziert im Allgemeinen nicht die Kegel-Topologie auf .
Beispiele: Falls
eine einfach zusammenhängende, vollständige Riemannsche Mannigfaltigkeit
negativer Schnittkrümmung ist, dann ist
für alle
,
die Tits-Metrik induziert also die diskrete
Topologie. Falls
der euklidische Raum ist, dann ist
homöomorph zur Sphäre.
Horosphären
Zu einem Punkt
und einer Geodäte
mit
definiert man die Busemann-Funktion
durch
.
Falls
vollständig ist und
und
zwei zu
asymptotische Geodäten sind, dann ist
konstant. Insbesondere hängt die Zerlegung von
in die Niveaumengen von
nur von
und nicht von der Wahl der zu
asymptotischen Geodäte
ab. Die Niveaumengen von
werden als Horosphären von
bezeichnet.
Isometrien
Jede Isometrie
eines vollständigen CAT(0)-Raumes
fällt in eine der folgenden 3 Klassen:
- elliptisch:
hat einen Fixpunkt in
,
- hyperbolisch:
hat keinen Fixpunkt in
, lässt aber eine Geodäte invariant,
- parabolisch:
lässt einen Punkt
und seine Horosphären invariant.
CAT(0)-Gruppen
Eine CAT(0)-Gruppe ist eine Gruppe, die eigentlich diskontinuierlich und kokompakt durch Isometrien auf einem endlich-dimensionalen CAT(0)-Raum wirkt.
Lokale CAT(0)-Räume
Ein vollständiger, zusammenhängender, metrischer Raum heißt lokal CAT(0), wenn jeder Punkt eine Umgebung besitzt, die (mit der eingeschränkten Metrik) ein CAT(0)-Raum ist.
Eine Verallgemeinerung des Satzes
von Cartan-Hadamard besagt: wenn
ein lokaler CAT(0)-Raum ist, dann gibt es auf der universellen Überlagerung
eine eindeutige Metrik
so dass
- die Überlagerung
eine lokale Isometrie ist, und
ein CAT(0)-Raum ist.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 09.10. 2020