Farbvalenz

Die Farbvalenz eines Lichtstrahls ist eine physiologische Kenngröße. Sie beschreibt die Wirkung des Lichtstrahls auf die farbempfindlichen Sinneszellen des menschlichen Auges. Im Gegensatz zur Spektralverteilung, also der vollständigen Information über die im Lichtstrahl vorhandenen Spektralfarben, beschränkt sich die Farbvalenz auf die weniger umfangreiche und durch drei Zahlenwerte darstellbare Information, welche Farbwahrnehmung der Lichtstrahl im Auge auslöst.

Die von den Farbrezeptoren des Auges erfasste Farbe hängt von der spektralen Zusammensetzung des Lichtstrahles ab. Lichtstrahlen mit gleicher spektraler Zusammensetzung lösen im Auge dieselbe Reizung der Rezeptoren aus. Da den unendlich vielen sichtbaren Wellenlängen des Lichts jedoch nur drei Arten von Farbrezeptoren des Auges gegenüberstehen, kann der Mensch nicht alle Kombinationen von Spektralfarben unterscheiden; es gibt daher Kombinationen von Spektralfarben, die voneinander verschieden sind, aber im Auge den gleichen Farbreiz und damit dieselbe Farbwahrnehmung auslösen. Allen Lichtstrahlen, die im Auge dieselbe Farbwahrnehmung erzeugen, wird dieselbe Farbvalenz zugeordnet – auch wenn sie spektral unterschiedlich zusammengesetzt sind (Metamerie). Lichtstrahlen gleicher Farbvalenz verhalten sich auch in additiven Farbmischungen gleich, haben hier also dieselbe Wertigkeit („Valenz“).

Farbvalenzen lassen sich als dreidimensionale Koordinaten bzw. Vektoren in einem Farbraum auffassen und entsprechend berechnen. Die Farbmetrik handelt von jenen Aussagen, die sich aus diesen Rechenregeln in Verbindung mit dem Gleichheits- oder Ungleichheitsurteil des Auges ableiten lassen. Insbesondere folgen daraus die Rechenregeln für die additive Farbmischung.

Die Bestimmung der Farbvalenz eines Lichtstrahls kann erfolgen durch:

unmittelbare Messung; dabei vergleicht ein Beobachter den Lichtstrahl mit einer additiven Mischung von Referenz-Farbvalenzen; die Farbempfindungseigenschaften des Beobachterauges gehen also unmittelbar in die Messung ein.
durch Rechnung; dabei wird die Farbvalenz aus der Spektralverteilung des Lichtstrahls ermittelt. Solche Rechenverfahren modellieren die farbphysiologischen Eigenschaften des Auges auf mathematische Weise.

Erläuterung

Farbvalenz und Spektralverteilung

Elektromagnetische Strahlung löst, sofern sie Wellenlängen aus dem sichtbaren Bereich enthält, im Auge eine Farbempfindung aus. Welche Farbe empfunden wird, hängt hauptsächlich vom Anteil der verschiedenen sichtbaren Wellenlängen im Gemisch ab, also von der Spektralverteilung des Lichtes.

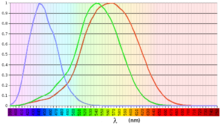
Die drei Farbrezeptor-Typen im menschlichen Auge sprechen auf verschiedene Wellenlängen-Bereiche an.

Da das menschliche Auge jedoch zur Farbunterscheidung nur drei verschiedene Arten von Farbrezeptoren besitzt, ist die Anzahl der möglichen verschiedenen Farbwahrnehmungen kleiner als die Anzahl der möglichen verschiedenen Spektralverteilungen des Lichtes.^{[Anm.
1]} Ein Farbrezeptor kann nicht unterscheiden, auf welcher Wellenlänge in seinem Empfindlichkeitsbereich er gereizt wird, er kann nur stärkere und schwächere Reize unterscheiden. Gleich starke Reize können erzeugt werden

durch stärkeres Licht mit einer Wellenlänge, für die der Rezeptor weniger empfindlich ist, oder
durch schwächeres Licht mit einer Wellenlänge, für die er empfindlicher ist.^{[Anm.
2]}

Alle Lichtstrahlen mit Spektralverteilungen, welche dieselben Gesamtreize in den drei Rezeptorarten erzeugen, werden (unter gleichen Beobachtungsbedingungen) als gleichfarbig wahrgenommen, auch wenn ihre Spektralverteilungen unterschiedlich sind – sie haben dieselbe Farbvalenz. Werden alle möglichen Spektralverteilungen in Klassen eingeteilt, welche jeweils die als gleichfarbig wahrgenommenen Spektralverteilungen zusammenfassen, so dient die Farbvalenz der eindeutigen Kennzeichnung dieser Klassen.

Anhand der Farbvalenzen zweier Lichtstrahlen lässt sich entscheiden, ob sie gleiche oder verschiedene Farbwahrnehmungen auslösen werden:

Zwei Lichtstrahlen gleicher Farbvalenz werden unter gleichen Beobachtungsbedingungen als gleichfarbig wahrgenommen, auch wenn sich ihre Spektralverteilungen unterscheiden.
Zwei Lichtstrahlen verschiedener Farbvalenzen dagegen werden unter sonst gleichen Beobachtungsbedingungen als verschiedenfarbig wahrgenommen (sofern der Unterschied groß genug ist, um die Farbunterscheidungsschwelle des Auges zu überschreiten).

Farbvalenz und Farbwahrnehmung

Die Farbvalenz ist eine objektiv messtechnisch bestimmbare (z.B. aus der Spektralverteilung ableitbare) Eigenschaft des Lichtes, das als physikalischer Farbreiz auf das Auge einwirkt. Sie bestimmt, welcher Sinnesreiz in den Sinneszellen und Nerven des Auges ausgelöst wird, beschreibt aber nicht, als welche Farbe dieser Sinnesreiz im Bewusstsein des Beobachters wahrgenommen wird.

Diese Farbwahrnehmung ist ein komplexer physiologischer Prozess, in den zahlreiche Nichtlinearitäten sowie Kontrast- und Nachwirkungseffekte einfließen, welche sich nur schwer formelmäßig erfassen lassen. So wird Licht, das in dunklem Umfeld als ein nicht allzu gesättigtes „Orange“ wahrgenommen wird, in sehr hellem Umfeld als „Braun“ wahrgenommen. In grünem Umfeld erscheint die Farbe als „Rotbraun“, in rotem Umfeld als „Gelblichbraun“. Ein Lichtstrahl mit gegebener Farbvalenz kann also auf verschiedene Weise wahrgenommen werden, wenn er in Umfeldern mit verschiedenen Helligkeits- und Farbkontrastbedingungen gesehen wird. Andererseits werden zwei Lichter mit untereinander gleicher Farbvalenz zwar wie im genannten Beispiel als verändert wahrgenommen, wenn sich die Beobachtungsbedingungen ändern, beide ändern sich jedoch auf die gleiche Weise und bewahren ihre Gleichheit untereinander.

Ähnliches gilt für die Umstimmung des Auges: Ist das Auge einer Szene mit einer dominierenden Gesamtfärbung ausgesetzt (beispielsweise in einem Zimmer mit rötlichem Glühlampenlicht), so passt es sich der Situation an, so dass die Gesamtfärbung als neutraler empfunden wird und sich im Zuge dieser Umstimmung die wahrgenommenen Farben der einzelnen Gegenstände ändern. Die Umstimmung wirkt sogar eine Weile nach: Wird ein Auge geschlossen und so vor der Umstimmung geschützt, dann werden die beiden Augen nach Verlassen des Zimmers die sonnenbeschienene Landschaft verschiedenfarbig wahrnehmen, bis wieder eine gemeinsame Umstimmung erreicht ist.

Wesentlich für die Anwendbarkeit der Farbvalenz ist jedoch, dass das umgestimmte Auge zwei gleiche Farben zwar als verändert, aber als in gleicher Weise verändert und daher nach wie vor als untereinander gleich empfindet. Die Farbstimmung beeinflusst also die Farbwahrnehmung, aber nicht das Gleichheitsurteil des Auges. Der Persistenzsatz des Physiologen J. v. Kries (1878) besagt daher:

„Verschieden zusammengesetzte Farbreize, die dem neutral gestimmten Auge gleich erscheinen (metamer sind), erscheinen auch dem irgendwie umgestimmten Auge gleich.^{[Anm.
3]}“

Das Urteil des Auges über Gleichheit oder Ungleichheit zweier Farben ist also unabhängig von den Beobachtungsbedingungen reproduzierbar. Damit wird eine eindeutige Bestimmung der Farbvalenz möglich: Zwei Farbreize haben genau dann gleiche Farbvalenz, wenn sie bei einem Farbvergleich ununterscheidbar sind.

Das Auge selbst ist über das Gleichheitsurteil hinaus kaum zu einer reproduzierbaren quantitativen Bestimmung seiner Farbwahrnehmung fähig. Dies genügt jedoch, um die Farbvalenz eindeutig und quantitativ messbar zu machen: Wird dem Auge die zu messende Farbvalenz im unmittelbaren Vergleich mit einer additiven Mischung bekannter Farbvalenzen angeboten und stellt Gleichheit fest, dann ist die zu messende Farbvalenz durch die bekannten Intensitäten der gemischten Vergleichs-Farbvalenzen quantitativ bestimmt. Da die gemischten Farbreize objektiv physikalisch messbar sind, gilt dasselbe für die ermittelte Farbvalenz.

Eigenschaften

Additive Farbmischung

Bei der additiven Farbmischung werden verschiedenfarbige Lichtstrahlen einander überlagert.

Die Farbvalenz beschreibt eine Eigenschaft eines Lichtstrahls, die linear (siehe → Spektralwerte) von dessen Spektralverteilung abhängt. Überlagern sich zwei Lichtstrahlen, so ist das Spektrum des Summenstrahls gleich der Summe der beiden überlagerten Spektren. Aufgrund des linearen Zusammenhangs zwischen Farbvalenz und Spektrum ist daher die Farbvalenz des Summenstrahls gleich der Summe der Farbvalenzen der beiden überlagerten Lichtstrahlen. Eine additive Farbmischung lässt sich also einfach durch die Addition der Farbvalenzen der gemischten Lichtstrahlen beschreiben. Mit Hilfe der Farbvalenz lässt sich zwar nicht eindeutig vorhersagen, wie eine durch additive Farbmischung erzeugte Farbe wahrgenommen wird, da die Wahrnehmung auch von den jeweiligen Beobachtungsbedingungen beeinflusst ist. Es lässt sich vorhersagen, mit welcher Farbvalenz die Mischung unter gleichen Beobachtungsbedingungen als gleichfarbig wahrgenommen werden wird, oder welche Farbvalenzen additiv gemischt werden müssen, um eine Ziel-Farbvalenz herzustellen.

Ein Lichtstrahl gegebener Farbvalenz sei durch geeignete additive Mischung von Lichtstrahlen anderer Farbvalenzen „nachgestellt“ worden – die Mischung sei also so gewählt, dass das gemischte Licht dieselbe Farbvalenz aufweist wie das Originallicht. Die Spektralverteilungen des originalen und des nachgestellten Lichtstrahls werden im Allgemeinen trotz gleicher Farbvalenz verschieden sein. Wird nun sowohl dem originalen als auch dem nachgestellten Lichtstrahl Licht einer weiteren Farbvalenz überlagert (additiv zugemischt), so ist erfahrungsgemäß in beiden Fällen das Mischergebnis dasselbe. Ausschlaggebend für das Mischergebnis ist also nicht die Spektralverteilung der beteiligten Lichtstrahlen. Die Kenntnis der Farbvalenzen genügt, um das Mischergebnis vorhersagen zu können.^{[Anm. 4]}

Da die Auswirkung eines in eine additive Farbmischung eingebrachten Lichtstrahls auf das Mischungsergebnis also nur von dessen Farbvalenz und nicht von seiner Spektralverteilung abhängt (Drittes Graßmannsches Gesetz), lässt sich die Farbvalenz über ihr Verhalten in additiven Farbmischungen definieren:

„Die Farbvalenz ist diejenige Eigenschaft einer (ins Auge einfallenden) Strahlung (‚Farbreiz‘), die das Verhalten dieses Farbreizes in der additiven Mischung mit anderen Farbreizen bestimmt; sie beschreibt die ‚Wertigkeit‘ der Strahlung für die additive Mischung.“

Vektoren

→ Hauptartikel: Vektor

Wie die Erfahrung zeigt, sind zur Beschreibung einer Farbvalenz stets drei^{[Anm.
5]} Kennzahlen nötig (Erstes Graßmannsches Gesetz). Farben sind in diesem Sinne also „dreidimensionale“ Größen, und Farbräume sind dreidimensionale mathematische Räume. (Dies hängt letztlich mit der Existenz von drei Arten von Farbrezeptoren im Auge zusammen.) Da Farbvalenzen sich bei der additiven Farbmischung außerdem rechnerisch additiv verhalten, zeigen sie mathematische Eigenschaften dreidimensionaler Vektoren, so dass die Regeln der Vektorrechnung auf sie angewendet werden können.

Basisvektoren und Vektorkomponenten

Werden drei beliebige dreidimensionale Vektoren $\mathbf {A}$ , $\mathbf {B}$ und ${\mathbf {C}}$ mit der einzigen Einschränkung gewählt, dass sie nicht in einer gemeinsamen Ebene liegen dürfen, dann können alle dreidimensionalen Vektoren $\mathbf{V}$ als Summe von geeigneten Vielfachen dieser so genannten Basisvektoren dargestellt werden,

$\mathbf{V} = A \cdot \mathbf{A} + B \cdot \mathbf{B} + C \cdot \mathbf{C}$ ,

und ein Vektor $\mathbf{V}$ ist eindeutig bestimmt, wenn seine „Komponenten“ , und bezüglich der Basisvektoren $\mathbf {A}$ , $\mathbf {B}$ und ${\mathbf {C}}$ gegeben sind. Der Vektor kann daher in der „Komponentendarstellung“ geschrieben werden:

$\mathbf{V} = (A, B, C)$ .

Vektoraddition

Sind zwei Vektoren $\mathbf{V_1}$ und $\mathbf{V_2}$ mit den Komponenten (A_1, B_1, C_1) und (A_2, B_2, C_2) gegeben, dann ergibt sich der Summenvektor $\mathbf{V_1} + \mathbf{V_2}$ durch komponentenweise Addition:

$\mathbf{V_1} + \mathbf{V_2} = (A_1+A_2, B_1+B_2, C_1+C_2)$ .

Multiplikation mit einer Zahl

Ein Vektor kann mit einer Zahl multipliziert werden, das Ergebnis ist ein -mal so langer Vektor. In der Komponentenschreibweise sind alle Komponenten mit jener Zahl zu multiplizieren:

$n \cdot \mathbf{V} = n \cdot(A, B, C) = (n \cdot A, n \cdot B, n \cdot C)$

Basiswechsel

→ Hauptartikel: Basiswechsel (Vektorraum)

Die Basisvektoren müssen nicht senkrecht aufeinander stehen, und sie müssen nicht gleich lang sein. Sie können so gewählt werden, wie es für die jeweilige Aufgabenstellung am bequemsten ist. Wird ein anderer Satz von Basisvektoren genutzt, so ändern sich die Komponenten des betrachteten Vektors $\mathbf{V}$ . Die Umrechnung der auf die erste Basis bezogenen Komponenten in die auf die zweite Basis bezogenen Komponenten geschieht wie folgt:

Ist neben den Basisvektoren $\mathbf{A}, \mathbf{B}, \mathbf{C}$ ein zweiter Satz von Basisvektoren $\mathbf{A'}, \mathbf{B'}, \mathbf{C'}$ gegeben, und sind die Komponenten der gestrichenen Basisvektoren in Bezug auf die ungestrichenen Basisvektoren bekannt,

$\begin{align} \mathbf{A'} = a_{11} \mathbf{A} + a_{12} \mathbf{B} + a_{13} \mathbf{C} \\ \mathbf{B'} = a_{21} \mathbf{A} + a_{22} \mathbf{B} + a_{23} \mathbf{C} \\ \mathbf{C'} = a_{31} \mathbf{A} + a_{32} \mathbf{B} + a_{33} \mathbf{C} \end{align}$ ,

so sind die Komponenten der ungestrichenen Basisvektoren in Bezug auf die gestrichenen Basisvektoren bekannt, und es ist

$\begin{align} \mathbf{A} = b_{11} \mathbf{A'} + b_{12} \mathbf{B'} + b_{13} \mathbf{C'} \\ \mathbf{B} = b_{21} \mathbf{A'} + b_{22} \mathbf{B'} + b_{23} \mathbf{C'} \\ \mathbf{C} = b_{31} \mathbf{A'} + b_{32} \mathbf{B'} + b_{33} \mathbf{C'} \end{align}$ ,

wobei die aus den $b_{{ij}}$ gebildete Koeffizientenmatrix die Inverse zu der aus den $a_{ij}$ gebildeten Koeffizientenmatrix ist.

Ein gegebener Vektor kann bezüglich beider Sätze von Basisvektoren ausgedrückt werden:

${\begin{aligned}&\,A'\cdot \mathbf {A'} +B'\cdot \mathbf {B'} +C'\cdot \mathbf {C'} \\=&\,V\\=&\,A\cdot \mathbf {A} +B\cdot \mathbf {B} +C\cdot \mathbf {C} \\=&\,A\cdot (b_{11}\mathbf {A'} +b_{12}\mathbf {B'} +b_{13}\mathbf {C'} )+B\cdot (b_{21}\mathbf {A'} +b_{22}\mathbf {B'} +b_{23}\mathbf {C'} )+C\cdot (b_{31}\mathbf {A'} +b_{32}\mathbf {B'} +b_{33}\mathbf {C'} )\\=&\,(b_{11}A+b_{21}B+b_{31}C)\mathbf {A'} +(b_{12}A+b_{22}B+b_{32}C)\mathbf {B'} +(b_{13}A+b_{23}B+b_{33}C)\mathbf {C'} \end{aligned}}$

Vergleich der ersten und der letzten Zeile zeigt, dass die Vektorkomponenten (A', B', C') bezüglich der gestrichenen Basis folgendermaßen mit den Komponenten (A, B, C) bezüglich der ungestrichenen Basis zusammenhängen:

$\begin{align} A' = b_{11}\ A + b_{21}\ B + b_{31}\ C \\ B' = b_{12}\ A + b_{22}\ B + b_{32}\ C \\ C' = b_{13}\ A + b_{23}\ B + b_{33}\ C \end{align}$

Analog ergibt sich für die Umrechnung in umgekehrter Richtung:

$\begin{align} A = a_{11}\ A' + a_{21}\ B' + a_{31}\ C' \\ B = a_{12}\ A' + a_{22}\ B' + a_{32}\ C' \\ C = a_{13}\ A' + a_{23}\ B' + a_{33}\ C' \end{align}$

Farbvalenzen als Vektoren

In der Farbmetrik werden die Farbvalenzen als Vektoren $\mathbf {F}$ behandelt, insbesondere gelten die soeben erläuterten Rechenregeln für Vektoren. Die Gesamtheit aller (möglicher) Farbvalenz-Vektoren bildet den dreidimensionalen Farbraum, die Spitze jedes Farbvalenz-Vektors markiert einen Farbort im Farbraum.

Farbwert

Die Länge eines Farbvalenz-Vektors heißt Farbwert. Ist eine Farbvalenz $\mathbf {F}$ als additive Mischung zweier Farbvalenzen $\mathbf {A}$ und $\mathbf {B}$ gegeben

$\mathbf{F} = A \cdot \mathbf{A} + B \cdot \mathbf{B}$

so sind und die Farbwerte, mit denen $\mathbf {A}$ und $\mathbf {B}$ in der Mischung vorkommen, die Farbvalenz $\mathbf {F}$ kann daher (bezüglich der gegebenen Farbvalenzen $\mathbf {A}$ und $\mathbf {B}$ ) auch in der Komponentendarstellung mit den Farbwerten (A,B) geschrieben werden. Die Einheiten der Farbwerte sind zunächst durch die willkürlich gewählten Längen der Basisvektoren $\mathbf {A}$ und $\mathbf {B}$ bestimmt (zur Wahl eines Maßstabs siehe die Abschnitte →Skalierung und Weißpunkt und →Helligkeit von Licht- und Körperfarben).

Farbart

Werden die Helligkeiten der beiden additiv gemischten Lichtstrahlen mit den Farbvalenzen $\mathbf {A}$ und $\mathbf {B}$ um denselben Faktor geändert, so ändert sich erfahrungsgemäß das Mischungsergebnis nur bezüglich seiner Helligkeit. Eine Familie von Farben, die sich nur in der Helligkeit voneinander unterscheiden, heißt Farben gleicher Farbart^{[Anm. 6]}

In der Vektorsummendarstellung hat der neue Summenvektor

$n A \cdot \mathbf{A} + n B \cdot \mathbf{B} = n (A \cdot \mathbf{A} + B \cdot \mathbf{B}) = n \mathbf{F}$

die fache Länge, aber dieselbe Richtung wie der ursprüngliche Vektor $\mathbf {F}$ . Die Farbart wird also durch die Richtung des Farbvalenz-Vektors angegeben.

Primärvalenzen

Die als Basisvektoren für die Vektorsummen- oder Komponentendarstellung einer beliebigen Farbvalenz gewählten Basis-Farbvalenzen heißen Primärvalenzen. Ist ein Satz von drei Primärvalenzen $\mathbf{A}, \mathbf{B}, \mathbf{C}$ gewählt, so lässt sich jede Farbvalenz $\mathbf {F}$ (da dreidimensional) als Vektorsumme der drei Primärvalenzen darstellen:

$\mathbf{F} = A \cdot \mathbf{A} + B \cdot \mathbf{B} + C \cdot \mathbf{C}$

oder in der Komponentendarstellung als Tripel von Farbwerten:

$\mathbf{F} = (A, B, C)$ .

Wechsel der Primärvalenzen

Die Primärvalenzen können im Prinzip beliebig gewählt werden. Die Umrechnung der Farbwerte, die eine Farbvalenz bezüglich der alten Primärvalenzen beschreiben, in die Farbwerte, die sie bezüglich der neuen Primärvalenzen beschreiben, geschieht analog zu den oben erläuterten Rechenregeln für den Basiswechsel in der Vektorrechnung. Diese Operation wird in der Farbmetrik häufig benutzt. Sie erlaubt beispielsweise die Messung von Farbvalenzen bezüglich eines der Messung leicht zugänglichen Satzes von Primärvalenzen, während die praktische Anwendung bezüglich eines in anderer Hinsicht bequemen Satzes von Primärvalenzen erfolgen kann.

Abneysches Gesetz

Gemäß dem Abneyschen Gesetz (nach William de Wiveleslie Abney) gilt für die Leuchtdichte einer Farbvalenz $\mathbf {F}$ mit den Farbwerten (A, B, C) :

$L = L_A \cdot A + L_B \cdot B + L_C \cdot C$ .

D.h. die Helligkeit einer Farbvalenz ist umso größer, je größer ihre Farbwerte sind. Jede der Primärvalenzen $\mathbf {A}$ , $\mathbf {B}$ und ${\mathbf {C}}$ trägt dabei proportional zu ihrem Farbwert , und zur Gesamtleuchtdichte der Farbvalenz bei. Die Proportionalitätsfaktoren $L_{A},L_{B},L_{C}$ heißen Leuchtdichte-Beiwerte; sie sind die Leuchtdichten der Einheitsbeträge der betreffenden Primärvalenzen.

Die durch das Abneysche Gesetz beschriebene Additivität gilt im Allgemeinen nur für photometrische Größen^{[Anm.
7]} wie die Leuchtdichte. Für die wahrgenommene Helligkeit gilt sie nur näherungsweise und nur in Fällen geringer Farbintensität.

Messung

Eine typische Anordnung zur direkten Messung von Farbvalenzen zeigt dem Beobachter ein von einem neutralen Umfeld umgebenes Farbfeld, das in zwei Hälften geteilt ist. Die eine Hälfte enthält die nachzustellende Farbe (erzeugt beispielsweise durch einen Projektor mit Farbfilter, durch einen Farbkreisel), die unmittelbar benachbarte zweite Hälfte enthält eine additive Mischung der für den Versuch verwendeten Primärvalenzen (erzeugt beispielsweise durch Projektoren mit geeigneten Farbfiltern).

Der Beobachter regelt die Intensitäten der Primärvalenzen, bis beide Hälften des Farbfeldes gleichfarbig erscheinen. Durch die Versuchsbedingungen ist sichergestellt, dass beide Farbreize unter denselben Beobachtungsbedingungen betrachtet werden, aus der Gleichheit der Farbwahrnehmung also auf die Gleichheit der Farbvalenzen geschlossen werden kann. Die eingestellten Intensitäten entsprechen nach Kalibrierung den Farbwerten der nachgestellten Farbvalenz.

Von besonderem Interesse ist es, die Spektralfarben nachzustellen. Sind deren Farbwerte bekannt (→Spektralwerte), so lassen sich die Farbwerte aller anderen Farbvalenzen bei bekannter Spektralverteilung rechnerisch ermitteln.

Farbwertanteile und Farbtafeln

Die Farbarten aller aus drei gegebenen Farbvalenzen additiv ermischbaren Farbvalenzen liegen in einer Farbtafel innerhalb eines Dreiecks, dessen Ecken durch die Farbarten der gegebenen Farbvalenzen markiert werden.

Die dreidimensionale Natur der Farbvalenz-Vektoren macht es schwierig, sie anschaulich darzustellen. Da die Helligkeit oft von geringerem Interesse als die Farbart einer Farbvalenz ist, kann von den Farbwerten (A, B, C) einer Farbvalenz zu den Farbwertanteilen übergegangen werden, indem jeder der drei Farbwerte durch die Summe aller drei Farbwerte dividiert wird:

$\begin{align} a = \frac{A}{A + B + C} \\ b = \frac{B}{A + B + C} \\ c = \frac{C}{A + B + C} \end{align}$

Wegen a + b + c = 1 lässt sich stets eine der drei Größen (a, b, c) aus den beiden anderen berechnen, trägt also keine unabhängige Information und kann ohne Verlust fortgelassen werden. Die beiden übrigen Farbwertanteile, beispielsweise und , lassen sich in einem zweidimensionalen Diagramm auftragen.

Die obigen Formeln lassen sich auffassen als Projektion der Farbvalenz-Vektoren auf die Ebene im Farbraum, die durch die Bedingung A + B + C = 1 beschrieben wird. Diese Ebene liegt schräg im Farbraum und geht durch die Spitzen der Primärvalenz-Vektoren $\mathbf {A}$ , $\mathbf {B}$ und ${\mathbf {C}}$ . Alle Vektoren mit derselben Richtung (also derselben Farbart) durchstoßen diese Ebene im selben Punkt (a, b) , welcher daher die betreffende Farbart repräsentiert. Das zweidimensionale (a, b) -Diagramm in dieser Ebene ist also eine „Farbarttafel“ oder kurz Farbtafel. Auf ihr sind alle Farbvalenzen nach ihrer Farbart und unter Verzicht auf die Helligkeitsinformation angeordnet. 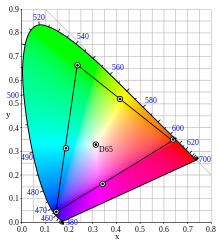Die bekannteste dieser Farbtafeln ist die CIE-Normfarbtafel.

Aus der Konstruktion der Farbtafel folgt, dass die Farbarten aller Farbvalenzen, die sich als additive Mischung aus zwei gegebenen Farbvalenzen darstellen lassen, in der Farbtafel auf der Verbindungsgeraden zwischen den gegebenen Farbarten liegen. Werden drei Farbvalenzen additiv gemischt, so liegen die Farbarten aller daraus ermischbaren Farbvalenzen in der Farbtafel in einem Dreieck, dessen Ecken von den Farbarten der drei gegebenen Farbvalenzen gebildet werden. Die Abbildung zeigt ein solches Gamut-Dreieck am Beispiel der CIE-Normfarbtafel.

Innere und äußere Mischung

Die Komponenten eines mathematischen Vektors $\mathbf{V} = (A_V, B_V, C_V)$ können sowohl positives als auch negatives Vorzeichen haben. Die Farbwerte einer Farbvalenz $\mathbf{F} = (A, B, C)$ können als Intensitäten eines Satzes von additiv gemischten Primärvalenzen aufgefasst werden. Da Licht keine negative Intensität haben kann, scheinen zunächst nur positive Farbwerte möglich zu sein. Es erweist sich jedoch als vorteilhaft, auch negative Farbwerte rechnerisch zuzulassen.

Werden die drei Primärvalenz-Vektoren unendlich verlängert angenommen und das zwischen ihnen aufgespannte Volumen betrachtet (eine unendlich lange „Tüte“ mit dreieckigem Querschnitt), so liegen alle Farbvalenzen, die eine Summe aus positiven Vielfachen der Primärvalenzen sind und daher drei positive Farbwerte besitzen, im Inneren dieses Volumens (die Schnittfigur dieses Volumens mit der Farbtafelebene ist das im letzten Abschnitt erwähnte Gamut-Dreieck); die außerhalb dieses Volumens liegenden Farbvalenzen haben mindestens einen negativen Farbwert.

Für das Rechnen mit Farbvalenzen sind negative Farbwerte kein Hindernis. Wirklich additiv ermischbar und „zeigbar“ sind aber nur Farbvalenzen mit ausschließlich positiven Farbwerten, sofern die drei Primärvalenzen „zeigbar“ sind.

Innere Mischung

Eine additive innere Mischung liegt vor, wenn sie nur positive Anteile der gemischten Primärvalenzen enthält. Die Mischvalenz liegt in diesem Fall innerhalb des Volumens, das von den Primärvalenzen aufgespannt wird, d.h. innerhalb des Gamut-Dreiecks der Farbtafel.

Äußere Mischung

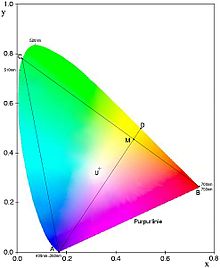
Äußere Mischung: Farbvalenz D liegt außerhalb des Gamut-Dreiecks von A, B und C. Sie kann durch Zumischung von A auf den Rand des Dreiecks gebracht und dort aus B und C additiv ermischt werden.

Eine additive äußere Mischung liegt vor, wenn die Zielvalenz negative Farbwerte besitzt. Sie liegt daher außerhalb des Volumens, das aus den gegebenen Primärvalenzen additiv ermischt werden kann, d.h. außerhalb des Gamut-Dreiecks der Farbtafel.

Soll bei einer farbmetrischen Messung, die nur mit wirklich „zeigbaren“ Farben arbeiten kann, eine gegebene Farbvalenz $\mathbf{D}$ durch additive Mischung dreier durch die Messapparatur vorgegebener Primärvalenzen $\mathbf{A}, \mathbf{B}, \mathbf{C}$ nachgestellt werden, so ist das nicht möglich, wenn sie bezüglich mindestens einer dieser Primärvalenzen negative Farbwerte besitzt (vgl. Abb.).

In diesem Fall lässt sich ein Trick nutzen. Beispielsweise solle die Farbvalenz

$\mathbf {D} =B\ \mathbf {B} +C\ \mathbf {C} -A\ \mathbf {A}$

mit negativem Farbwert nachgestellt werden durch additive Mischung von $\mathbf {A}$ , $\mathbf {B}$ und ${\mathbf {C}}$ . Durch Umstellen

$\Leftrightarrow \mathbf {D} +A\ \mathbf {A} =B\ \mathbf {B} +C\ \mathbf {C}$

kann daraus eine Farbgleichung mit ausschließlich positiven Farbwerten gemacht werden. Instrumentell bedeutet dies, dass der Zielvalenz ein positiver Anteil $+A$ der Primärvalenz $\mathbf {A}$ zugemischt und so eine neue Zielvalenz erzeugt wird, die durch die Primärvalenzen $\mathbf {B}$ und ${\mathbf {C}}$ mit positiven Farbwerten nachgestellt werden kann. Obwohl die ursprüngliche Zielvalenz nun nicht mehr angezeigt wird, gibt die gefundene Einstellung unter korrekter Berücksichtigung der Vorzeichen eindeutig deren Farbwerte an.

In einer Farbtafel (vgl. Diagramm) bedeutet dieses Vorgehen, dass eine Farbart $\mathbf{D}$ , die außerhalb des durch die Primärvalenzen $\mathbf {A}$ , $\mathbf {B}$ und ${\mathbf {C}}$ aufgespannten Gamut-Dreiecks liegt, durch Zumischen einer geeigneten Menge von $\mathbf {A}$ auf die nächstgelegene Dreiecksseite $\mathbf{BC}$ gebracht wird (auf Punkt ${\mathbf {M}}$ ); dann kann ${\mathbf {M}}$ auf gewohnte Weise aus den beiden Primärvalenzen $\mathbf {B}$ und ${\mathbf {C}}$ , die diese Seite aufspannen, additiv ermischt werden.

Negative Farbwerte einer gegebenen Farbvalenz lassen sich stets durch geeignete Wahl der Primärvalenzen vermeiden. Sie sind also nur eine Eigenschaft der Darstellung einer Farbvalenz durch Farbwerte bezüglich eines gegebenen Satzes von Primärvalenzen, aber keine Eigenschaft der Farbvalenz selbst. In einer Farbtafel bedeutet dies, dass zu jedem Farbpunkt (bzw. zu den meisten) ein Dreieck aus Primärvalenzen gefunden werden kann, in dem er enthalten ist.

Spektralwerte

Da ein Lichtstrahl beliebiger Spektralverteilung sich stets als additive Mischung monochromatischer Lichtstrahlen (d.h. der einzelnen im Gemisch enthaltenen „Spektralfarben“) auffassen lässt, kann die Farbvalenz des Lichtstrahls als Summe der Farbvalenzen der beteiligten Spektralfarben berechnet werden, wenn die Farbvalenzen, die den einzelnen Spektralfarben zukommen, sowie die Anteile der Spektralfarben am Gemisch bekannt sind.

Sei $\varphi_{\lambda}$ die Spektralverteilung^{[Anm.
8]} des betrachteten Lichtstrahls. Auf ein kleines die Wellenlänge $\lambda _{i}$ enthaltendes Wellenlängenintervall $\mathrm{\Delta}\lambda_i$ entfällt dann die Strahlungsleistung $\varphi_{\lambda i} \, \mathrm{\Delta}\lambda_i$ . Der gesamte Lichtstrahl $\Phi$ ist eine additive Mischung aus „monochromatischen“ Lichtstrahlen $\Phi_{\lambda i}$ (also Lichtstrahlen, die nur einen kleinen Wellenlängenbereich $\mathrm{\Delta}\lambda_i$ umfassen). Die Farbvalenz $\mathbf {F}$ des Lichtstrahls ist also die Summe der Farbvalenzen $\mathbf{F}_{\lambda i}$ der monochromatischen Lichtanteile $\Phi_{\lambda i}$ :

$\mathbf{F} = \sum_i \mathbf{F}_{\lambda i} \ \mathrm{\Delta}\lambda_i$ .

Sie lässt sich andererseits – wie immer – ausdrücken als ein Tripel von Farbwerten bezüglich eines gegebenen Satzes von Primärvalenzen $\mathbf{A}, \mathbf{B}, \mathbf{C}$ :

$\mathbf{F} = A \, \mathbf{A} + B \, \mathbf{B} + C \, \mathbf{C}$ .

Energiegleiches Spektrum und Farbgleichung

Von besonderem Interesse ist in der Farbmetrik jene Spektralverteilung $\varepsilon_{\lambda}$ , welche für alle Wellenlängen denselben Wert hat:

$\varepsilon_{\lambda} = const.$ .

Diese Spektralverteilung wird als „energiegleiches Spektrum“ bezeichnet.

Für die Farbvalenz $\mathbf{E}_{\lambda i}$ eines monochromatischen Lichtstrahls aus einem energiegleichen Spektrum gilt bezüglich der Primärvalenzen $\mathbf{A}, \mathbf{B}, \mathbf{C}$ die Farbgleichung:

$\mathbf{E}_{\lambda i} = \bar{a}(\lambda_i) \, \mathbf{A} + \bar{b}(\lambda_i) \, \mathbf{B} + \bar{c}(\lambda_i) \, \mathbf{C}$ .

Spektralwerte

Beispiel: Die Spektralwertfunktionen $\bar x, \bar y, \bar z$ , die bezüglich der Norm-Primärvalenzen X, Y, Z ermittelt wurden.

Die Farbwerte $\bar{a}(\lambda_i), \bar{b}(\lambda_i), \bar{c}(\lambda_i)$ für einen monochromatischen Lichtstrahl der Wellenlänge $\lambda _{i}$ , der aus Licht mit energiegleichem Spektrum entnommen wurde, heißen Spektralwerte. Sie werden üblicherweise durch überstrichene Kleinbuchstaben bezeichnet. (Man beachte den Gebrauch von Kleinbuchstaben, obwohl es sich um Farbwerte und nicht um Farbwertanteile handelt. Der Überstrich erinnert an das energiegleiche Spektrum).

Bei der messtechnischen Erfassung der Spektralwerte ist es schwierig, tatsächlich ein energiegleiches Spektrum herzustellen. Stattdessen lässt sich ein beliebiges Spektrum $\varphi_{\lambda}$ nutzen, die Strahlungsleistung $\varphi_{\lambda i} \, \mathrm{\Delta} \lambda_i$ messen, die jeweils auf das betrachtete Wellenlängenintervall $\mathrm{\Delta} \lambda_i$ entfällt, und die gemessenen Farbwerte durch den Skalierungsfaktor $\varphi_{\lambda i}$ dividieren, um sie in die Spektralwerte für die betreffende Wellenlänge zu überführen.

Falls statt einer absoluten eine wesentlich einfachere relative Messung der Strahlungsleistung $\varphi_{\lambda i} \, \mathrm{\Delta} \lambda_i$ erfolgt, so sind die Farbwerte (A, B, C) , die mit Hilfe der Spektralwerte aus der Spektralverteilung ermittelt wurden, nur bis auf eine unbekannte Konstante bestimmt. Sind lediglich die Verhältnisse der Farbwerte von Interesse (z.B. in Gestalt der Farbwertanteile), so kürzt sich diese Konstante fort. Sind dagegen die Farbwerte selbst von Interesse, so kann über die Konstante auf verschiedene Weise verfügt werden, siehe hierzu den Abschnitt →Helligkeit von Licht- und Körperfarben.

Die Farbvalenz $\mathbf {F}$ eines beliebigen Lichtstrahls $\Phi$ mit dem Spektrum $\varphi_{\lambda}$ bezüglich gegebener Primärvalenzen $\mathbf{A}, \mathbf{B}, \mathbf{C}$ lässt sich bestimmen, wenn die Spektralwerte $\bar{a}(\lambda), \bar{b}(\lambda), \bar{c}(\lambda)$ bezüglich dieser Primärvalenzen bekannt sind. Der monochromatische Teil-Lichtstrahl $\Phi_{\lambda i}$ hat im Wellenlängenintervall $\mathrm{\Delta} \lambda_i$ eine um den Faktor $k \varphi_{\lambda i}$ größere Strahlungsleistung als der Teil-Lichtstrahl gleicher Wellenlänge im energiegleichen Spektrum, also ist der betreffende Farbvalenz-Vektor $\mathbf{F}_{\lambda i}$ um den Faktor $k \varphi_{\lambda i}$ länger als der Farbvalenz-Vektor $\mathbf{E}_{\lambda i}$ :

$\mathbf{F}_{\lambda i} = \mathbf{E}_{\lambda i} \cdot k \varphi_{\lambda i}$

In der Summe über alle Wellenlängenintervalle ergibt sich

$\begin{align} A \, \mathbf{A} + B \, \mathbf{B} + C \, \mathbf{C} = \mathbf{F} & = \sum_i \mathbf{F}_{\lambda i} \, \mathrm{\Delta}\lambda_i \\ & = \sum_i \mathbf{E}_{\lambda i} \, k \varphi_{\lambda i} \, \mathrm{\Delta}\lambda_i \\ & = k \sum_i \left( \bar{a}(\lambda_i) \, \mathbf{A} + \bar{b}(\lambda_i) \, \mathbf{B} + \bar{c}(\lambda_i) \, \mathbf{C} \right) \, \varphi_{\lambda i} \, \mathrm{\Delta}\lambda_i \\ & = \left(k \sum_i \bar{a}(\lambda_i) \, \varphi_{\lambda i} \, \mathrm{\Delta}\lambda_i \right) \mathbf{A} + \left(k \sum_i \bar{b}(\lambda_i) \, \varphi_{\lambda i} \, \mathrm{\Delta}\lambda_i \right) \mathbf{B} + \left(k \sum_i \bar{c}(\lambda_i) \, \varphi_{\lambda i} \, \mathrm{\Delta}\lambda_i \right) \mathbf{C} \\ \end{align}$

Der Vergleich der ersten und der letzten Zeile zeigt, dass die Farbwerte von $\Phi$ sich aus seiner Spektralverteilung $\varphi_{\lambda}$ berechnen lassen:

$\begin{align} A = k \sum_i \bar{a}(\lambda_i) \, \varphi_{\lambda i} \, \mathrm{\Delta}\lambda_i \\ B = k \sum_i \bar{b}(\lambda_i) \, \varphi_{\lambda i} \, \mathrm{\Delta}\lambda_i \\ C = k \sum_i \bar{c}(\lambda_i) \, \varphi_{\lambda i} \, \mathrm{\Delta}\lambda_i \\ \end{align}$

Werden die Wellenlängenintervalle $\mathrm{\Delta}\lambda_i$ unendlich klein, so gehen die Summen in Integrale über, die sich vom kurzwelligen bis zum langwelligen Ende des sichtbaren Wellenlängenbereichs erstrecken:

$\begin{align} A = k \int_k^l \bar{a}(\lambda) \, \varphi_{\lambda} \, \mathrm{d}\lambda \\ B = k \int_k^l \bar{b}(\lambda) \, \varphi_{\lambda} \, \mathrm{d}\lambda \\ C = k \int_k^l \bar{c}(\lambda) \, \varphi_{\lambda} \, \mathrm{d}\lambda \\ \end{align}$

Die Farbwerte ergeben sich durch Integration über die Spektralverteilung, die mit dem jeweiligen Spektralwert gewichtet wird; dies ist der eingangs erwähnte lineare Zusammenhang zwischen der Spektralverteilung und der zugehörigen Farbvalenz. In der Praxis werden jedoch üblicherweise die o.g. Summen verwendet, da die Spektralwerte meist tabelliert vorliegen.

Zwei Lichtstrahlen mit den Spektralverteilungen $\varphi_{\lambda}$ und $\psi_{\lambda}$ haben die gleiche Farbvalenz, wenn gilt

$\begin{align} \int_k^l \bar{a}(\lambda) \, \varphi_{\lambda} \, \mathrm{d}\lambda = \int_k^l \bar{a}(\lambda) \, \psi_{\lambda} \, \mathrm{d}\lambda \\ \int_k^l \bar{b}(\lambda) \, \varphi_{\lambda} \, \mathrm{d}\lambda = \int_k^l \bar{b}(\lambda) \, \psi_{\lambda} \, \mathrm{d}\lambda \\ \int_k^l \bar{c}(\lambda) \, \varphi_{\lambda} \, \mathrm{d}\lambda = \int_k^l \bar{c}(\lambda) \, \psi_{\lambda} \, \mathrm{d}\lambda \\ \end{align}$

Die Spektralwert-Funktionen müssen (für gegebene Beobachtungsbedingungen) nur ein für alle Mal experimentell bestimmt werden. Es genügt sogar, sie nur einmal für einen bestimmten Satz von Primärvalenzen zu ermitteln, da die Spektralwert-Funktionen für andere Primärvalenzen daraus durch einen Basiswechsel abgeleitet werden können (s.o.).

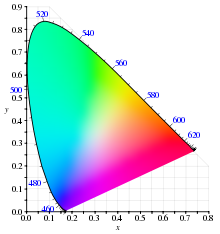
Spektralfarbenzug und virtuelle Farben

Spektralfarbenzug in einer xy-Farbtafel: gekrümmte schwarze Linie. Die reellen Farben liegen innerhalb des Spektralfarbenzugs, die virtuellen außerhalb. Die blauen Zahlen geben die Wellenlängen der Spektralfarben in nm an.

Werden aus den Spektralwerten $\bar{a}(\lambda)$ , $\bar{b}(\lambda)$ und $\bar{c}(\lambda)$ die Spektralwertanteile gebildet

$\begin{align} a(\lambda) = \frac{\bar{a}(\lambda)}{\bar{a}(\lambda) + \bar{b}(\lambda) + \bar{c}(\lambda)} \\ b(\lambda) = \frac{\bar{b}(\lambda)}{\bar{a}(\lambda) + \bar{b}(\lambda) + \bar{c}(\lambda)} \end{align}$

und die Koordinaten $\left(a(\lambda), b(\lambda)\right)$ für alle sichtbaren Wellenlängen $\lambda$ in eine Farbtafel eingetragen, so ergibt sich der „Spektralfarbenzug“ dieser Farbtafel (vgl. Abb.). Der Spektralfarbenzug ist eine überall konvex gekrümmte Kurve.

Reelle Farben

Da sich alle für das Auge sichtbaren Farben als additive Mischungen von Spektralfarben auffassen lassen und additive Mischungen in der Farbtafel stets auf der geraden Verbindungslinie zwischen den beiden gemischten Farbarten liegen, müssen sich alle sichtbaren („reellen“) Farbarten innerhalb des Spektralfarbenzugs befinden.

Alle Farbarten, die aus drei Primärvalenzen durch innere Mischung erhalten werden können, liegen innerhalb des Gamut-Dreiecks, das von den zugehörigen Primärfarbarten in der Farbtafel aufgespannt wird. Da der Bereich reeller Farben durch eine gekrümmte Kurve begrenzt ist, jedes Gamut-Dreieck aber gerade Seiten hat, gibt es kein aus reellen (also innerhalb des Spektralzuges oder auf ihm gelegenen) Primärfarbarten aufgespanntes Gamut-Dreieck, das alle reellen Farben abdecken könnte.

Virtuelle Farben

Punkte außerhalb des Spektralfarbenzugs entsprechen keinen sichtbaren Farbarten, sie haben gleichwohl ihre Farbart-Koordinaten im Diagramm und können rechnerisch genauso behandelt werden wie reelle Farbarten; sie werden als „virtuelle“ (manchmal auch als „imaginäre“) Farbarten bezeichnet.

Werden als Primärvalenzen auch virtuelle Farbvalenzen zugelassen, deren Farbarten außerhalb des Spektralfarbenzuges liegen, dann lassen sie sich so wählen, dass das von ihnen aufgespannte Gamut-Dreieck den Spektralfarbenzug und damit alle sichtbaren Farbarten vollständig umfasst. Beispielsweise wurden die Norm-Primärvalenzen ${\mathbf {X}}$ , ${\mathbf {Y}}$ , ${\mathbf {Z}}$ unter diesem Gesichtspunkt gewählt: Sie selbst liegen außerhalb des Spektralfarbenzuges und sind daher virtuelle Farbvalenzen, aber alle sichtbaren Farbarten lassen sich rechnerisch aus ihnen durch innere Mischung additiv ermischen.

Skalierung und Weißpunkt

→ Weißpunkt

Die Farbwerte , und sind Zahlen, die angeben, welches Vielfache des jeweils zugehörigen Primärvalenz-Vektors $\mathbf {A}$ , $\mathbf {B}$ oder ${\mathbf {C}}$ in einem Farbvalenz-Vektor $\mathbf{F} = A \cdot \mathbf{A} + B \cdot \mathbf{B} + C \cdot \mathbf{C}$ enthalten ist. Eine Farbwert-Einheit ist daher identisch mit der Länge des betreffenden Primärvalenzvektors. Diese Längen sind zunächst willkürlich gewählt und können für die verschiedenen Primärvalenz-Vektoren auch verschieden sein.

Um diese Willkür einzuschränken, wäre es möglich, die Primärvalenzen in photometrischen physikalischen Einheiten zu messen, beispielsweise als Vielfache der Leuchtdichteeinheit 1 cd/m². Dies führt jedoch dazu, dass unbunte Farbvalenzen Farbwerte sehr unterschiedlicher Größe haben (ein Beispiel folgt weiter unten) und wird als unpraktisch empfunden.

Stattdessen wurde festgelegt, dass eine bestimmte ausgewählte Farbvalenz durch einen Satz gleicher Farbwerte A = B = C beschrieben werden soll und die Einheiten also so gewählt, dass eine additive Mischung aus je einer Einheit der Primärvalenzen die ausgewählte Farbvalenz ergibt. Die Farbwertanteile der auf diese Weise skalierten Farbwerte sind

$\textstyle a=b=c={\frac {1}{3}}$ .

(Auf diese Weise sind nur die relativen Einheiten der Farbwerte untereinander und damit die Farbart eindeutig festgelegt. Für die absolute Skalierung dieses Farbwert-Tripels siehe den Abschnitt →Helligkeit von Licht- und Körperfarben.)

Im Prinzip könnte jede Farbart als Referenz dienen, aus praktischen Gründen sollten sie aber etwa „in der Mitte“ der möglichen Farbarten liegen. Sie werden daher aus dem Bereich der unbunten Farbarten gewählt und die Koordinaten $\textstyle a={\frac {1}{3}},b={\frac {1}{3}}$ der Farbart weiß^{[Anm.
9]} und konkret der Farbart des energiegleichen Spektrums zugeteilt.

Die Wahl des energiegleichen Spektrums als Weißpunkt darf nicht so verstanden werden, dass dieses Spektrum (das in der Natur nirgends existiert) die „weißeste Farbart“ und damit die Definition von „Weiß“ schlechthin sei. Aufgrund der eingangs erwähnten Umstimmungsfähigkeit erscheint dem Auge jede näherungsweise weiße Lichtfarbe nach kurzer Eingewöhnungsdauer als weiß. Es gibt daher kein eindeutiges weißes Licht. Werden eine Reihe näherungsweise weißer aber nicht identischer Lichtfarben angeboten, so stimmt sich das Auge auf die dominante Beleuchtung ein, empfindet diese als weiß und die anderen Lichter im Vergleich dazu als farbstichig. Stimmt sich das Auge auf eine der anderen Lichtfarben ein, so vertauschen sich die Rollen.

Historisch wurden verschiedene Lichtquellen als Weißpunkt verwendet. Die Benutzung des energiegleichen Spektrums ist jedoch aus mathematischer Sicht vorteilhaft. Sollen Farbvalenzen für eine reale Situation bestimmt werden, in der sich das Auge auf eine bestimmte Lichtart gestimmt hat (z.B. Tageslicht, Glühlampenlicht, Leuchtstoffröhrenlicht – alle von leicht unterschiedlicher Farbart), so ist die Farbtafel auf die Farbart dieser Lichtart neu zu zentrieren. Eine einfache aber meist ausreichende Methode hierfür ist die von Kries-Transformation, welche die relativen Einheiten der Primärvalenz-Vektoren neu festlegt (und damit eine „Ermüdung“ des Auges für bestimmte Primärvalenzen simuliert).

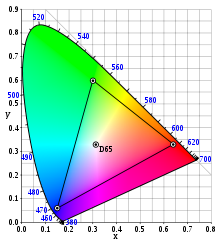
Beispielsweise hat die tageslichtähnliche Normlichtart D₆₅ in der Normfarbtafel die Farbwertanteile x = 0{,}3127 und y = 0{,}3290 , ist also im Vergleich zum energiegleichen Spektrum etwas blauer und würde von einem auf das energiegleiche Spektrum gestimmten Auge nicht als weiß gesehen, sondern als leicht bläulich. Stimmt sich das Auge um auf Beleuchtung durch D₆₅, so rückt dieses nunmehr auf den Weißpunkt a=1/3, b=1/3. Die Farbart des energiegleichen Spektrums liegt in der neu zentrierten Farbtafel nicht mehr auf dem Weißpunkt, sondern erscheint dem auf D₆₅ gestimmten Auge etwas rötlich.

Häufig benutzte Primärvalenzen

Die bisherigen Erläuterungen gelten allgemein für beliebige Primärvalenzen $\mathbf {A}$ , $\mathbf {B}$ und ${\mathbf {C}}$ . Im Folgenden werden einige häufig benutzte Primärvalenz-Tripel vorgestellt.

Instrumentelle Primärvalenzen CIE-RGB

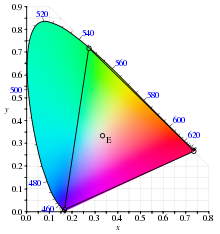
Die CIE-RGB-Spektralwertkurven ${\bar {r}}$ , ${\bar {g}}$ , ${\bar {b}}$ weisen zum Teil negative Zahlenwerte auf.

Die Lage der CIE-RGB-Primärvalenzen in der Normfarbtafel und das zugehörige Gamut-Dreieck

Frühe Messungen von Spektralwert-Funktionen wurden von J.C. Maxwell, A. König und C. Dieterici, sowie W. Abney durchgeführt. Die heutzutage als Standard benutzten Spektralwert-Funktionen gehen auf die von J. Guild und W.D. Wright um 1930 experimentell ermittelten Daten zurück. Guild (1931, 7 Versuchspersonen) und Wright (1928–1929, 10 Versuchspersonen) bestimmten Spektralwerte jeweils anhand eines 2° großen zweigeteilten Vergleichsfeldes:

Guild erzeugte die zu mischenden Primärvalenzen mit einer Wolfram-Glühlampe (Farbtemperatur 2900 K), aus deren Spektrum er mittels Filtern relativ breite rote, grüne und blaue Wellenlängenbereiche isolierte. Als Weißpunkt zur relativen Skalierung der Spektralwerte diente ein NPL-Lampennormal mit einer Farbtemperatur von etwa 4800 K.
Wright benutzte monochromatische Primärvalenzen mit den Wellenlängen 650, 530 und 460 nm. Er verwendete eine alternative Methode zur Skalierung, bestimmte jedoch die Farbwertanteile des NPL-Lampennormals bezüglich seiner Primärvalenzen, um eine Umrechnung zwischen beiden Systemen zu ermöglichen.

Ein Vergleich der beiden Datensätze – nach Umrechnung auf gleiche Primärvalenzen – zeigte trotz der unterschiedlichen Apparaturen und Verfahrensweisen eine überraschend gute Übereinstimmung, so dass ein kombinierter Datensatz als repräsentativ für den durchschnittlichen Beobachter angesehen werden konnte.

Die CIE legte 1931 Spektralwertfunktionen fest, welche das Mittel aus den Datensätzen von Guild und Wright darstellten, nachdem diese auf ebenfalls von der CIE festgelegte Primärvalenzen $\mathbf{R}$ , $\mathbf {G}$ und $\mathbf {B}$ umgerechnet worden waren. Der hypothetische Beobachter, dessen Farbrezeptoren die von diesen Spektralwert-Funktionen beschriebenen Eigenschaften haben, ist der „farbmetrische 2°-Normalbeobachter CIE 1931“.

Das CIE-RGB-System beruht auf monochromatischen Primärvalenzen mit den Wellenlängen

700,0 nm ( $\mathbf{R}$ )
546,1 nm ( $\mathbf {G}$ )
435,8 nm ( $\mathbf {B}$ ).

Die Wellenlänge 700,0 nm liegt am roten Ende des Spektrums, wo der Farbton sich nur wenig mit der Wellenlänge ändert; 546,1 und 435,8 nm sind prominente grüne bzw. violette Linien im Quecksilber spektrum, die sich also leicht und eindeutig erzeugen lassen. Die relative Skalierung der Farbwerte wurde so gewählt, dass der Farbreiz des energiegleichen Spektrums (anstelle des NPL-Weiß) untereinander gleiche Farbwertanteile $\textstyle r=g=b={\frac {1}{3}}$ hat.

Um das Weiß des energiegleichen Spektrums mit einer Leuchtdichte von 1 cd/m² zu erzeugen, werden die folgenden Leuchtdichten der additiv gemischten Primärvalenzen benötigt:^{[Anm.
10]}

$\textstyle L_{\mathbf {W} }=1\ \mathrm {\frac {cd}{m^{2}}} \quad {\begin{cases}L_{\mathbf {R} }=0{,}17697\ \mathrm {\frac {cd}{m^{2}}} \\L_{\mathbf {G} }=0{,}81240\ \mathrm {\frac {cd}{m^{2}}} \\L_{\mathbf {B} }=0{,}01063\ \mathrm {\frac {cd}{m^{2}}} \end{cases}}$

Die RGB-Primärvalenzen sind in einem Weiß also keineswegs in gleichen Leuchtdichteanteilen enthalten. Wie oben erläutert, werden aus praktischen Gründen die Einheiten für die Farbwerte so gewählt, dass

eine Einheit des Farbwerts der Leuchtdichte 0,17697 cd/m² entspricht
eine Einheit des Farbwerts der Leuchtdichte 0,81240 cd/m² entspricht
eine Einheit des Farbwerts der Leuchtdichte 0,01063 cd/m² entspricht (oder jeweils gleichen Vielfachen davon).

Für die Farbwerte des Weißpunkts gilt damit R = G = B .

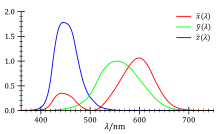
Wie das Spektralwert-Diagramm für die CIE-RGB-Primärvalenzen zeigt, haben die Spektralwerte ${\bar {r}}$ , ${\bar {g}}$ , ${\bar {b}}$ und damit die Spektralwertanteile teilweise negative Zahlenwerte. Dies liegt daran, dass das gesamte Gamut-Dreieck innerhalb des Spektralfarbenzugs liegt (mit Ausnahme der Ecken, die auf dem Spektralfarbenzug liegen). Die Spektralfarben (mit Ausnahme der drei als Primärvalenzen benutzten Spektralfarben) liegen also außerhalb des Gamuts und können nur durch äußere Mischung erzeugt werden, was das Auftreten negativer Farbwerte nach sich zieht.

Normvalenzen XYZ

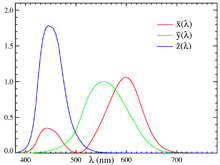
→ Hauptartikel: CIE-Normvalenzsystem

Die Normspektralwert-Funktionen ${\bar {x}}$ , $\bar{y}$ , ${\bar {z}}$ weisen keine negativen Zahlenwerte auf. Die Spektralwert-Kurve ${\bar {x}}$ besitzt neben dem Hauptmaximum ein kleines Nebenmaximum.

Die CIE führte 1931 gleichzeitig einen zweiten Satz von Spektralwert-Funktionen ${\bar {x}}$ , $\bar{y}$ , ${\bar {z}}$ ein, der sich aus dem RGB-Satz durch Umrechnung auf neue Primärvalenzen ${\mathbf {X}}$ , ${\mathbf {Y}}$ und ${\mathbf {Z}}$ ergibt und besonders bequeme Eigenschaften hat.

Positive Farbwerte

Das Auftreten negativer Spektralwerte war für die damaligen manuellen Rechnungen unbequem und sollte im XYZ-System vermieden werden. Dazu war es notwendig, die neuen Primärvalenzen ${\mathbf {X}}$ , ${\mathbf {Y}}$ und ${\mathbf {Z}}$ so zu wählen, dass das von ihnen aufgespannte Gamut-Dreieck den Spektralfarbenzug vollständig umschließt und so erlaubt, alle spektralen Farbvalenzen durch innere Mischung aus den Primärvalenzen zu erzeugen. Da die Primärvalenzen dazu außerhalb des Spektralfarbenzugs liegen müssen, sind sie notwendigerweise virtuelle Farbvalenzen und nicht physikalisch darstellbar.^{[Anm.
11]}

Im Farbraum liegen die Vektoren, welche die Primärvalenzen ${\mathbf {X}}$ , ${\mathbf {Y}}$ und ${\mathbf {Z}}$ darstellen, außerhalb des Bereichs der Vektoren, die reelle Farbvalenzen darstellen. In der -Farbtafel liegen die Farbarten der Primärvalenzen außerhalb des vom Spektralzug begrenzten Bereiches reeller Farbarten und das von ihnen gebildete Gamut-Dreieck umschließt den Bereich reeller Farbarten vollständig. Damit ist sichergestellt, dass die Farbart-Koordinaten , , und die Farbwerte , , beliebiger reeller Farbvalenzen nie negativ sind.

Y als Hellempfindlichkeitsgrad

Es erweist sich als günstig, die Information über die Leuchtdichte der Farbe von der Information über die Farbart zu trennen. Wird die Leuchtdichte nicht benötigt, muss nur mit der Farbart-Information gearbeitet werden. Wird die Leuchtdichte jedoch benötigt, steht sie unmittelbar zur Verfügung.

Für Farbvalenzen im CIE-RGB-Raum gilt das Abneysche Gesetz für die Leuchtdichte Null,

$L_R \cdot R + L_G \cdot G + L_B \cdot B = 0$

so beschreibt diese Formel jene Ebene im Farbraum, in der die Farbvalenzen die Leuchtdichte Null besitzen. Diese Ebene wird „Alychne“ (die Lichtlose) genannt. Werden Farbvalenzen aus der Alychnen-Ebene als Primärvalenzen ${\mathbf {X}}$ und ${\mathbf {Z}}$ gewählt, so besitzen sie die Leuchtdichte Null und tragen nicht zur Leuchtdichte einer betrachteten Farbvalenz bei. Die Helligkeitsinformation wird jetzt nur vom Farbwert der Primärvalenz ${\mathbf {Y}}$ getragen. Dass für diese Rolle gewählt wurde und nicht oder ist lediglich eine Konvention ohne tieferen Grund.

Es bleibt näher zu spezifizieren. Die wellenlängenabhängige Hell-Empfindlichkeit des photometrischen Normalbeobachters für Lichtreize wird durch die V(λ)-Kurve beschrieben. V(λ) kann unter sehr allgemeinen Voraussetzungen stets als Linearkombination von farbmetrischen Spektralwert-Funktionen dargestellt werden. Da die Spektralwert-Funktionen ${\bar {x}}$ , $\bar{y}$ , ${\bar {z}}$ sich bei der Transformation von $\mathbf{RGB}$ nach $\mathbf{XYZ}$ ohnehin als Linearkombinationen von ${\bar {r}}$ , ${\bar {g}}$ , ${\bar {b}}$ ergeben, lässt sich für eine von ihnen (man wählt willkürlich $\bar{y}$ ) die Linearkombination so wählen, dass gerade V(λ) resultiert:

$\bar{y}(\lambda) = V(\lambda)$

Für einen gegebenen Lichtreiz der Spektralverteilung $\varphi_{\lambda}$ ergibt sich der Farbwert als Integral über die mit der Spektralwert-Funktion gewichtete Spektralverteilung (siehe Abschnitt →Spektralwerte):

$Y = k \int \bar{y}(\lambda) \, \varphi_{\lambda} \, \mathrm{d}\lambda = k \int V(\lambda) \, \varphi_{\lambda} \, \mathrm{d}\lambda$

Dies ist gleichzeitig nichts anderes als die Formel zur Ermittlung einer photometrischen Größe aus der Spektralverteilung der zugehörigen radiometrischen Größe (siehe zum Beispiel die →Definition des Lichtstroms). Zur Wahl des Faktors siehe den Abschnitt →Helligkeit von Licht- und Körperfarben. Der durch die von der CIE festgelegten Spektralwertfunktionen definierte farbmetrische Normalbeobachter ist auf diese Weise gleichzeitig ein photometrischer Normalbeobachter.

Das Abneysche Gesetz nimmt im $\mathbf{XYZ}$ -Farbraum eine besonders einfache Gestalt an: Die Leuchtdichtebeiwerte sind

und es gilt, wie vorausgesetzt:

$L = L_X \cdot X + L_Y \cdot Y + L_Z \cdot Z = 1 \cdot Y = Y$

Weitere Eigenschaften

Weitere zur vollständigen Definition des XYZ-Raumes festgelegte Eigenschaften sind: In der -Farbtafel liegt der die Farbart von ${\mathbf {X}}$ darstellende Punkt auf der geradlinigen Verlängerung des langwelligen Endes des Spektralfarbenzugs. Die Dreiecksseite $\mathbf{ZY}$ berührt den Spektralfarbenzug. Die Lage des Farbart-Punkts von ${\mathbf {Y}}$ wird so gewählt, dass das Dreieck $\mathbf{XYZ}$ eine möglichst geringe Fläche umschließt.

Wird noch (willkürlich) festgelegt, dass das resultierende Gamut-Dreieck $\mathbf{XYZ}$ als rechtwinklig gleichschenkliges Dreieck dargestellt werden soll, ergibt sich die -Farbtafel.

Die -Achse der -Farbtafel ist die Schnittlinie der Farbtafelebene mit der Alychnenebene (sie wird deshalb gelegentlich als „Alychnen-Spur“ bezeichnet). Sie liegt außerhalb des Bereiches reeller Farbarten: reell darstellbare Farbvalenzen müssen eine Leuchtdichte besitzen, die größer als Null ist.

Normung

Die Farbmessungs-Norm DIN 5033 übernimmt die Empfehlung der CIE und sieht die Verwendung des XYZ-Farbraums zur „Farbbeschreibung von Materialien und Lichtern auf metrischer Grundlage“ vor. Die genormten Primärvalenzen ${\mathbf {X}}$ , ${\mathbf {Y}}$ , ${\mathbf {Z}}$ heißen daher auch Normvalenzen. Die Farbwerte , , heißen Normfarbwerte. Die Farbwertanteile , , heißen Normfarbwertanteile. Die Spektralwerte ${\bar {x}}$ , $\bar{y}$ , ${\bar {z}}$ heißen Normspektralwerte. Die -Farbtafel heißt Normfarbtafel.

XYZ-Koordinaten

Für die Normfarbwertanteile gilt

$\begin{align} x = \frac{X}{X + Y + Z} \\ y = \frac{Y}{X + Y + Z} \\ z = \frac{Z}{X + Y + Z} \end{align}$ ,

wobei wiederum redundant ist. und enthalten wie stets bei Farbwertanteilen nur Farb- aber keine Helligkeitsinformation. Wird der Farbwert , der Helligkeits- aber keine Farbinformation enthält, ergänzt, so ergeben sich die häufig benutzten xyY -Koordinaten. Sind , und gegeben, so errechnen sich die Farbwerte , daraus über die Formeln

$\begin{align} X = & Y \cdot \frac{x}{y} \\ Y = & Y \\ Z = & Y \cdot \frac{1-x-y}{y} \end{align}$

Transformation von CIE-RGB nach XYZ

Die Matrix zur Transformation vom CIE-RGB-System ins XYZ-Normvalenzsystem lautet:

$\begin{alignat}{4} X & \ = \ & 0{,}49 \ R & \ + \ & 0{,}31 \ G & \ + \ & 0{,}20 \ B \\ Y & \ = \ & 0{,}17697 \ R & \ + \ & 0{,}81240 \ G & \ + \ & 0{,}01063 \ B \\ Z & \ = \ & 0{,}00 \ R & \ + \ & 0{,}01 \ G & \ + \ & 0{,}99 \ B \\ \end{alignat}$

In der zweiten Zeile steht das Abneysche Gesetz mit den bereits erwähnten Leuchtdichtebeiwerten für die RGB-Primärvalenzen.

Die Zeilensummen der Matrix sind alle gleich eins. Daraus folgt insbesondere, dass im Falle gleicher R=G=B auch die X=Y=Z gleich sind. Der neue Weißpunkt ist also identisch mit dem alten Weißpunkt. Die Matrix kann so modifiziert werden, dass sie beim Primärvalenz-Wechsel gleichzeitig einen Weißpunkt-Wechsel vornimmt.

Großfeld-Normvalenzen X₁₀Y₁₀Z₁₀

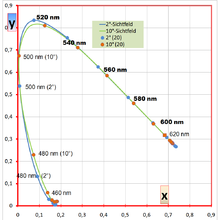
Darstellung der Spektralfarbenzüge für den 2°- und den 10°-Beobachter. Die Kurvenverläufe sind sehr ähnlich, einzelne Farbart-Punkte weisen jedoch deutlich unterschiedliche Lagen auf, vor allem im linken Kurvenast.

Die Messungen von Guild und Wright, auf denen die Normspektralwerte beruhen, wurden mit 2° großen Farbfeldern vorgenommen. Die Wahl dieser geringen Größe beruhte zum einen darauf, dass sich in dem dadurch abgedeckten Bereich der Netzhaut keine Stäbchen befinden, deren eventuelle Einmischung in den Sehvorgang aufgrund ihrer anderen spektralen Empfindlichkeit die Spektralwerte verfälscht hätte. Zum anderen ist der gelbe Fleck der Netzhaut, der als Farbfilter wirkt, in diesem zentralen Bereich relativ gleichmäßig ausgeprägt. Die CIE empfiehlt die Verwendung der Normspektralwerte des „2°-Normalbeobachters“ (siehe oben) für Farbflächen mit Ausdehnungen zwischen ein und vier Grad, in der Praxis werden sie auch für kleinere Farbflächen verwendet.

Da die meisten Sehvorgänge im Alltag größere Farbflächen betreffen, wurden später zusätzlich Spektralwert-Funktionen an größeren Farbflächen vermessen. Diese Datensätze definieren den „farbmetrischen CIE 10°-Normalbeobachter 1964“. Bei den Messungen mussten hinreichend hohe Leuchtdichten verwendet werden, um eine Beteiligung der Stäbchen zu verhindern. Da der gelbe Fleck einen Durchmesser von etwa 5° hat, beeinflusst er die Farbwahrnehmung des 10°-Beobachters weniger als die des 2°-Beobachters.

Die Konstruktionsprinzipien des X₁₀Y₁₀Z₁₀-Farbraums entsprechen denen des XYZ-Farbraums. Insbesondere gilt für die Farbwerte des energiegleichen Spektrums als Weißpunkt:

$X_{10} = Y_{10} = Z_{10}$ .

Die Hellempfindlichkeitskurve V(λ) lässt sich nicht als Linearkombination der 10°-Spektralwertkurven darstellen. Es kann also vorkommen, dass zwei Farbreize im 10°-Normvalenzsystem die gleiche Farbvalenz besitzen und dennoch – mit V(λ) gewichtet – leicht unterschiedliche Leuchtdichten besitzen; da sich die V(λ)-Kurve auf einen photometrischen 2°-Beobachter bezieht, ist dies kein physikalischer Widerspruch. Die Spektralwert-Funktion $\bar{y}_{10}$ kann als Hellempfindlichkeitskurve V₁₀(λ) für Farbflächen von etwa 10° Durchmesser interpretiert werden.

Eine Umrechnung zwischen dem farbmetrischen 2°-Normalbeobachter und dem 10°-Normalbeobachter ist nicht möglich. Es existiert jedenfalls keine lineare Transformation zwischen den beiden Systemen, da Farbreize, die in dem einen System gleichfarbig aussehen, im anderen System verschiedenfarbig aussehen können und umgekehrt. Die Daten müssen jeweils separat gemessen oder separat aus der Spektralverteilung des Farbreizes berechnet werden.

Die CIE empfiehlt die Verwendung des 10°-Normalbeobachters für Farbflächen über 4° Durchmesser.

Grundvalenzen LMS

Die Grundvalenzen ${\mathbf {L}}$ , ${\mathbf {M}}$ , $\mathbf{S}$ sind jene drei Primärvalenzen, deren zugehörige Spektralwertfunktionen identisch sind mit den wellenlängenabhängigen Empfindlichkeitskurven der drei Farbrezeptor-Arten der Netzhaut.

Da die Empfindlichkeitskurven grundsätzlich keine negativen Zahlenwerte annehmen können, müssen auch die drei Spektralwertfunktionen des LMS-Systems ausschließlich nichtnegative Werte aufweisen. Dies ist nur möglich, wenn alle Spektralfarben (und damit alle anderen reellen Farben) ausschließlich durch innere Mischung aus den Grundvalenzen ermischbar sind. Die drei Grundvalenzen müssen folglich ein den Spektralfarbenzug vollständig umschließendes Gamut-Dreieck aufspannen, selbst also außerhalb des Spektralfarbenzugs liegen. Es handelt sich daher (ähnlich wie bei den Normvalenzen) um virtuelle Primärvalenzen. Jede von ihnen entspricht jener Farbvalenz, welche die zugehörige Farbrezeptor-Art „sehen“ würde, wenn sie allein gereizt würde. Wegen der Überlappung der Empfindlichkeitsbereiche ist es jedoch nicht möglich, eine Rezeptorart allein zu reizen, und keine der Grundvalenzen kann reell erzeugt werden.

Die Grundvalenzen können ermittelt werden, indem man Farbnachstell-Experimente mit normalsichtigen und mit dichromatisch farbfehlsichtigen Probanden untereinander vergleicht; bei letzteren ist eine der Rezeptor-Arten nicht funktional.

Ein normalsichtiger Proband kann beispielsweise alle reellen Farbvalenzen unterscheiden, die sich durch variable Zumischung der Primärvalenz ${\mathbf {L}}$ (Rot) zu einer gegebenen Farbvalenz $\mathbf {F}$ erzeugen lassen. In einer -Farbtafel liegen alle diese ermischten Farbarten auf der geraden Verbindungslinie zwischen der Farbart von $\mathbf {F}$ und der Farbart von ${\mathbf {L}}$ .
Diese Unterscheidungen, die lediglich auf verschiedenen Erregungen der L-Rezeptoren beruhen, sind für einen Protanopen nicht möglich, da dessen L-Rezeptoren nicht funktional sind. Er kann alle Farben entlang der genannten Verbindungslinie nicht voneinander unterscheiden. Werden über die Farbtafel verteilt mehrere solcher Farbverwechslungsgeraden ermittelt, die sich ergeben für mehrere gegebene Farbvalenzen $\mathbf {F}$ und jeweils variable Zumischung der festen Primärvalenz ${\mathbf {L}}$ , so schneiden sich diese Geraden in einem Punkt außerhalb des Bereichs reeller Farben; dieser Punkt entspricht der Lage von ${\mathbf {L}}$ in der Farbtafel.

Entsprechend lassen sich auch die Farbkoordinaten von ${\mathbf {M}}$ und $\mathbf{S}$ experimentell ermitteln.

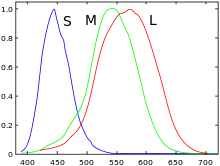
Die Grundspektralwert-Funktionen $\bar{l}$ , $\bar{m}$ , ${\bar {s}}$ sind identisch mit den spektralen Empfindlichkeitskurven der Zapfenarten L, M und S.

Die Umrechnung zwischen dem Normvalenz-Raum und dem Grundvalenz-Raum geschieht mittels folgender Matrix:

$\begin{alignat}{4} L & \ = \ & 0{,}38971 \ X & \ + \ & 0{,}68898 \ Y & \ - \ & 0{,}07868 \ Z \\ M & \ = \ & - 0{,}22981 \ X & \ + \ & 1{,}18340 \ Y & \ + \ & 0{,}04641 \ Z \\ S & \ = \ & & & & & 1{,}00000 \ Z \\ \end{alignat}$

Anwendung dieser Transformation auf die Normspektralwertfunktionen ${\bar {x}}$ , $\bar{y}$ , ${\bar {z}}$ ergibt die Grundspektralwertfunktion $\bar{l}$ , $\bar{m}$ , ${\bar {s}}$ . Diese haben weder negative Zahlenwerte noch Nebenmaxima und können als spektrale Empfindlichkeitskurven der drei Farbrezeptorarten angesehen werden.

Angewandt auf eine Farbvalenz (X, Y, Z) liefert die Transformation ein Maß für die Reizung der einzelnen Rezeptorarten L, M, S durch diese Farbvalenz. Die Skalierung ist wieder so gewählt, dass der Weißpunkt erhalten bleibt.

Statt auf die Kleinfeld-Normvalenzen ${\mathbf {X}}$ , ${\mathbf {Y}}$ , ${\mathbf {Z}}$ kann die Transformation auch auf die Großfeld-Normvalenzen $\mathbf{X_{10}}$ , $\mathbf{Y_{10}}$ , $\mathbf{Z_{10}}$ angewendet werden.

Monitor-Primärvalenzen RGB

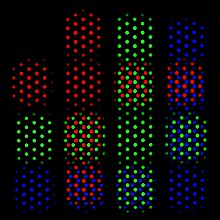
Das Bild eines Farbmonitors besteht aus Bildpunkten in drei vorgegebenen Farben.

Die Lage der sRGB-Primärvalenzen in der Normfarbtafel und das zugehörige Gamut-Dreieck.

Farbmonitore erzeugen die darzustellenden farbigen Bildinhalte durch additive Mischung der Beiträge von farbig leuchtenden Bildpunkten. Jeder Bildpunkt sendet Licht in jeweils einer von drei Farben aus, die durch den für diesen Punkt verwendeten Leuchtstoff oder Filter vorgegeben ist.

Je größer das durch die drei technisch vorgegebenen Primärvalenzen aufgespannte Gamut-Dreieck, desto größer der vom Monitor darstellbare Farbbereich. Um ein möglichst großes Dreieck zu erreichen, müssen die Primärvalenzen jeweils aus dem Bereich roter, grüner und blauer Farbvalenzen (den „Ecken“ der Farbtafel) gewählt werden. Im Interesse eines großen Gamuts sollten die Primärvalenzen möglichst Spektralfarben sein, damit sich die Ecken des Gamut-Dreiecks bis zum Spektralfarbenzug erstrecken. Entsprechende Leuchtstoffe haben jedoch nur eine geringe Leuchtkraft, da sie nur auf einem winzigen Teil des verfügbaren Spektrums leuchten dürfen. Die Wahl der Primärvalenzen ist also ein Kompromiss aus der Gamut-Größe einerseits und der Leuchtkraft sowie der technischen und kommerziellen Verfügbarkeit der Leuchtstoffe andererseits.

Ein häufig benutzter Satz von Monitor-Primärvalenzen sind die sRGB-Primärvalenzen. Ihre Norm-Farbartkoordinaten sind:

$\begin{align} \mathbf{R}: x = 0{,}64, y = 0{,}33, z = 0{,}03 \\ \mathbf{G}: x = 0{,}30, y = 0{,}60, z = 0{,}10 \\ \mathbf{B}: x = 0{,}15, y = 0{,}06, z = 0{,}79 \\ \end{align}$

Die Umrechnung vom Normvalenzsystem in das sRGB-Primärvalenzsystem geschieht mittels

$\begin{alignat}{4} R & \ = \ & 3{,}2406255 \ X_N & \ - \ & 1{,}537208 \ Y_N & \ - \ & 0{,}4986286 \ Z_N \\ G & \ = \ & -0{,}9689307 \ X_N & \ + \ & 1{,}8757561 \ Y_N & \ + \ & 0{,}0415175 \ Z_N \\ B & \ = \ & 0{,}0557101 \ X_N & \ - \ & 0{,}2040211 \ Y_N & \ + \ & 1{,}0569959 \ Z_N \\ \end{alignat}$

wobei X_N , $Y_{N}$ und Z_N normierte Normfarbwerte sind.

Helligkeit von Licht- und Körperfarben

In den Gleichungen

$\begin{align} X = k \int \bar{x}(\lambda) \, \varphi_{\lambda} \, \mathrm{d}\lambda \\ Y = k \int \bar{y}(\lambda) \, \varphi_{\lambda} \, \mathrm{d}\lambda \\ Z = k \int \bar{z}(\lambda) \, \varphi_{\lambda} \, \mathrm{d}\lambda \\ \end{align}$

ist der Faktor bislang unbestimmt geblieben. Interessieren nur die Verhältnisse der Farbwerte X, Y, Z (z.B. die Farbwertanteile x,y ), so kürzt sich dieser Faktor fort. Soll jedoch die Helligkeit des Lichtstrahls angegeben werden, so muss explizit bestimmt werden. Da die Normvalenzen so gewählt sind, dass die Helligkeitsinformation nur vom Normfarbwert getragen wird, genügt es, die Gleichung

${\begin{aligned}Y&=k\int {\bar {y}}(\lambda )\,\varphi _{\lambda }\,\mathrm {d} \lambda \\&=k\int V(\lambda )\,\varphi _{\lambda }\,\mathrm {d} \lambda \quad (*)\end{aligned}}$

zu betrachten; den Gleichungen für und wird dann derselbe resultierende Zahlenwert für zugewiesen.

Während bisher die Farbvalenz eines in das Auge fallenden Lichtstrahls der Spektralverteilung $\varphi_{\lambda}$ unabhängig von seiner Entstehung und Vorgeschichte erläutert wurde, ist es nun sinnvoll, nach der Herkunft und den Wahrnehmungsumständen des betrachteten Lichtes zu unterscheiden.

Lichtfarben

Stammt der farbmetrisch zu beschreibende Lichtstrahl direkt aus einer Lichtquelle mit der Spektralverteilung $S_{\lambda}$ , so trifft diese Spektralverteilung unverändert am Auge ein:

$\varphi_{\lambda} = S_{\lambda}$ .

Die Intensität des von einer Fläche ausgesandten Lichts wird beschrieben durch eine geeignete photometrische Größe $\Phi_\mathrm{v}$ , je nach Abstrahlgeometrie und Fragestellung beispielsweise Leuchtdichte, Lichtstärke oder Lichtstrom. Mit der entsprechenden radiometrischen Größe $\Phi_\mathrm{e}$ (beispielsweise Strahldichte, Strahlstärke, Strahlungsstrom) hängt die photometrische Größe wie folgt zusammen:

$\Phi_\mathrm{v} = K_\mathrm m \int_{0}^{\infty} V(\lambda)\ \varphi_{\lambda} \ \mathrm{d}\lambda$

mit

dem Maximalwert des photometrischen Strahlungsäquivalents $\textstyle K_\mathrm{m} = 683 \, \frac{\mathrm{lm}}{\mathrm{W}}$ bei Tagsehen
dem relativen spektralen Hellempfindlichkeitsgrad $V(\lambda )$ des Auges
der Spektralverteilung $\varphi _{\lambda }={\frac {\mathrm {d} \Phi _{\mathrm {e} }(\lambda )}{\mathrm {d} \lambda }}$ der radiometrischen Größe $\Phi_\mathrm{e}$ .

Meist wird in farbmetrischem Zusammenhang als photometrische Größe die Leuchtdichte verwendet, da sie ein unmittelbares Maß für die vom Auge wahrgenommene Helligkeit einer Fläche ist:

$L = K_\mathrm m \int_{0}^{\infty} V(\lambda)\ \varphi_{\lambda} \ \mathrm{d}\lambda$

mit der Spektralverteilung $\varphi_{\lambda}$ der gemessenen Strahldichte.

Vergleich mit der Gleichung (*) für den Normfarbwert im vorhergehenden Abschnitt zeigt, dass identisch mit der Leuchtdichte ist:

$Y = 683 \, \frac{\mathrm{lm}}{\mathrm{W}} \int V(\lambda) \, \varphi_{\lambda} \, \mathrm{d}\lambda = 683 \, \frac{\mathrm{lm}}{\mathrm{W}} \int V(\lambda) \, S_{\lambda} \, \mathrm{d}\lambda$ ,

wenn gesetzt wird:

$k = K_\mathrm{m} = 683 \, \frac{\mathrm{lm}}{\mathrm{W}}$ .

In diesem Fall kann der Umstand, dass die Normfarbwerte , , in absoluten Einheiten gegeben sind (etwa in den Leuchtdichteeinheiten cd/m²), durch Anbringen von Indizes betont werden, beispielsweise X_L , Y_L , $Z_{L}$ .

Analog kann vorgegangen werden, wenn die Lichtintensität durch andere photometrische Größen wie Lichtstärke oder Lichtstrom beschrieben wird, die Normfarbwerte tragen dann die betreffenden Einheiten.

In Fällen, in denen es nicht auf absolute Normfarbwerte ankommt oder nur relative Normfarbwerte bekannt sind, in denen aber dennoch Normfarbwerte angegeben werden sollen, kann der Normfarbwert willkürlich auf 100 gesetzt werden. Beispielsweise sind die Normlichtarten nur durch relative Spektralverteilungen definiert. Eine Angabe der Normfarbwerte und Normfarbwertanteile für die Normlichtart A würde lauten:

${\begin{alignedat}{2}X&=109{,}85\quad Y&&=100{,}0\quad Z=35{,}58\\x&=0{,}44758\quad y&&=0{,}40745\end{alignedat}}$

Körperfarben

Wird ein beleuchteter, nicht selbst leuchtender farbiger Gegenstand betrachtet, so ist die Spektralverteilung des ins Auge fallenden Lichtreizes gegeben durch:

$\varphi_{\lambda} = \beta(\lambda) \cdot S_{\lambda}$ ,

mit

dem spektralen Reflexionsvermögen $\beta (\lambda )\leq 1$ des Gegenstands
der Spektralverteilung $S_{\lambda}$ der beleuchtenden Lichtquelle.

Die ins Auge fallende Spektralverteilung wird also – anders als bei selbstleuchtenden Lichtquellen – nicht nur von den optischen Eigenschaften der Lichtquelle bestimmt, sondern auch von denen des beleuchteten Körpers, speziell vom wellenlängenabhängigen Reflexionsvermögen seiner Oberfläche.

Ist die Leuchtdichte der reflektierenden Oberfläche von Interesse (beispielsweise zur Beurteilung der Sichtbarkeit), so ist $\varphi_{\lambda}$ wie im vorhergehenden Abschnitt auszuwerten. In den meisten Fällen ist jedoch nicht die Leuchtdichte der Oberfläche von Interesse (die sowohl vom Reflexionsvermögen des Gegenstands als auch von den Eigenschaften der Lichtquelle abhängt), sondern nur das Reflexionsvermögen des Gegenstandes. Dieses ist eine (meist) unveränderliche Eigenschaft des Gegenstandes, die es erlaubt, ihn in der Umwelt zu erkennen und zu identifizieren.

Das Auge^{[Anm.
12]} besitzt die Fähigkeit, automatisch die Eigenschaften der Gegenstände von denen der Beleuchtung zu trennen. Wid beispielsweise die Beleuchtungsstärke einer Szene halbiert, so halbiert sich die Leuchtdichte aller Oberflächen, aber das Auge nimmt z.B. einen weißen Gegenstand jetzt nicht als grau wahr, sondern nach wie vor als weiß. Das Auge vergleicht nämlich die Gegenstände der gesamten Szene untereinander und „rechnet“ eine allen gemeinsame Helligkeitsänderung fast vollständig heraus (Helligkeitskonstanz). Unter „Helligkeit“ ist in diesem Zusammenhang also nicht eine Aussage über eine „Menge an Licht“ zu verstehen, sondern eine Aussage über ein mehr oder weniger starkes Reflexionsvermögen der Oberfläche (beispielsweise über eine „helle“ Vase im Gegensatz zu einer „dunklen“).

Soll also die Helligkeit einer Oberfläche als von der Beleuchtung unabhängige Gegenstandseigenschaft ermittelt werden, so ist die Wahrnehmung des Auges nachzuahmen, indem diese Oberfläche mit einer identisch beleuchten weißen Oberfläche ( $\beta(\lambda) = 1$ ) verglichen wird. Dieser Vergleich wird ausgedrückt durch den Hellbezugswert A, d.h. das Verhältnis der Lichtintensitäten, die von der betrachteten und von der weißen Oberfläche reflektiert werden:

$A=100\cdot {\frac {\int V(\lambda )\ \beta (\lambda )S_{\lambda }\ \mathrm {d} \lambda }{\int V(\lambda )\ S_{\lambda }\ \mathrm {d} \lambda }}\leq 100$ ^{[Anm.
13]}

(Der Faktor 100 berücksichtigt, dass der Hellbezugswert gemäß Konvention maximal den Wert 100 annehmen soll.)

Vergleich mit der Gleichung für den Normfarbwert

$Y=k\int V(\lambda )\ \beta (\lambda )S_{\lambda }\ \mathrm {d} \lambda$

zeigt, dass identisch mit dem Hellbezugswert wird, wenn der Faktor auf

$k={\frac {100}{\int V(\lambda )\ S_{\lambda }\,\mathrm {d} \lambda }}$

gesetzt wird.

Während die Helligkeit (im Sinne der Leuchtdichte) von Lichtfarben im Prinzip unbegrenzt ist und die Gesamtheit aller möglichen Lichtfarben daher im Farbraum eine ins Unendliche ausgedehnte „Farbtüte“ bildet, bleibt die Helligkeit (im Sinne des Hellbezugswertes) von Körperfarben auf maximal 100 beschränkt und wird durch einen endlichen Farbkörper im Farbraum dargestellt.

Unbezogene und bezogene Farben

Ob zur Helligkeitsangabe in einem gegebenen Fall Licht- oder Körperfarben sinnvoll sind, richtet sich genau genommen danach, wie eine farbige Fläche wahrgenommen wird:

als „unbezogene Farbe“, d.h. für sich allein stehend oder
als „bezogene Farbe“, d.h. im Zusammenhang mit anderen farbigen Flächen.

Farben von hellen Lichtquellen (Lichtfarben) werden meist als unbezogene Farben wahrgenommen, dagegen Farben von Gegenständen (Körperfarben) meist als bezogene Farben.

Ausnahmen:

gleichförmige Flächen, die vor einem unbeleuchteten Hintergrund gesehen werden, werden in der Regel als unbezogene Farben wahrgenommen, auch wenn es sich um beleuchtete statt selbstleuchtende Flächen handelt.
Bildschirmdarstellungen einer Szene bestehen zwar aus selbstleuchtenden Farbflächen, werden jedoch in der Regel als bezogene Farben wahrgenommen, sofern sie eine Ansammlung von Gegenständen darstellen.

Ausblick

Die Farbmetrik behandelt die Eigenschaften der Farbvalenzen und damit die Eigenschaften der physikalisch vorhandenen Farbreize.
Die Erfassung dieser Farbreize durch die Farbrezeptoren des Auges, die Vorverarbeitung dieser Reize in den Nervenzellen der Netzhaut, ihre Umcodierung und Weiterleitung im Sehnerv sowie ihre Verarbeitung im visuellen Cortex des Gehirns sind komplexe psychophysische Vorgänge, an deren Ende die Farbwahrnehmung steht. Die Farbwahrnehmung mit ihrer Abhängigkeit von den Beobachtungsbedingungen sowie ihren Kontrast- und Nachwirkungseffekten unterliegt wesentlich komplexeren Gesetzen als die Farbmetrik. Begriffe wie Farbton, Farbsättigung oder Helligkeit beschreiben Eigenschaften einer wahrgenommenen Farbe, keine Eigenschaften einer Farbvalenz.^{[Anm.
14]}
Beispielsweise wird die „Intensität“ einer Farbvalenz durch ihre Leuchtdichte beschrieben, jedoch ist die Helligkeit der entsprechenden wahrgenommenen Farbe nicht proportional zur Leuchtdichte der auslösenden Farbvalenz. Leuchtdichten verhalten sich additiv (d.h. die Leuchtdichte der additiven Mischung zweier Farbvalenzen ist die Summe der Leuchtdichten der Ausgangsvalenzen), Helligkeiten dagegen sind nicht additiv. Die wahrgenommene Helligkeit einer Farbe steigt mit zunehmender Farbsättigung, auch wenn die Leuchtdichte der Farbvalenz, welche die Wahrnehmung auslöst, konstant bleibt. (Helmholtz-Kohlrausch-Effekt)
Die folgende Tabelle stellt einige Maßgrößen für Farbvalenzen den entsprechenden Maßgrößen für wahrgenommene Farben gegenüber. Der Zusammenhang zwischen beiden kann sehr komplex sein.

Farbvalenz	wahrgenommene Farbe
Leuchtdichte	Helligkeit (einer unbezogenen Farbe)
Hellbezugswert $A = L/L_{\text{Bezugsweiß}}$	Helligkeit (einer bezogenen Farbe)
Farbart	Farbton und Sättigung
bunttongleiche Wellenlänge $\lambda_\mathrm{d}$	Farbton
spektraler Farbanteil $p_\mathrm{e}$	Sättigung

Neben unterschiedlichen Primärvalenzen können auch verschiedene Geometrien zur Darstellung der Gesamtheit der Farbörter verwendet werden, darauf beruhen die verschiedenen Farbräume. Diese hängen teilweise nichtlinear mit dem Normvalenz-Raum zusammen, aber stets werden genau drei Farbkoordinaten benötigt.
Beispielsweise sind im Farbsystem von Munsell die Koordinaten Hue, Value und Chroma, wobei die Farbörter in einem Kugelkoordinatensystem beschrieben sind.
Im L*a*b*-Farbraum wird die Farbvalenz bestimmt als {L*,a*,b*} mit Helligkeit (L*), rot-grün-Wert (a*), blau-gelb-Wert (b*). Die L*-Koordinate versucht den nichtlinearen Zusammenhang zwischen Leuchtdichte und Helligkeit näherungsweise nachzubilden.
Die Anordnung der Farbarten in Farbtafeln erlaubt es, die Zusammenhänge der Farbarten bei additiver Mischung zu überblicken. In der Normfarbtafel sind die Farbarten jedoch nicht „empfindungsgemäß gleichabständig“ angeordnet. Werden beispielsweise zwei grüne Farbarten vom Beobachter als „in gleichem Maße verschieden“ empfunden wie zwei gegebene rote Farbarten, so sind in der Normfarbtafel die beiden grünen Farbarten deutlich weiter voneinander entfernt als die roten. Aus dem Abstand zweier Farbarten in der Normfarbtafel lässt sich also nicht auf ihre wahrgenommene Ähnlichkeit schließen. Farbräume wie CIELUV oder CIELAB sollen dieses Problem mindern.

Der Zusammenhang der Begriffe Farbreiz, Farbvalenz und Farbempfindung
Begriff	Wirkort	Wirkart	Fachgebiet
Farbreiz	Lichtquelle	Transport von Photonen	Entstehung von Farben / Optik
Farbvalenz	Auge (Zapfen)	Spektralspezifische Reaktion der Netzhaut	Optik + Physiologie
Farbempfindung	Gehirn	Farbwahrnehmung	Physiologie / Psychologie

Literatur

M. Richter: Einführung in die Farbmetrik. 2. Auflage, Walter de Gruyter, Berlin / New York 1981, ISBN 3-11-008209-8
H. Lang: Farbmetrik. In: Bergmann-Schaefer: Lehrbuch der Experimentalphysik. Band 3: Optik. 10. Auflage, Walter de Gruyter, Berlin / New York 2004, ISBN 3-11-017081-7
R.W.G. Hunt: Measuring Colour. 3rd ed., Fountain Press, Kingston-upon-Thames 1998, ISBN 0-86343-387-1
G. Wyszecki, W.S. Stiles: Color Science – Concepts and Methods, Quantitative Data and Formulae. 2nd ed., John Wiley & Sons 1982, ISBN 0-471-02106-7 (Wiley Classics Library Edition, 2000: ISBN 0-471-39918-3)

Anmerkungen

↑ Die möglichen Spektralverteilungen bilden eine unendlich-dimensionale Mannigfaltigkeit, die möglichen Farbwahrnehmungen bilden nur eine dreidimensionale Mannigfaltigkeit. Bei der Farbwahrnehmung werden zwangsläufig stets unendlich viele Spektral-Vektoren auf einen Farbvalenz-Vektor abgebildet.
Dies ist nicht zu verwechseln mit dem Umstand, dass das Auge ein begrenztes Farbunterscheidungsvermögen besitzt, dass also sehr ähnliche Farben vom Auge unter Umständen nicht unterschieden werden können und deshalb als gleich wahrgenommen werden.
↑ Da die Empfindlichkeitsbereiche der drei Rezeptorarten einander größtenteils überlagern, lösen die beiden als Beispiel genannten Lichtstrahlen in mindestens einer der beiden anderen Rezeptorarten ebenfalls Reize aus, hier aber in der Regel Reize anderer Stärke. Das Verhältnis der Reizstärken, die ein monochromatischer Lichtstrahl in zwei verschiedenen Rezeptorarten auslöst, erlaubt Rückschlüsse auf die Lage der Lichtwellenlänge im gemeinsamen Empfindlichkeitsbereich, bleibt aber bei einer Änderung der Lichtreizintensität unverändert. Auf diesem Umstand beruht die Fähigkeit des Auges, Farbinformation getrennt von Helligkeitsinformation wahrnehmen zu können.
Die dem Nachtsehen dienenden Stäbchen haben einen ähnlichen Empfindlichkeitsbereich wie jeder der Farbrezeptoren, können aber keine Differenzen zu anderen Stäbchenarten bilden. Sie liefern Helligkeits-, aber keine Farbwahrnehmung.
↑ Das bedeutet nicht, dass metamere Farben unter allen Umständen gleich aussehen. Bei metameren Körperfarben kann schon ein Wechsel der beleuchtenden Lichtart die Gleichheit zerstören; Farben, die für einen 2°-Beobachter metamer sind, müssen es für einen 10°-Beobachter nicht unbedingt sein; usw.
↑ Für die additive Mischung lässt sich also beispielsweise die allgemein gültige Regel aufstellen: „Grün gemischt mit Rot ergibt Gelb“, ohne dass Rücksicht darauf zu nehmen ist, welche Spektralverteilungen diese Farbreize haben.
Für andere Arten der Farbmischung gibt es solche Regeln im Allgemeinen nicht. Für die subtraktive Farbmischung beispielsweise wird oft die Regel „Blau subtraktiv mit Gelb gemischt ergibt Grün“ gelehrt. Damit ist gemeint, dass von weißem Licht, von dem ein Blaufilter den langwelligen Anteil und ein Gelbfilter den kurzwelligen Anteil entfernt haben, nur die mittleren Wellenlängen übrigbleiben, das Mischungsergebnis also grün aussieht. Das gilt aber nur, wenn sowohl der Blau- als auch der Gelbfilter die grünen Wellenlängen durchlassen, beide also einen gemeinsamen Durchlassbereich haben. Überschneiden sich ihre Durchlassbereiche nicht, dann gibt es kein Licht, das beide Filter passieren kann, und das Mischungsergebnis ist Schwarz. Es kommt hier also nicht allein darauf an, dass ein Filter blau und einer gelb aussieht, auch ihre Spektralverteilungen müssen berücksichtigt werden.
↑ Für ein voll farbtüchtiges, also trichromatisches menschliches Auge.
↑ Die Farbart ist bestimmt durch den „Farbton“ und die „Farbsättigung“. (Diese hier der Anschaulichkeit halber benutzten Begriffe stehen in Anführungszeichen, weil sie eigentlich Eigenschaften der Farbwahrnehmung beschreiben und nicht die hier behandelten Eigenschaften der physikalischen Farbarten. Die korrekten Begriffe wären „bunttongleiche Wellenlänge“ und „spektraler Farbanteil“.)
↑ Photometrische Größen sind ein quantitatives Maß für einen „Lichtreiz“. Ähnlich dem Farbreiz (nur ohne Berücksichtigung der Farbeigenschaften) ist der Lichtreiz die physikalisch vorhandene Strahlung, die ins Auge tritt. Ihre quantitativen Eigenschaften sind objektiv messbar und dürfen nicht verwechselt werden mit wahrgenommenen Eigenschaften wie der Helligkeit, die in der Regel nichtlinear mit den photometrischen Eigenschaften des Lichtreizes zusammenhängen.
↑ Es handelt sich um eine Verteilungsdichte: $\textstyle \varphi_{\lambda} := \frac{\mathrm{d}\varphi(\lambda)}{\mathrm{d}\lambda}$ und damit $\textstyle \mathrm{d}\varphi(\lambda) = \varphi_{\lambda} \ \mathrm{d}\lambda$ . Dabei ist $\varphi(\lambda)$ eine für die jeweilige Mess-Situation geeignete radiometrische Größe (beispielsweise Strahldichte, Strahlstärke oder Strahlungsstrom).
↑ Da die Farbarten keine Information über die Helligkeit enthalten, sollte die als Referenz gewählte Farbart eigentlich korrekt als „unbunt“ und der Punkt a = 1/3, b = 1/3 in der Farbtafel als „Unbuntpunkt“ bezeichnet werden. Es ist aber in diesem Zusammenhang meist üblich, von der Farbart „weiß“ und dem „Weißpunkt“ zu sprechen.
↑ Diese Zahlenwerte sind auch die Leuchtdichtebeiwerte des Abneyschen Gesetzes im RGB-Raum. Allgemein gilt also für eine Leuchtdichte :

$L = L_R \cdot R + L_G \cdot G + L_B \cdot B$ .
↑ Da virtuelle Farbvalenzen grundsätzlich nicht sichtbar sein können, ist es nicht sinnvoll, sie mit Farbvokabular wie „rot“ oder „grün“ zu beschreiben. Formal jedoch entspricht ${\mathbf {X}}$ gemäß seiner Lage in der Farbtafel einer rötlichen Farbvalenz, die gesättigter ist als jedes sichtbare Rot. ${\mathbf {Y}}$ entspricht einem Grün mit dem Farbton der Spektralfarbe mit der Wellenlänge 520 nm, ist aber wesentlich gesättigter als jedes sichtbare Grün dieses Farbtons. ${\mathbf {Z}}$ entspricht einem Blau mit dem Farbton der Spektralfarbe mit der Wellenlänge 477 nm, ist aber wesentlich gesättigter als jedes sichtbare Blau dieses Farbtons (vgl. MacAdam, Color Measurement, S. 12).
↑ Die komplexen Verarbeitungsmechanismen, die für diese Wahrnehmungsleistung nötig sind, laufen größtenteils nicht im Auge selbst ab. Der Begriff „Auge“ ist hier nur als Kürzel für den gesamten beteiligten Wahrnehmungsapparat gebraucht.
↑ Im Falle lumineszenter Oberflächen kann der Hellbezugswert auch größer als 100 werden.
↑ Dennoch wird der Kürze halber, aber eigentlich unrichtig, oft von der „Helligkeit einer Farbvalenz“ gesprochen – so auch in diesem Artikel.

Basierend auf einem Artikel in:

Wikipedia.de

Farbvalenz

Erläuterung

Farbvalenz und Spektralverteilung

Farbvalenz und Farbwahrnehmung

Eigenschaften

Additive Farbmischung

Vektoren

Basisvektoren und Vektorkomponenten

Vektoraddition

Multiplikation mit einer Zahl

Basiswechsel

Farbvalenzen als Vektoren

Farbwert

Farbart

Primärvalenzen

Wechsel der Primärvalenzen

Abneysches Gesetz

Messung

Farbwertanteile und Farbtafeln

Innere und äußere Mischung

Innere Mischung

Äußere Mischung

Spektralwerte

Energiegleiches Spektrum und Farbgleichung

Spektralwerte

Spektralfarbenzug und virtuelle Farben

Reelle Farben

Virtuelle Farben

Skalierung und Weißpunkt

Häufig benutzte Primärvalenzen

Instrumentelle Primärvalenzen CIE-RGB

Normvalenzen XYZ

Positive Farbwerte

Y als Hellempfindlichkeitsgrad

Weitere Eigenschaften

Normung

XYZ-Koordinaten

Transformation von CIE-RGB nach XYZ

Großfeld-Normvalenzen X10Y10Z10

Grundvalenzen LMS

Monitor-Primärvalenzen RGB

Helligkeit von Licht- und Körperfarben

Lichtfarben

Körperfarben

Unbezogene und bezogene Farben

Ausblick

Literatur

Anmerkungen

Großfeld-Normvalenzen X₁₀Y₁₀Z₁₀