Lab-Farbraum

Der L*a*b*-Farbraum (auch: CIELAB, CIEL*a*b*, Lab-Farben) beschreibt alle wahrnehmbaren Farben. Er nutzt einen dreidimensionalen Farbenraum, bei dem der Helligkeitswert L* senkrecht auf der Farbebene (a*,b*) steht.
In Analogie zur Gegenfarbtheorie von Ewald Hering gibt die a-Koordinate die Farbart und Farbintensität zwischen Grün und Rot an und die b-Koordinate die Farbart und die Farbintensität zwischen Blau und Gelb. Je größer positive a- und b- und je kleiner negative a- und b-Werte, umso intensiver der Farbton. Falls a=0 und b=0, liegt ein unbunter Farbton auf der Helligkeitsachse vor. In den üblichen Softwareumsetzungen kann L (Lightness, Helligkeit) Werte zwischen 0 und 100 annehmen und a und b können zwischen −128 und 127 variiert werden. Im üblichen 8-Bit Modell je Farbkanal erreicht man auf diese Weise 16,7 Millionen mögliche Lab-Koordinaten. Der wirkliche Lab-Farbraum (unsere Farbwahrnehmung) geht in Teilbereichen über die genannten a/b-Grenzen hinaus und erreicht in den meisten Bereichen die genannten a/b-Grenzen nicht.
Zu den wichtigsten Eigenschaften des L*a*b*-Farbmodells zählen die Geräteunabhängigkeit und die Wahrnehmungsbezogenheit, das heißt: Farben werden unabhängig von der Art ihrer Erzeugung oder Wiedergabetechnik so definiert, wie sie von einem Normalbeobachter bei einer Standard-Lichtbedingung wahrgenommen werden.
Grundlagen
Das Farbmodell ist in der ISO/CIE 11664-4 „Colorimetry – Part 4: CIE 1976 L*a*b* Colour space“ genormt. Diese ersetzt in Deutschland die 2011 zurückgezogene DIN 6174 „Farbmetrische Bestimmung von Farbmaßzahlen und Farbabständen im angenähert gleichförmigen CIELAB-Farbenraum“.
CIE-XYZ-Farbraum
Das CIELAB-Farbsystem geht aus dem CIE-XYZ-Modell der CIE von 1931 hervor, das die drei spektralen Eigenschaften (Intensitätsverläufe im Wellenlängenbereich 380-760 nm) der Lichtart, des standardisierten Normalbeobachters und der Remissionseigenschaften der Farbprobe zu den „Farbvalenzen“ (XYZ) miteinander verrechnet. Diese Farbvalenzen beschreiben die Stärke der Intensität der Reizung der drei Farbrezeptorentypen mit den Werten X, Y und Z. Die grafische Darstellung des Tristimulusmodells der CIE ist auch bekannt als „CIE-Schuhsohle“. Es fand weite Verbreitung, erwies sich aber als unpraktisch für die Bewertung von Farbunterschieden.
| |||
| Titel | Farbmetrik – Teil 4: CIE 1976 L*a*b* Farbraum | ||
| Erstveröffentlichung | 7. November 2008 | ||
| Letzte Ausgabe | 19. Juni 2019 | ||
| Klassifikation | 17.180.20 | ||
| Nationale Normen | EN ISO/CIE 11664-4:2019-10; DIN EN ISO/CIE 11664-4:2020-03; OENORM EN ISO/CIE 11664-4:2020-01-15; SN EN ISO/CIE 11664-4:2020-02 | ||
| Ersatz für | DIN 6174 | ||
Hunter Lab-Farbraum
Der Farbraum, der 1948 von Richard Sewall Hunter definiert wurde[1][2], ist ein Farbraum, der ebenfalls als „Lab“ bezeichnet wird. Wie CIELAB wurde er so entworfen, dass Farbwerte mit einfachen Formeln aus dem CIEXYZ-Raum überführt werden können, aber bzgl. der Wahrnehmung gleichförmiger ist als XYZ. Hunter nannte seine Koordinaten L, a und b. Die Koordinaten des CIELAB-Farbraums von 1976 wurden mit L*, a* und b* bezeichnet, um sie von den Hunter-Koordinaten zu unterscheiden.

CIELAB-Farbraum
Im Farbmodell der Internationalen Beleuchtungskommission, dem CIELAB-Modell von 1976, werden die XYZ-Koordinaten einer rechnerischen Transformation unterzogen, um Bereiche gleichartiger Farbunterschiede um jede Farbraum-Koordinate zu Kreisen zu normieren. Die sogenannten MacAdam-Ellipsen, als Areale gleich stark empfundener Farbkontraste im XYZ-Raum, waren unregelmäßig geformt. Damit sollten die euklidischen Abstände gleichwertiger Unterschiede in der Farbempfindung auch mathematisch besser dargestellt werden.
Aufgrund der angestrebten Gleichabständigkeit beschreibt CIELAB unsere Farbempfindung besser als das Tristimulusmodell (CIE-XYZ). Aufgrund der Einbeziehung der Wahrnehmungskomponente (dem Normalbeobachter) beschreibt es die Farbempfindung besser als RGB, CMYK, HSB oder andere verbreitete mathematische Farbmodelle. Im Gegensatz zu diesen beschreibt es alle Farben, nicht nur die in einer bestimmten Technik darstellbaren Farbraum-Ausschnitte (Gamuts). Als mathematisches Farbmodell ist CIELAB gemeinfrei und in jeder Hinsicht frei verwendbar.
Die Gleichabständigkeit wird erreicht, indem für die Helligkeit (Luminanz L*) ein Term verwendet wird, der die dritte Wurzel des Quotienten aus dem Tristimuluswert Y und dem Weißpunkt Yn beinhaltet. Dieser Term dient dazu, die logarithmische Helligkeitswahrnehmung des menschlichen Sehapparates nachzuahmen. Eine derartige Nichtlinearität fließt auch in die Werte a* und b* bzw. u* und v* ein. Die nichtlineare Transformation ist umkehrbar.
Koordinatensystem des Farbraums

Jede Farbe im Farbraum ist durch einen Farbort mit den kartesischen Koordinaten {L*, a*, b*} definiert. Die a*b*-Koordinatenebene wurde in Anwendung der Gegenfarbentheorie konstruiert. Auf der a*-Achse liegen sich Grün und Rot gegenüber, die b*-Achse verläuft zwischen Blau und Gelb. Komplementäre Farbtöne stehen sich jeweils um 180° gegenüber, in ihrer Mitte (dem Koordinatenursprung a*=0, b*=0) ist Grau.
Die L*-Achse beschreibt die Helligkeit (Luminanz) der Farbe mit Werten von 0 bis 100. In der Darstellung steht diese im Nullpunkt senkrecht auf der a*b*-Ebene. Sie kann auch als Neutralgrauachse bezeichnet werden, denn zwischen den Endpunkten Schwarz (L*=0) und Weiß (L*=100) sind alle unbunten Farben (Grautöne) enthalten. Die a*-Achse beschreibt den Grün- oder Rotanteil einer Farbe, wobei negative Werte für Grün und positive Werte für Rot stehen. Die b*-Achse beschreibt den Blau- oder Gelbanteil einer Farbe, wobei negative Werte für Blau und positive Werte für Gelb stehen.
Die a*-Werte reichen von ca. −170 bis +100, die b*-Werte von −100 bis +150, wobei die Maximalwerte nur bei mittlerer Helligkeit bestimmter Farbtöne erreicht werden. Der CIELAB-Farbkörper hat im mittleren Helligkeitsbereich seine größte Ausdehnung, diese ist aber je nach Farbbereich unterschiedlich in Höhe und Größe. Insgesamt ist der CIELAB-Farbkörper sehr ungleichförmig – siehe Abbildungen.
Bedeutung und Verbesserungen
Das CIELAB-Farbmodell fand weltweite Verbreitung in allen Bereichen der industriellen Farbpraxis. Farbmessgeräte zeigen üblicherweise L*a*b*-Farbwerte an, in gebräuchlichen Gestaltungsprogrammen (Adobe CC, Corel GS, GIMP und anderen) kann man CIELAB-Farbwerte direkt eingeben, Farbdifferenzen werden üblicherweise als Euklidischer Abstand der L*a*b*-Werte zweier Farben berechnet und kommuniziert (ΔE).
Im Laufe der Zeit wurden von der CIE weiter verbesserte Farbdifferenzformeln entwickelt, die die Abhängigkeit einer Farbdifferenz vom Farbort und den Betrachtungsbedingungen besser berücksichtigen (ΔE 94, ΔE CMC, ΔE 2000). Diese weiteren Rechenoperationen auf die L*a*b*-Farbwerte können als weitere Verzerrung des CIELAB-Körpers aufgefasst werden, welcher damit unsere Farbwahrnehmung noch besser beschreibt.
CIELAB als geräteunabhängige Farbreferenz

Der L*a*b*-Farbraum enthält alle Farben in geräteunabhängiger Form. Er erlaubt daher die verlustfreie Konvertierung von Farbinformationen aus einem Farbsystem in ein anderes, von einer Geräteart in eine andere.
Bildbearbeitungssoftware wie Adobe Photoshop verwenden zur Umrechnung L*a*b* als Referenzfarbsystem. Mittels sogenannter ICC-Profile, in denen eine Tabelle mit einem L*a*b*-Soll/Ist-Vergleich festgelegter Farben hinterlegt ist, kann die Ausgabe von Bilddateien von einem Farbraum in einen anderen oder von einem Ausgabegerät zu einem anderen angepasst werden. So lassen sich z.B. in sRGB angelegte Bilddateien für einen spezifischen RGB-Monitor und Drucker aufbereiten oder in das zum Ausdrucken benötigte CMYK-System umwandeln, beispielsweise als „FOGRA 39“ für den Offsetdruck.
- L*a*b*-Koordinaten werden als Austauschformat zwischen unterschiedlichen Geräten eingesetzt.
- L*a*b* ist das interne Farbmodell von PostScript Level II.
Vor- und Nachteile
Das CIELAB-Modell bietet starke Vorteile gegenüber anderen mathematischen oder herstellerseitig fest definierten Systemen.
- Freie Berechenbarkeit: Die mathematische Definition ermöglicht die freie, stufenlose Berechnung von Farbe und Konvertierung in andere Farbräume.
- Eindeutige Kommunikation: Angaben wie „Lab 20 30 40“ oder „HLC 240 40 22“ sind weltweit eindeutig. Sie können an jedem Computer sichtbar gemacht werden. Im Gegensatz hierzu werden für Angaben wie Himmelblau stets definierende Ur-Muster benötigt.
- Wahrnehmungsbezogenheit: Aufgrund der angestrebten visuell-rechnerischen Gleichabständigkeit beschreibt CIELAB unsere Farbempfindung besser als das Tristimulusmodell (CIE-XYZ). Aufgrund der Einbeziehung der Wahrnehmungskomponente (dem Normalbeobachter) beschreibt es die Farbempfindung besser als RGB, HSB, CMYK oder andere verbreitete mathematische Farbmodelle.
- Alle Farben: Im Gegensatz zu anderen Modellen definiert CIELAB alle Farben eindeutig, auch solche außerhalb der Gamuts von Ausgabeverfahren. Farbkonvertierungen in CIELAB geschehen verlustfrei.
- kein kommerzielles Interesse: Die CIE als gemeinnütziger wissenschaftlicher Verein verfolgt in erster Linie Qualitätsinteressen.
- Urheber- und lizenzfrei: Als mathematisch definiertes Farbmodell ist CIELAB gemeinfrei, d.h. in jeder Hinsicht frei verwendbar und integrierbar (auch systematische Lab/HLC-Farbwertetabellen).
- Weltweite Verbreitung: Das Modell ist heute weltweiter Standard bei der Farbmessung sowie in die Farbauswahl einiger Gestaltungsprogramme (Adobe Creative Cloud, Corel, GIMP u.a.) integriert.
Nachteile des Modells lassen Verbesserungsbedarf erkennen.
- Dünne Datenbasis: Die Definition der MacAdam-Ellipsen, dem theoretischen Hintergrund der angestrebten Gleichabständigkeit, geschah auf Datenbasis weniger (einzelner) Probanden, ist statistisch nicht signifikant.
- Keine verbindlichen Farbmuster: Es existieren derzeit keine systematisch-lückenfreien CIELAB-Farbmuster, deren Genauigkeit den Anforderungen der Industrie genügt.
- Schwer verständlich (Lab): Es fällt auch dem versierten Anwender schwer, sich eine Angabe wie „Lab 20 30 40“ konkret als Farbton vorzustellen. (Die CIELAB-Polarkoordinaten HLC sind hingegen leichter verständlich: Schnelle Farbauswahl gemäß „Farbton-Helligkeit-Sättigung“.)
- Unübersichtlicher Farbraum. Je nach Farbbereich sind die Ausprägungen in Helligkeit und Chromazität sehr unterschiedlich. Der Farbraum ist in seiner Gesamtheit im Gegensatz zu einfachen geometrischen Modellen nicht intuitiv erfassbar (hierin spiegelt sich auch die Ungleichförmigkeit unserer Wahrnehmung wider).
- Lückenhafte Softwareintegration: Die Lab-Farbauswahl ist nicht in zahlreichen Softwares implementiert, stets können verwirrenderweise auch Nicht-Farben erzeugt werden und die einfach verständlichen Farbwerte LCh/HLC lassen sich nur in wenigen Nischenprodukten eingeben.
Koordinaten-Transformation
Farbvalenzen XYZ

Nach Rösch (1928) ist der CIE-XYZ-Farbraum ein dreidimensionaler Raum, bei dem immer kleinere hufeisenförmige Gebilde sich nach oben zum Weißpunkt hin verjüngen. Um der damals wenig praktikablen Dreidimensionalität der Darstellung aus dem Wege zu gehen, hat man bezüglich der grafischen Darstellung eine einfache Lösung gefunden: Man setzt den gesamten Farbeindruck stets gleich 100 %, unabhängig ob die Farbe hell oder dunkel oder stark gesättigt ist. Sodann lassen sich die einzelnen Normfarbwerte (xyz) als Anteil an der Gesamtfarbe (Farbvalenz) angeben. Damit lassen sich alle Farben in einem zweidimensionalen xy-Diagramm (da z=1-x-y) unterbringen, als „Normfarbtafel“ bezeichnet oder als „CIE-Schuhsohle“ (englisch „horseshoe“/Hufeisen) bekannt. Hierin sind alle Farben enthalten, die Darstellung der „Schuhsohle“ ist jedoch stets auf die jeweiligen farbtechnischen Möglichkeiten des Ausgabeverfahrens, den „Gamut“ beschränkt. Anzumerken ist deshalb, dass daher in der nebenstehenden Abbildung der „Schuhsohle“ der außerhalb des sRGB-Dreiecks liegende Bereich zu wenig gesättigt gezeigt wird.
Der äußere obere Kurvenzug der Schuhsohle repräsentiert die Spektralfarben, welche die maximal erreichbaren Farbintensitäten darstellen. Bei ihnen herrscht maximales Licht in einem einzigen Wellenlängenintervall sowie kein Licht in den anderen. In der unteren geraden Verbindung, der „Purpurgerade“, fallen maximale Intensitäten des Spektrum-Anfangs und -Endes zusammen. Die enge Verwandtschaft des Spektralfarbenzugs zum CIEL*a*b*-Farbkreis ist erkennbar.
- Darstellung L*, a*, b* abhängig von der Wellenlänge
-
![Luminanz L*[3]](bilder/255px-L-versus-Lambda.png) Luminanz L*[3]
Luminanz L*[3] -
![Grün-Rot-Parameter a*[3]](bilder/264px-A_versus_Wellenlaenge.png) Grün-Rot-Parameter a*[3]
Grün-Rot-Parameter a*[3] -
![Blau-Gelb-Parameter b*[3]](bilder/239px-B_versus_Wellenlaenge.png) Blau-Gelb-Parameter b*[3]
Blau-Gelb-Parameter b*[3] -
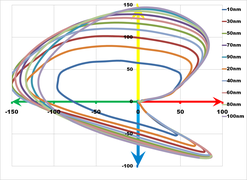 Diagramm der a*/b*-Ebene.
Diagramm der a*/b*-Ebene.
Der XYZ-Farbraum ist nicht perzeptiv gleichabständig. Der zahlenmäßig gleiche Farbabstand zwischen zwei Farbörtern wird nicht im gesamten Farbkörper als gleichartiger Farbunterschied wahrgenommen. Daher ist der XYZ-Farbraum als universelle Metrik, analog dem Metermaß aus dem Längenbereich, ungeeignet. Für das L*a*b*-Farbmodell wird der XYZ-Farbraum durch mathematische Transformationen wahrnehmungsgerecht verzerrt, um diesen Nachteil zu überwinden.
Umrechnung von XYZ zu Lab
Je nach Beobachterwinkel und Lichtart sind unterschiedliche Normvalenzen bei der Berechnung zu berücksichtigen. Der Beobachterwinkel von 2° entspricht dem CIE-Normalbeobachter von 1931, der Winkel von 10° entspricht dem CIE-Normalbeobachter von 1976. Die 2° ergaben sich aus der Fläche der besten Farbensicht im Auge, 10° gelten als Blickwinkel eines A4-Blattes in (üblichem) Betrachtungsabstand. Im amerikanischen Raum wird bevorzugt die Lichtart D50 = 5000K gewählt (direkte Sonnenstrahlung), in Europa üblicherweise nach EN-Norm die Normlichtart D65 = 6500K (bedeckter Himmel bei Abmusterung am Nordfenster). Nachstehend die jeweiligen XnYnZn-Werte, welche in die Berechnungsformeln einzutragen sind.[4]
| Lichtart | Xn(2°) | Yn(2°) | Zn(2°) | Xn(10°) | Yn(10°) | Zn(10°) |
|---|---|---|---|---|---|---|
| D50 | 96,422 | 100 | 82,521 | 96,720 | 100 | 81,427 |
| D65 | 95,047 | 100 | 108,883 | 94,811 | 100 | 107,304 |
- Helligkeit
- Grün−Rot
- Gelb−Blau
Die Faktoren 500 bzw. 200 sollen die resultierenden Werte für a* und b* in die gewohnten Größenordnungen bringen, die auch zum maximalen L* von 100 passen.
- Für kleine Werte
wird die dritte Wurzel durch die folgende Beziehung ersetzt:
dabei steht P je für X, Y, Z.
Umrechnung von Lab zu HLC

Der LCh-Farbraum mit den Koordinaten (L*C*h°) entspricht dem Lab-Farbraum, in dem die kartesischen Koordinaten a* und b* als Polarkoordinaten C* (Abstand vom Ursprung) und h° (Winkel zur a-Achse) angegeben werden. Hierdurch werden CIELAB-Koordinate anschaulicher: h° kann als Basisfarbe (Hue) interpretiert werden und C* als deren Intensität (Chroma, Chromazität).
Für die polare Darstellung ist die Schreibweise HLC gebräuchlich, in der die übliche Reihenfolge bei der Farbauswahl (Farbton H – Helligkeit L – Sättigung C) zum Ausdruck kommen. Weitere alternative Kürzel sind LCh oder LCH.
Aus L*a*b* lassen sich Farbton h° und Buntheit C* wie folgt berechnen:
- Farbton (Hue)
- Helligkeit (Luminanz)
- Buntheit (Chroma)
Der in zahlreichen Computerprogrammen genutzte HSB/HSL-Raum unterscheidet sich grundsätzlich vom HLC-Raum. Zwar wird jener ebenfalls mit „Farbton, Sättigung, Helligkeit“ interpretiert, er ist aber durch Umrechnung der technisch begründeten RGB-Definition weniger wahrnehmungsgerecht.
Umrechnung von RGB zu Lab
Farbräume sind komplexe mathematische Körper und die Umrechnung ist entsprechend systembezogen. Der RGB-Farbraum ist immer gerätespezifisch und Lab ist wahrnehmungsorientiert. Zudem umfasst der L*a*b*-Farbraum einen größeren Farbumfang als jeder (technisch fassbare) RGB-Farbraum. So muss bei Lab-RGB-Berechnungen geklärt sein, wie die außerhalb des (RGB-)Zielfarbraums liegenden Farben in diesen projiziert werden (Gamut Mapping).
Eine Transformation des jeweils vorliegenden RGB-Farbraums in den L*a*b*-Farbraum wird über den CIE 1931-Farbraum (XYZ-Koordinaten) geführt, wodurch zunächst Geräteunabhängigkeit erreicht wird. Als Beispiel folgen die Umrechnungsformeln von sRGB zu XYZ.
Aus diesen ermittelten XYZ-Werten werden die Lab-Werte errechnet. R, G und B Werte sind im Wertebereich 0…1 zu verwenden.[5]
Farbbeispiele
Diese Tabelle zeigt die äußerst möglichen sRGB- und CMYK-Farben für 36 Hue-Werte in 10er-Schritten (Hue=10…360, siehe Farbkreis). Der verwendete Hex-RRGGBB-Farbcode wird angezeigt, wenn der Mauszeiger auf das Feld „Farbmuster“ geführt wird.
| sRGB | H | L | C | L* | a* | b* | R | G | B | CMYK-Vorschau | H | L | C | L* | a* | b* | C | M | Y | K |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 55 | 80 | 55 | 78,8 | 13,9 | 248 | 29 | 112 | 10 | 50 | 75 | 50 | 73,9 | 13,0 | 2 | 96 | 31 | 1 | ||
| 20 | 55 | 85 | 55 | 79,9 | 29,1 | 252 | 51 | 88 | 20 | 50 | 75 | 50 | 70,5 | 25,7 | 3 | 94 | 53 | 1 | ||
| 30 | 55 | 90 | 55 | 77,9 | 45,0 | 252 | 30 | 60 | 30 | 50 | 80 | 50 | 69,3 | 40,0 | 3 | 94 | 73 | 1 | ||
| 40 | 55 | 105 | 55 | 80,4 | 67,5 | 255 | 16 | 13 | 40 | 50 | 80 | 50 | 61,3 | 51,4 | 8 | 88 | 92 | 1 | ||
| 50 | 60 | 95 | 60 | 61,1 | 72,8 | 250 | 87 | 0 | 50 | 60 | 75 | 60 | 48,2 | 57,5 | 3 | 69 | 88 | 0 | ||
| 60 | 65 | 85 | 65 | 42,5 | 73,6 | 243 | 123 | 0 | 60 | 60 | 75 | 60 | 37,5 | 65,0 | 10 | 63 | 100 | 2 | ||
| 70 | 75 | 85 | 75 | 29,1 | 79,9 | 255 | 163 | 0 | 70 | 70 | 75 | 70 | 25,7 | 70,5 | 6 | 46 | 94 | 1 | ||
| 80 | 80 | 80 | 80 | 13,9 | 78,8 | 249 | 187 | 21 | 80 | 75 | 80 | 75 | 13,9 | 78,8 | 9 | 33 | 99 | 1 | ||
| 90 | 90 | 85 | 90 | 0,0 | 85,0 | 255 | 224 | 32 | 90 | 85 | 90 | 85 | 0,0 | 90,0 | 7 | 13 | 99 | 0 | ||
| 100 | 95 | 90 | 95 | −15,6 | 88,6 | 245 | 247 | 24 | 100 | 80 | 80 | 80 | −13,9 | 78,8 | 28 | 7 | 98 | 0 | ||
| 110 | 95 | 95 | 95 | −32,5 | 89,3 | 215 | 255 | 13 | 110 | 75 | 70 | 75 | −23,9 | 65,8 | 43 | 3 | 95 | 0 | ||
| 120 | 90 | 95 | 90 | −47,5 | 82,3 | 166 | 249 | 29 | 120 | 70 | 65 | 70 | −32,5 | 56,3 | 55 | 2 | 92 | 0 | ||
| 130 | 90 | 105 | 90 | −67,5 | 80,4 | 106 | 255 | 34 | 130 | 60 | 65 | 60 | −41,8 | 49,8 | 72 | 9 | 100 | 1 | ||
| 140 | 85 | 95 | 85 | −72,8 | 61,1 | 25 | 245 | 83 | 140 | 60 | 65 | 60 | −49,8 | 41,8 | 77 | 2 | 96 | 0 | ||
| 150 | 85 | 80 | 85 | −69,3 | 40,0 | 0 | 244 | 131 | 150 | 55 | 65 | 55 | −56,3 | 32,5 | 87 | 6 | 94 | 1 | ||
| 160 | 85 | 70 | 85 | −65,8 | 23,9 | 0 | 243 | 163 | 160 | 50 | 70 | 50 | −65,8 | 23,9 | 99 | 7 | 92 | 1 | ||
| 170 | 90 | 60 | 90 | −59,1 | 10,4 | 48 | 255 | 205 | 170 | 50 | 65 | 50 | −64,0 | 11,3 | 99 | 8 | 76 | 1 | ||
| 180 | 90 | 55 | 90 | −55,0 | 0,0 | 46 | 255 | 224 | 180 | 50 | 60 | 50 | −60,0 | 0,0 | 99 | 9 | 64 | 1 | ||
| 190 | 90 | 50 | 90 | −49,2 | −8,7 | 64 | 253 | 242 | 190 | 50 | 60 | 50 | −59,1 | −10,4 | 100 | 9 | 54 | 1 | ||
| 200 | 90 | 50 | 90 | −47,0 | −17,1 | 47 | 252 | 255 | 200 | 50 | 60 | 50 | −56,4 | −20,5 | 100 | 9 | 42 | 2 | ||
| 210 | 85 | 45 | 85 | −39,0 | −22,5 | 67 | 234 | 253 | 210 | 55 | 55 | 55 | −47,6 | −27,5 | 96 | 6 | 31 | 1 | ||
| 220 | 80 | 45 | 80 | −34,5 | −28,9 | 53 | 217 | 251 | 220 | 55 | 60 | 55 | −46,0 | −38,6 | 100 | 5 | 17 | 0 | ||
| 230 | 75 | 45 | 75 | −28,9 | −34,5 | 44 | 201 | 246 | 230 | 60 | 60 | 60 | −38,6 | −46,0 | 93 | 1 | 4 | 0 | ||
| 240 | 70 | 50 | 70 | −25,0 | −43,3 | 0 | 187 | 249 | 240 | 55 | 60 | 55 | −30,0 | −52,0 | 95 | 16 | 0 | 0 | ||
| 250 | 70 | 50 | 70 | −17,1 | −47,0 | 52 | 183 | 255 | 250 | 45 | 55 | 45 | −18,8 | −51,7 | 99 | 39 | 0 | 0 | ||
| 260 | 65 | 55 | 65 | −9,6 | −54,2 | 44 | 166 | 255 | 260 | 45 | 50 | 45 | −8,7 | −49,2 | 90 | 47 | 0 | 0 | ||
| 270 | 55 | 65 | 55 | 0,0 | −65,0 | 0 | 136 | 245 | 270 | 40 | 50 | 40 | 0,0 | −50,0 | 91 | 59 | 0 | 0 | ||
| 280 | 50 | 75 | 50 | 13,0 | −73,9 | 14 | 117 | 248 | 280 | 35 | 50 | 35 | 8,7 | −49,2 | 92 | 71 | 0 | 0 | ||
| 290 | 40 | 95 | 40 | 32,5 | −89,3 | 0 | 81 | 245 | 290 | 30 | 50 | 30 | 17,1 | −47,0 | 92 | 81 | 2 | 0 | ||
| 300 | 30 | 125 | 30 | 62,5 | −108,3 | 0 | 21 | 250 | 300 | 30 | 50 | 30 | 25,0 | −43,3 | 84 | 86 | 3 | 1 | ||
| 310 | 45 | 115 | 45 | 73,9 | −88,1 | 155 | 33 | 255 | 310 | 30 | 55 | 30 | 35,4 | −42,1 | 78 | 92 | 0 | 1 | ||
| 320 | 50 | 110 | 50 | 84,3 | −70,7 | 203 | 0 | 244 | 320 | 35 | 55 | 35 | 42,1 | −35,4 | 63 | 91 | 0 | 0 | ||
| 330 | 60 | 105 | 60 | 90,9 | −52,5 | 255 | 18 | 239 | 330 | 40 | 55 | 40 | 47,6 | −27,5 | 49 | 89 | 1 | 0 | ||
| 340 | 60 | 90 | 60 | 84,6 | −30,8 | 255 | 42 | 202 | 340 | 40 | 60 | 40 | 56,4 | −20,5 | 41 | 95 | 6 | 1 | ||
| 350 | 55 | 85 | 55 | 83,7 | −14,8 | 247 | 0 | 161 | 350 | 45 | 70 | 45 | 68,9 | −12,2 | 21 | 97 | 2 | 0 | ||
| 360 | 55 | 80 | 55 | 80,0 | 0,0 | 246 | 27 | 136 | 360 | 50 | 75 | 50 | 75,0 | 0,0 | 3 | 96 | 0 | 0 |
Literatur
- Manfred Richter: Einführung in die Farbmetrik. 1984 ISBN 3-11-008209-8.
Einzelnachweise
- ↑ Richard Sewall Hunter: Photoelectric Color-Difference
Meter. In: JOSA. 38. Jahrgang, Nr. 7,
Juli 1948, S. 661
(
 opticsinfobase.org).
(Proceedings of the Winter Meeting of the Optical Society of America)
opticsinfobase.org).
(Proceedings of the Winter Meeting of the Optical Society of America)
- ↑ Richard Sewall Hunter: Accuracy, Precision, and
Stability of New Photo-electric Color-Difference Meter. In: JOSA. 38. Jahrgang,
Nr. 12, Dezember 1948,
S. 1094
(
 opticsinfobase.org).
(Proceedings of the Thirty-Third Annual Meeting of the Optical Society of America).
opticsinfobase.org).
(Proceedings of the Thirty-Third Annual Meeting of the Optical Society of America).
- ↑ Hochspringen nach: a b c Der spektrale Hintergrund ist nur symbolisch und dekorativ und deckt sich nicht unmittelbar mit den Spektralfarben der zugehörigen Wellenlänge.
- ↑
 EasyRGB.
EasyRGB.
- ↑
 Welcome to Bruce Lindbloom's Web Site.
Welcome to Bruce Lindbloom's Web Site.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 05.04. 2024