Maxwell-Gleichungen

Die Maxwell-Gleichungen von James Clerk Maxwell (1831–1879) beschreiben die Phänomene des Elektromagnetismus. Sie sind damit ein wichtiger Teil des modernen physikalischen Weltbildes.

Die Gleichungen beschreiben, wie elektrische und magnetische Felder untereinander sowie mit elektrischen Ladungen und elektrischem Strom unter gegebenen Randbedingungen zusammenhängen. Zusammen mit der Lorentzkraft erklären sie alle Phänomene der klassischen Elektrodynamik. Sie bilden daher auch die theoretische Grundlage der Optik und der Elektrotechnik. Die Gleichungen sind nach dem schottischen Physiker James Clerk Maxwell benannt, der sie von 1861 bis 1864 erarbeitet hat. Er kombinierte dabei das Durchflutungsgesetz und das Gaußsche Gesetz mit dem Induktionsgesetz und führte zusätzlich, um die Kontinuitätsgleichung nicht zu verletzen, den ebenfalls nach ihm benannten Verschiebungsstrom ein.

James Clerk Maxwell

Die Maxwell-Gleichungen sind ein spezielles System von linearen partiellen Differentialgleichungen erster Ordnung. Sie lassen sich auch in integraler Form, in differentialgeometrischer Form und in kovarianter Form darstellen.

Maxwell-Gleichungen im Feldlinienbild

Die Feldlinien des elektrischen Feldes verlaufen zwischen den positiven und negativen Ladungen.

Die Feldlinien der magnetischen Flussdichte ${\vec {B}}$ bilden geschlossene Bahnen oder sind unendlich lang.

Das elektrische und das magnetische Feld können durch Feldlinien repräsentiert werden. Das elektrische Feld wird durch die Felder der elektrischen Feldstärke ${\vec {E}}$ und der elektrischen Flussdichte ${\vec {D}}$ repräsentiert, während das magnetische Feld durch die Felder der magnetischen Feldstärke ${\vec {H}}$ und der magnetischen Flussdichte ${\vec {B}}$ repräsentiert wird.

Die elektrische Feldstärke ${\vec {E}}$ und die magnetische Flussdichte ${\vec {B}}$ können prinzipiell durch die Kraftausübung auf Ladungen veranschaulicht werden. Die Zusammenhänge werden im Artikel über die Lorentzkraft genauer beschrieben. Im Falle des elektrischen Feldes zeigt der Verlauf der elektrischen Feldstärke die Richtung der vom Feld ausgeübten Kraft an (die Kraft wirkt in Richtung der Tangente an die Feldlinie am jeweiligen Ort), die Feldliniendichte (die Nähe der Feldlinien zueinander) stellt die Feldstärke in diesem Gebiet dar. Im Falle des magnetischen Feldes wirkt die Kraft normal zur Richtung der magnetischen Flussdichte und normal zur Bewegungsrichtung der Ladung.

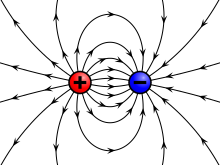
In der folgenden Abbildung wird das Feldlinienbild anhand einer positiven und einer negativen Ladung verdeutlicht. Das elektrische Feld ist an den Ladungsträgern am stärksten und nimmt mit größerer Entfernung ab:

In Quellenfeldern zeichnen sich die Feldlinien durch einen Anfang und ein Ende aus (oder verschwinden im Unendlichen). In Wirbelfeldern sind die Feldlinien geschlossene Kurven.

Das Gaußsche Gesetz für elektrische Felder besagt, dass elektrische Ladungen Quellen und Senken des Feldes der elektrischen Flussdichte ${\vec {D}}$ sind, also Anfang und Ende der zugehörigen Feldlinien darstellen. Elektrische Felder ohne Quellen und Senken, sogenannte Wirbelfelder, treten hingegen bei Induktionsvorgängen auf.
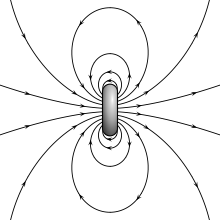
Das Gaußsche Gesetz für den Magnetismus besagt, dass das Feld der magnetischen Flussdichte ${\vec {B}}$ keine Quellen aufweist. Die magnetische Flussdichte hat demzufolge nur Feldlinien, welche kein Ende besitzen. Eine magnetische Feldlinie ist daher entweder unendlich lang oder führt in einer geschlossenen Bahn wieder auf sich selbst zurück.
Induktionsgesetz von Faraday: Zeitliche Änderungen des magnetischen Flusses führen zu einem elektrischen Wirbelfeld.
Erweitertes Ampèresches Gesetz, auch Durchflutungs- oder Maxwell-Ampèresches Gesetz genannt: Elektrische Ströme – einschließlich einer zeitlichen Änderung der elektrischen Flussdichte – führen zu einem magnetischen Wirbelfeld.

Gleichungen

Im engeren Sinne sind die Maxwell-Gleichungen die mathematische Beschreibung dieser Gesetze. Direkt analog zu den Gesetzen kann man sie mit vier gekoppelten Differentialgleichungen beschreiben, es gibt jedoch auch weitere äquivalente Formulierungen.

Notation

Es werden die Methoden der Vektoranalysis (und damit verbunden Oberflächenintegral, Kurvenintegral) verwendet. ${\vec {\nabla }}$ bezeichnet den Nabla-Operator. Die Differentialoperatoren bedeuten:

${\vec {\nabla }}\cdot {\vec {E}}\equiv \operatorname {div} {\vec {E}}$ bezeichnet die Divergenz von ${\vec {E}}$
${\vec {\nabla }}\times {\vec {E}}\equiv \operatorname {rot} {\vec {E}}$ bezeichnet die Rotation von ${\vec {E}}$

Mikroskopische Maxwell-Gleichungen

Die mikroskopischen Maxwell-Gleichungen verknüpfen die elektrische Feldstärke ${\vec {E}}$ und die magnetische Flussdichte ${\vec {B}}$ mit der Ladungsdichte $\,\rho$ (Ladung pro Volumen) und der elektrischen Stromdichte ${\vec {j}}$ (Strom pro durchflossene Fläche).

Name	SI	Physikalischer Inhalt
Gaußsches Gesetz	${\vec {\nabla }}\cdot {\vec {E}}={\frac {\rho }{\varepsilon _{0}}}$	Elektrische Feldlinien divergieren voneinander unter Anwesenheit elektrischer Ladung; die Ladung ist Quelle des elektrischen Feldes.
Gaußsches Gesetz für Magnetfelder	${\vec {\nabla }}\cdot {\vec {B}}=0$	Magnetische Feldlinien divergieren nicht, das Feld der magnetischen Flussdichte ist quellenfrei; es gibt keine magnetischen Monopole.
Induktionsgesetz	${\vec {\nabla }}\times {\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}}$	Änderungen der magnetischen Flussdichte führen zu einem elektrischen Wirbelfeld. Das Minuszeichen schlägt sich in der Lenzschen Regel nieder.
Erweitertes Durchflutungsgesetz	${\vec {\nabla }}\times {\vec {B}}=\mu _{0}{\vec {j}}+\mu _{0}\varepsilon _{0}{\frac {\partial {\vec {E}}}{\partial t}}$	Elektrische Ströme – einschließlich des Verschiebungsstroms – führen zu einem magnetischen Wirbelfeld.

Dabei kann auch $\mu _{0}\varepsilon _{0}={\frac {1}{c^{2}}}$ eingesetzt werden.

Makroskopische Maxwell-Gleichungen

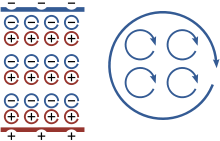
>Mikroskopische elektrische Dipole und Kreisströme sowie die nicht dargestellten Spindipole (relativistische Quantentheorie) führen zu makroskopischen Polarisationen ${\vec {P}}$ bzw. ${\vec {M}}$ .

Bei Anwesenheit von Materie sind die mikroskopischen Maxwell-Gleichungen einerseits unhandlich, da schließlich jeder Ladungsträger in jedem Atom des Mediums berücksichtigt werden muss. Andererseits können die magnetischen Eigenschaften (beispielsweise von einem Permanentmagneten) prinzipiell nicht ohne zusätzliche physikalische Erkenntnisse der Quantenmechanik aus den mikroskopischen Maxwell-Gleichungen abgeleitet werden.

Die makroskopischen Maxwell-Gleichungen berücksichtigen die Eigenschaften der Materie in Form von Materialparametern, wobei dem leeren Raum die Parameter Permittivität $\varepsilon _{0}$ und Permeabilität $\mu _{0}$ zugeordnet werden. Maxwell selbst ging nicht von einem leeren Raum, sondern – wie zu seiner Zeit üblich – von dem mit einem sogenannten „Äther“ erfüllten Raum aus. Die Bezeichnung „makroskopisch“ kommt dadurch zustande, dass die Eigenschaften der Materie letztlich örtlich gemittelte Eigenschaften der Materie kennzeichnen. Im Hinblick auf die Ladungen wird dabei zwischen freien Ladungsträgern (etwa Leitungselektronen im elektrischen Leiter) und gebundenen Ladungsträgern (etwa Hüllenelektronen) unterschieden, und es wird davon ausgegangen, dass die gebundenen Ladungsträger durch mikroskopische Prozesse^[1] zu einer makroskopischen Polarisation ${\vec {P}}$ bzw. Magnetisierung ${\vec {M}}$ führen.

Die Anwesenheit von Materie erfordert, dass das elektrische und das magnetische Feld jeweils durch zwei zusätzliche Vektorfelder beschrieben werden, die elektrische Flussdichte ${\vec {D}}:={\varepsilon _{0}}{\vec {E}}+{\vec {P}}$ und die magnetische Feldstärke ${\vec {H}}:={\frac {1}{\mu _{0}}}{\vec {B}}-{\vec {M}}$ .

Name	SI	Physikalischer Inhalt
Gaußsches Gesetz	${\vec {\nabla }}\cdot {\vec {D}}=\rho _{\text{frei}}$	Die Ladung ist Quelle des elektrischen Feldes.
Gaußsches Gesetz für Magnetfelder	${\vec {\nabla }}\cdot {\vec {B}}=0$	Das Feld der magnetischen Flussdichte ist quellenfrei; es gibt keine magnetischen Monopole.
Induktionsgesetz	${\vec {\nabla }}\times {\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}}$	Änderungen des magnetischen Feldes führen zu einem elektrischen Wirbelfeld.
Erweitertes Durchflutungsgesetz	${\vec {\nabla }}\times {\vec {H}}={\vec {j}}_{\text{frei}}+{\frac {\partial {\vec {D}}}{\partial t}}$	Elektrische Ströme – einschließlich des Verschiebungsstroms – führen zu einem magnetischen Wirbelfeld.

und es ist z.B. $\rho _{\mathrm {frei} }=\rho -\rho _{\mathrm {pol} }=\rho +\operatorname {div} {\vec {P}}\,.$

Differentielle und integrale Formulierung

In den folgenden Abschnitten bzw. Tabellen wird bezüglich der Indizierung von Ladung und Strom eine semantisch äquivalente Konvention benutzt: Und zwar werden $\rho _{\mathrm {frei} }$ bzw. ${\vec {j}}_{\mathrm {frei} }$ ohne Index geschrieben und als „wahre Ladungen“ bzw. „wahre Ströme“ bezeichnet, während umgekehrt die in den 'mikroskopischen Gleichungen' auftretenden nicht-indizierten Größen als Effektivgrößen $\rho _{E}$ bzw. ${\vec {j}}_{B}$ geschrieben werden. Im Vakuum gelten die „mikroskopischen Gleichungen“ und auf die Indizierung kann verzichtet werden. Die folgenden Gleichungen gelten dagegen in Materie, und man ist auf eine einheitliche Schreibweise angewiesen, meistens die unten benutzte, obwohl auch hier unterschiedliche Konventionen nicht ausgeschlossen sind.

Übersicht

Hier werden u.a. die Maxwell-Gleichungen in SI-Einheiten angegeben. Formulierungen in anderen Einheitensystemen sind am Schluss aufgeführt bzw. werden durch Bemerkungen im Text erläutert.

Die im Folgenden in der rechten Spalte im Zentrum von einfachen oder zweifachen Integralen angegebenen Symbole betonen, dass man es mit geschlossenen Kurven bzw. Flächen zu tun hat.

**Maxwell-Gleichungen in SI-Einheiten**
differentielle Form
Physikalisches gaußsches Gesetz: Das ${\vec {D}}$ -Feld ist ein Quellenfeld. Die Ladung (Ladungsdichte $\rho$ ) ist Quelle des elektrischen Feldes.	Gauß	Der (elektrische) Fluss durch die geschlossene Oberfläche $\partial V$ eines Volumens ist direkt proportional zu der elektrischen Ladung in seinem Inneren.
$\operatorname {div} {\vec {D}}={\vec {\nabla }}\cdot {\vec {D}}=\rho$	$\Longleftrightarrow$	$\iint _{\partial V}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\subset \!\supset {\vec {D}}\cdot \mathrm {d} {\vec {A}}=\iiint _{V}\rho \ \mathrm {d} V=Q(V)$
Quellenfreiheit des B-Feldes: Das ${\vec {B}}$ -Feld ist quellenfrei. Es gibt keine magnetischen Monopole.	Gauß	Der magnetische Fluss durch die geschlossene Oberfläche eines Volumens ist gleich der magnetischen Ladung in seinem Inneren, nämlich Null, da es keine magnetischen Monopole gibt.
$\operatorname {div} {\vec {B}}={\vec {\nabla }}\cdot {\vec {B}}=0$	$\Longleftrightarrow$	$\iint _{\partial V}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\subset \!\supset {\vec {B}}\cdot \mathrm {d} {\vec {A}}=0$
Induktionsgesetz: Jede Änderung des ${\vec {B}}$ -Feldes führt zu einem elektrischen Gegenfeld. Die Wirbel des elektrischen Feldes sind von der zeitlichen Änderung der magnetischen Flussdichte abhängig.	Stokes	Die (elektrische) Zirkulation über der Randkurve $\partial A$ einer Fläche ist gleich der negativen zeitlichen Änderung des magnetischen Flusses durch die Fläche.^[2]
$\operatorname {rot} {\vec {E}}={\vec {\nabla }}\times {\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}}$	$\Longleftrightarrow$	$\oint _{\!\partial A}\!\!\!{\vec {E}}\cdot \mathrm {d} {\vec {s}}=-\!\!\iint _{A}\!{\frac {\partial {\vec {B}}}{\partial t}}\cdot \mathrm {d} {\vec {A}}$
Durchflutungsgesetz: Die Wirbel des Magnetfeldes hängen von der Leitungsstromdichte $\textstyle {\vec {j}}_{\mathrm {l} }$ und von der elektrischen Flussdichte $\textstyle {\vec {D}}$ ab. Die zeitliche Änderung von ${\vec {D}}$ wird auch als Verschiebungsstromdichte ${\vec {j}}_{\mathrm {v} }$ bezeichnet und ergibt als Summe mit der Leitungsstromdichte die totale Stromdichte ${\vec {j}}_{\,{\text{total}}}={\vec {j}}_{\mathrm {l} }+{\vec {j}}_{\mathrm {v} }$ ^[3]	Stokes	Die magnetische Zirkulation über der Randkurve $\partial A$ einer Fläche ist gleich der Summe aus dem Leitungsstrom und der zeitlichen Änderung des elektrischen Flusses durch die Fläche.^[2]
$\operatorname {rot} {\vec {H}}={\vec {\nabla }}\times {\vec {H}}={\vec {j}}_{\mathrm {l} }\;+\;{\frac {\partial {\vec {D}}}{\partial t}}$	$\Longleftrightarrow$	$\oint _{\!\partial A}\!\!\!{\vec {H}}\cdot \mathrm {d} {\vec {s}}=\iint _{A}\!{\vec {j}}_{\mathrm {l} }\cdot \mathrm {d} {\vec {A}}\;\;+\;\;\iint _{A}\!{\frac {\partial {\vec {D}}}{\partial t}}\cdot \mathrm {d} {\vec {A}}$

Erläuterungen

Zu beachten ist, dass alle Größen aus einem beliebigen, aber für alle Größen gleichen Inertialsystem gemessen werden müssen. Soll mithilfe der o.g. Gleichungen beispielsweise die induzierte Spannung in einer bewegten Leiterschleife betrachtet werden, so ist es günstig, die Größen in den bewegten Teilen des Systems mithilfe der Lorentztransformation in das Ruhesystem umzurechnen.

In diesem Zusammenhang sei erwähnt, dass manche Lehrbücher anstelle des Induktionsgesetzes folgende Näherung notieren:

$\oint _{\partial A}{\vec {E}}'\cdot {\text{d}}{\vec {s}}=-\iint _{A}{\frac {\partial {\vec {B}}}{\partial t}}\cdot {\text{d}}{\vec {A}}+\oint _{\partial A}{\vec {v}}\times {\vec {B}}\cdot {\text{d}}{\vec {s}}\,\,\left(=-{\frac {\text{d}}{{\text{d}}t}}\iint _{A}{\vec {B}}\cdot {\text{d}}{\vec {A}}\,\right),$

wobei die Feldstärke $\vec E'$ jeweils in einem Bezugssystem gemessen wird, in dem das Linienelement ${\mathrm {d}}{\vec s}$ ruht. Diese Gleichung gilt nur für Geschwindigkeiten, die klein sind im Vergleich zur Lichtgeschwindigkeit, $|{\vec {v}}|\ll c.$

Elektrischer Strom

In der elektrischen Stromdichte ${\vec {j}}$ kann rein formal sowohl die übliche Leitungsstromdichte entsprechend dem Fluss von elektrischen Ladungsträgern als auch die Verschiebungsstromdichte (die zeitliche Änderung der elektrischen Flussdichte) zusammengefasst werden, was eine wichtige Rolle bei der Entdeckung der Maxwell-Gleichungen durch Maxwell spielte. Üblicherweise wird aber der Verschiebungsstrom getrennt aufgeführt. Die elektrische Stromdichte ist über die Materialgleichungen der Elektrodynamik und die dabei auftretende elektrische Leitfähigkeit $\sigma$ mit der elektrischen Feldstärke ${\vec {E}}$ verknüpft.

Elektrisches Feld

${\vec {D}}$ ist die elektrische Flussdichte, historisch und etwas verwirrend auch als elektrische Verschiebungsdichte oder als elektrische Erregung bezeichnet. Dabei handelt es sich um die Dichte des elektrischen Flusses, welcher von elektrischen Ladungen ausgeht. Die elektrische Flussdichte ist über die Materialgleichungen der Elektrodynamik und die dabei auftretende dielektrische Leitfähigkeit $\varepsilon$ mit der elektrischen Feldstärke ${\vec {E}}$ verknüpft. Noch allgemeiner gilt ${\vec {D}}=\varepsilon _{0}\,{\vec {E}}+{\vec {P}}$ mit der elektrischen Polarisation ${\vec {P}}$ , dem elektrischen Dipolmoment pro Volumen.

Magnetisches Feld

${\vec {B}}$ ist die magnetische Flussdichte, auch historisch als Induktion bezeichnet. Dabei handelt es sich um die Dichte des magnetischen Flusses, welcher von bewegten elektrischen Ladungen oder von Permanentmagneten verursacht wird. Die magnetische Flussdichte ist über die Materialgleichungen der Elektrodynamik und die dabei auftretende magnetische Leitfähigkeit $\mu$ mit der magnetischen Feldstärke ${\vec {H}}$ verknüpft. Noch allgemeiner gilt ${\vec {B}}=\mu _{0}{\vec {H}}+{\vec {J}}$ mit der magnetischen Polarisation ${\vec {J}}$ , dem magnetischen Dipolmoment pro Volumen (als Magnetisierung wird die im Weiteren zu ${\vec {J}}$ äquivalente Größe ${\vec {M}}={\frac {\vec {J}}{\mu _{0}}}$ bezeichnet).

Die magnetische Polarisation ${\vec {J}}$ sollte nicht mit der Stromdichte ${\vec {j}}$ (genauer: mit der Leitungsstromdichte) verwechselt werden. Vielmehr gilt:

$\operatorname {rot} {\frac {{\vec {B}}-{\vec {J}}}{\mu _{0}}}={\vec {j}}+{\frac {\partial {\vec {D}}}{\partial t}}$

Erläuterung zu den Maxwell-Gleichungen mit Materie

Die in allen drei Bereichen auftretenden Materialgleichungen werden nicht direkt zu den Maxwell-Gleichungen gezählt, sondern die drei Gleichungssätze:

Maxwell-Gleichungen
Materialgleichungen der Elektrodynamik
Kontinuitätsgleichungen der Elektrodynamik

stellen gemeinsam und unter gegenseitiger Ergänzung das Fundament der elektrodynamischen Feldtheorie dar. Die Materialgleichungen gelten in der allgemeinen Form sowohl für den leeren Raum als auch für mit Materie ausgefüllte Raumbereiche.

Aus historischen Gründen, und manchmal auch um bestimmte Berechnungsvorgänge spezifisch darzustellen, werden die Materialgleichungen und die darin auftretenden drei Leitfähigkeiten jeweils in den Anteil des leeren Raumes $\varepsilon _{0}$ bzw. $\mu _{0}$ und den Anteil der Leitfähigkeit, welcher durch die Materie verursacht wird, $\varepsilon _{\mathrm {r} }$ und $\mu _{\mathrm {r} }$ aufgespalten.

Für das elektrische Feld ergibt sich durch die Aufspaltung der dielektrischen Leitfähigkeit die Möglichkeit zur Einführung eines weiteren Vektorfeldes, der elektrischen Polarisation ${\vec {P}}$ (eigentlich dielektrische Polarisation, die aber auch als elektrische Polarisation bezeichnet wird, da dem elektrischen Feld zugewiesen).

Analog dazu beschreibt die magnetische Polarisation ${\vec {J}}$ die von den Eigenschaften des leeren Raumes losgelösten Verhältnisse in Materie für das magnetische Feld. Aus der magnetischen Polarisation ergibt sich die Magnetisierung ${\vec {M}}={\tfrac {\vec {J}}{\mu _{0}}}$ . (Im cgs-System sind die Verhältnisse verwirrender: ${\vec {J}}$ und ${\vec {M}}$ werden dort gleich bezeichnet, als cgs-Magnetisierung, und unterscheiden sich nur um einen Faktor $4\pi$ , je nachdem ob ${\vec {B}}$ oder ${\vec {H}}$ gemeint ist.)

Grundsätzlich kann ohne Verlust auf die Einführung der Vektorfelder der elektrischen Polarisation ${\vec {P}}$ und der magnetischen Polarisation ${\vec {J}}$ (bzw. der dazu äquivalenten Magnetisierung ${\vec {M}}$ ) verzichtet werden. Stattdessen werden die Abhängigkeiten in den Materialgleichungen und den entsprechend allgemein gefassten Leitfähigkeiten in Form von Tensoren höherer Ordnung berücksichtigt. Weiterhin können die Leitfähigkeiten auch Funktionen darstellen, um nichtlineare Eigenschaften der Materie erfassen zu können. Diese können sogar von der Vorbehandlung abhängen, also explizit zeitabhängig sein. Diese Vorgangsweise empfiehlt sich auch für einen systematischen Zugang, wenn dieser über das SI-Einheitensystem erfolgt. Aus historischen Gründen, aber auch in bestimmten Teilbereichen der Physik, wird allerdings manchmal sehr intensiv von den ${\vec {P}}$ - und ${\vec {J}}$ - (bzw. ${\vec {M}}$ -)Vektorfeldern Gebrauch gemacht, weshalb im Folgenden dieser Sachverhalt näher dargestellt wird.

In Materie gilt allgemein

${\vec {D}}=\varepsilon _{0}{\vec {E}}+{\vec {P}}$

sowie

${\vec {H}}={\frac {1}{\mu _{0}}}{\vec {B}}-{\vec {M}}$

bzw.

${\vec {B}}=\mu _{0}({\vec {H}}+{\vec {M}})=\mu _{0}{\vec {H}}+{\vec {J}}\,,$ mit der oben eingeführten „magnetischen Polarisation“ ${\vec {J}}=\mu _{0}{\vec {M}}$ ,

wobei sich im Spezialfall der Linearität bei Isotropie oder bei kubischen Systemen noch folgende Vereinfachung ergibt:

${\vec {D}}=\varepsilon _{0}\varepsilon _{\mathrm {r} }\,{\vec {E}}$

und

${\vec {B}}=\mu _{0}\mu _{\mathrm {r} }\,{\vec {H}}$ .

In homogenen isotropen Materialien (d.h. die Größen $\varepsilon \,\,(=\varepsilon _{0}\varepsilon _{\mathrm {r} })\,$ und $\mu \,\,(=\mu _{0}\mu _{\mathrm {r} })$ sind skalar und konstant) erhält man für die Maxwell-Gleichungen

${\vec {\nabla }}\times {\vec {H}}=\varepsilon \,{\frac {\partial {\vec {E}}}{\partial t}}+\sigma \,{\vec {E}}$

$-{\vec {\nabla }}\times {\vec {E}}=\mu \,{\frac {\partial {\vec {H}}}{\partial t}}$

$\varepsilon \,{\vec {\nabla }}\cdot {\vec {E}}=\rho$

$\mu \,{\vec {\nabla }}\cdot {\vec {H}}=0$ .

In anisotroper nicht-kubischer linearer Materie werden die Skalare $\varepsilon _{\mathrm {r} }$ und $\mu _{\mathrm {r} }$ zu Tensoren 2. Stufe, wobei die Beziehungen weiterhin Gültigkeit behalten. In nichtlinearen Materialien hängen die Leitfähigkeiten von den jeweiligen Momentanwerten der Feldstärken oder im allgemeinsten Fall von deren gesamter Geschichte ab (siehe Hysterese). Die ${\vec {P}}$ - und ${\vec {J}}$ -Felder, elektrische bzw. magnetische Polarisation genannt, verschwinden außerhalb der Materie, was in den genannten Spezialfällen gleichwertig mit der Aussage ist, dass $\varepsilon _{\mathrm {r} }=\mu _{\mathrm {r} }=1$ wird.

Die dielektrische Polarisation ist dann mit der elektrischen Suszeptibilität $\chi _{e}$ , bzw. der relativen Permittivität $\varepsilon _{r}$ > und der Vakuum-Permittivität (Dielektrizitätskonstante) $\varepsilon _{0}$ folgendermaßen verknüpft (im SI, d.h. in der Einheit $\mathrm {\tfrac {A\,s}{V\,m}}$ ):

${\vec {P}}=\varepsilon _{0}\chi _{e}{\vec {E}}=\varepsilon _{0}\cdot ({\varepsilon _{\mathrm {r} }}-1){\vec {E}}$ ,

mit

$\varepsilon _{\mathrm {r} }=1+\chi _{e}$ .

Für die magnetische Polarisation ${\vec {J}}$ bzw. die Magnetisierung ${\vec {M}}={\tfrac {\vec {J}}{\mu _{0}}}$ gilt eine entsprechende Gleichung mit der magnetischen Suszeptibilität $\chi _{m}$ bzw. der relativen Permeabilität $\mu _{\mathrm {r} }$ und der Vakuum-Permeabilität (magnetische Feldkonstante) $\mu _{0}$ mit der Einheit $\mathrm {\tfrac {V\,s}{A\,m}}$ :

${\vec {J}}=\mu _{0}\,\chi _{m}\,{\vec {H}}=\mu _{0}\cdot \left(\mu _{\mathrm {r} }-1\right)\,{\vec {H}}$ ,

mit

$\mu _{\mathrm {r} }=1+\chi _{m}$ .

(Vorsicht: im cgs-System sind $\chi _{e}$ und $\chi _{m}$ mit $4\pi$ zu multiplizieren!)

Weiter ergibt sich die Definition des Brechungsindex mit

$n:={\sqrt {\varepsilon _{\mathrm {r} }\,\mu _{\mathrm {r} }}}$

und der Zusammenhang zwischen Lichtgeschwindigkeit und elektrischer und magnetischer Feldkonstante

$c={\frac {1}{\sqrt {\varepsilon _{0}\,\mu _{0}}}}$ .

Dies bringt die Ausbreitung von Licht in Materie mit den Konstanten des Mediums in Verbindung. So ist die Phasengeschwindigkeit im Medium

$c_{p}={\frac {c}{n}}={\frac {1}{\sqrt {\varepsilon _{0}\,\mu _{0}\,\varepsilon _{\mathrm {r} }\,\mu _{\mathrm {r} }}}}$ ,

die ohne Dispersion gleich der Gruppengeschwindigkeit ist.

Zusammenfassung

Maxwell-Gleichungen in Materie in SI-Einheiten
Durchflutungsgesetz	${\vec {\nabla }}\times {\vec {H}}={\frac {\partial {\vec {D}}}{\partial t}}+{\vec {j}}$
Induktionsgesetz	${\vec {\nabla }}\times {\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}}$
Gaußsches Gesetz	${\vec {\nabla }}\cdot {\vec {D}}=\rho$
Gaußsches Gesetz des Magnetismus	${\vec {\nabla }}\cdot {\vec {B}}=0$
siehe Erläuterung	${\vec {D}}=\varepsilon _{0}\,{\vec {E}}+{\vec {P}}\quad$ (oder auch ${\vec {D}}=\varepsilon \,{\vec {E}}$ )
siehe Erläuterung	${\vec {B}}=\mu _{0}\,({\vec {H}}+{\vec {M}})\quad$ (oder auch ${\vec {B}}=\mu \,{\vec {H}}$ )

Erläuterung:
Die zuletzt angegebenen, eingeklammerten Beziehungen gelten nur bei linearem Zusammenhang. Die davor angegebenen Definitionen von ${\vec {P}}$ und ${\vec {M}}$ sind dagegen allgemein.

Traditionell werden die beiden zuletzt angegebenen sogenannten Materialgesetze und das ohmsche Gesetz ${\vec {j}}=\sigma \,{\vec {E}}$ ( $\sigma$ ist hier der spezifische elektrische Leitwert) meist nicht in die Maxwell-Gleichungen miteinbezogen. Die Kontinuitätsgleichung ${\tfrac {\partial \rho }{\partial t}}+\operatorname {div} \,{\vec {j}}=0\,$ als Beschreibung der Ladungserhaltung folgt aus den Maxwell-Gleichungen.

Die elektrischen Feldstärken ${\vec {E}}$ sowie die magnetischen Flussdichten ${\vec {B}}$ werden als physikalisch vorhandene Kraftfelder interpretiert. Schon Maxwell verband diese Kraftfelder mit dem elektrischen Potenzialfeld $\,\phi$ und dem Vektorpotential ${\vec {A}}$ :

${\vec {E}}=-{\vec {\nabla }}\,\phi -{\frac {\partial {\vec {A}}}{\partial t}}\,,$

${\vec {B}}={\vec {\nabla }}\times {\vec {A}}\,.$

Der Zusammenhang zwischen Feldstärken und Potentialen ist zwar nur bis auf Eichtransformationen definiert, den Potentialen kommt aber in der Quantentheorie eine fundamentale Bedeutung zu.

Maxwell-Gleichungen mit Differentialformen (differentialgeometrische Formulierung)

Die Beschreibung durch die Vektoranalysis hat den großen Nachteil, dass sie

auf den flachen $\mathbb {R} ^{3}$ bzw. $\mathbb {R} ^{4}$ beschränkt ist
prinzipiell „metrisch verseucht“ ist, da entweder die euklidische oder die Minkowski-Metrik in den Operatoren verbaut ist, obwohl die Maxwell-Gleichungen metrikfrei definiert sind
die Wahl einer Karte der zugrunde liegenden Mannigfaltigkeit unphysikalisch ist, da Naturgesetze unabhängig von den gewählten Koordinaten richtig sein müssen.

Es ist deshalb besser, die Gleichungen mit alternierenden Differentialformen zu schreiben und somit konsequent die Methoden der Differentialgeometrie zu benutzen.

Der dreidimensionale Ansatz

In diesem dreidimensionalen Ansatz wird die Zeit als äußerer Parameter behandelt, wie aus der klassischen Mechanik gewohnt.

Die inhomogenen Maxwell-Gleichungen

Sei $\rho \in \Lambda ^{3}({\mathcal {M}})$ eine Differentialform auf der beliebigen glatten Mannigfaltigkeit ${\mathcal {M}}$ der Dimension 3 und $\mathrm {d}$ die Cartan’sche äußere Ableitung. Dann gilt also

$\mathrm {d} \rho =0\quad \Leftrightarrow \quad \rho {\text{ ist eine geschlossene Differentialform}}\,,$

weil es keine von 0 verschiedene Differentialform vom Grad 4 auf einer dreidimensionalen Mannigfaltigkeit geben kann. Auf einem sternförmigen Gebiet sichert das Lemma von Poincaré, dass eine Potentialform $D\in \Lambda ^{2}({\mathcal {M}})$ existiert, so dass

$\mathrm {d} D=\rho \quad \Leftrightarrow \quad \int _{\mathcal {M}}\mathrm {d} D=\int _{\mathcal {M}}\rho \quad {\stackrel {\text{Stokes}}{\Longleftrightarrow }}\quad \oint _{\partial {\mathcal {M}}}D=\int _{\mathcal {M}}\,\,\rho \quad$ (Gesetz von Gauß).

Weiterhin wird postuliert, dass die zeitliche Ableitung der Ladung $\partial _{t}Q$ aus einer Mannigfaltigkeit einem Strom durch die Berandung entgegengesetzt ist (sprich: Alles was aus dem „Volumen“ ${\mathcal {M}}$ herauswill, muss durch die Berandungsfläche $\partial {\mathcal {M}}$ fließen).

$\partial _{t}Q=-I\quad \Leftrightarrow \quad \partial _{t}\int _{\mathcal {M}}\rho +\oint _{\!\partial {\mathcal {M}}}j=0\quad {\stackrel {\text{Stokes}}{\Longleftrightarrow }}\quad \int _{\mathcal {M}}\underbrace {\left(\partial _{t}\rho +\mathrm {d} j\right)} _{\text{Kontinuitätsgleichung}}=0\,.$

Diese Aussage entspricht also dem zur Kontinuitätsgleichung gehörigen Erhaltungssatz für die Gesamtladung (die Beliebigkeit der Mannigfaltigkeit ${\mathcal {M}}$ sichert analog zum Gesetz von Gauß, dass dieser auch ohne Integrale gilt). $j\in \Lambda ^{2}({\mathcal {M}})$ wird Stromdichte(zweiform) genannt. Also:

$\partial _{t}\rho +\mathrm {d} j=0\quad \Leftrightarrow \quad \mathrm {d} (\partial _{t}D+j)=0\quad \Leftrightarrow \quad (\partial _{t}D+j){\text{ ist eine geschlossene Differentialform}}\,.$

Diese mathematische Aussage impliziert aber nach dem Lemma von Poincaré, dass auf einem sternförmigen Gebiet eine Differentialform vom Grad 1 $H\in \Lambda ^{1}({\mathcal {M}})$ existiert, sodass

$\mathrm {d} H=\partial _{t}D+j\quad \Leftrightarrow \quad \int _{\mathcal {S}}\mathrm {d} H=\int _{\mathcal {S}}\left(\partial _{t}D+j\right)\quad {\stackrel {\text{Stokes}}{\Longleftrightarrow }}\quad \oint _{\partial {\mathcal {S}}}H=\int _{\mathcal {S}}\left(\partial _{t}D+j\right)\quad$ (Maxwell-Ampère-Gesetz).

Anzumerken ist, dass das Gesetz von Gauß rein aus der Geometrie des Problems folgt, also letztlich keine physikalische Bedeutung hat: Der einzige physikalische Input ist die Existenz elektrischer Ladungen bzw. die Kontinuitätsgleichung, welche im Maxwell-Ampère-Gesetz mündet. Die inhomogenen Gleichungen sind also Folge der Ladungserhaltung. Nicht betroffen ist im Grunde nur der sogenannte Spinmagnetismus, d.h. derjenigen magnetischen Phänomene, die nicht von den hier ausschließlich behandelten Ampèreschen Kreisströmen (den Wirbeln von j ) herrühren (siehe Mathematische Struktur der Quantenmechanik, speziell den Abschnitt über den Spin, sowie den Artikel über das sogenannte gyromagnetische Verhältnis). Das betrifft den dominierenden Teil des Permanent-Magnetismus. Das zeigt aber im Grunde nur, dass die klassische Elektrodynamik nicht in sich selbst abgeschlossen ist, obwohl es mathematisch und theoretisch-physikalisch so scheint.

Die homogenen Maxwell-Gleichungen

Ähnlich der Kontinuitätsgleichung wird das Induktionsgesetz postuliert. Die zeitliche Änderung des magnetischen Flusses durch eine Fläche ${\mathcal {S}}$ geht einher mit der Induktion einer entgegengesetzten Ringspannung auf ihrem Rand $\partial S$ . Das ist völlig analog zur Kontinuitätsgleichung, nur eine Dimension tiefer.

$U=-\partial _{t}\Phi _{\text{mag}}\quad \Rightarrow \quad \oint _{\!\partial {\mathcal {S}}}E=-\int _{\mathcal {S}}\partial _{t}B\quad {\stackrel {\text{Stokes}}{\Longleftrightarrow }}\quad \int _{\mathcal {S}}\left(\mathrm {d} E+\partial _{t}B\right)=0\quad {\text{(Induktionsgesetz)}}$

Dabei ist $B\in \Lambda ^{2}({\mathcal {M}})$ die magnetische Flussdichte(zweiform) und $E\in \Lambda ^{1}({\mathcal {M}})$ das elektrische Feld. Die Beliebigkeit der Fläche ${\mathcal {S}}$ sichert, dass sich das Induktionsgesetz auch ohne Integral schreiben lässt:

$\mathrm {d} E+\partial _{t}B=0\quad {\stackrel {\mathrm {d} }{\Rightarrow }}\quad \underbrace {d^{2}} _{=0}E+\partial _{t}\mathrm {d} B=0\quad \Rightarrow \mathrm {d} B=f(x,y,z)$

Man erkennt also, dass $\mathrm {d} B$ nur von den (Raum)-Komponenten der Mannigfaltigkeit ${\mathcal {M}}$ abhängen kann, nicht aber von der Zeit. Jedoch hängt der Ausdruck links vom Gleichheitszeichen gar nicht von der Wahl der Koordinaten ab. Also muss f(x,y,z) verschwinden. Zusätzlich kann die Gleichung auch nur dann lorentzinvariant sein. Es folgt also die Quellfreiheit der magnetischen Flussdichte(zweiform) (d.h. die Nichtexistenz magnetischer Ladungen, siehe oben):

$\mathrm {d} B=0\quad \Leftrightarrow \quad \int _{\mathcal {M}}\mathrm {d} B=0\quad {\stackrel {\text{Stokes}}{\Longleftrightarrow }}\quad \oint _{\!\partial {\mathcal {M}}}B=0\quad {\text{(Quellfreiheit)}}$

Wieder geht lediglich ein Postulat ein, das Induktionsgesetz; die Quellfreiheit ist dann eine rein mathematische Konsequenz.

Die Materialgleichungen

Weil die Einsformen und nicht kompatibel mit den Zweiformen und sind, muss man eine Beziehung zwischen ihnen herstellen. Das geschieht mit dem Hodge-Stern-Operator , welcher auf einer dreidimensionalen Mannigfaltigkeit ein Isomorphismus zwischen Einsformen und Zweiformen ist.

$D=\varepsilon _{0}*E\quad {\text{und}}\quad B=\mu _{0}*H\quad {\text{(Materialgleichungen)}}$

Hier wird offensichtlich, warum und bzw. und schon aus mathematischen Gründen nicht einfach (bis auf einen Faktor) identifiziert werden können. ist ja eine Einsform und wird über eine Kurve integriert, ist eine Zweiform und braucht eine (2-dimensionale) Fläche zur Integration. (Zudem sind in polarisierbaren Medien die zugehörigen Vektorfelder auch physikalisch wesentlich verschieden.) Es kann also schon von der Mathematik her keine Proportionalität zwischen diesen Größen bestehen, wie es die Beschreibung durch die Vektoranalysis suggeriert. Gleiches gilt für und : Die erste Größe beschreibt eine Differentialform vom Grade 1, braucht zur Integration also eine Kurve, wie bei einem Kraft-Integral; die zweite Größe ist eine Zweiform, braucht also eine Fläche wie bei einem Fluss-Integral. Dieser Unterschied scheint pedantisch, ist aber fundamental.

Es sei bemerkt, dass erst mit dem Hodge-Operator die Metrik eine Rolle in den Gleichungen spielt. Die Maxwell-Gleichungen ohne die Materialgleichungen sind unabhängig von der Wahl der Metrik und sogar unabhängig von der Beschaffenheit der Mannigfaltigkeit, solange ${\mathcal {M}}$ dreidimensional ist. Lediglich die Wirkung von in den Materialgleichungen würde sich verändern.

Der vierdimensionale Ansatz

${\mathcal {N}}$ sei eine glatte Mannigfaltigkeit der Dimension 4 und ${\mathcal {M}}\subset {\mathcal {N}}$ eine glatte Untermannigfaltigkeit der Dimension 3 (aus dem 3-dimensionalen Ansatz) und $g\in {\mathcal {T}}_{2}^{0}({\mathcal {N}})$ der metrische Tensor mit Koeffizientendarstellung.

$g_{\mu \nu }=\left(\operatorname {diag} (-1,1,1,1)\right)_{\mu \nu }\quad {\text{(Minkowski-Metrik)}}$

(Es gibt viele äquivalente Formen, die man z.B. durch Multiplikation mit einer Zahl vom Betrag 1 erhalten kann.)

Die Metrik muss lediglich festgelegt werden, damit man das nun folgende Viererpotential $A\in \Lambda ^{1}({\mathcal {N}})$ explizit hinschreiben kann (Physik: „kontravariante Größen“), ohne den Umweg über die Koeffizienten eines Vektorfeldes (Physik: „kovariante Größen“) ${\mathcal {A}}\in {\mathcal {X}}({\mathcal {N}})$ zu gehen mit

$A=g({\mathcal {A}},\cdot )\quad {\text{wobei}}\quad {\mathcal {A}}=a^{\mu }\partial _{\mu }$ .

Die Festlegung auf den Minkowskiraum, die man u.a. benötigt um „raumartige“ und „zeitartige“ Vektor- bzw. Tensorkomponenten zu unterscheiden, oder bei der Definition der Dualitätsoperation (siehe unten), ist also hier nicht erforderlich. Man könnte die Metrik auch frei wählen, dann sehen die Komponenten der Einsform

$A=a_{\mu }dx^{\mu }\quad {\text{(Viererpotential)}}$

nur anders aus, denn

$a_{\mu }=g_{\mu \nu }a^{\nu }\quad {\text{(Transformation zwischen Vektorfeld und Differentialform)}}$ .

Sei also ab hier die Mannigfaltigkeit der flache Minkowskiraum, das heißt o.B.d.A. ${\mathcal {N}}=M^{4}=(\mathbb {R} ^{4},g)$ . Dann ist das Vektorpotential gegeben durch

$A=-{\frac {\phi }{c}}\ \mathrm {d} t+a_{1}\ \mathrm {d} x+a_{2}\ \mathrm {d} y+a_{3}\ \mathrm {d} z\quad$ für das Vektorfeld $\quad {\mathcal {A}}=+{\frac {\phi }{c}}\ \partial _{t}+a^{1}\ \partial _{x}+a^{2}\ \partial _{y}+a^{3}\ \partial _{z}$ .

Die homogenen Maxwell-Gleichungen

Sei nun die äußere Ableitung von gegeben durch $F\in \Lambda ^{2}({\mathcal {N}})$ , also durch den sogenannten Feldstärketensor (Faradayzweiform):

$F=\mathrm {d} A\quad {\stackrel {\mathrm {d} }{\Rightarrow }}\quad \mathrm {d} F=\underbrace {\mathrm {d} ^{2}} _{=0}A=0\quad {\text{(homogene Maxwell-Gleichungen)}}$ .

Beeindruckend ist die Tatsache, dass die äußere Ableitung von immer verschwindet, unabhängig davon, wie aussieht. Das ergibt die sogenannte Eichfreiheit und begründet auch, warum die Einschränkung auf den Minkowskiraum die Allgemeinheit nicht verletzt. Da die Gleichungen jedoch ohne jeden physikalischen Input auskommen, folgt unmittelbar, dass die homogenen Maxwell-Gleichungen lediglich Folge der Geometrie des Raumes und des benutzten Formalismus sind (gleiches gilt ja auch für die Beziehung $\mathrm {d} ^{2}\equiv 0\,$ : eine geschlossene Differentialform ist ja noch weitgehend frei, nämlich bis auf das äußere Differential einer um einen Grad niedrigeren Form. ).

Die Materialgleichungen

Die Faradayzweiform lässt sich auch in den bereits bekannten Größen schreiben:

$F=E\wedge \mathrm {d} t+B\quad {\stackrel {*}{\Rightarrow }}*F=-{\sqrt {\frac {\mu _{0}}{\varepsilon _{0}}}}G\quad {\text{(Materialgleichungen)}}$ .

Die zu F duale^[4] Zweiform G heißt Maxwellzweiform und ist gegeben durch schon bekannten Größen, nämlich:

$G=D-H\wedge \mathrm {d} t$ .

In physikalischen Theorien entspricht F dem Feldstärketensor und G dessen dualem Tensor (siehe unten).

Die gesamten Maxwell-Gleichungen mit nur zwei Differentialformen

Definiert man nun eine Dreiform $J=\rho -j\wedge \mathrm {d} t\in \Lambda ^{3}({\mathcal {N}})$ ^[5], so ergibt deren äußere Ableitung

$\mathrm {d} J=0\quad {\text{(Kontinuitätsgleichung)}}\,.$

Das entspricht dem schon erwähnten Erhaltungssatz für die Gesamtladung.

Während nun die beiden homogenen Maxwell-Gleichungen (Maxwell I und II) durch die Aussage zusammengefasst werden können, dass die elektrischen bzw. magnetischen Felder bzw. durch eine einzige geschlossene Differentialform zweiter Stufe $\,F$ repräsentiert werden ( $\mathrm {d} F=0$ ), gilt für die verbleibenden inhomogenen Maxwell-Gleichungen III und IV die Aussage, dass die äußere Ableitung der dualen Form $G\,:=\,*F$ mit der Stromform identisch ist. Also

$\mathrm {d} (*F)=J\quad {\text{(inhomogene Maxwell-Gleichungen, III und IV)}}\,.$ .

Damit ist die Gesamtheit aller vier Maxwell-Gleichungen in mathematischer Kurzform durch nur zwei Differentialformen, und , ausgedrückt. (Insbesondere folgt aus der letzten Gleichung sofort auch die Kontuitätsgleichung, weil die zweimalige äußere Ableitung immer Null ergibt.)

Erneut spielt die Metrik keine direkte Rolle (indirekt ist sie sehr wichtig, z.B. bei der Definition der Dualität, die bei der Berechnung der Ladungen und Ströme aus den Feldern benötigt wird sowie bei der Angabe der expliziten Form der Lorentzinvarianz). Auch die Mannigfaltigkeit ${\mathcal {N}}$ ist beliebig, solange sie Dimension 4 hat. Letztlich ist aber physikalisch auch hier die Metrik wesentlich, nicht nur bei der gerade erwähnten Dualität. Sondern auch hier kommt es nicht allein auf die Vierdimensionalität der Mannigfaltigkeit an, sondern auch auf die Unterscheidung zwischen Raum- und Zeitkoordinaten (bzw. zwischen sogenannten raumartigen und zeitartigen Vektoren, Tensor- und Feldkomponenten), die sich ja mit Hilfe des metrischen Tensors ausdrücken. Dieser ist ja nicht gegeben durch $\mathrm {d} s^{2}=+c^{2}\mathrm {d} t^{2}+\mathrm {d} x^{2}+\mathrm {d} y^{2}+\mathrm {d} z^{2}\,,$ sondern z.B. durch $\mathrm {d} s^{2}=-c^{2}\mathrm {d} t^{2}+\mathrm {d} x^{2}+\mathrm {d} y^{2}+\mathrm {d} z^{2}\,.$ Man hat es also nicht mit einer $\mathbb {R} ^{4}$ -, sondern, wie schon gesagt, mit einer $\mathbb {M} ^{4}$ -Mannigfaltigkeit zu tun. Die Unterscheidung von „raumartigen“ und „zeitartigen“ Größen in der Metrik hängt auch mit dem Unterschied zwischen elektrischen und magnetischen Feldern zusammen. Obwohl die (insgesamt sechs) Feldkomponenten dieser Größen durch die Lorentz-Beziehungen ineinander transformiert werden können, ist die Charakterisierung eines Feldes als im Wesentlichen „elektrisch“ bzw. „magnetisch“ eine Invariante der Theorie, weil die Lagrange-Funktion, eine aus *F, F und J zusammengesetzte invariante Funktion, aus der sich die Bewegungsgleichungen (also die Maxwell-Gleichungen) berechnen lassen, im cgs-System im Wesentlichen gleich B²-E² ist. (Bemerkung: Ein Minkowski-Vektor ${\vec {v}}$ ist raumartig bzw. zeitartig bzw. lichtartig, je nachdem ob $(\mathrm {d} s)^{2}[{\vec {v}}]$ positiv bzw. negativ bzw. Null ist. Analog ist ein elektromagnetisches Feld im Wesentlichen magnetisch bzw. elektrisch bzw. wellenartig je nachdem ob die Lagrangefunktion, für ${\vec {J}}=0$ , positiv bzw. negativ bzw. Null ist.)

Abstrakte Integralformulierung und Interpretation

Diese abstrakte differentielle Formulierung der Maxwell-Gleichungen benutzt die Theorie der sogenannten alternierenden Differentialformen, insbesondere das sogenannte äußere Differential. Die zugehörige abstrakte Integralformulierung ergibt sich durch Anwendung des verallgemeinerten stokesschen Satzes aus dieser mathematischen Theorie: Man konzentriert sich dazu in der angegebenen Drei-Mannigfaltigkeit mit Minkowski-Metrik (z.B. eingebettet in den Raum $\mathbb {M} ^{4}\,$ ) besonders auf deren Rand $\partial V\,,$ eine geschlossene Zwei-Mannigfaltigkeit, und erhält:

$\left(\iiint _{V}\mathrm {d} F\equiv \right)\,\iint _{\partial V}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\;\;\;\subset \!\supset F=0$

für alle IMG class="text" style="width: 1.78ex; height: 2.17ex; vertical-align: -0.33ex;" alt="V" src="/svg/af0f6064540e84211d0ffe4dac72098adfa52845.svg">, sowie (mit $G=*F\,$ ):

$\left(\iiint _{V}\mathrm {d} G\equiv \right)\,\iint _{\partial V}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\;\;\;\subset \!\supset G=\iiint _{V}J\,.$

Dabei steht der eigentlich interessierende Teil hinter der Klammer und es wird durch das Zeichen $\;\;\iint _{\partial V}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\;\;\;\subset \!\supset$ im Sinne der Physik betont, dass das Integrationsgebiet $\partial V$ eine geschlossene Mannigfaltigkeit ist. Die erste der beiden angegebenen Gleichungen enthält das Faradaysche Induktionsgesetz und das Gesetz von der Nichtexistenz magnetischer Ladungen. In der letzten Gleichung ist das Maxwell-Ampèresche Gesetz und das Gesetz von Gauß enthalten. Beide Gesetze eines Paares gehören also jeweils zusammen. Das gaußsche Gesetz z.B. besagt in der hier gegebenen abstrakten Formulierung: Der Fluss der elektromagnetischen Form $cG$ durch den Rand der Mannigfaltigkeit V ist gleich der gesamten in V enthaltenen „Ladung“, wie sie sich aus der Stromform ergibt.

Die angegebene Eichfreiheit ergibt sich geometrisch daraus, dass man zu vorgegebenem Rand $\Gamma =\partial V$ viele verschiedene Mannigfaltigkeiten finden kann, die darin „hineinpassen“.

Besondere Formulierungen und Spezialfälle

Maxwell-Gleichungen für konstante Frequenzen ω in komplexer Schreibweise

Die in den Maxwell-Gleichungen auftretenden Feldvektoren sind im Allgemeinen nicht nur Funktionen des Ortes, sondern auch der Zeit, beispielsweise ${\vec {H}}(x,\,y,\,z,\,t)$ . In den partiellen Differentialgleichungen tritt dann neben den Ortsvariablen auch die Zeitvariable auf. Zur vereinfachten Lösung dieser Differentialgleichungen beschränkt man sich in der Praxis oft auf harmonische (sinusförmige) Vorgänge. Diese Darstellung ist für die praktische Feldberechnung, beispielsweise bei der Berechnung von elektromagnetischen Schirmen oder für die Antennentechnik, von wesentlicher Bedeutung.

Mit Hilfe der komplexen Schreibweise lässt sich die Zeitabhängigkeit bei harmonischen Vorgängen vermeiden, da sich der komplexe Zeitfaktor $e^{\mathrm {j} \,\omega \,t}$ dabei heraushebt und so aus den Maxwell-Gleichungen eine Helmholtz-Gleichung wird. Die in den Maxwell-Gleichungen auftretenden Feldgrößen sind dann komplexe Amplituden und nur noch Funktionen des Ortes. An Stelle der partiellen Differentiation nach der Zeit tritt die Multiplikation mit dem imaginären Faktor $\mathrm {j} \,\omega$ . Der Faktor $\omega$ wird auch als Kreisfrequenz bezeichnet.

Wie in der Elektrotechnik üblich, wird die imaginäre Einheit mit $\mathrm {j}$ bezeichnet (sie sollte nicht mit der häufig für die Stromdichte verwendeten Variable ${\vec {j}}$ verwechselt werden) – in der Mathematik und theoretischen Physik wird sie meist $\mathrm {i}$ geschrieben.

In komplexer Form – komplexe Größen sind zur Unterscheidung unterstrichen – lauten die Maxwell-Gleichungen in Differentialform:

${\vec {\nabla }}\cdot {\underline {\vec {D}}}=\rho$

${\vec {\nabla }}\cdot {\underline {\vec {B}}}=0$

${\vec {\nabla }}\times {\underline {\vec {E}}}=-\mathrm {j} \,\omega \,{\underline {\vec {B}}}$

${\vec {\nabla }}\times {\underline {\vec {H}}}={\underline {\vec {j}}}+\mathrm {j} \,\omega {\underline {\vec {D}}}=\left(\sigma +\mathrm {j} \,\omega \,\varepsilon \right)\,{\underline {\vec {E}}}$

Kovariante Formulierung der Maxwell-Gleichungen

In diesem Absatz wird, wie im übrigen Artikel, das SI-Einheitensystem verwendet. Dieses und die damit verbundenen Faktoren $\,\mu _{0}$ , $\varepsilon _{0}$ etc. empfinden viele Theoretiker gerade bei der kovarianten Formulierung der Elektrodynamik als unnatürlich und verwenden andere Systeme, etwa Gauß-Einheiten oder Heaviside-Lorentz-Einheiten, in denen die Grundgrößen der Elektrodynamik anders definiert werden. In der Literatur können deshalb, verglichen mit dieser Darstellung, Vorfaktoren wegfallen, hinzukommen oder an andere Stellen rücken.

Die Elektrodynamik, wie sie durch die Maxwell-Gleichungen beschrieben wird, ist im Gegensatz zur newtonschen Mechanik verträglich mit der speziellen Relativitätstheorie. Dazu gehört, dass die Maxwell-Gleichungen in jedem Inertialsystem gelten, ohne dass sich beim Wechsel des Bezugssystems ihre Form ändert. Das spielte historisch für die Entwicklung der Relativitätstheorie durch Albert Einstein eine wichtige Rolle.

Technischer formuliert sind die Maxwell-Gleichungen relativistisch kovariant oder forminvariant, das heißt, dass sie ihre Gestalt unter Lorentz-Transformationen nicht ändern.

Diese Eigenschaft ist den Maxwell-Gleichungen in der oben beschriebenen Form jedoch nicht ohne weiteres anzusehen. Es kann deshalb nützlich sein, durch eine Umformulierung der Theorie die Forminvarianz herauszuarbeiten, anders ausgedrückt: die Theorie „manifest kovariant“ zu schreiben.

Dazu ist es zweckmäßig, die oben auftretenden Größen ${\vec {E}}$ , ${\vec {B}}$ usw. durch Größen ausdrücken, die ein klar definiertes, einfaches Transformationsverhalten unter Lorentz-Transformationen haben, also durch Lorentz-Skalare, Vierervektoren und Vierer-Tensoren höherer Stufen.

Ausgangspunkt für diese Umformulierung bilden die elektromagnetischen Potentiale $\,\phi$ (skalares Potential) und ${\vec {A}}$ (Vektorpotential), aus denen man die elektrischen und magnetischen Felder durch

${\vec {E}}=-{\vec {\nabla }}\phi -\partial _{t}{\vec {A}}$
${\vec {B}}={\vec {\nabla }}\times {\vec {A}}$

erhält (siehe auch Elektrodynamik). Diese Größen lassen sich zu einem Vierervektor, dem Viererpotential

$A^{\mu }=\left({\frac {\phi }{c}},{\vec {A}}\right)$

zusammenfassen. Ebenso kann man aus Ladungsdichte $\,\rho$ und Stromdichte ${\vec {j}}$ die Viererstromdichte zusammensetzen, mit

$j^{\mu }=(c\rho ,{\vec {j}})$ .

Aus dem Viererpotential wird der elektrodynamische Feldstärketensor abgeleitet, dessen Komponenten bis auf Vorzeichen und konstante Vorfaktoren, die vom Einheitensystem abhängen, gerade die der elektrischen und magnetischen Felder sind. Er hat die Form

$F^{\alpha \beta }=\partial ^{\alpha }A^{\beta }-\partial ^{\beta }A^{\alpha }={\begin{pmatrix}0&-{\frac {E_{x}}{c}}&-{\frac {E_{y}}{c}}&-{\frac {E_{z}}{c}}\\{\frac {E_{x}}{c}}&0&-B_{z}&B_{y}\\{\frac {E_{y}}{c}}&B_{z}&0&-B_{x}\\{\frac {E_{z}}{c}}&-B_{y}&B_{x}&0\\\end{pmatrix}}$ .

Man definiert nun den Vierergradienten, die relativistische Form der Ableitung, als

$\partial ^{\alpha }=\left({\frac {1}{c}}{\frac {\partial }{\partial t}},-{\vec {\nabla }}\right)$ , also $\partial _{\alpha }=\left({\frac {1}{c}}{\frac {\partial }{\partial t}},+{\vec {\nabla }}\right)$ , sowie die Differentiale $\,\mathrm {d} x^{\alpha }=(c\mathrm {d} t,\mathrm {d} x,\mathrm {d} y,\mathrm {d} z)$ , die bei der Behandlung der Maxwell-Gleichungen im Artikel Differentialformen benötigt werden, der an dieser Stelle auch empfohlen wird.

Mit diesen Größen kann man die beiden inhomogenen Maxwell-Gleichungen im Vakuum durch die kovariante Gleichung

$\,\partial _{\alpha }F^{\alpha \beta }=\mu _{0}j^{\beta }$

ersetzen. Dabei wird, wie üblich, die einsteinsche Summenkonvention benutzt, das heißt, über doppelt auftretende Indizes in Produkten (hier $\alpha$ ) wird summiert. Ferner erfolgt wie üblich das Herauf- und Herunterziehen von Indizes mit dem metrischen Tensor

${\overset {\leftrightarrow }{\eta }}={\begin{pmatrix}+1&0&0&0\\0&-1&0&0\\0&0&-1&0\\0&0&0&-1\\\end{pmatrix}}$ .

Man beachte, dass wegen der Antisymmetrie des Feldstärketensors auch die Kontinuitätsgleichung (Verschwinden der Vierer-Divergenz) folgt

$\mu _{0}(\partial _{t}\rho +\operatorname {div} {\vec {j}})=\mu _{0}\partial _{\beta }j^{\beta }=\partial _{\alpha }\partial _{\beta }F^{\alpha \beta }=-\partial _{\alpha }\partial _{\beta }F^{\beta \alpha }=-\partial _{\beta }\partial _{\alpha }F^{\beta \alpha }=0$ .

Die beiden homogenen Maxwell-Gleichungen erhalten im Vakuum die manifest kovariante Form

$\,\partial _{\alpha }F_{\beta \gamma }+\partial _{\beta }F_{\gamma \alpha }+\partial _{\gamma }F_{\alpha \beta }=0$

Das wird auch häufig mit dem Levi-Civita-Symbol kompakter geschrieben als

$\varepsilon ^{\alpha \beta \gamma \delta }\partial _{\alpha }F_{\gamma \delta }=0$

oder

$\partial _{\alpha }{\tilde {F}}^{\alpha \beta }=0$

mit dem dualen Feldstärketensor

${\tilde {F}}^{\alpha \beta }:={\frac {1}{2}}\varepsilon ^{\alpha \beta \gamma \delta }F_{\gamma \delta },$

dessen Komponenten man auch aus denen von $\,F^{\alpha \beta }$ erhalten kann, indem man die Vektoren ${\vec {E}}/c$ durch ${\vec {B}}$ und ${\vec {B}}$ durch $-{\vec {E}}/c$ ersetzt. Also

${\tilde {F}}^{\alpha \beta }={\begin{pmatrix}0&-B_{x}&-B_{y}&-B_{z}\\B_{x}&0&{\frac {E_{z}}{c}}&-{\frac {E_{y}}{c}}\\B_{y}&-{\frac {E_{z}}{c}}&0&{\frac {E_{x}}{c}}\\B_{z}&{\frac {E_{y}}{c}}&-{\frac {E_{x}}{c}}&0\\\end{pmatrix}}$ .

Differentialformen ermöglichen eine besonders übersichtliche Darstellung der Maxwell-Gleichungen, die zudem automatisch kovariant ist. Dabei werden Viererpotential und Viererstromdichte durch die 1-Formen ${\vec {A}}$ und ${\vec {j}}$ dargestellt, der Feldstärketensor durch die 2-Form ${\vec {F}}=\mathrm {d} {\vec {A}}$ und sein Dual durch die 2-Form $*{\vec {F}}$ (das Symbol $\mathrm {d}$ steht bei Differentialformen für die Cartan-Ableitung). Die Maxwell-Gleichungen im Vakuum lauten dann

$*\mathrm {d} *{\vec {F}}=\mu _{0}{\vec {j}}$

und

$\mathrm {d} {\vec {F}}=0$ .

Maxwell-Gleichungen unter Berücksichtigung hypothetischer magnetischer Monopole

Magnetische Monopole treten in einigen GUT-Theorien als mögliche oder notwendige Bestandteile auf. Mit ihnen ließe sich die Quantelung der elektrischen Ladung erklären, wie Paul Dirac schon 1931 erkannte. Bislang wurden magnetische Monopole nur als Quasiteilchen beobachtet. Reale Teilchen als Monopole wurden noch nicht gefunden. Daher wird in den oben genannten Maxwell-Gleichungen auch angenommen, dass keine magnetischen Monopole (magnetische Ladungen) existieren.

Sollten in der Zukunft dennoch solche magnetischen Ladungen gefunden werden, so lassen sich diese in den Maxwell-Gleichungen problemlos berücksichtigen.

Setzt man $\rho _{m}$ für die Monopolladungsdichte, ${\vec {j}}_{m}=\rho _{m}{\vec {v}}_{m}$ für die Stromdichte und ${\vec {v}}_{m}$ für die Geschwindigkeit der sich bewegenden magnetischen Monopolladungen, so ändern sich nur zwei der vier oben genannten Gleichungen in differentieller Form zu

$\operatorname {div} {\vec {B}}=\rho _{m}\,\,.$

Interpretation: Die Feldlinien der magnetischen Flussdichte beginnen und enden in einer magnetischen Ladung.

$\operatorname {rot} {\vec {E}}=-\left({\frac {\partial }{\partial t}}{\vec {B}}+{\vec {j}}_{m}\right)\,.$

Interpretation: Sich zeitlich ändernde magnetische Flussdichten oder das Vorhandensein von magnetischen Stromdichten führen zu elektrischen Wirbelfeldern.

Die anderen beiden Gleichungen bleiben unverändert, während sich aber natürlich für die beiden neuen differentiellen (d.h. lokalen) Gleichungen auch neue integrale (d.h. globalen) Darstellungen ergeben, die aber ohne weiteres mit den Integralsätzen von Gauß und Stokes berechnet werden können.

Der Fall der verschwindenden Monopole $\rho _{m}=0$ führt wieder auf die bekannten, oben angegebenen Gleichungen zurück.

Maxwell-Gleichungen und Photonmasse

Die Photonmasse verschwindet gemäß der Maxwell-Gleichungen. Diese Gleichungen sind der Grenzfall m=0 der allgemeineren Maxwell-Proca-Gleichungen mit einer nicht negativen Masse der Austauschteilchen (im elektromagnetischen Fall der Photonen). Statt des Coulomb-Potentials ${\tfrac {q}{r}}$ bewirkt in der Maxwell-Proca-Theorie eine Punktladung das Yukawa-Potential ${\tfrac {q}{r}}\,\mathrm {e} ^{-m\,c\,r/\hbar }$ ,^[6] und hat nur noch eine Reichweite von etwa der Compton-Wellenlänge $\lambda _{m}=h/{m\,c}$ .^[7]

Historische Bemerkungen

Maxwell veröffentlichte seine Gleichungen 1865 (Eine dynamische Theorie des elektromagnetischen Feldes). In diesem System von ursprünglich zwanzig Gleichungen waren allerdings auch solche enthalten, die Definitionen enthielten und Gleichungen, die heute nicht mehr zu den eigentlichen Maxwellgleichungen gezählt werden (wie die Kontinuitätsgleichung aufgrund der Ladungserhaltung und Vorformen der Lorentzkraft). Bei den zwanzig Gleichungen wurden auch die jeweils drei Komponenten mitgezählt, die heute in einer Vektorgleichung zusammengefasst werden. Im Jahr 1873 findet sich in Maxwells A Treatise on Electricity and Magnetism in Band 2 (Teil 4, Kapitel 9) eine etwas abgewandelte Aufzählung, die aber noch weitgehend der Liste von 1865 entspricht. Zusätzlich brachte Maxwell seine Gleichungen in eine quaternionische Darstellung, eine damals besonders in Großbritannien beliebte Alternative zum Vektorkalkül. Im Zuge dessen hat Maxwell auch das magnetische Potenzialfeld ${\vec {\Omega }}$ und die magnetische Masse in seine Gleichungen eingeführt und diese Feldvariablen in die Gleichung für die elektromagnetische Kraft ${\vec {F}}$ eingefügt. Maxwell rechnete allerdings nicht direkt in dieser quaternionischen Notation, sondern behandelte den Skalarteil und den Vektorteil getrennt.

Die heute gängigen Vektor-Notationen wurden erst später von Oliver Heaviside und unabhängig Josiah Willard Gibbs und Heinrich Hertz auf der Grundlage der ursprünglichen Maxwell-Gleichungen von 1865 formuliert. Dabei schränkten sie auch das ursprüngliche System auf (in Vektornotation) vier Gleichungen ein. Diese sind einfacher zu lesen und in den meisten Fällen auch einfacher anzuwenden, weshalb sie auch heute noch üblich sind.

Maxwell-Gleichungen in natürlichen Einheitssystemen

In natürlichen Einheitensystemen fallen die Naturkonstanten weg.

Gaußsches Einheitensystem

Da das Gaußsche Einheitensystem auf dem CGS-System basiert, können nicht alle Naturkonstanten gekürzt werden.

In einer verbreiteten Version des gaußschen CGS-Systems lauten die Maxwell-Gleichungen:

Maxwell-Gleichungen im gaußschen cgs-System
Durchflutungsgesetz	${\vec {\nabla }}\times {\vec {H}}=4\pi {\frac {\vec {j}}{c}}+{\frac {1}{c}}\,{\frac {\partial {\vec {D}}}{\partial t}}$
Induktionsgesetz	${\vec {\nabla }}\times {\vec {E}}=-{\frac {1}{c}}{\frac {\partial {\vec {B}}}{\partial t}}$
Gaußsches Gesetz	${\vec {\nabla }}\cdot {\vec {D}}=4\pi \rho$
Gaußsches Gesetz des Magnetismus	${\vec {\nabla }}\cdot {\vec {B}}=0$

So werden die Maxwell-Gleichungen zum Beispiel im bekannten Lehrbuch von Jackson (das daneben noch das Internationale Einheitensystem (SI) benutzt) geschrieben. Daneben gibt es auch Versionen des gaußschen cgs-Systems, die eine andere Definition der Stromstärke benutzen und in denen das Durchflutungsgesetz lautet (z.B. im verbreiteten Lehrbuch von Panofsky und Phillips:)

${\vec {\nabla }}\times {\vec {H}}=4\pi {\vec {j}}+{\frac {1}{c}}\,{\frac {\partial {\vec {D}}}{\partial t}}$

Für die Potenziale wird im cgs-System gesetzt:

${\vec {E}}=-{\vec {\nabla }}\,\phi -{\frac {1}{c}}\,{\frac {\partial {\vec {A}}}{\partial t}}$ sowie ${\vec {B}}={\vec {\nabla }}\times {\vec {A}}\,.$

Ferner gilt

${\vec {D}}={\vec {E}}+4\pi {\vec {P}}$ und ${\vec {B}}={\vec {H}}+4\pi {\vec {M}}\,.$

Systematisches Transformationsverhalten (SI ↔ cgs)

Man kann in wenigen Zeilen das Transformationsverhalten zwischen SI- und cgs-Systemen systematisch beschreiben, obwohl die Transformationen schon deshalb nicht ganz trivial sind, weil das letztgenannte System drei Basisgrößen („Länge“, „Masse“, „Zeit“), das erstgenannte System aber vier davon hat (zusätzlich noch die „elektrische Stromstärke“). Im cgs-System üben zwei gleich geladene Punktmassen, deren Abstand beträgt, aufeinander die Coulomb-Kraft $q_{\mathrm {cgs} }^{2}/r^{2}$ aus, während im SI die gleiche Kraft $q_{\mathrm {SI} }^{2}/(4\pi \varepsilon _{0}r^{2})$ beträgt.

Es gilt also erstens: $q_{\mathrm {cgs} }=q_{\mathrm {SI} }/{\sqrt {4\pi \varepsilon _{0}}}\,.$ Nach einem ganz analogen Gesetz transformiert sich auch das elektrische Moment bzw. die elektrische Polarisation (elektrisches Moment pro Volumen) sowie die elektrische Stromdichte $j=\rho v.$ Die elektrische Feldstärke dagegen transformiert sich komplementär zu , weil das Produkt „Ladung mal Feldstärke“ invariant sein muss.
Zweitens gilt: $\textstyle E_{\mathrm {cgs} }=E_{\mathrm {SI} }\cdot {\sqrt {4\pi \varepsilon _{0}}}\,.$
Drittens ist: $\textstyle D_{\mathrm {cgs} }=D_{\mathrm {SI} }\cdot {\sqrt {\frac {4\pi }{\varepsilon _{0}}}}\,$ (weil im Vakuum $D_{\mathrm {SI} }=\varepsilon _{0}\,E_{\mathrm {SI} }\,,$ aber $D_{\mathrm {cgs} }=E_{\mathrm {cgs} }$ ist.)

Für die entsprechenden magnetischen Größen (erstens: das magnetische Moment bzw. die magnetische Polarisation $J=\mu _{0}M$ (Zusammenhang: $m=J\Delta V=\mu _{0}M\Delta V$ ), zweitens: die magnetische Feldstärke , drittens: die magnetische Induktion ) gelten ähnliche Gesetze, in denen $\mu _{0}$ an die Stelle von $\varepsilon _{0}$ tritt.

Sowohl das Durchflutungsgesetz als auch Faradays Induktionsgesetz koppeln aber elektrische und magnetische Größen. An dieser Stelle kommt die Lichtgeschwindigkeit ins Spiel, und zwar durch die fundamentale Beziehung $\varepsilon _{0}\mu _{0}\equiv 1/c^{2}\,.$

Wenn man z.B. das Durchflutungsgesetz betrachtet, das im SI folgendermaßen lautet: ${\operatorname {rot} }{\vec {H}}={\vec {j}}+{\frac {\partial {\vec {D}}}{\partial t}}\,,$ so erhält man im cgs-System die erste der gerade in der Tabelle angegebenen Gleichungen.

Heaviside-Lorentz-Einheitensystem

Da das Heaviside-Lorentz-Einheitensystem rationalisiert ist, fallen die $4\pi$ -Faktoren weg. Kombiniert mit dem Planck-Einheitensystem enthalten die Maxwell-Gleichungen keine Konstanten:

	HLE	kombiniert mit Planck-Einheiten
Durchflutungsgesetz	${\vec {\nabla }}\times {\vec {H}}={\frac {\vec {j}}{c}}+{\frac {1}{c}}\,{\frac {\partial {\vec {D}}}{\partial t}}$	${\vec {\nabla }}\times {\vec {H}}={\vec {j}}+{\frac {\partial {\vec {D}}}{\partial t}}$
Induktionsgesetz	${\vec {\nabla }}\times {\vec {E}}=-{\frac {1}{c}}{\frac {\partial {\vec {B}}}{\partial t}}$	${\vec {\nabla }}\times {\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}}$
Gaußsches Gesetz	${\vec {\nabla }}\cdot {\vec {D}}=\rho$	${\vec {\nabla }}\cdot {\vec {D}}=\rho$
Gaußsches Gesetz des Magnetismus	${\vec {\nabla }}\cdot {\vec {B}}=0$	${\vec {\nabla }}\cdot {\vec {B}}=0$

Literatur

Richard Becker, Fritz Sauter: Theorie der Elektrizität. Band 1 (Einführung in die Maxwellsche Theorie, Elektronentheorie, Relativitätstheorie). Teubner, Stuttgart 1969.
John David Jackson: Classical Electrodynamics. John Wiley, New York NY 1962 (3. edition. Pearson Addison-Wesley, San Francisco CA u.a. 1999, ISBN 0-471-30932-X; deutsch: 4. überarbeitete Auflage. de Gruyter, Berlin u.a. 2006, ISBN 3-11-018970-4).
Lew Landau, Jewgeni Lifschitz: Theoretische Physik. Band 2: Klassische Feldtheorie. 12. überarbeitete Auflage. Deutsch, Thun u.a. 1997, ISBN 3-8171-1327-7.
Wolfgang Panofsky, Melba Phillips: Classical Electricity and Magnetism. Addison-Wesley, Reading MA 1955 (2. edition. Dover, Mineola NY 2005, ISBN 0-486-43924-0).
Károly Simonyi: Theoretische Elektrotechnik. 10. Auflage. Barth, Leipzig u.a. 1993, ISBN 3-335-00375-6.

Anmerkungen

↑ Diese mikroskopischen Prozesse werden im Allgemeinen durch die Quantenmechanik beschrieben, wobei im Falle des Spinmagnetismus sogar die relativistische Form der Quantenmechanik, die sogenannte Dirac-Gleichung, herangezogen werden muss.
↑ ^a ^b Das eingeklammerte Doppelintegral ist Null, wenn die magnetische bzw. elektrische Induktion konstant bleibt. Auch in diesem Fall ergibt sich aber ein elektromotorischer Effekt, wenn in der betrachteten Zeit eine Änderung der Integrationsfläche ${\vec {A}}$ auftritt, die zu einer Lorentzkraft führt.
Siehe dazu die zweite der im unmittelbar folgenden Abschnitt angegebenen Gleichungen.
↑ In der Physikliteratur, und wenn aus dem Zusammenhang eindeutig erkennbar, wird die Leitungsstromdichte ${\vec {j_{\mathrm {l} }}}$ meist als ${\vec {j}}$ bezeichnet. In der Elektrotechnik ist die Bezeichnung ${\vec {J}}$ üblich.
↑ Die Dualitätsoperation vertauscht u.a. kovariante und kontravariante Vektor-Komponenten, sie hängt somit vom metrischen Tensor ab.
↑ An dieser Stelle wird in Kauf genommen, dass mit der gleich benannten Größe „magnetische Polarisation“ $,\equiv \mu _{0}M\,,$ verwechselt werden kann (siehe oben)
↑ mit der Konvention $\hbar = c = 1$ wird daraus ${\tfrac {q}{r}}\,\mathrm {e} ^{-m\,r}$
↑ mit der reduzierten Compton-Wellenlänge ${\lambda \!\!\!^{-}}=\hbar /{m\,c}$ vereinfacht sich das Yukawa-Potential zu ${\tfrac {q}{r}}\,\mathrm {e} ^{-r/{\lambda \!\!\!^{-}}}$

Basierend auf einem Artikel in:

Wikipedia.de