Feldlinie

Feldlinie (oder Kraftlinie) ist ein Begriff der Physik. Feldlinien sind gedachte oder gezeichnete Linien (i. A. gekrümmt), die die von einem Feld auf einen Probekörper ausgeübte Kraft veranschaulichen. Die an eine Feldlinie gelegte Tangente gibt die Kraftrichtung im jeweiligen Berührungspunkt an; die Dichte der Feldlinien gibt die Stärke des Feldes an.

Feld in der Umgebung eines Stabmagneten. Eisenfeilspäne auf Papier zeichnen die Richtung der Feldlinien nach. Die Eisenteilchen verklumpen.

Beispiele

Gravitationsfeldlinien veranschaulichen die Schwerkraft auf eine Probemasse. Auf der Erde – im Erdschwerefeld – sind diese Feldlinien praktisch Geraden, die Lotlinien oder Vertikalen, die man durch ein Schnurlot sichtbar machen kann.
Elektrische Feldlinien veranschaulichen die Coulombkraft auf elektrische Probeladungen. Sie beginnen auf positiven Ladungen und enden auf negativen Ladungen (oder jeweils in der Unendlichkeit).
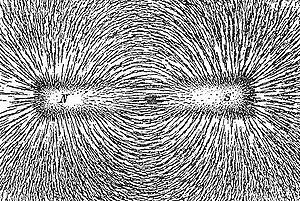
Magnetische Feldlinien veranschaulichen die magnetischen Kräfte auf Magnetpole. Sie sind in sich geschlossen, treten am Nordpol eines Magneten aus diesem aus und am Südpol in ihn ein. Allgemein zeigen sie stets in die Richtung, in die der Nordpol einer frei drehbaren Kompassnadel zeigt. Magnetische Dipole (z. B. Kompassnadeln) richten sich entlang den Feldlinien aus, da der eine Pol eine Kraft in Feldrichtung erfährt und der andere Pol eine Kraft in entgegengesetzter Richtung.

Die Gestalt und Dichte von magnetischen und elektrischen Feldlinien lassen sich mittels einfacher Demonstrationsexperimente sichtbar machen: Eisen wird – wie alle ferromagnetischen Materialien – durch ein Magnetfeld magnetisiert. Daher lagern Eisenspäne, z. B. auf einem Blatt Papier, sich aneinander an und bilden Ketten entlang der magnetischen Feldlinien. Ganz ähnlich wirkt das elektrische Feld auf Grießkörner in einer zähen, dielektrischen Flüssigkeit wie beispielsweise Rizinusöl. Die Körner werden durch das Feld elektrisch polarisiert und ordnen sich daher entlang der elektrischen Feldlinien an.

Eigenschaften

Der Betrag der Feldstärke ist proportional zur Feldliniendichte, und zwar nicht in der zweidimensionalen Darstellung, sondern im Raum: Die Zahl der Feldlinien, die durch eine orthogonal zu den Feldlinien orientierte Einheitsfläche hindurchtreten.
Feldlinien schneiden einander niemals. Wenn sich mehrere Felder in einem Punkt überlagern, geben die Feldlinien die Richtung der resultierenden Kraft an.
Feldlinien von Quellenfeldern (etwa Felder von elektrischen Ladungen, oder Gravitationsfelder) gehen von einem Punkt aus oder enden in einem Punkt.
Feldlinien von Wirbelfeldern (etwa Magnetfelder oder elektrische Felder, die durch sich ändernde Magnetfelder induziert werden) haben keinen Anfang und kein Ende, sondern sind geschlossene Linien.
Der Verlauf der Linien kann durch folgende Eselsbrücke anschaulich erläutert werden: Feldlinien „wollen“ immer möglichst kurz sein, stoßen sich aber gegenseitig ab.
Wenn die Feldlinien in einem bestimmten Gebiet gerade und parallel sind und eine konstante Dichte aufweisen, spricht man von einem homogenen Feld. Ist dies nicht der Fall, heißt das Feld inhomogen.
Wenn sich Verlauf und Dichte der Feldlinien im Laufe der Zeit nicht ändern, nennt man das Feld stationär.

Richtung (Orientierung) von Feldlinien

Die Feldlinien zeigen in Richtung der Feldstärke:

Beim Magnetfeld zeigen die Feldlinien in die Richtung, in die der Nordpol eines Elementarmagneten (Minikompass) zeigt. In der Umgebung eines Permanentmagneten verlaufen die Feldlinien daher vom Nord- zum Südpol.
Beim elektrischen Feld zeigen die Feldlinien in Richtung der Kraft, die auf eine positive Probeladung wirkt. In einem elektrostatischen (von Ladungen ausgehenden) Feld verlaufen sie also von der positiven zur negativen Ladung.

Begründung der Felddarstellung mittels Linien

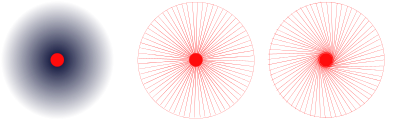
Unterschiedliche Darstellungsmöglichkeiten des Feldes um eine geladene Kugel, weit entfernt von anderen Ladungen. Das rechte Bild mit Linksdrall wird bei statischen Feldern nicht beobachtet, es dient nur zu Illustration.

Am Beispiel einer geladenen Kugel, die eine Kraftwirkung auf andere geladene Teilchen in der Umgebung ausübt, können verschiedene Möglichkeiten einer anschaulichen graphischen Darstellung des Feldes diskutiert werden.

Im linken Bild ist das schwächer werdende Feld durch geringere Farbsättigung dargestellt. Das hat den großen Vorteil, dass Fragen wie „Gibt es auch eine Kraft zwischen den Kraftlinien?“ erst gar nicht gestellt werden, weil die Fläche lückenlos bedeckt ist. Der Nachteil dieser Darstellung ist, dass es nicht einfach ist, dem Bild die Richtung der Kraft – das ist die Richtung der stärksten Änderung der Farbsättigung – zu entnehmen. Tiefergehende Fragen, etwa ob das Feld radialsymmetrisch (wie im mittleren Bild) oder z. B. mit Linksdrall wie im rechten Bild gestaltet ist, kann man mit der Farbsättigungsdarstellung überhaupt nicht beantworten.
Diese Feinheiten lassen sich in den Feldlinienbildern problemlos darstellen, allerdings mit dem Nachteil, dass oft Fragen gestellt werden wie „Gibt es nur diese Feldlinien oder liegen noch mehr davon dazwischen?“ oder „Gibt es weiter außen mehr Stellen ohne Feldlinien?“ oder „Spürt ein geladenes Teilchen auf einer tangentialen Bahn abwechselnd viel und weniger Kraft, wenn es die Feldlinien überquert?“
Die Frage, ob für eine geladene Kugel die mittlere oder z. B. die rechte Darstellung zutrifft, lässt sich nur experimentell oder durch Kenntnis besonderer "Regeln" (Feldlinien enden auf leitenden Flächen immer senkrecht) beantworten (Richtig ist die mittlere Darstellung). Bei der linken Darstellung stellt sich diese Frage überhaupt nicht.
Wie kann man zeichnerisch darstellen, ob ein Teilchen von der geladenen Kugel angezogen oder abgestoßen wird? Mit der Farbsättigungs-Darstellung ist dies nicht möglich. Die beiden anderen Darstellungen ermöglichen eine Unterscheidung durch Pfeilspitzen an den Linien.
Die Liniendarstellung bietet gewisse Vorteile im Zusammenhang mit der graphischen Lösung von Differentialgleichungen (Richtungsfeld).
Die Liniendarstellung ist einfacher zu zeichnen und drucktechnisch zu reproduzieren. Dies ist historisch sicherlich der wichtigste Grund, warum sie sich durchgesetzt hat.

Theoretischer Hintergrund

Eine Feldlinie bezeichnet einen Pfad entlang eines Vektorfeldes auf einer differenzierbaren Mannigfaltigkeit, beispielsweise entlang des elektrischen Feldes im Ortsraum. Da das Vektorfeld jedem Punkt der Mannigfaltigkeit einen Tangentialvektor zuordnet, Feldlinien aber, um sinnvoll von „Feldliniendichte“ sprechen zu können, zueinander Abstände haben müssen, wird klar, warum man das Konzept „Feldlinie“ nur zur qualitativen Veranschaulichung benutzt.

Typische Vektorfelder, wie sie Gegenstand der Elektrodynamik sind, lassen sich mit dem Zerlegungssatz in einen Gradienten- und einen Wirbelfeldanteil zerlegen. Die Feldlinien des Gradientenfeldes verlaufen zwischen den Senken und den Quellen, beim Wirbelfeld sind alle Feldlinien geschlossene Schleifen, die sich nicht kreuzen.

Formal charakterisiert man z.B. im elektrischen Feld die Feldlinien im Punkt $\vec{r}$ durch die Gleichung

$d\vec{s} \times \vec{E}(\vec{r}) = 0$

Wobei $d\vec{s}$ die infinitesimale Fortsetzung der durch den Punkt $\vec{r}$ verlaufenden Feldlinie darstellt. Dieser Gleichung genügen wegen der Definition des Kreuzprodukts alle Vektoren, die parallel zu den Feldlinien in diesem Punkt sind. Im zweidimensionalen Fall ( dz=E_z=0 ) reduziert sich diese Gleichung auf

$dy E_x - dx E_y = 0 \Longleftrightarrow \frac{dy}{dx} = \frac{E_y}{E_x}$

Das Feldlinienbild ermöglicht einen zwanglosen Zugang zum Gaußschen Integralsatz: Alle Feldlinien des Feldes $\vec E$ , die ihren Ursprung in einem Gebiet haben, das durch den Rand begrenzt ist, müssen entweder auch in diesem Gebiet enden oder durch den Rand hindurch stoßen. Folglich gilt:

$\int_V \operatorname{div} \vec E \; \mathrm dV = \oint_{S} \vec E \cdot \vec n\; \mathrm dS\,.$

In Worten: Die gesamte Quellenstärke des Vektorfeldes in einem Gebiet ist gleich groß wie der Fluss durch seine Randfläche. Daraus folgt sofort für kugelsymmetrische Probleme

$|\vec E(r)| \propto \frac 1 {4 \pi r^2},$

da sich die Feldlinien auf die Kugeloberfläche mit Radius „verteilen“. Diese Proportionalität findet sich z. B. im Gravitationsgesetz oder im Coulomb-Gesetz.

Siehe auch

Stromlinie

Basierend auf einem Artikel in Wikipedia.de