Dispersion

Farbzerlegung des Lichtes, oder allgemein die spektrale Zerlegung der Strahlung.

Die Dispersion tritt beim Durchgang der Strahlung durch Medien mit verschiedenem Brechungsindex auf und ist hierbei dadurch bedingt, daß der Brechungsindex von der Wellenlänge der Strahlung abhängig ist. Man nennt diese Form der Dispersion auch Brechungsdispersion, versteht aber meist unter Dispersion schlechthin die Brechungsdispersion. Auch die Beugung an einem Beugungsgitter oder einem Interferenzspektroskop bedingt eine Dispersion, die Beugungsdispersion genannt wird. Je nachdem, ob die Dispersion durch Brechung oder Beugung verursacht wurde, spricht man von einem Brechungsspektrum oder Beugungsspektrum, wobei das erstere meist Dispersionsspektrum genannt wird.

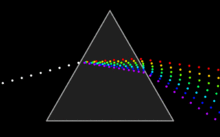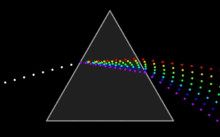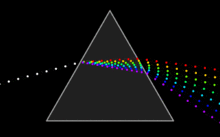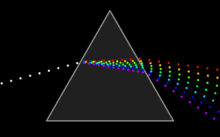
Bes. wirksam und physikalisch gut ausnutzbar ist die Dispersion beim Durchgang des Lichtes durch ein Prisma. Man nennt Prismen mit diesem Anwendungszweck deshalb Dispersionsprismen.

Strahlendurchgang für Licht von zwei Wellenlängen λ₁(rot) und λ₂(blau) durch ein Dispersionsprisma:
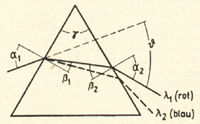
α₁ äußerer Einfallswinkel, α₂ äußerer Ausfallswinkel,
β₁ und β₂ innere Winkel,
θ Ablenkungswinkel,
γ brechender Winkel oder Prismenwinkel

Dispersion im Prisma erzeugt ein Farbspektrum

Der für die Dispersion wirksame Prismenwinkel γ heißt auch brechender Winkel. Der Ablenkungswinkel δ hat die Größe θ = (α₁ - β₁) + (α₂ - β₂).
Hierin ist der äußere Einfallswinkel α₁ für alle Wellenlängen gleich, während die inneren Winkel β₁ und β₂ sowie der äußere Ausfallswinkel α₂, vom Brechungsindex n_λ
nach dem Brechungsgesetz abhängen.
Berückschtigt man diese Abhängigkeit und weiterhin, entsprechend Abbildubg, daß β₁ + β₂ = γ ist, so erhält man θ = α₁ + α₂ - γ mit
.

Die Länge s des auf einer Auffangebene durch ein Prisma erzeugten Spektrums zwischen den Wellenlängen λ₁ und λ₂ ergibt sich aus der Differenz der Ablenkungswinkel γ und γ' der beiden Wellenlängen. Für verschiedene Glasarten sowie für künstliche und natürliche Kristalle - woraus im allgemeinen Dispersionsprismen hergestellt werden - nimmt γ mit zunehmender Wellenlänge im Bereich der normalen Dispersion, in dem man mit Dispersionsprismen arbeitet, kontinuierlich ab, während in den vorwiegend im Ultraviolett und Infrarot gelegenen Wellenlängenbereichen anomaler Dispersion außergewöhnliche und unstetige Abhängigkeiten des Ablenkwinkels γ von der Wellenlänge auftreten.

Der Differentialquotient des Ablenkungswinkels γ nach der Wellenlänge λ heißt Winkeldispersion ;
der Differentialquotient der Spektrumslänge s nach der Wellenlänge ist die Lineardispersion ,
 
welche die Ortsänderung der Wellenlänge in ienem ebenen Spektrum angibt und bei Prismenspektralapparaten auch noch von der Brennweite des verwendeten Abbildungsobjektivs oder Abbildungsspiegels abhängt.

Für die Winkeldispersion eines Prismas gilt allgemein .
Die Größe heißt Materialdispersion und kennzeichnet den Einfluß des Prismenmaterials auf die Dispersion.

Wird ein Dispersionsprisma im Minimum der Ablenkung durchstrahlt, dann ist α₁ = alpha;₂ und die Winkeldispersion D_w nimmt die einfache Form , an, worin b die Basislänge des Prismas und d die Breite des sie durchsetzenden Strahlenbündels ist.

Zur Angabe der Materialdispersion benötigt man die Funktion n(λ), also die Abhängigkeit des Brechungsindex von der Wellenlänge. Nach der empirischen Hartmannschen Dispersionsformel ist , die nur im Bereich der normalen Dispersion Gültigkeit hat.

Zur Untersuchung der anomalen Dispersion kann man sich des Verfahrens der gekreuzten Dispersion, bei dem zwei gleiche Spektren, senkrecht zueinander erzeugt werden (gekreuzte Spektren), bedienen.

Die Funktion n(λ) ist niemals linear, was zur Folge hat, daß im Dispersionsspektrum die Wellenlänge keine lineare Skala aufweist. Das sichtbare Dispersionsspektrum ist für alle praktisch ausgenutzten Prismensubstanzen (vor allem Flintglasarten) im Violetten und Blauen sehr auseinandergezogen, im Roten dagegen zusammengedrängt, da die Materialdispersion dieser Stoffe im Sichtbaren mit wachsender Wellenlänge abnimmt. Im nahen Infrarot nimmt die Dispersion wieder zu.

Die Brechungsdispersion bewirkt bei der Abbildung durch einfache Linsen, daß die von einem Dingpunkt kommenden Lichtstrahlen sich für die verschiedenen Wellenlängen in verschiedenen Bildpunkten vereinigen. Es tritt ein chromatischer Linsenfehler auf (Abbildungsfehler). Er kann dadurch beseitigt werden, daß zwei oder mehrere Linsen aus verschiedenen Glassorten zu einem Objektiv in geeigneter Weise vereinigt werden. Objektive, die vorwiegend diesen chromatischen Linsenfehler beseitigen, heißen daher Achromate.
Für die hierbei erforderliche Auswahl der geeigneten Glassorten benötigt man Angaben über die mittlere Dispersion des Glases, auch Grunddispersion D_g genannt. Es ist D_g = n_F - n_C ( wobei n = Brechungsindex für die Wasserstofflinie F bei 486,1 nm, n_C = Brechungsindex für die Linie C bei 656,3 nm).
Meist findet die Abbesche Zahl n Anwendung, definiert durch , wobei n_d = Brechungsindex für die Heliumlinie d bei 587,6 um ist.

Die Beugungsdispersion für ein ebenes Beugungsgitter wird durch die Winkeldispersion bzw. durch die Lineardispersion D_s =f - D_φ beschrieben, (m = Ordnung des Beugungsspektrums, g = Gitterkonstante, φ = Beugungswinkel, f = Brennweite des Abbildungsobjektivs). Sind die benutzten Beugungswinkel klein - was bei vielen Gitteranordnungen zutrifft -, so ist die Dispersion unabhängig von der Wellenlänge, also die Wellenlänge dem zugeordneten Beugungswinkel proportional. Das Gitterspektrum hat dann also eine lineare Wellenlängenskala. Es wird daher auch als Normalspektrum bezeichnet.
Für ein Konkavgitter ist in der Beziehung für D_s an Stelle der Brennweite f der Krümmungsradius g des Konkavgitters zu setzen.
Für Transmissionsstufengitter beträgt die Winkeldispersion bei kleinem Einfallswinkel ε wobei (n= Brechungsindex, D_m = Materialdispersion des benutzten Glases; d = Stufendicke, b = Stufenbreite).
Für Reflexionsstufengitter gilt die angenäherte d Beziehung .
Die Beugungsdispersion für Interferenzen an einer planparallelen Platte (Interferenzspektroskop) wird durch die Beziehung ausgedrückt, wobei ε der Austrittswinkel der Strahlen aus der Platte ist.

Auswirkungen

Die Dispersion der Phasengeschwindigkeit bestimmt die Dispersion der Gruppengeschwindigkeit.

Dispersion der Phasengeschwindigkeit

• Ein Prisma zerlegt Licht in sein Farbspektrum.
• Abbildungen mittels Linsen zeigen unerwünschte Farbränder, die durch Kombination von Linsen aus optischen Gläsern unterschiedlicher Dispersion korrigiert werden können (siehe Achromat und Apochromat).
• Auch magnetische Linsen etwa eines Elektronenmikroskops zeigen Dispersion in Abhängigkeit von der Geschwindigkeit der Elektronen. Gegenmaßnahmen sind eine schmale Energieverteilung der Elektronen, aus Feld- statt Glühemission, eine hohe Beschleunigungsspannung und eine kleine Apertur.

Dispersion der Gruppengeschwindigkeit

• Lichtimpulse in Glasfasern, welche beispielsweise in der optischen Datenübertragung eingesetzt werden, erfahren auf Grund der Dispersion der Gruppengeschwindigkeit eine Verbreiterung während der Übertragung. Je geringer die Dauer eines Lichtimpulses ist, desto breiter ist sein Frequenzspektrum und desto ausgeprägter ist die Änderung der Impulsform, besonders auf langen Übertragungsstrecken (siehe Dispersion in Lichtwellenleitern).
• Elektrische Kabel weisen je nach Frequenz aufgrund ihrer Isolierstoffe unterschiedliche Ausbreitungsgeschwindigkeiten auf, was sich z.B. bei der Zeitbereichsreflektometrie an verbreiterten reflektierten Impulsen zeigt. Der Effekt führt zu Laufzeitverzerrungen bei breitbandigen Signalen (zum Beispiel in Form von flacheren Impulsflanken) und kann durch geeignete Isolierstoffe vermieden werden.