Magnetisierung
| Physikalische Größe | |||||||
|---|---|---|---|---|---|---|---|
| Name | Magnetisierung | ||||||
| Formelzeichen | |||||||
| |||||||
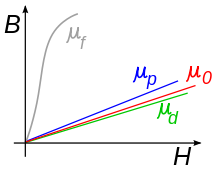
ferromagnetischen (μf),
paramagnetischen (μp) und
diamagnetischen Materialien (μd)
zu Vakuum (μ0)
Die Magnetisierung
ist eine physikalische
Größe zur Charakterisierung des magnetischen
Zustands eines Materials. Sie ist ein Vektorfeld,
das die Dichte von permanenten oder induzierten magnetischen Dipolen
in einem magnetischen Material beschreibt und berechnet sich als das magnetische Moment
pro Volumen
:
Die Magnetisierung beschreibt den Zusammenhang zwischen der magnetischen
Flussdichte
und der magnetischen
Feldstärke
:
Dabei ist
die magnetische
Feldkonstante und
die Permeabilität.
Diese Beziehung gilt im SI-System.
Im Gaußschen
CGS-System hingegen lautet die Definition: .
Im Folgenden wird durchgängig das SI verwendet.
In diamagnetischen
Materialien ist ,
die Magnetisierung ist dem erzeugenden Feld entgegengerichtet; in paramagnetischem
Material ist
,
Magnetisierung und Feld sind gleich gerichtet.
Die – praktisch wichtigste – ferromagnetische
Magnetisierung ist wesentlich größer als paramagnetische Magnetisierung ()
und nicht proportional der Feldstärke
(vgl. Skizze rechts), d.h.
ist hier keine Konstante, sondern selbst von
abhängig.
und
sind gleich gerichtet, aber nicht immer ganz parallel. Ein ferromagnetischer
Körper kann permanentmagnetisch
sein.
Jede Magnetisierung kommt durch die Ausrichtung von Elementarmagneten zustande. Da ein Körper nur endliche viele Elementarmagnete enthält, gibt es eine Sättigungsmagnetisierung, die auch in einem beliebig starken äußeren Feld nicht überschritten werden kann. Große praktische Bedeutung hat dies beim Ferromagnetismus (siehe Sättigung).
Beschreibung durch die Suszeptibilität
Die Magnetisierung kann auch durch die magnetische Feldstärke und die magnetische
Suszeptibilität
beschrieben werden:
Die Suszeptibilität
ist dimensionslos
und hat für diamagnetische Materialien einen (kleinen) negativen Wert, im
Extremfall eines Supraleiters
den Wert −1. Für paramagnetische Materialien hat sie einen kleinen positiven
Wert, für ferromagnetische Materialien ist sie sehr groß.
Magnetisierung eines Nagels
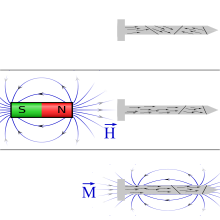
Ein Nagel aus Eisen, dessen magnetische Domänen anfänglich zufällige Richtungen haben, kann durch ein äußeres Feld magnetisiert werden. Dabei ändern Domänen ihre Richtung und manche Domänen vergrößern sich auf Kosten benachbarter Domänen. Insgesamt ergibt dies eine Magnetisierung, die ungefähr parallel zum äußeren Feld verläuft. Diese Umlagerung der magnetischen Domänen kann z.B. durch externe Stöße oder Vibrationen erleichtert werden. Aufgrund der ferromagnetischen Eigenschaften behält der Nagel seine Magnetisierung teilweise auch noch nach Entfernen des äußeren Feldes bei.
Magnetisierung in der Geologie/Mineralogie
Mineralien und Gesteine können bei ihrer Entstehung auf verschiedene Arten eine bleibende Magnetisierung erhalten, wobei das Magnetfeld der Erde jeweils die Polarisierung vorgibt:
- Thermisch remanente Magnetisierung (TRM): Die magnetische Ausrichtung der Mineralien in einer Schmelze wird durch Abkühlen unter die Curie-Temperatur fixiert.
- Chemisch remanente Magnetisierung (CRM): Mineralien, welche durch eine chemische Reaktion (z.B. Oxidation, Reduktion) zu magnetisierbaren Mineralien werden, richten sich bei der Umwandlung aus.
- Detritisch remanente Magnetisierung (DRM): magnetisierbare Mineralkörner richten sich bei der Sedimentation in der Wassersäule nach dem Magnetfeld der Erde aus und lagern sich mit dieser Ausrichtung auf dem Sediment ab.
- Postdetritisch remanente Magnetisierung (pDRM): Mineralien richten sich nach der Ablagerung im unverfestigten Sediment aus.
Siehe auch
Literatur
- Horst Stöcker: Taschenbuch der Physik. 4. Auflage. Harri Deutsch, Frankfurt am Main 2000, ISBN 3-8171-1628-4.
- Hans Fischer: Werkstoffe in der Elektrotechnik. 2. Auflage. Carl Hanser, München, Wien 1982, ISBN 3-446-13553-7.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 27.02. 2024