Dirac-Verteilung
Die Dirac-Verteilung, manchmal auch Punktverteilung, deterministische Verteilung, Einheitsmasse oder degenerierte Verteilung genannt, ist eine spezielle Wahrscheinlichkeitsverteilung in der Stochastik. Sie zählt zu den diskreten Wahrscheinlichkeitsverteilungen. Ihr Name folgt daher, dass sie aus dem Diracmaß abgeleitet wird. Sie ist meist nur von theoretischer Bedeutung und spielt eine wichtige Rolle in der Klassifikation der unendlich teilbaren Verteilungen.
Definition
Eine reelle Zufallsvariable
heißt Dirac-verteilt zum Punkt
,
in Symbolen
,
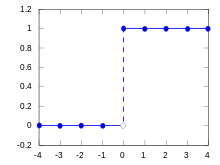
wenn sie die Verteilungsfunktion
besitzt. Die Verteilung von
ist also genau das Diracmaß im Punkt
,
das heißt für alle messbaren Mengen
gilt
Die Zufallsvariable nimmt insbesondere fast
sicher den Wert
an, worauf der Name deterministische Verteilung zurückzuführen ist.
Eigenschaften
Lagemaße
Erwartungswert, Modus
und Median
fallen alle zusammen und sind gleich dem Punkt
Streumaße
Varianz,
Standardabweichung
und Variationskoeffizient
fallen zusammen und sind alle gleich
Symmetrie
Die Dirac-Verteilung ist symmetrisch
um .
Höhere Momente
Die Momente sind gegeben durch
Entropie
Die Stochastik der Dirac-Verteilung ist 0.
Kumulanten
Die kumulantenerzeugende Funktion ist
.
Damit ist
und alle weiteren Kumulanten
sind gleich 0.
Charakteristische Funktion
Die charakteristische Funktion ist
Momenterzeugende Funktion
Die momenterzeugende Funktion ist
Reproduktivität, α-Stabilität und unendliche Teilbarkeit
Die Klasse der Dirac-Verteilungen ist reproduktiv, da die Summe Dirac-verteilter Zufallsvariablen wieder Dirac-verteilt ist, da für die Faltung
gilt. Des Weiteren sind Dirac-Verteilungen α-stabile
Verteilungen mit .
Teilweise werden aber Dirac-Verteilungen explizit von der Definition der
α-Stabilität ausgeschlossen. Außerdem sind Dirac-Verteilungen unendlich teilbar,
da
gilt.
Beziehung zu anderen Verteilungen
Die Dirac-Verteilung tritt meist als degenerierter Fall bei schlechter
Parameterwahl von anderen Verteilungen auf. Beispielsweise die
Bernoulli-Verteilung,
die Zweipunktverteilung
und die Binomialverteilung
alles Dirac-Verteilungen, wenn man
wählt. Des Weiteren ist auch die diskrete
Gleichverteilung auf einem Punkt eine Dirac-Verteilung.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 22.11. 2020