
Modulform
Der klassische Begriff einer Modulform ist der Oberbegriff für eine breite Klasse von Funktionen auf der oberen Halbebene (elliptische Modulformen) und deren höherdimensionalen Verallgemeinerungen (z. B. siegelsche Modulformen), der in den mathematischen Teilgebieten der Funktionentheorie und Zahlentheorie betrachtet wird. Der moderne Begriff einer Modulform ist dessen umfassende Neuformulierung in Termen der Darstellungstheorie (automorphe Darstellungen) und arithmetischen Geometrie (p-adische Modulformen). Klassische Modulformen sind Spezialfälle der sogenannten automorphen Formen. Neben Anwendungen in der Zahlentheorie haben sie zum Beispiel auch wichtige Anwendungen in der Stringtheorie und algebraischen Topologie.
Modulformen sind komplexwertige Funktionen mit bestimmten Symmetrien
(vorgeschriebenes Transformationsverhalten unter der Modulgruppe SL
oder deren Kongruenzuntergruppen). Sie hängen eng mit Gittern in der komplexen
Ebene, doppeltperiodischen Funktionen (elliptischen
Funktionen) und diskreten
Gruppen zusammen.
Geschichte
Die Anfänge der Theorie gehen auf Carl
Friedrich Gauß zurück, der Transformationen spezieller Modulformen unter der
Modulgruppe im Rahmen seiner Theorie des arithmetisch-geometrischen Mittels im
Komplexen betrachtete (ein Fundamentalbereich zu
findet sich in seinen Aufzeichnungen schon 1805).
Begründer der klassischen (rein analytischen) Theorie der Modulformen des 19.
Jahrhunderts sind Richard Dedekind,
Felix Klein, Leopold Kronecker,
Karl Weierstraß, Carl Gustav Jacobi, Gotthold Eisenstein und
Henri Poincaré.
Ein bekanntes Beispiel für die Anwendung von Modulformen in der
Zahlentheorie war der Satz
von Jacobi (Anzahl der Darstellungen einer Zahl durch vier Quadrate). Die
moderne Theorie der Modulformen entstand in der ersten Hälfte des zwanzigsten
Jahrhunderts durch Erich Hecke und Carl Ludwig Siegel, die Anwendungen in der Zahlentheorie verfolgten. Hier spielt
die Theorie der Hecke-Operatoren,
die im Raum der Modulformen wirken, und mit ihnen definierter Dirichletreihen (Hecke
L-Reihe) eine besondere Rolle. Modulformen in Termen der Darstellungstheorie
stammen von Robert Langlands (Langlands-Programm).
p-adische Modulformen treten zuerst bei Nicholas Katz und Jean-Pierre Serre auf. Modulformen spielten auch eine zentrale Rolle im Beweis der Vermutung
von Fermat (Modularitätssatz),
der wiederum ein Spezialfall der 2006 bewiesenen Serre-Vermutung ist,
die Modulformen mit Galoisdarstellungen der absoluten Galoisgruppe von
Zahlkörpern verbindet. Sowohl beim Beweis der Lösung des Gaußschen
Klassenzahlproblems durch Kurt Heegner als auch des letzten Teils der Weil-Vermutungen
(Riemann-Hypothese) und damit verbunden der Ramanujan-Vermutung
durch Pierre Deligne spielten Modulformen eine wichtige Rolle. Modulformen kodieren
häufig arithmetische Informationen der algebraischen Zahlkörper, sind aber viel
einfacher rechnerisch zugänglich, teilweise schon mit
Computeralgebra-Programmen, und die Anzahl linear unabhängiger Modulformen
bestimmten Typs ist beschränkt.
Modulformen spielten auch eine wesentliche Rolle beim Beweis von Maryna Viazovska (2016), dass das E8-Gitter in acht Dimensionen und das Leech-Gitter in 24 Dimensionen dichteste Kugelpackungen liefern (die Thetafunktionen dieser beiden Gitter sind Modulformen, siehe unten).
Elliptische Modulformen für SL2(ℤ)
Definition
Es sei
die obere Halbebene, d. h. die Menge aller komplexen Zahlen mit positivem Imaginärteil.
Für eine ganze Zahl
heißt eine holomorphe
bzw. meromorphe
Funktion
auf der oberen Halbebene eine holomorphe bzw. meromorphe elliptische
Modulform vom Gewicht
zur Gruppe
(Modulgruppe), wenn sie
-
für alle
und
mit
- erfüllt und
- „holomorph bzw. meromorph im Unendlichen“ ist. Das bedeutet, dass die Funktion
-
mit
- (die Fourier- oder q-Entwicklung von f) holomorph bzw. meromorph an der
Stelle
ist.
Ist
meromorph und
,
so nennt man
eine Modulfunktion. Modulfunktionen haben ein besonders einfaches
Verhalten unter der Modulgruppe:
Holomorphe Modulfunktionen sind uninteressant, da die einzigen holomorphen
Modulfunktionen die konstanten Funktionen (Satz
von Liouville) sind. Man nennt die holomorphen Modulformen auch ganze
Modulform. Verschwindet eine solche ganze Modulform darüber hinaus im
Unendlichen
(in der Spitze, englisch cusp,
),
so nennt man sie Spitzenform.
Genauer verschwindet eine Spitzenform vom Gewicht k für
wie
.
Die j-Funktion ist dagegen eine in der oberen Halbebene holomorphe Modulfunktion
bis auf einen einfachen Pol in der Spitze, also ein Beispiel für Meromorphie.
Aus der Definition folgt, dass eine Modulform für ungerades
identisch verschwindet.
Die in der Definition der Modulform verwendeten speziellen Möbiustransformationen bilden die Modulgruppe [1]
Die Modulgruppe wird auch mit
bezeichnet. Die Modulformen sind durch ihr einfaches Transformationsverhalten
gegenüber der Modulgruppe gekennzeichnet. Die Modulgruppe bildet die Obere
Halbebene
auf sich ab und wird durch die Erzeugenden
erzeugt (diese sind geometrisch eine Spiegelung an einem Kreis (Inversion) und
eine Translation):
Das Verhalten der Modulform vom Gewicht
unter diesen Erzeugenden ist:
und aus letzterer Gleichung ergibt sich, dass die Modulform periodisch ist.
Daher ist die Fourierentwicklung
für
wohldefiniert und holomorph bzw. meromorph. Mit den Fourierkoeffizienten
hat man die Fourierreihe (auch q-Entwicklung genannt):
Wobei m die Ordnung des Pols von
in der Spitze
genannt wird (Imaginärteil von
gegen Unendlich). Die Modulform ist bei negativen Fouriergliedern meromorph in
der Spitze. Bei einer Spitzenform verschwindet
bei
(
),
das heißt die nichtverschwindenden Fourierkoeffizienten beginnen bei einem
positiven
,
der dann Ordnung der Nullstelle von
in der Spitze genannt wird.
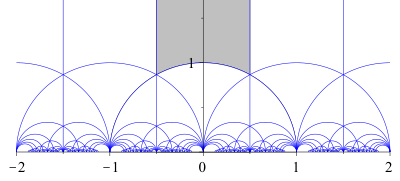
In der komplexen Ebene ist eine Modulform durch ihre Werte im
Fundamentalbereich
definiert, der in der nebenstehenden Abbildung blau gefärbt ist. Es ist ein
Dreieck mit einer Spitze im Unendlichen. Jedes der durch Geraden oder Kreise
begrenzten fundamentalen Dreiecke entsteht durch Anwendung von Operationen der
Modulgruppe auf den Fundamentalbereich. Die Anwendung der Modulgruppe lässt sich
beliebig fortsetzen und ergibt eine immer feinere Einteilung, die aber in der
Abbildung an einem bestimmten Punkt abgebrochen wurde.
Die Abbildung stellt die berühmte Modulfigur dar, die zum Beispiel von M. C. Escher in mehreren Graphiken künstlerisch dargestellt wurde.
Beispiele und Zusammenhang mit Gittern
Die einfachsten Beispiele für ganze Modulformen vom Gewicht
sind die sogenannten Eisensteinreihen
,
für eine Modulfunktion die j-Funktion
oder absolute Invariante und für eine Spitzenform die Diskriminante
.
Die Modulgruppe hat die wichtige Eigenschaft, dass sie Gitter in der
komplexen Ebene auf sich abbildet. Diese Gitter werden von zwei komplexen Zahlen
mit
aufgespannt:
.
Sie lassen sich als Parallelogramme in der komplexen Zahlenebene darstellen.
Eine andere Basis des Gitters, gegeben durch zwei komplexe Zahlen ,
spannt genau dann dasselbe Gitter auf, wenn die beiden Basen durch ein Element
der Modulgruppe ineinander transformiert werden (das folgt aus der Bedingung,
dass die Determinante gleich 1 ist und der Ganzzahligkeit):
Setzt man
ergibt sich die oben angegebene Transformationsformel
über eine Möbiustransformation.
Eisensteinreihen sind auf natürliche Weise auf diesen Gittern definiert:
Oder mit
(also einem
aus der oberen Halbebene):
.
Da das Gitter invariant unter der Modulgruppe ist, gilt dies auch für die
Eisensteinreihen. Sie sind ganze Modulformen vom Gewicht ,
wobei
gerade ist (sonst würde die Modulform identisch verschwinden, da über alle
Gitterpunkte
summiert wird, worunter sich auch
befindet). Damit die Reihen konvergieren muss auch
größer als 2 sein.
Unter den Erzeugenden der Modulgruppe transformiert die Eisensteinreihe:
Der Zusammenhang mit Gittern ergibt auch eine Verbindung von Modulformen zu
Elliptische
Funktionen, die als doppeltperiodische, meromorphe Funktionen auf einem
solchen Gitter definiert sind (werden die Seiten des Gitters miteinander
identifiziert ergibt sich ein Torus mit topologischem Geschlecht ,
die Riemannsche
Fläche der elliptischen Funktionen). Am einfachsten wird das durch
Betrachtung der Weierstraßschen
℘-Funktion deutlich. Meromorphe Modulformen vom Gewicht 0 sind auf den
Isomorphieklassen der den elliptischen Funktionen zugrundeliegenden Gittern
definiert. Die j-Invariante einer elliptischen Funktion kennzeichnet diese
Isomorphieklassen, die damit von dieser Funktion der oberen Halbebene eindeutig
parametrisiert werden. Sie ist eine Modulform vom Gewicht 0 und lässt sich als
rationale Funktion aus Eisensteinreihen vom Gewicht 4 und 6 bilden, mit der modularen
Diskriminante im Nenner, einer Modulfunktion vom Gewicht 12 (sie steht
wiederum mit der Dedekindsche
η-Funktion in Verbindung). Die j-Funktion hat viele interessante
Eigenschaften, die sie wichtig für die Zahlentheorie (Konstruktion algebraischer
Zahlkörper) und Gruppentheorie (die Fourierkoeffizienten ihrer q-Entwicklung
stehen mit Darstellung der Monstergruppe in Verbindung, moonshine)
machen.
Der Zusammenhang von Modulformen und Elliptischen Kurven setzt sich auch bei über Zahlkörpern definierten elliptischen Kurven fort, wo der oben erwähnte Modularitätssatz gilt, dass alle über Zahlkörpern definierten elliptischen Kurven sich durch Modulformen parametrisieren lassen (aus diesem Satz folgt die Fermatvermutung nach Andrew Wiles und anderen).
Ein weiteres Beispiel für Modulformen liefern Thetafunktionen, die auf Gittern definiert sind.
Beispielsweise liefert die Thetafunktion zu einem geraden, unimodularen
Gitter
im
:
eine Modulform vom Gewicht .
Zum Beweis wird für das Verhalten unter Inversion die Poissonsche
Summenformel benutzt. Unimodular bedeutet, dass die Gitterdiskriminante
gleich 1 ist und gerade, dass die Quadrate der Längen der Vektoren des Gitters
alle gerade sind. Beispiele solcher Gitter (deren Dimension n durch 8 teilbar
sein muss) sind das Leech-Gitter
(n=24, als eines von 24 Niemeier-Gittern) und das Gitter des Wurzelsystems der
speziellen Liegruppe
(n=8). Im Fall n=8 ist sie also eine Modulform vom Gewicht 4, davon gibt es aber
nur eine, die Eisenstein-Reihe vom Gewicht 4.
Vektorräume der Modulformen
Für ungerades
ist stets
,
die folgenden Aussagen gelten daher für gerades
.
Summen und Produkte von Modulformen sind wieder Modulformen. Die Modulformen
vom Gewicht k bilden einen -Vektorraum,
ebenso die ganzen Modulformen und auch die Spitzenformen.
Bezeichnet man diese Vektorräume mit
und
,
so gilt:
Für die Dimension dieser Vektorräume gilt (k sei eine positive gerade ganze Zahl):
Da durch die Multiplikation mit der Spitzenform
(Diskriminante)
vom Gewicht 12 ein Isomorphismus von
nach
gegeben ist, gilt
Die Modulräume
für
sind eindimensional und werden erzeugt von den
und für
zweidimensional, erzeugt von
,
mit den Eisensteinreihen
.
Allgemein kann man zeigen, dass alle Elemente von
durch Polynome in
erzeugt werden:
mit Konstanten .
Es ist aber häufig nützlicher, Basen von Eigenformen der Hecke-Operatoren zu
verwenden (Atkin-Lehner-Theorie).
Hans Petersson führte das Petersson-Skalarprodukt im Raum der Spitzenformen ein und machte diese damit zu einem Hilbertraum. Man kann mit dem Satz von Riemann-Roch Aussagen über die Dimension der Vektorräume der Spitzenformen machen. Eisensteinreihen sind bezüglich des Petersson-Skalarprodukts orthogonal zu den Spitzenformen. [2]
Ein Grund für die Nützlichkeit von Modulformen in unterschiedlichsten Anwendung ist, dass sie zwar häufig unterschiedliche Beschreibungen in den verschiedensten Anwendungen haben, man aber sofort Verbindungen unter den Modulformen findet, da die Vektorräume von relativ kleiner Dimension sind.
Kongruenzuntergruppen
Statt für
werden Modulformen auch für diskrete Untergruppen dieser Gruppe betrachtet,
insbesondere für (N ist eine positive ganze Zahl) die sogenannten Kongruenzuntergruppen
der Modulgruppe:
Die Zahl
heißt die Stufe der zugeordneten Modulformen.
heißt auch die Hauptkongruenzgruppe der Stufe
.
Jede Untergruppe von
,
die die Hauptkongruenzgruppe für eine Stufe N als Untergruppe enthält, wird
Kongruenzuntergruppe genannt.
Bisweilen betrachtet man auch die Kongruenzuntergruppe:
die eine Mittelstellung einnimmt zwischen
(mod N äquivalent zu oberer Dreiecksmatrix) und
(mod N äquivalent zur Einheitsmatrix). Es gilt
und außerdem gilt
.
Der Index der Kongruenzuntergruppen als Untergruppen von
ist endlich und lässt sich explizit angeben. So ist:
Die Modulformen zur Kongruenzuntergruppe
und
haben Fourierentwicklungen in
;
die von
für
nicht unbedingt, da die Matrix (a=d=1, b=1, c=0) in der Transformationsmatrix
nicht dazugehört (sie haben eine Fourierentwicklung in
).
Es lässt sich aber immer zu einer Modulform für
eine solche für
zuordnen (die eine Fourierentwicklung in
hat). Auch gibt es für Kongruenzuntergruppen kein so einfaches Kriterium für
Spitzenformen (der konstante Fourierterm muss nicht unbedingt verschwinden wie
bei der vollen Modulgruppe). Neben Modulformen mit Transformationsverhalten wie
bei der vollen Modulgruppe diskutiert werden auch solche mit erweitertem
Transformationsverhalten (Multiplikation mit einem Dirichlet-Charakter)
betrachtet.
Mit diesen Kongruenzuntergruppen kann man die Quotientenräume wie
bilden, die durch Hinzunahme endlich vieler Punkte (Cusp, Spitzen der
Kongruenzuntergruppe) in der erweiterten oberen Halbebene [3]
kompaktifiziert werden, der entsprechende kompaktifizierte Quotientenraum heißt
dann
.
Entsprechend spricht man bei der Kongruenzuntergruppe
von
bzw.
und bei
von
.
Nach Kompaktifizierung erhält man kompakte Riemannsche
Flächen unterschiedlichen topologischen Geschlechts
.
Die verschiedenen
heißen auch Modulkurven.
Zum Beispiel ist
die Riemannsphäre (Geschlecht 0) mit 12 Spitzen, die wie das Ikosaeder angeordnet sind.
ist die Klein-Quartik
mit Geschlecht 3 und 24 Spitzen.
ist die klassische Modulkurve und wird auch häufig einfach nur als Modulkurve
bezeichnet.
Modulkurven parametrisieren Äquivalenzklassen von elliptischen Kurven
abhängig von der Art der Kongruenzuntergruppe und lassen sich rein algebraisch
definieren und so auch über anderen Körpern als
betrachten. Sie sind in der arithmetischen Geometrie von Bedeutung.
Verallgemeinerungen, automorphe Formen
Modulfunktionen lassen sich durch Erweiterung der Art des Transformationsverhaltens und für andere Gruppen als die Modulgruppe verallgemeinern.
Zunächst wurden oben nur Modulformen zu ganzzahligem Gewicht k betrachtet, es
gibt aber auch solche zu rationalen Werten, die auch eine Rolle in der
Zahlentheorie spielen, so benutzte Jerrold Tunnell Modulformen zum Gewicht
bei der Lösung des Problems kongruenter
Zahlen.
Beispielsweise kann man Funktionen betrachten, die sich durch Multiplikation mit einem automorphen Faktor transformieren:
mit dem automorphen Faktor ,
wobei
.
Das sind Beispiele für automorphe Funktionen. Ein Beispiel ist die Dedekindsche Etafunktion.
In der algebraischen Zahlentheorie werden auch häufig
Modulfunktionen zur Kongruenzuntergruppe
betrachtet mit einem automorphen Faktor, der mit dem Dirichlet-Charakter
gebildet wird (Modulformen vom Gewicht
,
Nebentypus
und Stufe
):
Sie sind für
in der oberen Halbebene definiert und holomorph in der Spitze.
Automorphe Formen sind für topologische Gruppen
(Lie-Gruppe) definiert und
deren diskrete Untergruppen
.
Das entspricht im Fall der Modulformen für die Modulgruppe
der Modulgruppe selbst als diskreter Untergruppe der Liegruppe
oder den Kongruenzuntergruppen als diskreten Untergruppe der Modulgruppe. Das
Transformationsgesetz wird hier allgemein mit Automorphiefaktoren definiert.
Automorphe Formen sind Eigenfunktionen bestimmter Casimir-Operatoren von
(das entspricht bei den Modulfunktionen der Tatsache, dass diese analytische
Funktionen in zwei Dimensionen sind, die die Laplacegleichung erfüllen, was dem
Casimir-Operator für
entspricht) und erfüllen wie die Modulformen bestimmte Wachstumsbedingungen. Sie
wurden schon im 19. Jahrhundert für Fuchssche
Gruppen (diskrete Untergruppen von
)
von Henri Poincaré betrachtet und in der Zahlentheorie Anfang des 20. Jahrhunderts von
David Hilbert
(Hilbertsche Modulformen für total reelle Zahlkörper [4]
zur allgemeinen linearen Gruppe
über dem Ring der ganzen Zahlen des Zahlkörpers, definiert als Modulform auf dem
-fachen
Produkt der oberen Halbebene, mit
dem Grad von
über den rationalen Zahlen).
Ein weiteres Beispiel automorpher Formen in mehreren komplexen Variablen sind Siegelsche Modulformen, die im Siegelschen Halbraum definiert sind und autormorphe Formen zur Symplektischen Gruppe sind. Sie spielen eine ähnliche Rolle für die Parametrisierung abelscher Varietäten wie Modulformen für die Parametrisierung von Elliptischen Funktionen (als jeweilige Modulräume) und wurden von Carl Ludwig Siegel ursprünglich in der Theorie quadratischer Formen betrachtet.
Auch Jacobiformen sind automorphe Funktionen in mehreren Variablen, zu ihnen gehört zum Beispiel die Weierstraßsche ℘-Funktion und die Jacobische Thetafunktion.
Automorphe Formen spielen eine wesentliche Rolle im Langlands-Programm, wo algebraische Gruppen in einem zahlentheoretischen Kontext betrachtet werden (als algebraische Gruppen über dem Adelring eines algebraischen Zahlkörpers) und deren Darstellungstheorie eine besondere Rolle spielt.
Weitere Beispiele von Erweiterungen des Konzepts von Modulformen sind die
Mock-Thetafunktionen von S. Ramanujan bzw. Mock-Modulformen. Sie sind selbst keine Modulformen, lassen
sich aber durch Addition einer nicht-holomorphen Komponente (Schatten der
Mock-Modulform genannt) zu einer Modulform vervollständigen und fanden
spektakuläre Anwendung in der Theorie der Partitionen durch Ken Ono, Jan Hendrik Bruinier und Kathrin Bringmann.
Sie stehen nach Sander Zwegers in Zusammenhang mit Maaß-Formen bzw. Maaß-Wellenformen
von Hans Maaß, nicht-analytischen automorphen Formen, die als Eigenfunktionen des
invarianten (hyperbolischen) Laplace-Operators zum Gewicht
sind. Mock-Modulformen sind der holomorphe Anteil einer schwachen
Maaßform, wobei sich das schwach auf die verlangten Wachstumsbedingungen
bezieht.
Anmerkungen
- ↑ Manche Autoren bezeichnen auch die projektive spezielle lineare Gruppe PSL(2, Z) als Modulgruppe, in der Matrizen A und −A identifiziert werden. Sie ist der Quotient von SL(2, Z) mit seinem Zentrum Z = (1, −1).
- ↑ Kilford: Modular forms. 2008, S. 70. Manchmal wird das auch zur Definition der Eisensteinreihen verwendet.
- ↑
Die erweiterte obere Halbebene besteht aus
,
und
. Die rationalen Zahlen erscheinen, da für
der Orbit durch Wirkung der Kongruenzuntergruppen im Unendlichen durch
im Unendlichen geht.
- ↑
Erzeugt als Erweiterung der rationalen Zahlen
durch Adjunktion einer Wurzel
eines ganzzahligen Polynoms mit
reellen Wurzeln.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 01.09. 2021