Doppler-Effekt

Änderung der Wellenlänge durch Doppler-Effekt

Änderung der Wellenlänge bei Bewegung der Schallquelle

Der Doppler-Effekt (selten Doppler-Fizeau-Effekt) ist die zeitliche Stauchung bzw. Dehnung eines Signals bei Veränderungen des Abstands zwischen Sender und Empfänger während der Dauer des Signals. Ursache ist die Veränderung der Laufzeit. Dieser rein kinematische Effekt tritt bei allen Signalen auf, die sich mit einer bestimmten Geschwindigkeit, meist Lichtgeschwindigkeit oder Schallgeschwindigkeit, ausbreiten. Breitet sich das Signal in einem Medium aus, so ist dessen Bewegungszustand zu berücksichtigen.

Bei periodischen Signalen erhöht bzw. vermindert sich die beobachtete Frequenz. Das betrifft sowohl Tonhöhen als auch Modulationsfrequenzen, z.B. den Wechsel der Töne eines Martinhorns („tatü…taataa“). Bei geringen Geschwindigkeiten im Verhältnis zur Ausbreitungsgeschwindigkeit gibt dieses Verhältnis zugleich die relative Frequenzänderung ${\frac {\Delta f}{f}}$ an. Bei reflektiertem Signal, wie beim Radar-Doppler und Ultraschall-Doppler, verdoppelt sich mit der Laufzeit auch die Doppler-Verschiebung $\Delta f$ .

Geschichte

Porträt von Christian Doppler

Der Doppler-Effekt wurde bekannt durch Christian Doppler, der im Jahre 1842 Astronomen davon zu überzeugen versuchte, dass dieser Effekt die Ursache dafür sei, dass bei Doppelsternen zwischen den beiden Partnersternen Farbunterschiede erkennbar sind. Nach seiner Meinung kreisen diese Sterne so schnell umeinander, dass die Farbe des gerade vom Beobachter hinweg bewegten Sterns mit einer Rotverschiebung wahrgenommen wird, während die Farbe des zulaufenden Sterns in den blauen Bereich des Spektrums verschoben ist. Dieser Effekt konnte nach dem Tode Dopplers tatsächlich durch die Vermessung von Spektrallinien nachgewiesen werden. Er ist aber zu gering, um wahrnehmbare Farbunterschiede zu erklären. Die tatsächliche Ursache für mit dem Auge erkennbare Farbunterschiede zwischen Sternen sind deren Temperaturunterschiede.

Zur Erklärung des Effektes stellte Doppler ein Gedankenexperiment mit der Laufzeit von Wasserwellen an, die im Minutentakt von einem fahrenden Boot aus erzeugt werden. Daraus leitete er auch eine mathematische Beschreibung ab. Ein Verdienst von Doppler ist die Erkenntnis, dass die Endlichkeit der Lichtgeschwindigkeit auch eine Änderung der Wellenlänge des von bewegten Quellen eintreffenden Lichts bewirken muss. Im französischen Sprachraum wird dies oft Armand Fizeau (1848) zugesprochen.

Die Endlichkeit der Lichtausbreitung war bereits 180 Jahre zuvor von Ole Rømer gedeutet worden. Rømer interessierte sich für die Eignung der Jupitermonde als Zeitgeber zur Lösung des Längengradproblems. Die Verfinsterungen des Jupitermondes Io waren mit einer Frequenz von 1/1,8d bekannt, die gut als Zeitgeber geeignet wären. Allerdings stellte Rømer fest, dass sich diese Frequenz verringert, wenn sich die Erde auf ihrer Umlaufbahn um die Sonne gerade vom Jupiter wegbewegt. Mit $v_\text{Orbit, Erde} = 30\,\mathrm{km/s}$ ist das $v/c=1/10\,000$ und verlängert die Zeit von Io-Finsternis zu Io-Finsternis gerade um 1,8d/10 000, also ca. 1/4 Minute. Diese Verzögerung summierte sich nach 40 Umläufen von Io um Jupiter auf 10 Minuten, die Rømer für den 9. November 1676 vorhersagte. Auch wenn Rømer tatsächlich an der Frequenzänderung der Io-Finsternisse interessiert war: Er interpretierte diese 10 Minuten viel einfacher als die Verzögerung, die das Licht für die entsprechend längere Wegstrecke benötigt hatte.

Für die Schallwellen hat der Naturforscher Christoph Buys Ballot im Jahre 1845 den Doppler-Effekt nachgewiesen. Er postierte dazu mehrere Trompeter sowohl auf einem fahrenden Eisenbahnzug als auch neben der Bahnstrecke. Im Vorbeifahren sollte jeweils einer von ihnen ein G spielen und die anderen die gehörte Tonhöhe bestimmen. Es ergab sich eine Verschiebung von einem Halbton, entsprechend einer Geschwindigkeit von 70 km/h.

Erst zwanzig Jahre später fand William Huggins die vorhergesagte spektroskopische Doppler-Verschiebung im Licht von Sternen. Er zeigte, dass Sirius sich stetig von uns entfernt.

Ein weiteres Jahrhundert später wurde durch Radar-Messungen zwischen Erde und Venus die Genauigkeit der Astronomischen Einheit von 10⁻⁴ (aus der Horizontalparallaxe von Eros) verbessert auf zunächst 10⁻⁶ anhand von Entfernungsmessungen in den unteren Konjunktionen der Jahre 1959 und 1961 (z.B. beim Jet Propulsion Laboratory durch Amplitudenmodulation mit bis zu 32 Hz), dann auf 10⁻⁸ durch Doppler-Messungen auf den Trägerfrequenzen über mehrere Monate vor und nach den unteren Konjunktionen der Jahre 1964 und 1966. Die Ergebnisse wurden wie 300 Jahre zuvor als Laufzeit angegeben, da der Wert der Lichtgeschwindigkeit damals erst auf sechs Stellen bekannt war.

Für den Nachweis der Periheldrehung des Merkur reichten Doppler-Messungen der Jahre 1964 bis 1966 – mit optischen Methoden waren anderthalb Jahrhunderte nötig.

Details zum akustischen Doppler-Effekt

Wellenfronten einer gegenüber dem Medium bewegten Punktquelle demonstrieren die Abhängigkeit der Wellenlänge von der Ausbreitungsrichtung

Doppler-Effekt am Beispiel zweier sich bewegender Polizeiwagen und eines ortsfesten Mikrophons

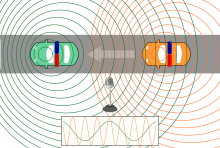
Bei der Erklärung des akustischen Doppler-Effekts ist zu unterscheiden, ob sich die Schallquelle, der Beobachter, oder beide relativ zum Medium (der ruhenden Luft) bewegen.

Beobachter in Ruhe, Signalquelle bewegt

Als Beispiel soll angenommen werden, dass das Martinshorn des Krankenwagens Schallwellen mit einer Frequenz von 1000 Hz aussendet. Dieses bedeutet, dass genau 1/1000 Sekunde nach dem ersten Wellenberg ein zweiter Wellenberg nachfolgt. Die Wellen breiten sich mit der Schallgeschwindigkeit $c\approx 340\,{\mathrm {m/s}}$ bei 20 °C aus.

Solange der Krankenwagen steht, ist die Wellenlänge $\lambda _{{\mathrm {S}}}$ des Schalls, also der Abstand der Wellenberge:

$\lambda _{\mathrm {S} }=340\,\mathrm {\frac {m}{s}} \cdot {\frac {1}{1000}}\,\mathrm {s} =0{,}34\,\mathrm {m} \,.$

Für einen Beobachter an der Straße kommen diese Wellenberge zwar je nach Entfernung etwas zeitverzögert an. Die Zeit zwischen zwei Wellenbergen ändert sich jedoch nicht. Die Grundfrequenz $f_{\mathrm {S} }$ des wahrgenommenen Tons ist für jeden Abstand von Beobachter und Krankenwagen gleich.

Die Situation ändert sich, wenn der Krankenwagen mit der Geschwindigkeit auf den Beobachter zufährt. Da sich der Wagen in der Zeit zwischen den beiden Wellenbergen weiterbewegt, verkürzt sich der Abstand zwischen ihnen etwas. Er verkürzt sich um den Weg, den der Wagen in der Zeit von 1/1000 Sekunde zurücklegt:

$\lambda _{\mathrm {B} }=\lambda _{\mathrm {S} }-{\frac {v_{\mathrm {S} }}{f_{\mathrm {S} }}}\,.$

Die Indizes ${\mathrm {S}}$ und $\mathrm {B}$ verweisen auf den Sender beziehungsweise Beobachter der Welle. Da sich beide Wellenberge mit derselben Schallgeschwindigkeit zum Beobachter bewegen, bleibt der verkürzte Abstand zwischen ihnen erhalten, und der zweite Wellenberg kommt nicht erst 1/1000 Sekunde nach dem ersten an, sondern schon ein wenig früher. Bezogen auf obiges Beispiel verkürzt sich die Wellenlänge bei einer Geschwindigkeit von $36\,{\mathrm {{\frac {km}{h}}}}=10\,{\mathrm {{\frac {m}{s}}}}$ :

Dadurch erscheint dem Beobachter die Frequenz (also die Tonhöhe) des Martinshornes höher ( $f_{{\mathrm {B}}}>f_{{\mathrm {S}}}$ ):

Quantitativ erhält man die Frequenzänderung einfach durch Einsetzen der Beziehung $\lambda \cdot f=c$ in obige Formel für $\lambda _{{\mathrm {B}}}$ . Für die vom Beobachter wahrgenommene Frequenz $f_{{\mathrm {B}}}$ ergibt sich somit:

$f_{\mathrm {B} }={\frac {f_{\mathrm {S} }}{1-{\frac {v}{c}}}}\,.$		(1)

Dabei bedeuten $f_{\mathrm {S} }$ die Frequenz der Schallquelle, die Ausbreitungsgeschwindigkeit des Schalls und die Geschwindigkeit der Schallquelle (also des Krankenwagens).

Wenn der Krankenwagen am Beobachter vorbeigefahren ist, verhält es sich sinngemäß umgekehrt: der Abstand zwischen den Wellenbergen (Wellenlänge) vergrößert sich, und der Beobachter hört einen tieferen Ton. Rechnerisch gilt obige Formel genauso, man muss nur für eine negative Geschwindigkeit einsetzen. Bezogen auf das Beispiel:

Die beschriebenen Bewegungen der Signalquelle direkt auf den Beobachter zu oder direkt von ihm weg sind Spezialfälle. Bewegt sich die Signalquelle beliebig im Raum mit der Geschwindigkeit ${\vec {v}}$ so kann die Doppler-Verschiebung für einen ruhenden Empfänger zu

$f_{\mathrm {B} }={\frac {f_{S}}{1-{\frac {{\vec {v}}\cdot {\vec {e}}_{\mathrm {SB} }}{c}}}}$

angegeben werden. ${\vec {e}}_{{\mathrm {SB}}}$ ist dabei der zeitabhängige Einheitsvektor, der die Richtung von der Signalquelle ${\mathrm {S}}$ zum Beobachter $\mathrm {B}$ beschreibt.

Beobachter bewegt, Signalquelle in Ruhe

Auch bei ruhender Schallquelle ${\mathrm {S}}$ und bewegtem Beobachter $\mathrm {B}$ tritt ein Doppler-Effekt auf, allerdings ist hier die Ursache eine andere: Wenn der Wagen ruht, ändert sich auch nichts am Abstand zwischen den Wellenbergen, die Wellenlänge bleibt also gleich. Allerdings kommen die Wellenberge scheinbar schneller hintereinander bei dem Beobachter an, wenn sich dieser auf den Krankenwagen zubewegt:

${\begin{aligned}\lambda _{\mathrm {B} }&=\lambda _{\mathrm {S} }\,,\\(c+v)\,T_{\mathrm {B} }&=c\,T_{\mathrm {S} }\end{aligned}}$

bzw.

$f_{\mathrm {B} }=f_{\mathrm {S} }\left(1+{\frac {v}{c}}\right)\,.$		(2)

Auch hier ergibt sich wieder der Fall eines sich entfernenden Beobachters durch Einsetzen einer negativen Geschwindigkeit.

Für eine beliebige Bewegung des Beobachters $\mathrm {B}$ mit dem Geschwindigkeitsvektor ${\vec {v}}$ ergibt sich bei ruhendem Sender ${\mathrm {S}}$ der Doppler-Effekt zu

$f_{\mathrm {B} }=f_{\mathrm {S} }\left(1-{\frac {{\vec {v}}\cdot {\vec {e}}_{\mathrm {SB} }}{c}}\right)$

wobei ${\vec {e}}_{{\mathrm {SB}}}$ wiederum der Einheitsvektor zur Beschreibung der Richtung von der Signalquelle ${\mathrm {S}}$ zum Beobachter $\mathrm {B}$ ist, der im allgemeinen Fall, genau wie der Geschwindigkeitsvektor ${\vec {v}}$ , zeitabhängig sein kann.

Wie man sieht, sind die Gleichungen (1) und (2) nicht identisch (nur im Grenzfall $v\ll c$ nähern sie sich einander an). Offensichtlich wird das im Extremfall: bewegt sich der Beobachter mit Schallgeschwindigkeit auf die Signalquelle zu, erreichen ihn die Wellenberge doppelt so schnell, und er hört einen Ton doppelter Frequenz. Bewegt sich hingegen die Signalquelle mit Schallgeschwindigkeit, wird der Abstand zwischen den Wellenbergen praktisch null, sie überlagern sich und es kommt zu einer extremen Verdichtung der Luft (siehe Schallmauerdurchbruch).

Beobachter und Signalquelle bewegt

Durch Kombination der Gleichungen (1) und (2) kann man eine Gleichung herleiten, welche die für den Beobachter wahrgenommene Frequenz $f_{{\mathrm {B}}}$ beschreibt, wenn der Sender und der Empfänger in Bewegung sind.

Sender und Empfänger bewegen sich aufeinander zu:

$f_{\mathrm {B} }=f_{\mathrm {S} }\cdot {\frac {1+{\frac {v_{\mathrm {B} }}{c}}}{1-{\frac {v_{\mathrm {S} }}{c}}}}=f_{\mathrm {S} }\cdot {\frac {c+v_{\mathrm {B} }}{c-v_{\mathrm {S} }}}\,.$

Sender und Empfänger bewegen sich voneinander weg:

$f_{\mathrm {B} }=f_{\mathrm {S} }\cdot {\frac {1-{\frac {v_{\mathrm {B} }}{c}}}{1+{\frac {v_{\mathrm {S} }}{c}}}}=f_{\mathrm {S} }\cdot {\frac {c-v_{\mathrm {B} }}{c+v_{\mathrm {S} }}}\,.$

Dabei ist $v_{\mathrm {B} }$ die Geschwindigkeit des Beobachters und $v_{\mathrm {S} }$ die Geschwindigkeit des Senders der Schallwellen relativ zum Medium.

Frequenzverschiebung bei Streuung an einem bewegten Objekt

Ebenfalls aus den oberen Gleichungen lässt sich die wahrgenommene Frequenz ableiten wenn die Welle eines ruhenden Senders ${\mathrm {S}}$ an einem mit der Geschwindigkeit ${\vec {v}}$ bewegten Objekt $\mathrm{O}$ gestreut wird und von einem ebenfalls ruhenden Beobachter $\mathrm {B}$ wahrgenommen wird:

$f_{\mathrm {B} }=f_{\mathrm {S} }{\frac {1-{\frac {{\vec {v}}\cdot {{\vec {e}}_{\mathrm {SO} }}}{c}}}{1-{\frac {{\vec {v}}\cdot {\vec {e}}_{\mathrm {OB} }}{c}}}}\,.$

${\vec {e}}_{\mathrm {SO} }$ und ${\vec {e}}_{\mathrm {OB} }$ sind dabei jeweils die Einheitsvektoren vom stationären Sender zum bewegten Objekt und vom bewegten Objekt zum stationären Beobachter.

Anwendung findet diese Gleichung häufig in der akustischen oder optischen Messtechnik zur Messung von Bewegungen, z.B. Laser-Doppler-Anemometrie. Speziell in der Optik kann für $\left|{\vec {v}}\right|\ll c$ die Winkelabhängigkeit der gestreuten Frequenz zu

$f_{\mathrm {B} }\approx f_{\mathrm {S} }\left(1+{\frac {\vec {v}}{c}}\cdot ({\vec {e}}_{\mathrm {OB} }-{\vec {e}}_{\mathrm {SO} })\right)$

aus Beleuchtungsrichtung ${\vec {e}}_{\mathrm {SO} }$ und Beobachtungsrichtung ${\vec {e}}_{\mathrm {OB} }$ in sehr guter Näherung bestimmt werden.

Allgemeines Doppler-Gesetz für Schallquellen

Allgemein lässt sich der Frequenzunterschied schreiben als:

$f_{\mathrm {B} }=f_{\mathrm {S} }\left({\frac {c\pm v_{\mathrm {B} }}{c\mp v_{\mathrm {S} }}}\right)\,.$

Dabei ist $v_{\mathrm {B} }$ die Geschwindigkeit des Beobachters und $v_{\mathrm {S} }$ die der Schallquelle, jeweils relativ zum Medium (z. B. der Luft). Das obere Operationszeichen gilt jeweils für Annäherung (Bewegung in Richtung des Senders bzw. Empfängers). D. h. beide Geschwindigkeiten werden positiv in Richtung des Beobachters bzw. Senders gemessen. Mit $v_{\mathrm {B} }=0$ oder $v_{\mathrm {S} }=0$ ergeben sich die oben genannten Spezialfälle. Für $v_{\mathrm {S} }=-v_{\mathrm {B} }$ verschwindet der Effekt (es gibt also keine Tonhöhenänderung). Das tritt ein, wenn sich Sender und Empfänger in dieselbe Richtung mit derselben Geschwindigkeit relativ zum Medium bewegen; meist bewegt sich in solchen Fällen das Medium selbst, während Sender und Empfänger ruhen (Wind). Deswegen kommt es unabhängig von der Windstärke zu keinem Doppler-Effekt.

Die Formeln wurden unter der Annahme abgeleitet, dass sich Quelle und Beobachter direkt aufeinander zubewegen. In realen Fällen fährt z. B. der Krankenwagen in einem bestimmten Mindestabstand am Beobachter vorbei. Daher ändert sich der Abstand zwischen Quelle und Beobachter nicht gleichmäßig, und deswegen ist – besonders unmittelbar vor und nach dem Vorbeifahren – ein kontinuierlicher Übergang der Tonhöhe von höher zu tiefer zu hören.

Doppler-Effekt ohne Medium

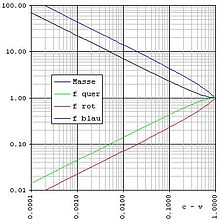
Relativistischer Doppler-Effekt und Geschwindigkeit

Elektromagnetische Wellen breiten sich auch im Vakuum, also ohne Medium aus. Wenn sich der Sender der Wellen relativ zum Empfänger bewegt, tritt auch in diesem Fall eine Verschiebung der Frequenz auf. Dieser Relativistische Doppler-Effekt ist darauf zurückzuführen, dass die Wellen sich mit endlicher Geschwindigkeit, nämlich der Lichtgeschwindigkeit ausbreiten. Man kann ihn als geometrischen Effekt der Raumzeit auffassen.

Longitudinaler Doppler-Effekt

Im Vakuum (Optischer Doppler-Effekt) hängt die beobachtete Frequenzänderung nur von der relativen Geschwindigkeit von Quelle und Beobachter ab; ob sich dabei die Quelle, der Beobachter oder beide bewegen, hat keinen Einfluss auf die Höhe der Frequenzänderung.

Aufgrund des Relativitätsprinzips darf sich jeder Beobachter als ruhend betrachten. Allerdings muss er dann bei der Berechnung des Doppler-Effekts zusätzlich zu obigen Betrachtungen auch noch die Zeitdilatation der relativ zum Beobachter bewegten Quelle berücksichtigen. Somit erhält man für den relativistischen Doppler-Effekt:

$f_{\mathrm {B} }={\frac {f_{\mathrm {S} }{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}{1-{\frac {v}{c}}}}=f_{\mathrm {S} }{\sqrt {\frac {c+v}{c-v}}}$

v > 0 bei Verringerung des Abstandes zwischen Quelle und Beobachter.

Transversaler Doppler-Effekt

Bewegt sich ein Objekt zu einem gewissen Zeitpunkt quer zum Beobachter, so kann man die Änderung des Abstandes zu diesem Zeitpunkt vernachlässigen; dementsprechend würde man hier auch keinen Doppler-Effekt erwarten. Jedoch besagt die Relativitätstheorie, dass jedes Objekt aufgrund seiner Bewegung einer Zeitdilatation unterliegt, aufgrund der die Frequenz ebenfalls verringert wird. Diesen Effekt bezeichnet man als transversalen Doppler-Effekt. Die Formel hierfür lautet

$f_{\mathrm {B} }={\frac {f_{\mathrm {S} }}{\gamma }}=f_{\mathrm {S} }{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}\approx f_{\mathrm {S} }\left(1-{\frac {v^{2}}{2c^{2}}}\right)\,,$

wobei hier die Vakuum-Lichtgeschwindigkeit und die Geschwindigkeit der Signalquelle bezeichnet.

Der transversale Doppler-Effekt kann bei nicht-relativistischen Geschwindigkeiten (also Geschwindigkeiten weit unter der Lichtgeschwindigkeit) allerdings vernachlässigt werden.

Doppler-Effekt bei beliebigem Winkel

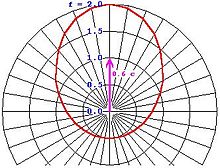
Relativistischer Doppler-Effekt und Richtung

Der Doppler-Effekt lässt sich ganz allgemein abhängig vom Winkel der Bewegungsrichtung zur Achse Quelle-Empfänger angeben. Die Frequenzänderung für beliebige Winkel $\alpha$ ergibt sich zu

$f_{\mathrm {B} }=f_{\mathrm {S} }{\frac {\sqrt {1-{\frac {v^{2}}{c^{2}}}}}{1-{\frac {v}{c}}\cos {\alpha }}}\,.$

Wenn man für den Winkel $\alpha$ nun 0° (Quelle bewegt sich direkt auf Empfänger zu), 90° (Quelle bewegt sich seitwärts) oder 180° (Quelle bewegt sich direkt vom Empfänger weg) einsetzt, dann erhält man die oben stehenden Gleichungen für longitudinalen und transversalen Doppler-Effekt. Man erkennt außerdem, dass der Winkel, unter dem der Doppler-Effekt verschwindet, von der Relativgeschwindigkeit abhängt, anders als beim Doppler-Effekt für Schall, wo er immer 90° beträgt.

Doppler-Effekt und astronomische Rotverschiebung

Auch wenn die zu beobachtenden Auswirkungen von Doppler-Effekt und astronomischer Rotverschiebung identisch sind (Verminderung der beobachteten Frequenz der elektromagnetischen Strahlung eines Sterns oder einer Galaxie), so dürfen beide trotzdem nicht verwechselt werden, da sie gänzlich andere Ursachen haben. Der relativistische Doppler-Effekt ist nur dann Hauptursache für die Frequenzänderung, wenn sich Sender und Empfänger wie oben beschrieben durch die Raumzeit bewegen und ihr Abstand so gering ist, dass die Ausdehnung des zwischen ihnen liegenden Raumes im Verhältnis gering ist. Ab einer bestimmten Entfernung überwiegt bei weitem jener Anteil, der durch die Ausdehnung der Raumzeit selbst hervorgerufen wird, so dass der Anteil des hier diskutierten Doppler-Effekts gänzlich vernachlässigt werden kann.

Anwendungen

Radialgeschwindigkeiten sind durch den Doppler-Effekt messbar, wenn der Empfänger die Frequenz des Senders genügend genau kennt, insbesondere bei Echos von akustischen und elektromagnetischen Signalen.

Physik und Astrophysik

Scharfe Spektrallinien erlauben eine entsprechend hohe Auflösung der Doppler-Verschiebung. Berühmt ist der Nachweis der Doppler-Verschiebung im Gravitationsfeld (Pound-Rebka-Experiment). Beispiele in der Astrophysik sind die Rotationskurven von Galaxien, spektroskopische Doppelsterne, die Helioseismologie und der Nachweis von Exoplaneten.

In der Quantenoptik wird die Dopplerverschiebung bei der Laserkühlung von Atomgasen genutzt, um Temperaturen nahe dem absoluten Nullpunkt zu erreichen.

Bei der Mößbauer-Spektroskopie wird der Doppler-Effekt einer bewegten Gammastrahlungsquelle verwendet, um die Energie der Photonen dieser Quelle minimal zu verändern. Hierdurch können diese Photonen in Wechselwirkung mit den Kernhyperfeinniveaus eines entsprechenden Absorbers treten.

Radartechnik

Wetterradar

Doppler-Radar MIM-23 Hawk

Beim Doppler-Radar berechnet man die Annäherungsgeschwindigkeit eines Objekts aus der gemessenen Frequenzänderung zwischen gesendetem und reflektiertem Signal. Die Besonderheit bei einem aktiven Radargerät ist jedoch, dass der Doppler-Effekt zweimal auftreten kann, auf dem Hin- und auf dem Rückweg. Ein Radarwarngerät, das die Signale des Hinwegs empfängt, misst eine Frequenz, die in Abhängigkeit von der Relativgeschwindigkeit variiert. Diese registrierte Frequenz wird von ihm reflektiert. Das Radargerät registriert die bereits Doppler-verschobenen Frequenzen wiederum in Abhängigkeit von der dann bestehenden Relativgeschwindigkeit. Im Fall eines unbeschleunigten Radargeräts tritt eine exakt zweifache Doppler-Verschiebung auf.

In der Meteorologie wird das Doppler-Radar zur Bestimmung von Rotationsbewegungen in Superzellen (Tornados) benutzt.
Das Militär und die Flugüberwachung nutzen den Doppler-Effekt unter anderem beim Passiv-Radar und bei der Festzielunterdrückung.
Auch zur Geschwindigkeitsermittlung bei sog. Radarfallen im Straßenverkehr wird ein Doppler-Radar benutzt.
Ein Synthetic Aperture Radar basiert maßgeblich auf der Zuordnung der Signale durch den Verlauf der Änderung ihrer Doppler-Verschiebung.

Medizinische Diagnostik

In der Medizin wird der akustische Doppler-Effekt bei Ultraschalluntersuchungen ausgenutzt, um die Blutstromgeschwindigkeit darzustellen und zu messen. Dabei hat er sich als außerordentlich hilfreich erwiesen. Es gibt dabei einen:

Farb-Doppler:
- Rot: Fluss auf die Schallsonde zu
- Blau: Fluss von der Schallsonde weg
pW-Doppler: gepulster Doppler (beispielsweise für Gefäßuntersuchungen)
cW-Doppler: continuous wave Doppler (beispielsweise für Herzklappenmessungen)

Laser-Doppler

Für die berührungslose Messung der Geschwindigkeitsverteilung von Fluiden (Flüssigkeiten und Gase) wird die Laser-Doppler-Anemometrie (LDA) angewandt. Sie beruht auf dem optischen Doppler-Effekt an streuenden Partikeln in der Strömung. In gleicher Weise dient ein Vibrometer der Messung der Schnelle vibrierender Oberflächen.

Sonstige Anwendungen

Für Wasserwellen (Schwerewellen), deren Trägermedium einer konstanten Strömungsgeschwindigkeit unterliegt.
Das mittlerweile abgeschaltete Satellitennavigations-System Transit nutzte den Doppler-Effekt zur Positionsbestimmung. Aktiv eingesetzt wird er bei Argos, einem satellitengestützten System zur Positionsbestimmung. Bei modernen GNSS-Satelliten ist der Doppler-Effekt zunächst störend. Er zwingt die Empfänger, einen größeren Frequenzbereich abzusuchen. Andererseits lassen sich aus der Frequenzverschiebung Zusatzinformationen gewinnen und so die Grobpositionierung beschleunigen. Das Verfahren heißt Doppler-Aiding.

Beispiel

Abhängigkeit der Frequenz einer Signalquelle von der Entfernung zu einem ruhenden Beobachter für verschiedene Minimalabstände.

Ein ruhender Beobachter hört eine Schallquelle, die sich genau auf ihn zubewegt, mit der Frequenz $f'_{\mathrm {zu} }(v/c)$ , siehe Gleichung (1), wenn sie sich von ihm entfernt, mit der Frequenz $f'_{\mathrm {weg} }(v/c)$ , siehe Gleichung (2). Bei Schallquellen spielt der relativistische transversale Doppler-Effekt keine Rolle. Je weiter der Beobachter von der linearen Flugbahn entfernt ist, desto langsamer ändert sich die radiale Geschwindigkeitskomponente bei Annäherung. 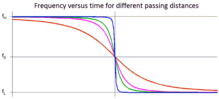Die Schnelligkeit der Frequenzänderung hängt ab von der kürzesten Entfernung zwischen Beobachter und Signalquelle. Das Diagramm rechts zeigt die Frequenzabhängigkeit relativ zu einem im Ursprung ruhenden Beobachter. Die rote Linie entspricht der Frequenz, die er hört, wenn ihn die Signalquelle in großem Abstand passiert, blau der bei geringem Abstand. Maximal- und Minimal-Frequenzen liegen nicht symmetrisch zur Eigenfrequenz, da die Geschwindigkeit nicht sehr viel kleiner ist als die Schallgeschwindigkeit . Es gelten die Beziehungen (1) und (2).

Sind die Koordinaten der bewegten Signalquelle bekannt, kann man aus dem Frequenzverlauf den eigenen Standort ableiten.

Basierend auf einem Artikel in:

Wikipedia.de