Doppelspaltexperiment
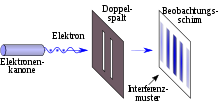
Beim Doppelspaltexperiment lässt man kohärente Wellen, zum Beispiel Licht- oder Materiewellen, durch zwei schmale, parallele Spalte treten. Auf einem Beobachtungsschirm in einer Distanz zur Blende, die sehr viel größer ist als der Abstand a der beiden Spalte, zeigt sich ein Interferenzmuster. Dieses Muster entsteht durch Beugung der Wellenausbreitung am Doppelspalt. Bei monochromatischem Licht (z.B. von einem Laser) besteht dieses Muster auf dem Schirm aus hellen Streifen (Maxima) und dunklen Streifen (Minima). Das Interferenzmuster entsteht nur, wenn die Wellenlänge λ kleiner als der Abstand a der beiden Spalte ist.
Das Experiment gehört zu den Schlüsselexperimenten der Physik. Es wurde erstmals 1802 von Thomas Young mit Licht durchgeführt und führte zur Ablehnung der damals noch vorherrschenden Korpuskeltheorie des Lichts zugunsten der Wellentheorie. Erst Albert Einsteins Arbeiten zum Photoelektrischen Effekt deckten 1905 auch den Teilchencharakter des Lichts auf. In der Quantenphysik dient das Doppelspaltexperiment häufig dazu, den Welle-Teilchen-Dualismus zu demonstrieren. Es kann nicht nur mit Licht, sondern auch mit Teilchen (Elektronen, Neutronen, Atomen, Molekülen wie z.B. Fullerenen) durchgeführt werden. Die dabei beobachteten Interferenzmuster zeigen, dass auch die klassisch nur als Teilchen angesehenen Objekte Welleneigenschaften haben. Bei diesen Materiewellen tritt die De-Broglie-Wellenlänge an die Stelle der Wellenlänge des Lichts.
Geschichte

1802 führte Thomas Young das Experiment erstmals durch, um die Wellennatur des Lichtes zu beweisen. Dabei verwendete Young noch nicht den klassischen Doppelspalt, sondern Pappkarten, mit denen er einen Lichtstrahl teilte. Young erwähnt in seinem Werk frühere Experimente zur Natur des Lichts von Francesco Maria Grimaldi, welcher schon 1665 den Begriff der Diffraktion einführte.
1927 zeigten Clinton Davisson und Lester Germer die Welleneigenschaften von Elektronen anhand der Beugung eines Elektronenstrahls an einem Nickel-Kristall. Der Kristall wirkt dabei als Reflexionsgitter. Statt zweier Spalte sind hier sehr viele Streuzentren im Spiel.
Das Doppelspaltexperiment mit Elektronen wurde 1961 durch Claus Jönsson durchgeführt. Mit ganzen Atomen gelang es 1990 Jürgen Mlynek und Olivier Carnal, mit großen Molekülen wie z.B. C60 (Buckyballs) im Jahr 2003 Nairz et al.
Experimentelle Beobachtung

- Die beiden interferierenden Wellen müssen eine feste Phasenbeziehung zueinander haben, damit Interferenzstreifen beobachtet werden können. Ausreichende räumliche Kohärenz ist gegeben, wenn die Breite der Quelle (bei Young ein Eintrittsspalt) aus Sicht des Doppelspaltes nicht aufgelöst werden kann (siehe Rayleigh-Kriterium). Die Anforderung an die zeitliche Kohärenz hängt davon ab, wie viele Streifen man neben dem zentralen Streifen erkennen will.
- Eine Ergänzung der Apparatur, die ermittelt, durch welchen der beiden Spalte ein Teilchen den Detektor erreicht hat („Welcher-Weg“-Information), bewirkt unvermeidlich, dass die Interferenzstreifen verschwinden. Dies gilt auch dann, wenn kein makroskopisches Messgerät anzeigt, welcher Spalt genommen wurde. Es reicht die physikalische Möglichkeit dazu. Umgekehrt zeigen Aufbauten, bei denen es unmöglich ist, herauszufinden, welcher Spalt genommen wurde, immer ein Interferenzmuster. (Bei Photonen kann die Weginformation einfach durch Polarisationsfilter realisiert sein. Werden die beiden Spalte jeweils mit Filtern mit gegeneinander orthogonalen Polarisationsebene kombiniert, so entscheidet die Polarisation des Photons darüber, welchen Weg das Photon nimmt. In diesem Fall tritt keine Interferenz am Schirm auf.)
- Die beiden vorhergehenden Aussagen gelten selbst dann, wenn die Entscheidung, ob die Information über den Weg ermittelt wird, erst fällt, nachdem ein Teilchen die Spalte passiert hat. Die Entscheidung, den Weg nicht zu ermitteln, führt dazu, dass Interferenzmuster im Detektor beobachtet werden. Das kann man so deuten, dass die Information über den genommenen Weg nachträglich gelöscht wird. Daher wird ein solcher Aufbau Quantenradierer genannt.
- Das Interferenzmuster hängt nicht von der Anzahl oder Gleichzeitigkeit der beteiligten Photonen ab. Bei niedrigerer Intensität baut sich das Interferenzmuster lediglich langsamer beim Detektor auf, bleibt aber in der Gestalt gleich. Das passiert selbst dann, wenn sich zu jedem Zeitpunkt maximal ein Teilchen zwischen Quelle und Detektor befindet. Daher muss auch die Verteilung der Wahrscheinlichkeit des Ankommens an den Positionen auf dem Detektor bei jedem einzelnen Durchflug entstehen. Dieses Phänomen lässt sich als Interferenz der Teilchen mit sich selbst interpretieren.
Berechnung des Interferenzmusters

Der folgende Abschnitt geht von einem senkrechten Einfall einer ebenen Welle der
Wellenlänge
auf einen Doppelspalt mit Spaltbreite
und Spaltmittenabstand
aus. In der Spaltebene sind die Phasen noch im Gleichtakt, Phasenunterschiede,
die den Interferenzeffekt ausmachen, ergeben sich erst durch die Abstände
von Punkten in den Spaltöffnungen zum Beobachtungspunkt (rote Linien). Der
Abstand
des Schirms soll groß sein,
,
Fernfeldnäherung.
Orte der Minima und Maxima durch Interferenz der beiden Spalte
Ein Minimum der Intensität findet man für solche Orte, wo der Gangunterschied
von den Spaltmitten aus ein ungerades Vielfaches der halben Wellenlänge beträgt,
also
.
Dann sind die beiden Teilwellen gegenphasig und löschen sich aus. Das gilt auch
für den Fall, dass die Breite der Spaltöffnungen nicht klein gegenüber der
Wellenlänge ist. Dann variiert zwar
merklich mit der Lage des Punktes innerhalb der Spaltbreite, aber zu jedem Punkt
in dem einen Spalt gibt es im Abstand
einen Punkt im anderen Spalt, von dem aus die Welle gegenphasig ankommt.
Maxima befinden sich etwa mittig zwischen den Minimumstellen, wo mit
konstruktive Interferenz gegeben ist. Für höhere Beugungsordnungen
nehmen die Maximalintensitäten ab, denn die konstruktive Interferenz gilt zwar
paarweise für Punkte in beiden Spalten, aber nicht für die Variation der
Punktposition innerhalb des Spaltes (s.u.).
Für den Zusammenhang zwischen dem Gangunterschied
und der Position
auf dem Schirm liest man aus der Zeichnung ab:
also für kleine Winkel ungefähr
Damit beträgt die Periode
des Streifenmusters ,
wenn der Schirmabstand groß gegenüber dem Spaltabstand ist.
Das Interferenzmuster
Allerdings hat bereits jeder der beiden Einzelspalte ein
Beugungsmuster, da für bestimmte Winkel
sich die obere und die untere Hälfte des Einzelspalts der Breite
gerade aufheben. Die Intensität des Doppelspaltes ist daher das Produkt zweier
Intensitäten: der Beugung am Einzelspalt der Breite
und der von zwei punktförmigen Quellen im Abstand
:
wobei
der Phasenunterschied der Wellen vom oberen bzw. unterem Rand je eines Spaltes
ist, und
der Phasenunterschied zwischen den beiden Teilwellen aus beiden Spalten.
Dabei ist
der Beobachtungswinkel,
die Spaltbreite,
der Spaltabstand,
die Wellenzahl.
Einfluss von Spaltgeometrie und Wellenlänge
Setzt man die Ausdrücke für
und
in die Gleichung des Interferenzmusters ein, so werden die Einflüsse von
Spaltgeometrie und Wellenlänge des einfallenden Lichtes auf das Aussehen des
Interferenzmusters deutlich:
mit .
- Eine Änderung der Spaltbreite
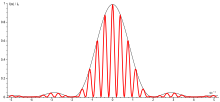
führt zu einer Änderung der Lage der Extrema des Einfachspaltes, dessen Intensitätsverteilung (im Bild blau) die Hüllkurve der Intensitätsverteilung des Doppelspalts bildet (im Bild rot)
- → Je breiter der Spalt, desto enger wird die Hüllkurve
- Eine Änderung des Spaltabstandes
führt zu einer Änderung der Lage der Extrema des Doppelspalts innerhalb der konstant bleibenden Hüllkurve
- → Je größer der Spaltabstand, desto enger liegen die Extrema des Doppelspalts beieinander
- Eine Änderung der Wellenlänge
wirkt sich sowohl auf die Hüllkurve als auch auf die Intensitätsverteilung des Doppelspalts aus
- → Je größer die Wellenlänge, desto breiter werden Hüllkurve und die Interferenzabstände des Doppelspalts
Berechnung mit Fourier-Optik
Das Interferogramm einer Spaltkonstellation lässt sich auch mit Hilfe der Fourier-Optik berechnen. Dabei wird ausgenutzt, dass im Falle der Fraunhofer-Beugung das Beugungsmuster der Fouriertransformierten der Autokorrelation der Blendenfunktion entspricht. Der Vorteil dieses Ansatzes ist, dass sich auch das Beugungsbild komplizierterer Mehrfachspalte und Gitter schnell berechnen lässt. Wesentlich ist dabei die Ausnutzung des Faltungstheorems.
Das Koordinatensystem wird so gelegt, dass die zwei Einzelspalte einen
Abstand
haben und symmetrisch zum Schnitt der Koordinatenachsen liegen. Die
Blendenfunktion der zwei identischen Spalte mit Breite
im Ortsraum lautet
wobei
den Faltungsoperator
und
die Rechteckfunktion
bezeichnet.
Die Fouriertransformierte der gegebenen Blendenfunktion ist nach dem Faltungstheorem das Produkt aus der Fouriertransformierten der Rechteckfunktion und der Fouriertransformierten der zwei Delta-Distributionen.
Daraus folgt für die Intensität
am Schirm ein Cosinus mit einer Sinc-Funktion
als Einhüllende. Die Funktion weist die charakteristischen
Nebenmaxima eines
-fach-Spaltes
auf (siehe auch Optisches
Gitter).
Mit
als Intensitätskonstante.
Für
folgt die oben bereits gezeigte Beziehung für
.
Literatur
- John Gribbin: Auf der Suche nach Schrödingers Katze. Quantenphysik und Wirklichkeit. 5. Auflage. Piper, 2004, ISBN 3-492-24030-5.
- Claus Jönsson: Interferenz von Elektronen am Doppelspalt. In: Zeitschrift für Physik, Nr. 161, 1961, S. 454–474.
- David Halliday, Robert Resnick, Jearl Walker: Physik. 2. Auflage. Wiley-VCH, 2003, ISBN 3-527-40366-3.
- Wolfgang Demtröder: Experimentalphysik. Bd.2 : Elektrizität und Optik. 3. Auflage. Springer, Berlin, 2004, ISBN 3-540-20210-2.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 12.06. 2022