Kleinwinkelnäherung
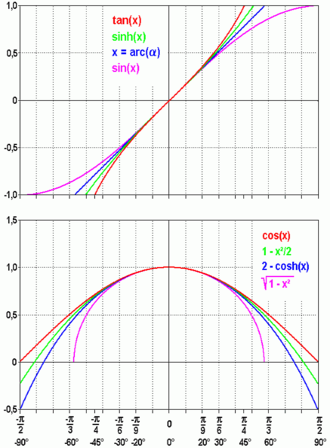
Unter der Kleinwinkelnäherung wird die mathematische Näherung verstanden, bei
der angenommen wird, der Winkel
sei so hinreichend klein, dass man seinen Sinus oder Tangens
durch den Winkel selbst (in Radiant)
und den Kosinus
durch
ersetzen kann.
Herleitung
Grundlage dieses Ansatzes ist die jeweilige Maclaurinsche Reihe der Winkelfunktion (siehe auch Taylor-Reihe):
Für
kann man die Summanden mit höherer Potenz von
vernachlässigen gegenüber den vorhergehenden Gliedern, so dass sich die
Näherungen ergeben:
Zur Beurteilung, bis zu welchem Winkel die Näherungen im Rahmen akzeptierter Fehlergrenzen zulässig sind, werden einige relative Abweichungen angegeben:
| Relative Abweichung bei | |||
|---|---|---|---|
| Näherung | |||
Anwendungen
Wichtig ist die Kleinwinkelnäherung besonders in der Physik, wo sich viele Probleme mit Hilfe der Kleinwinkelnäherung analytisch exakt lösen lassen, die ansonsten unter Einbeziehung der Winkelfunktionen zu komplizierten elliptischen Integralen führen würden. Anwendungsbeispiele der Kleinwinkelnäherung sind das mathematische Pendel, die Auswertung der Beugung am Spalt, die paraxiale Optik sowie die Annäherung von Parabel und Kreisbogen bei der Behandlung bei Linsen und Hohlspiegeln in der Nähe der optischen Achse.
Moderate Winkeländerungen > 7°
In der technischen Mechanik ist ebenfalls die Berücksichtigung moderater Winkeländerungen üblich. Um zu vermeiden, dass der Kosinus bei der Kleinwinkelapproximierung komplett herausfällt, wird zusätzlich das zweite Glied der Taylorreihenentwicklung berücksichtigt, sodass gilt:
.
Ein Anwendungsbeispiel ist die Theorie leicht gekrümmter Schalentragwerke: Da die Krümmung das Tragverhalten maßgeblich beeinflusst, muss diese berücksichtigt werden; gleichzeitig soll die Approximation den Berechnungsaufwand verringern.
Durch die genauere Näherung ergeben sich nun folgende Eigenschaften:
| Relative Abweichung bei | |||
|---|---|---|---|
| Näherung | |||


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 03.03. 2022