Laue-Bedingung
Die Laue-Bedingung, nach Max von Laue, ist eine zur Bragg-Bedingung äquivalente Beschreibung von Beugungseffekten an Kristallen. Sie gibt Auskunft über das Auftreten von Beugungsreflexen bei elastischer Streuung von Röntgenstrahlung, Elektronen oder Neutronen an Kristallen.
Zur Erklärung der Röntgenbeugung gibt es zwei äquivalente Ansätze. In beiden werden Kristalle als starre periodische Strukturen von mikroskopischen Objekten angesehen. Bei der Bragg-Theorie werden die Atome im Kristall in parallelen Gitterebenen mit konstantem Abstand angeordnet. An diesen Ebenen kommt es zur spiegelnden Reflexion der Strahlung. Bei der Von-Laue-Theorie geht man von anderen Annahmen aus:
- Beschreibe den Kristall als Bravaisgitter
- An den Gitterplätzen sitzen identische mikroskopische Objekte, die die einfallende Strahlung streuen
- Reflexe nur in Richtungen, für die von den Gitterpunkten gestreute Strahlung konstruktiv interferiert
Die Laue-Bedingung lautet: Man erhält genau dann konstruktive Interferenz, wenn die Änderung des Wellenvektors beim Streuprozess einem reziproken Gittervektor entspricht.
Die Laue-Bedingung geht vom reinen Kristallgitter (am Gitterpunkt ein punktförmiges Streuzentrum) aus und gibt an, in welcher Richtung Beugungsreflexe beobachtet werden können. Die relative Intensität der Reflexe hängt vom Aufbau der Basis, dem Streuvermögen der Basisatome und von der thermischen Bewegung der Atome ab. Dies wird durch den Strukturfaktor beschrieben.
Herleitung der Laue-Bedingung
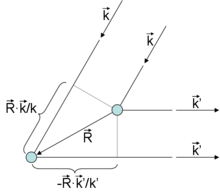
Der Abstand zweier Streuzentren (Gitterpunkte) ist ein Gittervektor .
Der Wellenvektor der einfallenden Strahlung sei
,
der der gestreuten sei
.
Damit ergibt sich folgender Gangunterschied
(Wegdifferenz):
Für konstruktive Interferenz
muss der Gangunterschied ein ganzzahliges Vielfaches der Wellenlänge
sein:
Gleichsetzen liefert:
Geht man von elastischer Streuung aus, ist die Wellenzahl des einfallenden
und des reflektierten Strahls gleich: .
Für alle Gittervektoren
muss gelten:
bzw. äquivalent
Dies entspricht genau der Bestimmungsgleichung für reziproke
Gittervektoren :
Die Laue-Bedingung lautet somit: Man erhält genau dann konstruktive Interferenz, wenn die Änderung des Wellenvektors beim Streuprozess einem reziproken Gittervektor entspricht.
bzw.
Laue-Gleichungen und Laue-Indizes
Reziproke Gittervektoren lassen sich als Linearkombination der primitiven
Gittervektoren des reziproken Gitters
ausdrücken, dabei sind
die Laue-Indizes (s.u.):
Ebenso lassen sich die Gittervektoren als Linearkombination der primitiven
Gittervektoren
darstellen mit
:
Das Skalarprodukt
aus primitiven Gittervektoren des Ortsraums
und des reziproken Raums
ist:
wobei
das Kronecker-Symbol
ist.
Bildet man das Skalarprodukt der obigen Laue-Bedingung
mit den primitiven Ortsvektoren, erhält man die drei Laue-Gleichungen:
Die drei ganzen Zahlen
(normalerweise
,
hier aber Verwechslungsgefahr mit Wellenzahl
,
deswegen
)
heißen dabei die Laue-Indizes. Die drei Gleichungen definieren jeweils
einen Kegel (für h=0 zu einer Ebene entartet). Damit alle Bedingungen
erfüllt sind, müssen sich drei Kegelflächen in dieser Raumrichtung
zusammentreffen. Dadurch werden die punktförmigen Interferenzmuster der
Röntgenbeugung an Kristallgittern erklärt und indiziert.
Zeitgleich mit Laue
stellten W.H. Bragg
und W.L. Bragg
die Bragg-Bedingung
für die Reflexion an parallelen Flächen im Abstand d auf. Auch wenn die
Herangehensweisen von Laue (Beugung
in alle Raumrichtungen) und Bragg (Reflexion)
verschieden sind, sind die beiden Effekte äquivalent: Hat die Schar von
Netzebenen, die in der Bragg-Bedingung gerade den Abstand d haben, im
Kristall die Millerschen
Indizes (hkl), so hat der Interferenzpunkt die Laue-Indizes nh nk
nl, die Laue-Indizes sind also gerade das n-fache der Miller-Indizes.
Aufgrund des Zusammenhangs mit der Bragg-Reflexion werden die Laue-Indizes
gelegentlich auch als Bragg-Indizes bezeichnet.
Alternative Formulierung der Laue-Bedingung
Man kann die Laue-Bedingung noch in alternativer Form schreiben. Man
quadriere die Laue-Bedingung
und benutze
(elastische Beugung):
also
Teile durch :
Für ein gegebenes
ist dies eine Ebenengleichung
in der Hesse-Normalenform.
Die Projektion von
auf die Richtung von
ist konstant
.
Ein Wellenvektor der einfallenden Strahlung
erfüllt die Laue-Bedingung, wenn seine Spitze in einer Bragg-Ebene liegt.
Eine Bragg-Ebene ist die mittelsenkrechte Ebene auf der Verbindungslinie
zwischen dem Ursprung im reziproken Raum und einem Punkt
.
Diese Ebenengleichung entspricht für benachbarte Punkte im reziproken Raum der
Konstruktionsvorschrift der Wigner-Seitz-Zelle
des reziproken Gitters (erste Brillouin-Zone).
Daraus folgt die Alternative Formulierung der Laue-Bedingung: Man erhält genau dann konstruktive Interferenz, wenn die Spitze des einfallenden Wellenvektors auf dem Rand einer Brillouin-Zone liegt.
Äquivalenz von Laue- und Bragg-Bedingung
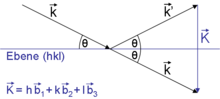
Geht man von
und
aus, so ergibt sich:
Der Winkel zwischen
und
sei
:
mit
und Kosinussatz
Radizieren liefert:
Das Skalarprodukt zwischen einem reziproken Gittervektor und einem Gittervektor ergibt:
somit
Für ein gegebenes
ist dies eine Ebenengleichung für eine Gitterebene, wobei
senkrecht auf dieser Ebene steht. Schreibt sich
als folgende Linearkombination
,
so steht der Vektor senkrecht auf der Gitterebene
.
Der Gitterebenenabstand
ist
.
Mit
und
erhält man aus
die Bragg-Bedingung (n entspricht der Ordnung des Beugungsreflexes):
Beugungsreflex
- nach Laue: Änderung des Wellenvektors um reziproken Gittervektor
- nach Bragg: Reflexion an Netzebenenschar des Kristallgitters, die
senkrecht zu
steht und deren Abstand
beträgt.
Literatur
- Martin J. Buerger: Kristallographie. 1. Auflage. Walter de Gruyter, Berlin 1977, ISBN 3-11-004286-X.
- Neil W. Ashcroft, N. David Mermin: Festkörperphysik. 2. Auflage. Oldenbourg, München 2005, ISBN 3-486-57720-4.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 29.06. 2021