Brillouin-Zone

Erste Brillouin-Zone eines kubisch-flächenzentrierten Gitters (das reziproke Gitter ist also kubisch-raumzentriert)

Die Brillouin-Zonen (nach Léon Brillouin) beschreiben in der Festkörperphysik symmetrische Polyeder im reziproken Gitter. Die erste Brillouin-Zone ist die primitive Wigner-Seitz-Zelle des reziproken Gitters eines Kristalls, also ein (i.A. unregelmäßiges) Polyeder im reziproken Raum. Nach der ersten Brillouin-Zone wiederholt sich die gesamte Struktur periodisch, d.h., es reicht, alle Prozesse in der ersten Brillouin-Zone zu beschreiben.

Konstruktion

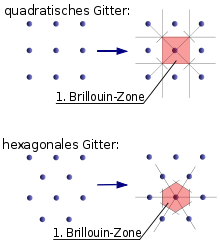
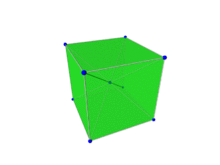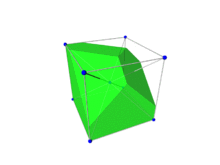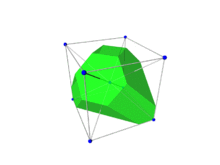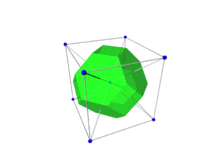
1. Brillouin-Zone im zweidimensionalen quadratischen und hexagonalen Gitter

Animierte Konstruktion der 1. Brillouin-Zone eines kubisch raumzentrierten Gitters (krz-Gitter)

Für die Konstruktion analog zu der Wigner-Seitz-Zelle wählt man einen Gitterpunkt des reziproken Gitters und halbiert alle Verbindungsstrecken zu sämtlichen anderen Punkten durch Normalebenen, d.h. durch Ebenen, auf denen die Verbindungsstrecken jeweils senkrecht stehen. Indem man die Mittelsenkrechte (bzw. -ebene in 3D) zu allen Punkten einzeichnet, erhält man rund um den Gitterpunkt eine Fläche (bzw. Volumen in 3D). Das Polyeder, das durch die Normalebenen begrenzt wird, ist die Brillouin-Zone.

Innerhalb der ersten Brillouin-Zone (1. BZ) werden einige wichtige hochsymmetrische Punkte des fcc-Gitters benannt. Mit dem eingezeichneten Koordinatensystem (x,y,z) gilt:

Gitterpunkte der 1. BZ des fcc-Gitters: (0, 0, 0); (1, 1, 1); (−1, 1, 1); (−1, −1, 1); (1, −1, 1); (1, 1, −1); (−1, 1, −1); (−1, −1, −1); (1, −1, −1)
Γ-Punkt (0, 0, 0): Das Zentrum der 1. BZ
X-Punkt (0, 1, 0): Der Schnittpunkt der Achse [010] mit dem Rand der 1. BZ
L-Punkt (0.5, 0.5, 0.5): Der Schnittpunkt der Raumdiagonale [111] mit dem Rand der 1. BZ
K-Punkt (0.75, 0.75, 0): Der Schnittpunkt der Diagonalen in einer Ebene [110] mit dem Rand der 1. BZ
U-Punkt (0.25, 1, 0.25)
W-Punkt (0.5, 1, 0)

Anwendung

In der Festkörperphysik wird der Kristallimpuls $\hbar {\vec k}$ eines Teilchens oder Quasiteilchens (z.B. Elektron und Loch und andere) als Vektor im reziproken Gitter angegeben. Ein Quasiteilchen mit einem bestimmten Wellenvektor ${\vec k}_{1}$ verhält sich exakt genauso wie eines, dessen Wellenvektor ${\vec k}_{2}$ sich von ${\vec k}_{1}$ um einen reziproken Gittervektor $\vec K$ unterscheidet. Daher braucht man für Größen, die vom Kristallimpuls abhängen, nur die Werte für Kristallimpulse innerhalb der ersten Brillouin-Zone zu bestimmen. Der Hintergrund ist, dass Wellen (Teilchenwellen) an sog. Bragg-Ebenen zurückgestreut werden ${\vec k}_{1}={\vec k}_{2}+{\vec K}$ (siehe auch Laue-Bedingung).

Literatur

Charles Kittel: Einführung in die Festkörperphysik. 10. Auflage. Oldenbourg, München 1993, ISBN 3-486-22716-5.
Konrad Kopitzki: Einführung in die Festkörperphysik. 6. Auflage. Teubner, Wiesbaden 2007, ISBN 3-8351-0144-7.

Basierend auf einem Artikel in:

Wikipedia.de