Deformationsinvarianten

Die Deformationsinvarianten $I_{1},I_{2},I_{3}$ bezeichnen in der Kontinuumsmechanik die drei Hauptinvarianten des rechten oder linken Cauchy-Green Deformationstensors. Sie stellen die Koeffizienten des charakteristischen Polynoms bei Hauptachsentransformation des Strecktensors dar. Gleichzeitig lassen sie sich nach dem Satz von Vieta auch durch die Hauptstreckungen $\lambda _{1},\lambda _{2},\lambda _{3}$ ausdrücken:

${\begin{array}{lclcl}I_{1}&=&\mathrm {Spur} (\mathbf {b} )&=&\lambda _{1}^{2}+\lambda _{2}^{2}+\lambda _{3}^{2}\\I_{2}&=&\mathrm {Spur} (\mathbf {b} ^{-1})\,\det(\mathbf {b} )&=&\lambda _{1}^{2}\,\lambda _{2}^{2}+\lambda _{1}^{2}\,\lambda _{3}^{2}+\lambda _{2}^{2}\,\lambda _{3}^{2}\\I_{3}&=&\det(\mathbf {b} )&=&\lambda _{1}^{2}\,\lambda _{2}^{2}\,\lambda _{3}^{2}\end{array}}$

mit

$\mathbf{b}$ der Deformationstensor
$\mathrm {Spur} (\mathbf {b} )$ der Spur des Deformationstensors,
$\det(\mathbf {b} )$ der Determinante des Deformationstensors,
$\mathbf {b} ^{-1}$ der Inversen des Deformationstensors und
$\lambda _{1,2,3}^{2}=\eta _{1,2,3}$ der Eigenwerte des Deformationstensors.

Obige Zusammenhänge gelten für den linken Cauchy-Green Tensor $\mathbf {b} :=\mathbf {F\cdot F^{\top }}$ und den rechten Cauchy-Green Tensor $\mathbf {C} :=\mathbf {F^{\top }\cdot F}$ , denn beide Tensoren haben wegen

$\mathbf {b} \cdot {\vec {v}}=\eta {\vec {v}}\quad \Leftrightarrow \quad \mathbf {F^{\top }\cdot b} \cdot {\vec {v}}=\mathbf {F^{\top }\cdot F\cdot F^{\top }} \cdot {\vec {v}}=\mathbf {C\cdot (F^{\top }} \cdot {\vec {v}})=\eta (\mathbf {F^{\top }} \cdot {\vec {v}})$

Veranschaulichung der Polarzerlegung

dieselben Eigenwerte und damit auch dieselben Invarianten, was sie einander mathematisch ähnlich macht. Der Tensor F ist der Deformationsgradient. Gleiches gilt für die symmetrischen, positiv definiten, rechten und linken Deformationstensoren U bzw. v, die sich gemäß

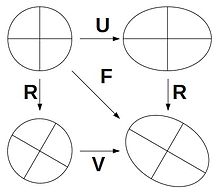
$\mathbf {F} =\mathbf {R\cdot U} =\mathbf {v\cdot R} .$

aus der Polarzerlegung des Deformationsgradienten ergeben, siehe Bild. Darin ist R ein eigentlich orthogonaler Tensor mit den Eigenschaften R^T · R = 1 und det(R) = +1 (1 ist der Einheitstensor.) Der rechte und linke Deformationstensor haben wegen

$\mathbf {v} \cdot {\vec {v}}=\lambda {\vec {v}}\quad \Leftrightarrow \quad \mathbf {b} \cdot {\vec {v}}=\mathbf {F\cdot F^{\top }} \cdot {\vec {v}}=\mathbf {v\cdot R\cdot R^{\top }\cdot v^{\top }} \cdot {\vec {v}}=\lambda \mathbf {v} \cdot {\vec {v}}=\lambda ^{2}{\vec {v}}$

die Hauptstreckungen λ_1,2,3 als Eigenwerte, denn sie sind ebenfalls einander ähnlich:

$\mathbf {R^{\top }\cdot v} \cdot {\vec {v}}=\mathbf {R^{\top }\cdot v\cdot R\cdot R^{\top }} \cdot {\vec {v}}=\mathbf {R^{\top }\cdot R\cdot U\cdot R^{\top }} \cdot {\vec {v}}=\mathbf {U\cdot (R^{\top }} \cdot {\vec {v}})=\lambda (\mathbf {R^{\top }} \cdot {\vec {v}}).$

Weil der Deformationsgradient immer und überall invertierbar ist, sind dies die Strecktensoren auch.

Die dritte Invariante stellt gleichzeitig das Quadrat des Volumenverhältnisses $J:=\operatorname {det} (\mathbf {F} )$ dar:

$I_{3}(\mathbf {b} )=I_{3}(\mathbf {C} )=J^{2}=I_{3}^{2}(\mathbf {v} )=I_{3}^{2}(\mathbf {U} ).$

Bei Inkompressibilität im Werkstoffverhalten ( J=1 ) bleibt also die dritte Invariante der Strecktensoren gleich der Identität.

Basierend auf einem Artikel in:

Wikipedia.de