Limes (Kategorientheorie)
In der Algebra oder allgemeiner der Kategorientheorie ist der projektive Limes (oder inverse Limes oder einfach Limes) eine Konstruktion, mit der man verschiedene in gewisser Weise zusammengehörende Strukturen verbinden kann. Das Ergebnis dieses Verbindungsvorgangs wird vor allem bestimmt von Abbildungen zwischen diesen Strukturen.
Projektive Limites für Mengen und einfache algebraische Strukturen
Die folgende Konstruktion definiert den Limes für Mengen oder beliebige algebraische Strukturen, die mithilfe von Limites (Produkten, Endobjekten, Differenzkernen) definiert sind. Als Beispiel werden Gruppen behandelt.
Gegeben seien eine halbgeordnete
Menge ,
für jedes
eine Gruppe
und für je zwei Indizes
mit
ein Gruppenhomomorphismus
Diese Homomorphismen seien außerdem verträglich in dem Sinne, dass für
gilt:
(„um von
nach
zu kommen, kann man auch einen Umweg über
nehmen“).
Der projektive Limes
ist die Menge aller Familien
mit
mit der Eigenschaft
für
.
Durch die komponentenweise Definition seiner Verknüpfung über die
Verknüpfungen in den Komponenten
wird
zu einer Gruppe.
Die universelle Eigenschaft
Der projektive Limes
zusammen mit den Homomorphismen
den kanonischen Projektionen, hat die folgende universelle Eigenschaft:
- Für jede Gruppe
und Homomorphismen
, für die
für alle
gilt, existiert ein eindeutig bestimmter Homomorphismus
, so dass
gilt.
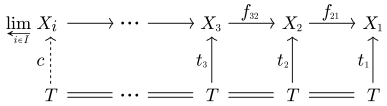
- Kommutatives Diagramm zur Definition des Limes in der Kategorientheorie
Projektive Limites in beliebigen Kategorien
Mithilfe des Begriffs des projektiven Limes für Mengen kann man projektive
Limites in beliebigen Kategorien definieren: Sind Objekte
einer Kategorie
und Übergangsmorphismen
gegeben, so ist der Limes dieses projektiven Systems charakterisiert durch eine
natürliche Äquivalenz
von Funktoren
in ;
dabei ist der Limes auf der rechten Seite der bereits definierte Limesbegriff
für Mengen. Der derartig definierte Limes erfüllt die analoge universelle
Eigenschaft.
Für "einfache" algebraische Strukturen wie Vektorräume, Gruppen oder Ringe stimmt dieser Limesbegriff mit dem oben definierten, mengenbasierten überein.
Es gibt jedoch Kategorien, in denen projektive Limites nicht existieren,
beispielsweise die Kategorie der endlichen abelschen Gruppen: Es sei
das projektive System
mit der Projektion auf die ersten Faktoren als Übergangsabbildungen. Für
ist
unendlich, also nicht gleich
für irgendeine endliche abelsche Gruppe .
Beispiele
- In der Kategorie der topologischen
Räume gibt es Limites: Der mengenbasierte Limes war konstruiert als eine
Teilmenge des kartesischen Produktes. Versieht man das Produkt mit der Produkttopologie und
den Mengen-Limes mit der Teilraumtopologie, erhält man den kategoriellen
Limes. Sind alle
kompakt und hausdorffsch, dann ist der projektive Limes
ebenfalls kompakt und hausdorffsch.
- Jede kompakte topologische Gruppe ist projektiver Limes von kompakten Lie-Gruppen.
- Für
ist der Ring
der p-adischen ganzen Zahlen der projektive Limes der Restklassenringe
, wobei die halbgeordnete Indexmenge
mit der natürlichen Ordnung versehen ist und die Morphismen die Restklassenabbildungen sind. Die natürliche Topologie auf
ist die von der diskreten Topologie auf den
induzierte Produkttopologie, und
ist dicht in
.
-
→ Hauptartikel: Proendliche Zahl
- Die proendliche
Vervollständigung
des Rings der ganzen Zahlen
ist der projektive Limes der Restklassenringe
, wobei die Indexmenge
mit der Halbordnung der Teilbarkeit versehen ist und die Morphismen die Restklassenabbildungen sind. Genauer: Sind
mit
, dann sind die Restklassenabbildungen
wie oben ein verträgliches System von Homomorphismen.
erweist sich als das direkte Produkt
(Addition und Multiplikation gehen komponentenweise – letztere mit Nullteilern).
Die natürliche Topologie aufist die von der diskreten Topologie auf den
induzierte Produkttopologie, und
ist dicht in
.
| Beweis der Dichtheit von |
|---|
|
Für die Zwecke des Beweises werden die Primzahlen durchnummeriert:
|
- Für eine beliebige galoissche
Körpererweiterung
ist die Galoisgruppe
isomorph zum projektiven Limes der Galoisgruppen
, wobei
alle endlichen und galoisschen Zwischenerweiterungen von
durchläuft, die halbgeordnete Indexmenge die Menge dieser Zwischenkörper mit der Inklusionsordnung ist, und der Morphismus für
gegeben ist durch
(also die Einschränkung eines Automorphismus auf den kleineren Körper). Betrachtet man alle
als diskrete topologische Gruppen, dann wird auf
eine Produkttopologie induziert, die Krulltopologie genannt wird.
Da alle endlichen Erweiterungen eines endlichen Körpers zyklisch sind, ist die Galoisgruppe des algebraischen Abschlusses eines endlichen Körpers isomorph zu(als additiver Gruppe).
- Erweiterungssatz
von Kolmogorov: Gegeben sei eine nichtleere Indexmenge
und Borel’sche Räume
für
. Sei
die Menge aller nichtleeren, endlichen Teilmengen von
. Ist eine projektive Familie von Wahrscheinlichkeitsmaßen
gegeben, so existiert ein eindeutig bestimmtes Wahrscheinlichkeitsmaß
auf dem Messraum
für das
für jedes
gilt. Dabei bezeichnet
die Projektion auf die Komponenten der Indexmenge
. Man schreibt dann
und bezeichnet das Wahrscheinlichkeitsmaß
dann als projektiven Limes.
Limites mit Indexkategorien
In Verallgemeinerung des Limes für teilgeordnete Indexmengen kann man Limites für beliebige Indexkategorien betrachten:
Es sei
eine kleine
Kategorie,
eine beliebige Kategorie und
ein Funktor. Dann ist ein Limes von
ein darstellendes
Objekt für den Funktor
dabei bezeichne
den konstanten Funktor
mit Wert
.
Der Limes ist also ein Objekt
zusammen mit einer natürlichen Äquivalenz
von Funktoren in .
Aus dieser natürlichen Äquivalenz erhält man für
auch die kanonischen Projektionen
(als Entsprechung von
auf der linken Seite).
Die natürliche Äquivalenz ist im Wesentlichen nur eine kompakte Schreibweise der universellen Eigenschaft: Morphismen in ein Limesobjekt entsprechen kompatiblen Systemen von Morphismen in die einzelnen Objekte, genau wie im Spezialfall von teilgeordneten Indexmengen.
Dieser Limesbegriff umfasst einige andere universelle Konstruktionen als Spezialfälle:
| universelle Konstruktion | |
|---|---|
| Beliebig viele Objekte, nur Identitäten | Produkt |
| Endobjekt | |
| Differenzkern | |
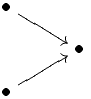 |
Faserprodukt |
Hat die Indexkategorie ein Anfangsobjekt
,
so ist der Limes gleich
.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 18.03. 2023