Catalanischer Körper
Ein catalanischer Körper oder auch dual-archimedischer Körper ist ein Körper, der sich zu einem archimedischen Körper dual verhält. So ist zum Beispiel das Rhombendodekaeder dual zum Kuboktaeder. Benannt sind die catalanischen Körper – von denen es 13 gibt – nach dem belgischen Mathematiker Eugène Charles Catalan. Die catalanischen Körper sind konvexe Polyeder.
Ein catalanischer Körper hat nur eine Art von Seitenflächen, d.h. sämtliche Seitenflächen sind zueinander kongruent. Die Seitenflächen sind nichtregelmäßige Vielecke. Andererseits gibt es mindestens zwei verschiedene Arten von Ecken (das Rhombendodekaeder hat zum Beispiel Ecken, an die drei Rhomben, und solche, an die vier Rhomben grenzen). Bei den archimedischen Körpern verhält es sich andersherum: Sie haben eine Art von Ecken und mehrere Arten von Seitenflächen.
Allen catalanischen Körpern ist gemein, dass sie eine Inkugel, die sämtliche Flächen von innen berührt, aufweisen. Außerdem existiert eine Kantenkugel, die sämtliche Kanten von innen berührt. Alle Diederwinkel eines catalanischen Körpers sind gleich.
Eine charakteristische Eigenschaft der catalanischen Körper ist die Uniformität der Flächen. Das heißt: Sind A, B zwei beliebige Seitenflächen, dann kann man den Körper so drehen oder spiegeln, dass der Körper in sich und die Seite A in die Seite B überführt wird. Diese Eigenschaft folgt aus der Uniformität der Ecken für archimedische Körper.
| Catalanischer Körper | Bild | Dualer Körper | Flächen | Ecken | Kanten | Flächenform | Symmetrie |
|---|---|---|---|---|---|---|---|
| Triakistetraeder | 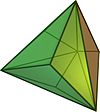 |
Tetraederstumpf | 12 | 8 | 18 | gleichschenkliges Dreieck | |
| Rhombendodekaeder | 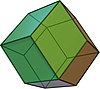 |
Kuboktaeder | 12 | 14 | 24 | Rhombus | |
| Tetrakishexaeder |  |
Oktaederstumpf | 24 | 14 | 36 | gleichschenkliges Dreieck | |
| Triakisoktaeder | 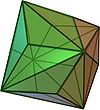 |
Hexaederstumpf | 24 | 14 | 36 | gleichschenkliges Dreieck | |
| Deltoidalikositetraeder |  |
Rhombenkuboktaeder | 24 | 26 | 48 | Deltoid | |
| Pentagonikositetraeder (zwei spiegelbildlich entgegengesetzte Varianten) |
  |
abgeschrägtes Hexaeder | 24 | 38 | 60 | allgemeines Fünfeck | |
| Hexakisoktaeder
oder Disdyakisdodekaeder |
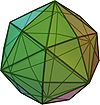 |
Kuboktaederstumpf | 48 | 26 | 72 | unregelmäßiges Dreieck | |
| Rhombentriakontaeder | 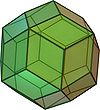 |
Ikosidodekaeder | 30 | 32 | 60 | Rhombus | |
| Pentakisdodekaeder |  |
Ikosaederstumpf | 60 | 32 | 90 | gleichschenkliges Dreieck | |
| Triakisikosaeder |  |
Dodekaederstumpf | 60 | 32 | 90 | gleichschenkliges Dreieck | |
| Deltoidalhexakontaeder |  |
Rhombenikosidodekaeder | 60 | 62 | 120 | Deltoid | |
| Pentagonhexakontaeder (zwei spiegelbildlich entgegengesetzte Varianten) |
  |
abgeschrägtes Dodekaeder | 60 | 92 | 150 | allgemeines Fünfeck | |
| Hexakisikosaeder
oder Disdyakistriakontaeder |
 |
Ikosidodekaederstumpf | 120 | 62 | 180 | unregelmäßiges Dreieck |
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 08.08. 2023