Normalenbündel

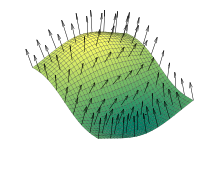
Normalenvektoren an einer Fläche im dreidimensionalen Raum

Das Normalenbündel ist ein Begriff aus der Differentialtopologie und der Differentialgeometrie, Teilgebieten der Mathematik. Ein solches Vektorbündel umfasst alle Normalenvektoren einer Untermannigfaltigkeit und ist somit ein zum Tangentialbündel komplementäres Konzept.

Mit Hilfe von Normalenbündeln können beispielsweise tubulare Umgebungen von Untermannigfaltigkeiten konstruiert werden.

Definition

Untermannigfaltigkeit

Das Normalenbündel einer differenzierbaren Untermannigfaltigkeit $Y\subset X$ ist das Vektorbündel über , das aus allen Paaren $(y,\nu )$ besteht, wobei $y\in Y$ gilt und $\nu$ ein Vektor im Quotientenraum $T_{y}X/T_{y}Y$ ist, wobei $T_{y}X$ und $T_{y}Y$ die Tangentialräume von und sind. Mit anderen Worten ist das Normalenbündel definiert als die disjunkte Vereinigung

$NY:=\coprod _{y\in Y}T_{y}X/T_{y}Y$ .

Immersierte Untermannigfaltigkeit

Etwas allgemeiner ist die Konstruktion des normalen Bündels einer immersierten Untermannigfaltigkeit. Sei also $f\colon Y\to X$ eine Immersion von in . Dann ist das Normalenbündel von definiert durch

$NY:=\coprod _{y\in Y}f^{*}(T_{y}X)/T_{y}Y$ ,

wobei $f^{*}$ der Rücktransport von ist.

Riemannsche Geometrie

Seien und riemannsche Mannigfaltigkeiten und $f\colon Y\to X$ eine Immersion, so dass eine in immersierte Mannigfaltigkeit ist. Sei $p\in Y$ und $T_{p}X$ der Tangentialraum von in . Aufgrund der riemannschen Metrik gibt es eine orthogonale Zerlegung $T_{p}X=T_{p}Y\oplus N_{p}Y$ dieses Tangentialraums. Dabei ist $N_{p}Y$ der Normalenraum am Punkt . Die Menge

$NY:=\coprod _{p\in Y}N_{p}Y$

ist das Normalenbündel der riemannschen Mannigfaltigkeit bezüglich . Dieses Normalenbündel in der riemannschen Geometrie ist ein Spezialfall der zuvor genannten Definition, denn $N_{p}Y$ ist offenbar zu den Quotientenräumen obiger Definition isomorph.

Stabiles Normalenbündel

→ Hauptartikel: Stabiles Normalenbündel

Abstrakte differenzierbare Mannigfaltigkeiten haben ein kanonisches Tangentenbündel, aber kein Normalenbündel. Nur das Einbetten (oder Immersieren) einer Mannigfaltigkeit in eine andere ergibt ein normales Bündel.

Da allerdings jede differenzierbare Mannigfaltigkeit nach dem Einbettungssatz von Whitney in $\mathbb {R} ^{N}$ eingebettet werden kann, lässt jede Mannigfaltigkeit bei einer solchen Einbettung ein Normalenbündel zu. Es gibt im Allgemeinen keine natürliche Wahl der Einbettung, aber für eine gegebene Mannigfaltigkeit sind zwei beliebige Einbettungen in $\mathbb {R} ^{N}$ für ausreichend großes isotop und induzieren daher das gleiche Normalenbündel. Die resultierende Klasse der Normalenbündel (es handelt sich um eine Klasse von Bündeln und nicht um ein bestimmtes Bündel, da variieren kann) wird als stabiles Normalenbündel bezeichnet.

Basierend auf einem Artikel in:

Wikipedia.de