Immersierte Mannigfaltigkeit

Eine immersierte Mannigfaltigkeit oder immersierte Untermannigfaltigkeit ist ein Objekt aus dem mathematischen Teilgebiet der Differentialtopologie. Seltener wird dieses Objekt auch immergierte Mannigfaltigkeit genannt, im Englischen spricht man meistens von einer immersed submanifold.^[1]

Hat man eine differenzierbare Abbildung $f\colon S\to M$ zwischen zwei Mannigfaltigkeiten, so ist das Bild f(S) im Allgemeinen keine Untermannigfaltigkeit von . Falls die Ableitung von jedoch injektiv ist, ist f(S) eine Mannigfaltigkeit, die aber keine (eingebettete) Untermannigfaltigkeit von sein muss. Dieses Objekt wird immersierte Mannigfaltigkeit genannt.

Definition

Seien und differenzierbare Mannigfaltigkeiten. Dann ist eine immersierte Mannigfaltigkeit von das Bild ${\tilde {S}}:=\psi (S)$ der Immersion $\psi \colon S\to M$ . Die Topologie auf $\tilde{S}$ muss so gewählt werden, dass $\psi$ stetig ist. Oftmals wird noch gefordert, dass die Immersion $\psi$ injektiv sein muss.

Als Menge ist ${\tilde {S}}$ eine Teilmenge von , jedoch ist es im Allgemeinen keine Untermannigfaltigkeit von . Das heißt, die Topologie von $\tilde{S}$ entspricht hier auch nicht der Teilraumtopologie und insbesondere sind auch die differenzierbaren Strukturen von $\tilde{S}$ und nicht kompatibel. Ist jedoch $\psi \colon S\hookrightarrow M$ eine differenzierbare Einbettung, so ist $\tilde{S}$ tatsächlich eine Untermannigfaltigkeit.

Unterscheidung zur Untermannigfaltigkeit

Es gibt zwei Gründe, aus denen die immersierte Mannigfaltigkeit keine Untermannigfaltigkeit sein muss:

Die Immersion $\psi$ ist nicht injektiv, die Immersion schneidet sich selbst. (s. Abbildung 1)
Selbst wenn die Immersion $\psi$ injektiv ist, kann es sein, dass die Abbildung kein Homöomorphismus ist, da das Bild offener Enden inneren Punkten von ${\tilde {S}}$ beliebig nahe kommen kann, so dass die Topologie von ${\tilde {S}}$ nicht mit der von übereinstimmt. (s. Abb. 2) Dieser Effekt kann nur für nichtkompakte auftreten, für kompakte Mannigfaltigkeiten ist eine injektive Immersion $S\to M$ stets eine Einbettung.

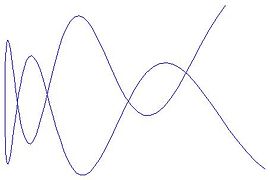
Abb. 1: Reelle Zahlengerade immersiv abgebildet in die Ebene mit Selbstschnitten

Abb. 2: Offenes Intervall injektiv und immersiv abgebildet, so dass die offenen Enden auf die mit Pfeilen markierten Enden abgebildet werden

Beispiel

Die Kurve $\gamma \colon ]-{\tfrac {\pi }{2}},{\tfrac {3\pi }{2}}[\to \mathbb {R} ^{2}$ , die durch $t\mapsto (\sin(2t),\cos(t))$ definiert ist, ist eine injektive Immersion. Daher ist ihr Bild eine immersierte Mannigfaltigkeit.
Eine Lie-Gruppe ist sowohl eine Gruppe im Sinne der Algebra also auch eine glatte Mannigfaltigkeit, wobei die beiden Strukturen miteinander verträglich sind. Eine Lie-Untergruppe ist eine Untergruppe der Lie-Gruppe, die ebenfalls wieder die Struktur einer glatten Mannigfaltigkeit trägt, die mit der Gruppenstruktur verträglich ist. Diese Lie-Untergruppe ist im Allgemeinen keine Untermannigfaltigkeit, aber eine immersierte (Unter)Mannigfaltigkeit, wobei die Immersion injektiv ist. Ein konkretes Beispiel ist eine Kurve irrationalen Anstiegs im Torus. Diese ist eine Untergruppe und eine immersierte Untermannigfaltigkeit, aber nicht eingebettet: ihr Bild liegt dicht im Torus.

Literatur

Herbert Amann, Joachim Escher: Analysis. 2. Band 2. korrigierte Auflage. Birkhäuser-Verlag, Basel u. a. 2006, ISBN 3-7643-7105-6.

Anmerkungen

↑ Die korrekte Ableitung aus dem Lateinischen ist eigentlich "immergierte Mannigfaltigkeit", im Deutschen hat sich aber das aus dem englischen "immersed manifold" abgeleitete "immersierte Mannigfaltigkeit" in jüngerer Zeit als häufigere Variante durchgesetzt.

Basierend auf einem Artikel in:

Wikipedia.de