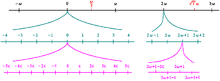
Hyperreelle Zahl
In der Mathematik sind
hyperreelle Zahlen ein zentraler Untersuchungsgegenstand der Nichtstandardanalysis.
Die Menge der hyperreellen Zahlen wird meist als
geschrieben; sie erweitert die reellen Zahlen um infinitesimal benachbarte
Zahlen sowie um unendlich große (infinite) Zahlen.
Als Newton und Leibniz ihre Differentialrechnung mit „Fluxionen“ bzw. „Monaden“ durchführten, benutzten sie infinitesimale Zahlen, und noch Euler und Cauchy fanden sie nützlich. Trotzdem wurden diese Zahlen von Anfang an skeptisch betrachtet, und im 19. Jahrhundert wurde die Analysis durch die Einführung der epsilon-delta-Definition des Grenzwertes und die Definition der reellen Zahlen durch Cauchy, Weierstraß und andere auf eine strenge Grundlage gestellt, die ohne infinitesimale Größen auskommt.
Abraham Robinson zeigte dann in den 1960er Jahren, auf welche Weise unendlich große und kleine Zahlen streng formal definiert werden können, und eröffnete so das Gebiet der Nichtstandardanalysis. Die hier gegebene Konstruktion ist eine vereinfachte, aber nicht minder strenge Version, die zuerst von Lindstrom gegeben wurde.
Durch die hyperreellen Zahlen ist eine Formulierung der Differential- und Integralrechnung ohne den Grenzwertbegriff möglich.
Elementare Eigenschaften
Die hyperreellen Zahlen
bilden einen geordneten
Körper,
der
als Teilkörper enthält. Beide sind reell
abgeschlossen.
Der Körper
wird so konstruiert, dass er elementar
äquivalent zu
ist. Das bedeutet, dass jede Aussage, die in
gilt, auch in
gilt, falls die Aussage sich in der Prädikatenlogik
erster Stufe über der Signatur
formulieren lässt.
Die Signatur bestimmt, welche Symbole man in den Aussagen gebrauchen darf.
Die Einschränkung auf die Prädikatenlogik erster Stufe bedeutet, dass man
nur über Elemente des Körpers quantifizieren kann, nicht jedoch über Teilmengen.
Folgende Aussagen gelten z.B. sowohl in
als auch in
:
- Jede Zahl, die größer oder gleich Null ist, hat eine Quadratwurzel. In
Formeln:
Das heißt nun nicht, dass
und
sich genau gleich verhalten; sie sind nicht isomorph. Zum Beispiel gibt es
in
ein Element
,
das größer als alle natürlichen Zahlen ist. Dies lässt sich jedoch nicht durch
eine Aussage der obigen Form ausdrücken, man braucht dazu unendlich
viele:
Eine solche Zahl gibt es in
nicht. Eine hyperreelle Zahl wie
nennt man infinit oder unendlich, der Kehrwert einer unendlich großen
Zahl ist eine infinitesimale Zahl.
Ein weiterer Unterschied: Die reellen Zahlen sind ordnungsvollständig,
d. h. jede nichtleere, nach oben beschränkte Teilmenge von
besitzt ein Supremum
in
.
Diese Forderung charakterisiert die reellen Zahlen als geordneten Körper
eindeutig, d.h. bis auf eindeutige Isomorphie.
ist hingegen nicht ordnungsvollständig: Die Menge aller endlichen Zahlen in
besitzt kein Supremum, ist aber z.B. durch obiges
beschränkt. Das liegt daran, dass man zur Formulierung der
Ordnungsvollständigkeit über alle Teilmengen quantifizieren muss; sie kann daher
nicht in der Prädikatenlogik erster Stufe formalisiert werden.
Die hyperreellen Zahlen sind gleichmächtig zu den reellen Zahlen:
Konstruktion
Die Menge aller Folgen
reeller Zahlen ()
bilden eine Erweiterung der reellen Zahlen, wenn man die reellen Zahlen mit den
konstanten Folgen identifiziert.
wird also mit der Folge
,
wird also mit der Folge
identifiziert.
Die Prototypen für „unendliche große“ Zahlen sind in dieser Menge Folgen, die irgendwann größer als jede reelle Zahl werden, z.B. die Folge:
Auf
kann man nun die Addition und Multiplikation gliedweise definieren:
Dadurch wird
zu einem kommutativen
unitären
Ring, allerdings besitzt dieser Nullteiler und ist daher kein Körper. Es
gilt z.B. für
die Gleichung
,
obwohl sowohl
als auch
ungleich null sind. Es müssen daher noch Folgen über eine Äquivalenzrelation
identifiziert werden. Die Idee ist, dass Folgen äquivalent sind, wenn die Menge
aller Stellen, wo sich die Folgen unterscheiden, eine unwesentliche ist.
Was ist nun die Menge aller unwesentlichen Mengen? Insbesondere sollen ja
Folgen äquivalent sein, wenn sie sich im Unendlichen gleich verhalten,
wenn sie also nur an endlich vielen Stellen verschieden sind. Alle endlichen
Mengen sind daher unwesentlich. Und das Beispiel mit
und
zeigt, dass für jede Teilmenge entweder die Teilmenge oder ihr Komplement
unwesentlich ist. Unter anderem wird dann noch gebraucht, dass die Vereinigung
zweier unwesentlicher Mengen unwesentlich ist, da die Äquivalenzrelation
transitiv sein muss. Das führt zu einem Ultrafilter:
Ein Filter
auf den natürlichen Zahlen ist eine Menge von Teilmengen der natürlichen Zahlen,
für die gilt:
- Die leere Menge liegt nicht in
.
- Wenn sie zwei Mengen enthält, dann auch deren Schnittmenge.
- Wenn sie eine Menge enthält, dann auch deren Obermengen.
Ein Filter
ist frei, wenn gilt:
enthält keine endlichen Mengen
Er ist ein Ultrafilter, falls gilt:
- Wenn
eine bestimmte Teilmenge nicht enthält, enthält
deren Komplement.
Die Existenz eines freien Ultrafilters folgt aus dem Lemma von Zorn. Mit
Hilfe dieses Ultrafilters
lässt sich eine Äquivalenzrelation definieren:
, falls
.
Auf der Menge der Äquivalenzklassen,
die mit
bezeichnet wird, kann nun die Addition und Multiplikation der Äquivalenzklassen
über Repräsentanten definiert werden. Dies ist wohldefiniert, da
ein Filter ist. Da
sogar ein Ultrafilter ist, hat jedes Element außer 0 in
ein Inverses. Z.B. ist eine der beiden Folgen
und
äquivalent zu null, die andere zu eins.
Nun müssen wir auf
noch eine Ordnung definieren. Dies geschieht durch
, falls
.
Leicht wird klar, dass dieses eine totale Ordnung auf
definiert (für die Totalität ist wichtig, dass
ein Ultrafilter ist).
Die Äquivalenzklasse der Folge
ist größer als jede reelle Zahl, denn für eine reelle Zahl
gilt
Anschließend ist noch zu zeigen, dass der konstruierte Körper tatsächlich
elementar äquivalent zu
ist. Dies geschieht durch einen Induktionsbeweis
über den Aufbau der Formeln, wobei von den Ultrafilter-Eigenschaften Gebrauch
gemacht wird.
Bemerkungen
- Jedem Filter auf den natürlichen Zahlen entspricht ein Ideal des Ringes
(aber nicht umgekehrt). Einem Ultrafilter entspricht dabei ein maximales Ideal, daher ist der Quotient ein Körper. Die Wahl eines nicht-freien Ultrafilters hätte zur Folge, dass der Körper der Äquivalenzklassen isomorph zum Ausgangskörper ist.
- Diese Konstruktion ist ein Spezialfall der Ultrapotenz. Unter
anderem heißt das, dass die Einbettung von
in
eine elementare Einbettung ist und dass
-saturiert ist.
- Aus den Axiomen der Mengenlehre (ZFC) plus der Kontinuumshypothese folgt, dass diese Konstruktion nicht von der Wahl des Ultrafilters abhängt. (Das bedeutet, dass unterschiedliche Ultrafilter zu isomorphen Ultraprodukten führen.)
Infinitesimale und unendlich große Zahlen
Eine hyperreelle Zahl heißt infinitesimal, wenn sie kleiner als jede
positive reelle Zahl und größer als jede negative reelle Zahl ist. Die Zahl Null ist die einzige
infinitesimale reelle Zahl, aber es gibt andere hyperreelle infinitesimale
Zahlen, beispielsweise .
Sie ist größer als null, aber kleiner als jede positive reelle Zahl, denn der
Ultrafilter enthält alle Komplemente endlicher Mengen.
Eine negativ infinitesimale Zahl ist größer als jede negative reelle
Zahl und kleiner als jede positive reelle Zahl, z.B..
Eine hyperreelle Zahl
heißt endlich, wenn es eine natürliche Zahl
gibt mit
,
anderenfalls heißt
unendlich. Die Zahl
ist eine infinite Zahl. Beachte: Die Bezeichnung „unendlich groß“ bezeichnet
meist eine Zahl, die größer ist als jede natürliche Zahl, „unendlich“ schließt
aber auch Zahlen ein, die kleiner sind als jede ganze Zahl, wie
.
Eine von 0 verschiedene Zahl
ist genau dann unendlich, wenn
infinitesimal ist. Zum Beispiel ist
.
Es lässt sich zeigen, dass jede endliche hyperreelle Zahl „sehr nah“ an genau
einer reellen Zahl liegt. Genauer: Ist
eine endliche hyperreelle Zahl, dann gibt es genau eine reelle Zahl
,
so dass
infinitesimal ist. Die Zahl
nennt man den Standardteil von
,
die Differenz zu
ist der Nichtstandardteil. Die Abbildung st hat einige angenehme
Eigenschaften: Für alle endlichen hyperreellen Zahlen
,
gilt:
genau dann, wenn
reell ist
Wobei das insbesondere bedeutet, dass der Term auf der linken Seite definiert
ist, dass also z.B.
endlich ist, falls sowohl
als auch
endlich sind. Die Menge der endlichen Zahlen bilden also einen Unterring in den
hyperreellen Zahlen. Außerdem ist
, falls
nicht infinitesimal ist,
Ferner gilt:
- Die Abbildung st ist stetig bzgl. der Ordnungstopologie auf der Menge der endlichen hyperreellen Zahlen, sie ist sogar lokal konstant.
Die ersten zwei Eigenschaften (und die Folgerung
aus der dritten Eigenschaft) besagen, dass st ein Ring-Homomorphismus ist.
Zum Beispiel ist die hyperreelle Zahl
gliedweise kleiner als
,
also ist
.
Sie ist aber größer als jede reelle Zahl kleiner 1. Sie ist daher zur 1
infinitesimal benachbart und 1 ist ihr Standardteil. Ihr
Nichtstandardteil (die Differenz zu 1) ist
.
Beachte aber, dass die reelle Zahl
als Grenzwert
der Folge
gleich 1 ist.
Weitere Eigenschaften
Die hyperreellen Zahlen sind gleichmächtig zu den
reellen Zahlen, denn die Mächtigkeit muss mindestens so groß wie die der reellen
Zahlen sein, da sie die reellen Zahlen enthalten, und kann höchstens so groß
sein, da die Menge
gleichmächtig zu den reellen Zahlen ist. Die Ordnungsstruktur der hyperreellen
Zahlen hat überabzählbare
Konfinalität,
d.h. es existiert keine unbeschränkte abzählbare
Menge, also keine unbeschränkte Folge von hyperreellen Zahlen: Sei eine Folge
von hyperreellen Zahlen durch Repräsentanten
gegeben. Dann ist die hyperreelle Zahl mit dem Repräsentanten
,
eine obere Schranke. Es lassen sich also mit keiner Folge beliebig große hyperreelle Zahlen erreichen. Die Ordnung der hyperreellen Zahlen induziert eine Ordnungstopologie. Mittels dieser lassen sich die üblichen topologischen Begriffe von Grenzwerten und Stetigkeit auf die hyperreellen Zahlen übertragen. Als geordneter Körper weisen sie mit der Addition eine mit der Topologie verträgliche Gruppenstruktur auf, es handelt sich also um eine topologische Gruppe. Diese induziert eine uniforme Struktur, sodass man auf den hyperreellen Zahlen auch von gleichmäßiger Stetigkeit, Cauchyfiltern etc. sprechen kann. Aus der überabzählbaren Konfinalität folgt durch Betrachtung von Kehrwerten, dass es auch keine Folge bestehend aus von 0 (oder entsprechend einer beliebigen anderen hyperreellen Zahl) verschiedenen hyperreellen Zahlen gibt, die beliebig nah an die 0 gelangt. Daher erfüllt die Topologie der hyperreellen Zahlen nicht die beiden Abzählbarkeitsaxiome, sie ist also insbesondere nicht metrisierbar. Aus der überabzählbaren Konfinalität folgt auch, dass sie nicht separabel sind. Aus dem Nichtvorhandensein von Suprema zahlreicher Mengen folgt, dass der Raum total unzusammenhängend und nicht lokalkompakt ist.
Siehe auch
Literatur
- Heinz-Dieter Ebbinghaus et al.: Zahlen. 3. Auflage. Springer, Berlin/Heidelberg 1992, ISBN 3-540-55654-0.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 28.09. 2021