Elliptische Kurve

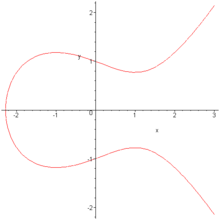
Beispiel einer elliptischen Kurve über dem Körper der reellen Zahlen

In der Mathematik sind elliptische Kurven spezielle algebraische Kurven, auf denen geometrisch eine Addition definiert ist. Diese Addition wird in der Kryptographie zur Konstruktion sicherer Verschlüsselungsmethoden verwendet. Elliptische Kurven spielen aber auch in der reinen Mathematik eine wichtige Rolle. Historisch sind sie durch die Parametrisierung elliptischer Integrale entstanden als deren Umkehrfunktionen (elliptische Funktionen).

Eine elliptische Kurve ist eine glatte algebraische Kurve der Ordnung 3 in der projektiven Ebene. Dargestellt werden elliptische Kurven meist als Kurven in der affinen Ebene, sie besitzen aber noch einen zusätzlichen Punkt im Unendlichen.

Elliptische Kurven über dem Körper der reellen Zahlen können als die Menge aller (affinen) Punkte $(x,y)\in {\mathbb {R}}^{2}$ angesehen werden, die die Gleichung

$y^{2}=x^{3}+ax+b$

erfüllen, zusammen mit einem sogenannten Punkt im Unendlichen (notiert als $\infty$ oder ${\mathcal O}$ ). Die (reellen) Koeffizienten und müssen dabei die Bedingung erfüllen, dass für die Diskriminante des kubischen Polynoms in auf der rechten Seite $-4a^{3}-27b^{2}\neq 0$ gilt, um Singularitäten auszuschließen (die Wurzeln des Polynoms sind dann paarweise verschieden, die Kurve hat keine Doppelpunkte oder andere Singularitäten).

Im Allgemeinen wird man sich bei der Betrachtung der angegebenen Gleichung aber nicht auf den Fall reeller Koeffizienten und Lösungen beschränken, sondern vielmehr den Fall betrachten, dass Koeffizienten und Lösungen aus dem Körper der komplexen Zahlen stammen. Ausführlich untersucht wurden auch elliptische Kurven über dem Körper der rationalen Zahlen, über endlichen Körpern und über p-adischen Körpern. Die Theorie der elliptischen Kurven verbindet daher sehr unterschiedliche Teilgebiete der Mathematik. Die Untersuchung elliptischer Kurven über den rationalen Zahlen oder endlichen Körpern ist Gegenstand der Zahlentheorie und ein Spezialfall der auch in höheren Dimensionen betrachteten Abelschen Varietäten. Ihre Untersuchung über den komplexen Zahlen ist ein klassisches Gebiet der Funktionentheorie.

Jede elliptische Kurve über den komplexen Zahlen kann mit Hilfe eines Gitters in der komplexen Zahlenebene als komplexer Torus dargestellt werden, was sich schon aus der doppelten Periodizität elliptischer Funktionen ergibt (siehe Weierstraßsche elliptische Funktion). Ihre Riemannsche Fläche ist topologisch ein Torus und über die zugehörige Aufteilung der komplexen Ebene durch ein Gitter eine abelsche Gruppe. Diese Gruppenstruktur überträgt sich auch auf elliptischen Kurven über den rationalen Zahlen und auf eine besondere Art von Addition für Punkte auf elliptischen Kurven (siehe unten). Der Mathematiker Andrew Wiles bewies im Jahr 1994 den Modularitätssatz, der besagt, dass alle elliptische Kurven über den rationalen Zahlen durch Modulformen parametrisiert werden. Aus diesem Satz kann der Beweis eines bekannten zahlentheoretischen Problems (Fermats letzter Satz) gefolgert werden.

Praktische Anwendung finden elliptische Kurven in modernen Verschlüsselungsverfahren (Elliptische-Kurven-Kryptosystem), die die oben erwähnte besondere Addition von Punkten auf elliptischen Kurven für die Definition von Einwegfunktionen verwendet. Weitere Anwendungen finden sich bei der Faktorisierung natürlicher Zahlen.

Lösungen der Gleichung $y^{2}=x^{3}+ax+b$ für verschiedene Werte von

. Im Fall $(a,b)=(0,0)$ ist die Kurve singulär und damit keine elliptische Kurve

Werden statt kubischer Polynome solche höheren als vierten Grades betrachtet, erhält man hyperelliptische Kurven (die höheres topologisches Geschlecht haben).

Geschichte

Die Theorie der elliptischen Kurven entwickelte sich zunächst im Kontext der Funktionentheorie. Bei verschiedenen geometrischen oder physikalischen Problemen – so zum Beispiel bei der Bestimmung der Bogenlänge von Ellipsen – treten elliptische Integrale auf. Zu diesen Integralfunktionen konnten Umkehrfunktionen bestimmt werden. Diese meromorphen Funktionen wurden aufgrund dieses Kontextes als elliptische Funktionen bezeichnet (für deren Geschichte siehe dort). Wie weiter unten dargestellt wird, kann man mittels elliptischer Funktionen auf eindeutige Weise jeder elliptischen Kurve über dem Körper der komplexen Zahlen $\mathbb {C}$ einen Torus zuordnen. Auf diese Weise können dann die elliptischen Kurven klassifiziert werden und aufgrund dieses Zusammenhangs haben sie ihren Namen erhalten.

Seit dem Ende des 19. Jahrhunderts stehen arithmetische und zahlentheoretische Fragestellungen im Zentrum der Theorie. Es konnte gezeigt werden, dass elliptische Kurven sinnvoll auf allgemeinen Körpern definiert werden können und es wurde – wie zuvor schon beschrieben – gezeigt, dass eine elliptische Kurve als kommutative Gruppe interpretiert werden kann (was auf Henri Poincaré zurückgeht).

In den 1990er Jahren konnte Andrew Wiles nach Vorarbeiten von Gerhard Frey und anderen mittels der Theorie der elliptischen Kurven die Fermatsche Vermutung aus dem 17. Jahrhundert beweisen.

Affine und projektive Ebene

Der zweidimensionale Raum der -rationalen projektiven Punkte ist definiert als

$\mathbb {P} ^{2}(K)=\{(X,Y,Z)|X,Y,Z\in K{\text{ nicht alle gleich 0}}\}/\!{\sim }$

mit der Äquivalenzrelation

$(X_{1},Y_{1},Z_{1})\sim (X_{2},Y_{2},Z_{2})\Leftrightarrow \exists \lambda \in K^{\ast }:(X_{1},Y_{1},Z_{1})=(\lambda X_{2},\lambda Y_{2},\lambda Z_{2})$ .

Punkte aus $\mathbb{P}^2(K)$ werden üblicherweise als (X:Y:Z) notiert, um sie von Punkten im dreidimensionalen affinen Raum zu unterscheiden.

Die projektive Ebene $\mathbb{P}^2(K)$ kann dargestellt werden als Vereinigung der Menge

$\{(X:Y:1)\mid X,Y\in K\}$

mit der durch Z=0 erzeugten Hyperebene von ${\mathbb P}^{2}(K)$ :

$H=\{(X:Y:0)\mid X,Y\in K{\text{, nicht beide gleich 0}}\}$

Um projektive Kubiken in der affinen Ebene darzustellen, identifiziert man dann für $Z\neq 0$ den projektiven Punkt $(X:Y:Z)=\left({\frac {X}{Z}}:{\frac {Y}{Z}}:1\right)=(x:y:1)$ mit dem affinen Punkt (x,y) .

Im Fall einer elliptischen Kurve hat die (projektive) Polynomgleichung genau eine Lösung mit Z=0 , nämlich den Punkt im Unendlichen ${\mathcal O}=(0:1:0)$ .

Definition

heißt elliptische Kurve über dem Körper , falls eine der folgenden (paarweise äquivalenten) Bedingungen erfüllt ist:

ist eine glatte projektive Kurve über vom Geschlecht 1 mit einem Punkt ${\mathcal O}$ , dessen Koordinaten in liegen.
ist eine glatte projektive Kubik über mit einem Punkt ${\mathcal O}$ , dessen Koordinaten in liegen.
ist eine glatte, durch eine Weierstraß-Gleichung

$Y^{2}Z+a_{1}XYZ+a_{3}YZ^{2}=X^{3}+a_{2}X^{2}Z+a_{4}XZ^{2}+a_{6}Z^{3}$

gegebene projektive Kurve mit Koeffizienten $a_i \in K$ . Schreibt man

$F(X,Y,Z)=Y^{2}Z+a_{1}XYZ+a_{3}YZ^{2}-X^{3}-a_{2}X^{2}Z-a_{4}XZ^{2}-a_{6}Z^{3},$

so ist gerade die Nullstellenmenge des homogenen Polynoms $F\in K[X,Y,Z]$ . (Beachte: Der Punkt $(0:1:0)={\mathcal {O}}$ erfüllt auf jeden Fall die Polynomgleichung, liegt also auf .)

Fasst man als affine Kurve auf, so erhält man eine affine Weierstraß-Gleichung

$y^{2}+a_{1}xy+a_{3}y=x^{3}+a_{2}x^{2}+a_{4}x+a_{6}$

bzw. ein affines Polynom $f(x,y)=y^{2}+a_{1}xy+a_{3}y-x^{3}-a_{2}x^{2}-a_{4}x-a_{6}\in K[x,y]$ . In diesem Fall ist gerade die Menge der (affinen) Punkte, die die Gleichung erfüllen, zusammen mit dem sogenannten „unendlich fernen Punkt“ ${\mathcal O}$ , auch als $\infty$ geschrieben.

Isomorphe elliptische Kurven

Definition

Jede elliptische Kurve wird durch ein projektives Polynom $F(X,Y,Z)\in K[X,Y,Z]$ bzw. durch ein affines Polynom $f(x,y)\in K[x,y]$ beschrieben. Man nennt zwei elliptische Kurven $E_{1}$ und $E_{2}$ isomorph, wenn die Weierstraß-Gleichung von $E_{2}$ aus der von $E_{1}$ durch einen Koordinatenwechsel der Form

$x\mapsto u^{2}x+r$

$y\mapsto u^{3}y+su^{2}x+t$

mit $u,r,s,t\in {\bar {K}},u\neq 0$ entsteht. Die wichtigsten Eigenschaften elliptischer Kurven verändern sich nicht, wenn ein solcher Koordinatenwechsel durchgeführt wird.

Kurze Weierstraß-Gleichung

Ist eine elliptische Kurve über einem Körper mit Charakteristik $\operatorname {char}(K)\not \in \{2,3\}$ durch die Weierstraß-Gleichung

$y^{2}+a_{1}xy+a_{3}y=x^{3}+a_{2}x^{2}+a_{4}x+a_{6}$

gegeben, so existiert ein Koordinatenwechsel, der diese Weierstraß-Gleichung in die Gleichung

$y^{2}=x^{3}+ax+b$

transformiert. Diese nennt man eine kurze Weierstraß-Gleichung. Die durch diese kurze Weierstraß-Gleichung definierte elliptische Kurve ist zur ursprünglichen Kurve isomorph. Häufig geht man daher ohne Einschränkung davon aus, dass eine elliptische Kurve von vorneherein durch eine kurze Weierstraß-Gleichung gegeben ist.

Ein weiteres Resultat der Theorie der Weierstraß-Gleichungen ist, dass eine Gleichung der Form

$y^{2}=x^{3}+ax+b$

genau dann eine glatte Kurve beschreibt, wenn die Diskriminante $\Delta _{E}$ des Polynoms $x^{3}+ax+b$ ,

$\Delta _{E}=-4a^{3}-27b^{2},$

nicht verschwindet. Die Diskriminante ist proportional dem Produkt ${(\lambda _{1}-\lambda _{2})}^{2}\cdot {(\lambda _{1}-\lambda _{3})}^{2}\cdot {(\lambda _{2}-\lambda _{3})}^{2}$ mit den Wurzeln $\lambda _{i}$ des kubischen Polynoms und verschwindet nicht, wenn die Wurzeln paarweise verschieden sind.

Beispiele

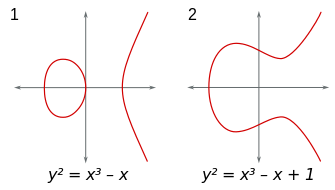
Schaubild der Kurven $y^{2}=x^{3}-x$ und $y^{2}=x^{3}-x+1$

$E_{1}\colon y^{2}=x^{3}-x+1$ und $E_{2}\colon y^{2}=x^{3}+2x-{\sqrt {3}}$ sind elliptische Kurven über $\mathbb {R}$ , da $\Delta _{E_{1}}=4-27=-23\neq 0$ und $\Delta _{E_{2}}=-32-81=-113\neq 0$ sind.
$E\colon y^{2}=x^{3}-x$ ist eine elliptische Kurve sowohl über $\mathbb {Q}$ als auch über $\mathbb {R}$ , da die Diskriminante $\Delta _{E}=4\neq 0$ ist. Über einem Körper mit Charakteristik dagegen ist $\Delta _{E}=0$ und singulär, also keine elliptische Kurve.
$E\colon y^{2}=x^{3}+1$ ist über jedem Körper mit Charakteristik ungleich eine elliptische Kurve, da $\Delta _{E}=-27=-3^{3}\neq 0$ ist.

Über den reellen Zahlen gibt die Diskriminante eine Information über die Form der Kurve in der affinen Ebene. Für $\Delta _{E}>0$ besteht der Graph der elliptischen Kurve aus zwei Komponenten (linke Abbildung), für $\Delta _{E}<0$ hingegen nur aus einer einzigen Komponente (rechte Abbildung).

Gruppenoperation

Elliptische Kurven haben die Besonderheit, dass sie bezüglich der in diesem Abschnitt beschriebenen punktweisen Addition kommutative Gruppen sind. Im ersten Unterabschnitt wird diese Addition geometrisch veranschaulicht, bevor sie dann in den folgenden Abschnitten weiter formalisiert wird.

Geometrische Interpretation

Geometrisch kann die Addition zweier Punkte einer elliptischen Kurve wie folgt beschrieben werden: Der Punkt im Unendlichen ist das neutrale Element $\infty$ . Die Spiegelung eines rationalen Punktes an der -Achse liefert wieder einen rationalen Punkt der Kurve, das Inverse von . Die Gerade durch die rationalen Punkte P,Q schneidet die Kurve in einem dritten Punkt, Spiegelung dieses Punktes an der P+Q .

Im Fall einer Tangente an den Punkt (also des Grenzfalles $Q\to P$ auf der Kurve) erhält man mit dieser Konstruktion (Schnittpunkt der Tangente mit der Kurve, dann Spiegelung) den Punkt P+P . Lassen sich keine entsprechenden Schnittpunkte finden, wird der Punkt im Unendlichen zuhilfe genommen, und man hat z.B. im Fall der Tangente ohne zweiten Schnittpunkt: $P+P=\infty$ . Häufig wird der neutrale Punkt auch mit ${\mathcal O}$ bezeichnet.

Man kann zeigen, dass diese „Addition“ sowohl kommutativ als auch assoziativ ist, sodass sie tatsächlich die Gesetze einer abelschen Gruppe erfüllt. Zum Beweis des Assoziativgesetzes kann dabei der Satz von Cayley-Bacharach eingesetzt werden.

Sei nun ein rationaler Punkt der elliptischen Kurve. Der Punkt P+P wird mit bezeichnet, entsprechend definiert man $kP=P+\dotsb +P$ als k-fache Addition des Punktes . Ist nicht der Punkt ${\mathcal O}$ , kann auf diese Weise jeder rationale Punkt der Kurve erreicht werden (d.h., zu jedem Punkt auf der Kurve existiert eine natürliche Zahl mit $Q=kP$ ), wenn man die richtigen Erzeugenden der Gruppe kennt.

Die Aufgabe, aus gegebenen Punkten P,Q diesen Wert zu ermitteln, wird als Diskreter-Logarithmus-Problem der elliptischen Kurven (kurz ECDLP) bezeichnet. Es wird angenommen, dass das ECDLP (bei geeigneter Kurvenwahl) schwer ist, d.h. nicht effizient gelöst werden kann. Damit bieten sich elliptische Kurven an, um auf ihnen asymmetrische Kryptosysteme zu realisieren (etwa einen Diffie-Hellman-Schlüsselaustausch oder ein Elgamal-Kryptosystem).

Addition zweier verschiedener Punkte

Addition auf der elliptischen Kurve

Seien $P=(x_{P},y_{P})$ und $Q=(x_{Q},y_{Q})$ die Komponenten der Punkte und . Mit wird das Ergebnis der Addition $R:=P+Q:=(x_{R},y_{R})$ bezeichnet. Dieser Punkt hat also die Komponenten $(x_{R},y_{R})$ . Außerdem setze

$s:={\frac {y_{P}-y_{Q}}{x_{P}-x_{Q}}}$ .

Dann ist die Addition $P+Q=(x_{R},y_{R})$ durch

$x_{R}:=s^{2}-x_{P}-x_{Q}$ und
$y_{R}:=-y_{P}+s(x_{P}-x_{R})$

definiert.

Die beiden Punkte und dürfen nicht dieselbe -Koordinate besitzen, da es sonst nicht möglich ist, die Steigung zu berechnen, da dann entweder P=Q oder P=-Q gilt. Bei der Addition $P+(-P)$ erhält man $s={\tfrac {2y_{P}}{0}}$ , wodurch das Ergebnis als $\infty$ (neutrales Element) definiert ist. Dadurch ergibt sich auch, dass und zueinander invers bezüglich der Punktaddition sind. Ist P=Q , handelt es sich um eine Punktverdoppelung.

Verdoppelung eines Punktes

Für die Punktverdoppelung (Addition eines Punktes zu sich selbst) eines Punktes $P=(x_{P},y_{P})$ unterscheidet man zwei Fälle.

Fall 1: $y_{P}\neq 0$

$P+P=R=(x_{R},y_{R})$
$s=(3x_{P}^{2}+a)/(2y_{P})$ . Dabei wird aus der Kurvengleichung ( $y^{2}=x^{3}+ax+b$ ) herangezogen.
$x_{R}=s^{2}-2x_{P}$
$y_{R}=-y_{P}+s(x_{P}-x_{R})$

Der einzige Unterschied zur Addition von zwei verschiedenen Punkten liegt in der Berechnung der Steigung.

Fall 2: $y_{P}=0$

$P+P=\infty$

Wegen $y_{P}=0\Rightarrow P=(-P)$ ist klar erkennbar, dass zu sich selbst invers ist.

Rechenregeln für die „Addition“ von Punkten der Kurve

Analytische Beschreibung über die Koordinaten:

Seien

zwei verschiedene Punkte,
$P=(x_{P},y_{P}),$
$Q=(x_{Q},y_{Q}),$
$x_{P}\neq x_{Q},$
die Addition zweier Punkte und
$\infty$ das neutrale Element (auch Unendlichkeitspunkt genannt).

Es gelten folgende Regeln:

$P+Q=Q+P$
$P+(-P)=\infty$
$P+\infty =P$
$-P=(x_{P},-y_{P})$
$(P+Q)+R=P+(Q+R)$

Skalare Multiplikation eines Punktes

Bei der skalaren Multiplikation $n\cdot P$ handelt es sich lediglich um die wiederholte Addition dieses Punktes.

$n\cdot P=P+\dotsb +P$

Diese Multiplikation kann unter Zuhilfenahme eines angepassten Square-and-Multiply-Verfahrens effizient gelöst werden.

Bei einer elliptischen Kurve über dem endlichen Körper $\mathrm {GF} (q)$ läuft die Punktaddition rechnerisch auf analoge Weise wie bei der Berechnung über $\mathbb {R}$ , jedoch werden die Koordinaten über $\mathrm {GF} (q)$ berechnet.

Elliptische Kurven über den komplexen Zahlen

Interpretiert man wie üblich die komplexen Zahlen als Elemente der gaußschen Zahlenebene, so stellen elliptische Kurven über den komplexen Zahlen eine zweidimensionale Fläche dar, die in den vierdimensionalen ${\mathbb {C}}^{2}$ eingebettet ist. Obwohl sich solche Flächen der Anschauung entziehen, lassen sich dennoch Aussagen über ihre Gestalt treffen, wie zum Beispiel über das Geschlecht der Fläche, in diesem Fall (Torus) vom Geschlecht 1.

Komplexe Tori

Es sei $\Gamma$ ein (vollständiges) Gitter in der komplexen Zahlenebene $\mathbb {C}$ . Die Faktorgruppe ${\mathbb C}/\Gamma$ ist eine eindimensionale abelsche kompakte komplexe Liegruppe, die als reelle Liegruppe isomorph zum Torus $S^{1}\times S^{1}$ ist. Für eine Veranschaulichung kann man Erzeuger v,w von $\Gamma$ wählen; der Quotient ${\mathbb C}/\Gamma$ ergibt sich dann aus der Grundmasche

$\{\lambda v+\mu w\mid 0\leq \lambda ,\ \mu \leq 1\}$ ,

indem man jeweils gegenüberliegende Seiten verklebt.

Bezug zu ebenen Kubiken

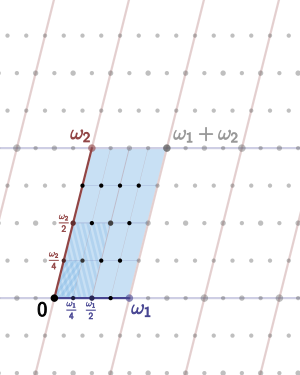
Eine elliptische Kurve ist in der komplexen Ebene durch eine elliptische Funktion definiert über deren Werte in einem Gitter $\Gamma$ , das durch die komplexen Perioden $\omega _{1}$ und $\omega_2$ aufgespannt ist. Eingezeichnet sind auch die 4-Torsionspunkte, die einem Gitter $1/4\ \Gamma$ entsprechen

Ist $\Gamma$ ein Gitter in der komplexen Zahlenebene, so definieren die zugehörige Weierstraßsche ℘-Funktion und ihre Ableitung eine Einbettung

${\mathbb C}/\Gamma \to {\mathbb P}^{2}({\mathbb C}),\quad z\mapsto (1:\wp (z):\wp '(z))$ ,

deren Bild die nichtsinguläre Kubik

$y^{2}=4x^{3}-g_{2}(\Gamma )x-g_{3}(\Gamma )$

ist. Jede nichtsinguläre ebene Kubik ist isomorph zu einer Kubik, die auf diese Weise entsteht.

Das lässt sich durch die Abbildung rechts veranschaulichen. Die elliptische Funktion ist über ihre Weierstraßform in einem Gitter $\Gamma$ der komplexen Ebene definiert, da die Funktion doppeltperiodisch ist (Perioden $\omega _{1}$ , $\omega_2$ , beides komplexe Zahlen, $r\cdot \omega _{1}\neq \omega _{2}$ für ein reelles ). Die Ränder des Gitters werden identifiziert, was geometrisch einen Torus ergibt. Durch die obige Abbildung wird das Gitter in die komplexe projektive Ebene abgebildet und die Addition von Punkten im Quotientenraum (Torus) $\mathbb {C} /\Gamma$ überträgt sich als Gruppenhomomorphismus auf die elliptische Kurve in der projektiven Ebene, was das oben erläuterte „Additionsgesetz“ von Punkten auf der Kurve ergibt.

Punkte von endlicher Ordnung im Gitter heißen Torsionspunkte. Ein Torsionspunkt -ter Ordnung entspricht den Punkten

${\frac {k}{n}}\omega _{1}+{\frac {l}{n}}\omega _{2}$

mit $k,l=0,\dotsc ,n-1$ . In der Abbildung ist der Fall n=4 dargestellt. Bezüglich des oben definierten Additionsgesetzes für Punkte auf elliptischen Kurven gilt für einen -Torsionspunkt $n\cdot P=\infty$ .

Klassifikation

Zwei eindimensionale komplexe Tori ${\mathbb C}/\Gamma _{1}$ und ${\mathbb C}/\Gamma _{2}$ für Gitter $\Gamma _{1},\Gamma _{2}$ sind genau dann isomorph (als komplexe Liegruppen), wenn die beiden Gitter ähnlich sind, d.h. durch eine Drehstreckung auseinander hervorgehen. Jedes Gitter ist zu einem Gitter der Form $\langle 1,\tau \rangle _{{{\mathbb Z}}}$ ähnlich, wobei $\tau$ ein Element der oberen Halbebene $\mathbb {H} =\{z\in \mathbb {C} \mid \operatorname {Im} z>0\}$ ist; sind v,w Erzeuger, so kann $\tau$ als v/w oder w/v gewählt werden. Die verschiedenen Wahlen für Erzeuger entsprechen der Operation der Gruppe ${\mathrm {SL}}_{2}({\mathbb Z})$ auf der oberen Halbebene, die durch

${\begin{pmatrix}a&b\\c&d\end{pmatrix}}\tau ={\frac {a\tau +b}{c\tau +d}}$

gegeben ist (Modulgruppe). Zwei Elemente $\tau _{1},\tau _{2}$ der oberen Halbebene definieren genau dann isomorphe elliptische Kurven ${\mathbb C}/\langle 1,\tau _{1}\rangle$ und ${\mathbb C}/\langle 1,\tau _{2}\rangle$ , wenn $\tau _{1}$ und $\tau _{2}$ in derselben ${\mathrm {SL}}_{2}({\mathbb Z})$ -Bahn liegen; die Menge der Isomorphieklassen elliptischer Kurven entspricht damit dem Bahnenraum

$\mathrm {SL} _{2}(\mathbb {Z} )\backslash \mathbb {H} ;$

dieser Raum wird von der -Funktion, einer Modulfunktion, bijektiv auf $\mathbb {C}$ abgebildet; dabei ist der Wert der -Funktion gleich der -Invarianten der oben angegebenen Kubik.

Elliptische Kurven über den rationalen Zahlen

Die Addition von Punkten elliptischer Kurven ermöglicht es, aus einfachen (geratenen) Lösungen einer kubischen Gleichung weitere Lösungen zu berechnen, die in der Regel weitaus größere Zähler und Nenner haben als die Ausgangslösungen (und deshalb kaum durch systematisches Probieren zu finden wären).

Zum Beispiel für die über $\mathbb {Q}$ definierte elliptische Kurve

$y^{2}=x^{3}-63$

findet man durch Raten die Lösung $P=(x,y)=(4,1)$ und daraus durch Addition auf der elliptischen Kurve die Lösung 2P=(568,-13537) sowie durch weitere Addition auf der elliptischen Kurve dann noch erheblich „größere“ Lösungen. Das ergibt sich aus

für Punkte mit ganzzahligen Koordinaten auf elliptischen Kurven über $\mathbb {Q}$ unter Verwendung der Koordinatenform des Additionsgesetzes (siehe oben). Dabei ist die für ganzzahlige Punkte durch $h(x,y)=\log(\mid x\mid )$ definierte Höhe.

Nach dem Satz von Mordell-Weil ist $E(\mathbb {Q} )$ endlich erzeugt und es gilt $E(\mathbb {Q} )=T\times \mathbb {Z} ^{r}$ , wobei die Torsionsuntergruppen sind und den Rang der elliptischen Kurve bezeichnet. Nach dem Satz von Lutz und Nagell (Élisabeth Lutz, Trygve Nagell, Mitte der 1930er Jahre) gilt für die Punkte P = (x,y) endlicher Ordnung (also die Elemente der Torsionsuntergruppen), dass $x,y\in \mathbb {Z}$ und entweder y=0 (dann ist von der Ordnung 2) oder $y^{2}\mid D$ , das heißt, $y^{2}$ teilt (wobei die Diskriminante ist). Das ermöglicht es, die Torsionsuntergruppen zu berechnen.

Die möglichen Torsionsuntergruppen für elliptische Kurven über den rationalen Zahlen wurden von Barry Mazur klassifiziert in einem schwierigen Beweis (Satz von Mazur (Elliptische Kurven)). Danach kann bei einem Punkt der Ordnung die Zahl einen der Werte 1 bis 10 oder 12 annehmen.

Mit dem Satz von Lutz und Trygvell und dem von Mazur hat man einen Algorithmus zur Bestimmung der Elemente der Torsionsgruppen P=(x,y) einer elliptischen Kurve $y^{2}=f(x)$ über den rationalen Zahlen:

Man finde $y^{2}\mid D$ mit der Diskriminante der Kurve.
Man bestimme die zugehörigen aus der Gleichung der Kurve und hat so die Koordinaten von .
Man berechne $nP$ mit $n=1,\dotsc ,10,12$ (nach dem Satz von Mazur), ist $nP={\mathcal {O}}$ (wobei hier die Notation ${\mathcal O}$ für das neutrale Element verwendet wird), so hat man einen Torsionspunkt. Hat dagegen $nP$ keine ganzzahligen Koordinaten, gehört er nicht zu den Torsionspunkten.

Elliptische Kurven nehmen nach der Vermutung von Mordell (Satz von Faltings, sie entsprechen dort dem Fall des Geschlechts g=1 ) eine Sonderstellung ein, sie können unendlich viele (Rang ungleich null) oder endlich viele rationale Lösungen (Torsionsuntergruppen) haben. Kurven mit g>1 haben dagegen nur endlich viele Lösungen. Im Fall g = 0 gibt es keine oder unendlich viele Lösungen (zum Beispiel beim Kreis unendlich viele pythagoreische Tripel).

Die Theorie elliptischer Kurven über dem Körper der rationalen Zahlen ist ein aktives Forschungsgebiet der Zahlentheorie (arithmetische algebraische Geometrie) mit einigen berühmten offenen Vermutungen wie der Vermutung von Birch und Swinnerton-Dyer, die eine Aussage über das analytische Verhalten die Hasse-Weil-L-Funktion L(E,s) einer elliptischen Kurve macht, in deren Definition die Anzahl der Punkte der Kurve über endlichen Körpern einfließt. Nach der Vermutung in ihrer einfachsten Form ist der Rang der elliptischen Kurve gleich der Ordnung der Nullstelle von L(E,s) bei s=1 .

Elliptische Kurven über endlichen Körpern

Affine Punkte der elliptischen Kurve $y^{2}=x^{3}-x$ über $\mathbf {F} _{61}$

Statt über den rationalen Zahlen kann man elliptische Kurven auch über endlichen Körpern betrachten. In diesem Falle besteht die Ebene, genauer gesagt die projektive Ebene, in der die elliptische Kurve liegt, nur noch aus endlich vielen Punkten. Daher kann auch die elliptische Kurve selbst nur endlich viele Elemente enthalten, was viele Betrachtungen vereinfachen kann. Für die Anzahl der Punkte einer elliptischen Kurve über einem Körper mit Elementen zeigte Helmut Hasse (1936) die Abschätzung (Riemannsche Vermutung)

$|N - (q+1)| \le 2 \sqrt{q}$

und bewies damit eine Vermutung aus der Dissertation von Emil Artin (1924).

Allgemeiner folgt aus den Weil-Vermutungen (einer Reihe von Vermutungen zur Hasse-Weil-Zetafunktion, bewiesen in den 1960er und 1970er Jahren) für die Anzahl $N_{m}$ der Punkte von über einer Körpererweiterung mit $q^{m}$ Elementen die Gleichung

$N_m = q^m + 1 - \alpha^m - \beta^m$ ,

wobei $\alpha$ und $\beta$ die beiden Nullstellen des charakteristischen Polynoms des Frobeniushomomorphismus $\phi_q$ auf der elliptischen Kurve über $\mathbf{F}_{q^m}$ sind. René Schoof (1985) entwickelte den ersten effizienten Algorithmus zur Berechnung von $N_{m}$ . Es folgten Verbesserungen von A. O. L. Atkin (1992) und Noam Elkies (1990).

Elliptische Kurven über endlichen Körpern werden z.B. in der Kryptographie (Elliptische-Kurven-Kryptosystem) eingesetzt.

Die (bisher noch unbewiesene) Vermutung von Birch und Swinnerton-Dyer versucht, Aussagen über gewisse Eigenschaften elliptischer Kurven über den rationalen Zahlen zu erhalten, indem entsprechende Eigenschaften elliptischer Kurven über endlichen Körpern (sogenannte „reduzierte elliptische Kurven“) untersucht werden.

Hasse-Weil-Zetafunktion und L-Funktion für elliptische Kurven

Die elliptische Kurve über $\mathbb {Q}$ sei durch die Gleichung

$y^{2}+a_{1}xy+a_{3}y=x^{3}+a_{2}x^{2}+a_{4}x+a_{6}$

mit ganzzahligen Koeffizienten $a_{i}$ gegeben. Die Reduktion der Koeffizienten modulo einer Primzahl definiert eine elliptische Kurve über dem endlichen Körper $\mathbb{F}_p$ (mit Ausnahme einer endlichen Menge von Primzahlen , für welche die reduzierte Kurve Singularitäten aufweist und deshalb nicht elliptisch ist; in diesem Fall sagt man, habe schlechte Reduktion bei ).

Die Zetafunktion einer elliptischen Kurve über einem endlichen Körper ist die formale Potenzreihe

$Z(E({\mathbb {F}}_{p}))=\exp \left(\sum {\mathrm {card}}\left[E({{\mathbb F}}_{{p^{n}}})\right]{\frac {T^{n}}{n}}\right).$

Sie ist eine rationale Funktion der Form

$Z(E({\mathbb {F}}_{p}))={\frac {1-a_{p}T+pT^{2}}{(1-T)(1-pT)}}.$

(Diese Gleichung definiert den Koeffizienten $a_{p}$ , falls gute Reduktion bei hat, die Definition im Fall schlechter Reduktion ist eine andere.)

Die -Funktion von über $\mathbb {Q}$ speichert diese Information für alle Primzahlen . Sie ist definiert durch

$L(E(\mathbb {Q} ),s)=\prod _{p}\left(1-a_{p}p^{-s}+\varepsilon (p)p^{1-2s}\right)^{-1}$

mit $\varepsilon (p)=1$ , falls gute Reduktion bei hat, und $\varepsilon (p)=0$ sonst.

Das Produkt konvergiert für $\textstyle \Re (s)\;>\;{\frac {3}{2}}$ . Helmut Hasse vermutete, dass die -Funktion eine analytische Fortsetzung auf die gesamte komplexe Ebene besitzt und eine Funktionalgleichung mit einem Zusammenhang zwischen L(E,s) und L(E,2-s) erfüllt. Hasses Vermutung wurde 1999 als Konsequenz des Beweises des Modularitätssatzes bewiesen. Dieser besagt, dass jede elliptische Kurve über $\mathbb {Q}$ eine modulare Kurve ist, und für die -Funktionen modularer Kurven ist die analytische Fortsetzbarkeit bekannt.

Anwendung in der Kryptographie

Der US-Auslandsgeheimdienst NSA empfahl im Januar 2009, Verschlüsselung im Internet bis 2020 von RSA auf ECC (Elliptic Curve Cryptography) umzustellen.

ECC ist ein Public-Key-Kryptosystem (oder asymmetrisches Kryptosystem), bei dem im Gegensatz zu einem symmetrischen Kryptosystem die kommunizierenden Parteien keinen gemeinsamen geheimen Schlüssel kennen müssen. Asymmetrische Kryptosysteme allgemein arbeiten mit Falltürfunktionen, also Funktionen, die leicht zu berechnen, aber ohne ein Geheimnis (die „Falltür“) praktisch unmöglich zu invertieren sind.

Die Verschlüsselung mittels elliptischer Kurven funktioniert im Prinzip so, dass man die Elemente der zu verschlüsselnden Nachricht (d.h. die einzelnen Bits) auf irgendeine Weise den Punkten einer (festen) elliptischen Kurve zuordnet und dann die Verschlüsselungsfunktion $P\mapsto nP$ mit einer (festen) natürlichen Zahl n>1 anwendet. Damit dieses Verfahren sicher ist, muss die Entschlüsselungsfunktion $nP\mapsto P$ schwer zu berechnen sein.

Da das Problem des diskreten Logarithmus in elliptischen Kurven (ECDLP) deutlich schwerer ist als die Berechnung des diskreten Logarithmus in endlichen Körpern oder die Faktorisierung ganzer Zahlen, kommen Kryptosysteme, die auf elliptischen Kurven beruhen – bei vergleichbarer Sicherheit – mit erheblich kürzeren Schlüsseln aus als die herkömmlichen asymmetrischen Kryptoverfahren, wie z.B. das RSA-Kryptosystem. Die derzeit schnellsten Algorithmen sind der Babystep-Giantstep-Algorithmus und die Pollard-Rho-Methode, deren Laufzeit bei $O\left(2^{n/2}\right)$ liegt, wobei die Bitlänge der Größe des zugrundeliegenden Körpers ist.

Basierend auf einem Artikel in:

Wikipedia.de