Abelsche Gruppe
Eine abelsche Gruppe ist eine Gruppe, für die zusätzlich das Kommutativgesetz gilt.
Der mathematische Begriff abelsche Gruppe, auch kommutative
Gruppe genannt, verallgemeinert das Rechnen mit Zahlen. Addition rationaler
Zahlen und die Multiplikation rationaler Zahlen
erfüllen eine Reihe gemeinsamer Gesetze. Diese Regeln kommen oft in Geometrie
und Algebra vor. So zum Beispiel bei Verschiebungen, Drehungen der Ebene um
einen Punkt, Addition von Funktionen. Ornamente in Kunst und Natur zeichnen die
Spuren abelscher Gruppen. Deswegen wird von der speziellen Bedeutung des
Additionszeichens
und des Multiplikationszeichens
abstrahiert und der Begriff der kommutativen oder abelschen Gruppe geschaffen.
Der Name ist zu Ehren des norwegischen Mathematikers Niels Henrik Abel
gewählt worden.
Definition
Sei
eine Menge.
Jedem Paar
sei genau ein Element
zugeordnet. Das Paar
heißt abelsche Gruppe, wenn die Verknüpfung
die folgenden Gesetze erfüllt:
- Assoziativgesetz:
Für alle
gilt:
.
- Kommutativgesetz:
Für alle
gilt:
.
- Neutrales
Element: Es gibt ein Element
, so dass für alle
gilt:
.
- Inverses
Element: Zu jedem
gibt es ein
mit
.
Eine Gruppe
heißt nichtabelsch, wenn in ihr mindestens ein Paar
existiert mit
.
Erläuterungen
- Wird bei den Axiomen das Kommutativgesetz weggelassen, so ergibt sich eine Gruppe. Eine abelsche Gruppe ist daher nichts anderes als eine Gruppe, für die zusätzlich das Kommutativgesetz gilt.
- Das neutrale Element und das inverse Element eines jeden Gruppenelementes sind eindeutig bestimmt, wie sich aus den Axiomen zeigen lässt.
- Meist wird eine abelsche Gruppe additiv mit dem Verknüpfungszeichen
geschrieben und dann ein Modul genannt. In diesem Falle heißen
die Summe von
und
, das neutrale Element Nullelement oder einfach Null und wird
geschrieben. Das Inverse von
wird dann als dessen Entgegengesetztes mit
bezeichnet.
- Eine kommutative Gruppe kann auch multiplikativ mit dem
Verknüpfungszeichen
geschrieben werden. Dann heißt
oder einfach
das Produkt von
und
. In diesem Falle heißt das neutrale Element Einselement oder einfach Eins und wird
geschrieben. Das Inverse von
bezeichnet man nun mit
.
- In einem Modul wird die Differenz zweier Elemente erklärt als
. Es gelten dann die Regeln:
. Wird die abelsche Gruppe multiplikativ geschrieben, so definiert man entsprechend den Quotienten
.
Beispiele
ist die wichtigste abelsche Gruppe. Dabei ist
die Menge der ganzen Zahlen und
die gewöhnliche Addition.
ist eine abelsche Gruppe. Dabei ist
die Menge der rationalen Zahlen ohne die
und
ist die gewöhnliche Multiplikation.
- Die Menge der endlichen Dezimalzahlen sind bezüglich der Multiplikation
keine abelsche Gruppe. Zum Beispiel hat die Zahl
kein Inverses bezüglich der Multiplikation.
lässt sich nicht als endlicher Dezimalbruch schreiben. Bezüglich der normalen Addition bilden die endlichen Dezimalbrüche eine abelsche Gruppe.
- Die Menge der Verschiebungen
in der euklidischen Ebene bilden eine abelsche Gruppe. Die Verknüpfung ist die
Hintereinanderausführung der Verschiebungen.
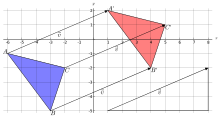 Ein Dreieck wird um den Verschiebungsvektor
Ein Dreieck wird um den Verschiebungsvektorverschoben
- Die Menge der Drehungen in einer Ebene um einen Punkt bilden eine abelsche Gruppe. Die Verknüpfung ist die Hintereinanderausführung der Drehungen.
- Die Menge der Drehstreckungen in einer Ebene bilden eine abelsche Gruppe.
- Von genügend kleinen Gruppen lässt sich die Verknüpfungstafel
aufschreiben.
. Ist es die Tafel einer abelschen Gruppe, so ist die Tafel symmetrisch zur Hauptdiagonale. Diese Tafel ergibt sich beispielsweise, wenn man die Drehungen eines gleichseitigen Dreiecks um den Schwerpunkt betrachtet, die das Dreieck in sich überführen.
ist die Drehung um
,
ist die Drehung um
und
ist die Drehung um
.
- Sind
abelsche Gruppen, so wird
zu einer abelschen Gruppe durch
.
- Ist
eine Menge und
eine abelsche Gruppe, so ist
eine Gruppe, wenn definiert wird:
. Es heißt
die
te Komponente von
. Oft wird
als Vektor geschrieben der Form
. Dabei ist
. Ist
, so ist
die Menge der Folgen, wobei die Folgenglieder Elemente aus
sind. Ist
, so ist
.
- Die reellen Zahlen bilden mit der Addition eine abelsche Gruppe; ohne die Null bilden sie mit der Multiplikation eine abelsche Gruppe.
- Allgemeiner liefert jeder Körper
in derselben Weise zwei abelsche Gruppen
und
.
- Hingegen ist die Gruppe
der invertierbaren
-Matrizen über einem Körper
für
ein Beispiel für eine nichtabelsche Gruppe. Die kleinste nichtabelsche Gruppe ist übrigens die symmetrische Gruppe S3 mit sechs Elementen.
Untergruppen
Eine nicht leere Teilmenge
der abelschen Gruppe
heißt Untergruppe, wenn sie bezüglich der Gruppenoperation selber eine
Gruppe ist. Dies ist genau dann der Fall, wenn für alle
gilt:
In diesem Artikel wird die folgende Bezeichnung gewählt:
.
ist Untergruppe von
.
- Der Durchschnitt von Untergruppen ist eine Untergruppe.
- Jede Teilmenge
ist enthalten in einer kleinsten Untergruppe, die
enthält. Diese Untergruppe heißt die von
erzeugte Untergruppe von
. Sie wird mit
bezeichnet.
- Sind
Untergruppen von
, so ist die Menge
eine Untergruppe von
. Allgemeiner: Ist
eine Familie von Untergruppen, so ist
eine Untergruppe von
. Sie heißt die Summe der Untergruppen .
- Ist
, so ist die von
erzeugte Untergruppe
. Ist
so heißt
ein Erzeugendensystem von
.
- Eine abelsche Gruppe
heißt endlich erzeugt , wenn es eine endliche Teilmenge
gibt, so dass
gilt. Ist
von einem Element
erzeugt, so heißt
zyklisch. Es wird
geschrieben.
- Jede Untergruppe von
ist zyklisch.
- Das heißt beispielsweise: Die Summe zweier zyklischer Untergruppen von
ist wieder zyklisch. Es gilt
. Dabei ist
der größte gemeinsamer Teiler von
. z.B.
.
- Sind
Untergruppen von
, dann ist
. Dabei ist
das kleinste gemeinsame Vielfache von
. Zum Beispiel
.
ist nicht endlich erzeugt. Genauer: Ist
ein Erzeugendensystem von
und ist
, so ist auch noch
ein Erzeugendensystem.
- Jede Untergruppe von
- Einige Gruppen in Kunst und Natur
-
 Fra Giovanni da Verona malte dieses Bild als Intarsie in der Sacrestia die Santa Maria in Organo. Es veranschaulicht eine zyklische Gruppe der Ordnung 8 samt einer Untergruppe der Ordnung 4.
Fra Giovanni da Verona malte dieses Bild als Intarsie in der Sacrestia die Santa Maria in Organo. Es veranschaulicht eine zyklische Gruppe der Ordnung 8 samt einer Untergruppe der Ordnung 4. -
 Der Entwurf von Bramante zum Petersdom. Unter anderem ist es eine Drehgruppe der Ordnung 4. Tatsächlich ist mathematisch noch mehr darin versteckt. Es ist ein Fraktal.
Der Entwurf von Bramante zum Petersdom. Unter anderem ist es eine Drehgruppe der Ordnung 4. Tatsächlich ist mathematisch noch mehr darin versteckt. Es ist ein Fraktal. -
 Die Blüte zeigt die Symmetrie der Drehgruppe der Ordnung 5. Auch das entstehende Pentagramm ist deutlich zu erkennen.
Die Blüte zeigt die Symmetrie der Drehgruppe der Ordnung 5. Auch das entstehende Pentagramm ist deutlich zu erkennen.
Faktorgruppen
Ist
eine Untergruppe, so definiert
eine Äquivalenzrelation. Sind
und sind
so ist
.
Die Äquivalenzrelation heißt verträglich mit der Addition. Sei
Menge der Äquivalenzklassen. Auf
wird eine Addition erklärt.
.
Wollen wir tatsächlich in
rechnen, so genügt es sich auf ein Repräsentantensystem von
zu beschränken. Denn jede Äquivalenzklasse ist durch ein Element aus der
Äquivalenzklasse eindeutig bestimmt. Es ist
.
- Ist
eine Untergruppe von
, so ist
zyklisch. Das heißt es gibt ein
mit
. Ist
, so gibt es einen positiven Repräsentanten in der Äquivalenzklasse von
. Es ist daher keine Einschränkung, wenn wir
voraussetzen. Wir erhalten einen Repräsentanten von
durch Teilen mit Rest. Es ist für zwei positive
genau dann, wenn sie beim Teilen durch
den gleichen Rest lassen. Es ist dann
ein Repräsentantensystem von
. Bezeichnet
der Rest, der beim Teilen von
durch
sich ergibt, so entspricht dem Rechnen in
folgende 'Addition':
für
. Den Index
beim
Zeichen lässt man weg. So ergibt in
zum Beispiel
.
ist eine Untergruppe von
. Ein Repräsentantensystem von
ist das rechts offene Einheitsintervall
. In diesem Repräsentantesystem rechnet man folgendermaßen:
. Dabei ist
größte ganze Zahl
. Es ist daher für
:
- Die besonderen Eigenschaften der Untergruppe
von
kommen etwas weiter unten zur Sprache.
Homomorphismen
Definition
Sind
abelsche Gruppen, so heißt eine Abbildung
Homomorphismus , wenn für alle
gilt:
.
Beispiele für Homomorphismen
- Die Identität und die Nullabbildung
sind stets Homomorphismen. Zu jeder abelschen Gruppe
gibt es genau einen Morphismus
. Genauso gibt es genau einen Homomorphismus
.
- Ist
eine Untergruppe von
, so ist die Inklusionsabbildung ein Homomorphismus.
- Die Abbildung
ist ein Homomorphismus. Allgemein: Ist
so ist die Multiplikation mit
, also die Abbildung
, ein Homomorphismus. Dies ist äquivalent zum Distributivgesetz, welches besagt: Für alle
gilt:
. Die Multiplikationen sind auch die einzigen Homomorphismen
das heißt: Ist
ein Homomorphismus, so gibt es ein
mit
für alle
.
- Ist
, so ist die Abbildung
ein Homomorphismus, von der additiven Gruppe
in die multiplikative Gruppe
.
- Die natürliche Exponentialfunktion:
ist ein Homomorphismus abelscher Gruppen. Sie bildet die additive Gruppe
bijektiv in die multiplikative Gruppe
ab. Die Umkehrabbildung ist der natürliche natürlicher Logarithmus.
- Die Verkettung von Homomorphismen ist ein Homomorphismus. Die Klasse der
abelschen Gruppen, zusammen mit den Homomorphismen bilden eine Kategorie
(Mathematik)
. Diese ist der Prototyp einer abelschen Kategorie.
Universelle Eigenschaft der ganzen Zahlen
- Zu jeder Gruppe
und jedem
gibt es genau einen Homomorphismus
mit
. Es ist dann
, und
. Allgemein ist
.
Es ist
eine freie
abelsche Gruppe mit Basis
.
- Es liegt nahe für
und
zu definieren:
. Es gilt dann:
. (Achtung! Es kann verwirren, dass auf beiden Seiten der Gleichung das gleiche Zeichen
verwendet wird. Auf der linken Seite der Gleichung steht das neutrale Element in
. Auf der rechten Seite der Gleichung steht das neutrale Element in
. Beide Male sind die verschiedenen neutralen Elemente mit
geschrieben.)
- Für alle
ist
.
- Für alle
und alle
ist
.
- Für alle
und alle
ist
.
- Für alle
und alle
ist
.
- Jeder Modul wird auf diese Weise zu einem
Modul. Ist
ein Homomorphismus, so ist für alle
:
.
- Es lohnt sich die vorletzte Aussage für eine Gruppe
zu übersetzen, die multiplikativ geschrieben wird. In diesem Falle ist das Neutralelement in
die
. Zu jedem beliebigen
gibt es genau einen Homomorphismus
mit
. Es ist
. Allgemein ist
. Die obigen Gesetze besagen dann:
- Für alle
ist
.
- Für alle
ist
.
- Für alle
ist
.
- Für alle
ist
. Wird für
die Menge der rationalen oder reellen Zahlen
eingesetzt, so ergeben sich die aus der Schule bekannten Gesetze für das Rechnen mit Exponenten.
Eigenschaften von Homomorphismen
Ist
ein Homomorphismus, und sind
beziehungsweise
Untergruppen, so sind
und
Untergruppen. Insbesondere sind
und
Untergruppen. Hieraus folgt:
- Ist
eine Gruppe und
eine natürliche Zahl, so ist
und
Untergruppen von
. Dies gilt, da die Multiplikation mit
ein Homomorphismus ist.
ist Untergruppe von
. Dies ist die Torisonsuntergruppe von
. Ist
, so heißt
torsionsfrei. Für jede Gruppe ist
torionsfrei. Die Torsionsuntergruppe von
ist
.
- Ist
ein Homomorphismus und ist
von
Elementen erzeugt und ist
von
Elementen erzeugt, so ist
von
Elementen erzeugt.
- Jede Untergruppe von
ist von maximal
Elementen erzeugt.
Injektive Homomorphismen
- Ist
ein bijektiver Homomorphismus, so ist auch die Umkehrabbildung
ein Homomorphismus. In diesem Fall heißt
Isomorphismus. Gibt es einen Isomorphismus zwischen
und
so heißen
isomorph.
- Ist
ein Homomorphismus, so sind folgende Aussagen äquivalent. In diesem Fall heißt
Monomorphismus.
ist als Abbildung injektiv.
.
- Für alle abelschen Gruppen
und alle Homomorphismen
mit
ist
. Es ist
links kürzbar.
- Die Verkettung von Monomorphismen ist ein Monomorphismus. Das heißt
genauer: Sind
Monomorphismen, so ist
ein Monomorphismus.
Surjektive Homomorphismen
Ist
ein Homomorphismus, so sind die folgenden Aussagen äquivalent. Dann heißt
Epimorphismus.
ist als Abbildung surjektiv.
.
- Für alle Gruppen
und alle
gilt: Ist
, so ist
. Es ist
auf der rechten Seite kürzbar.
- Ist
eine Untergruppe, so ist die Abbildung
ein Epimorphismus.
- Die Verkettung von Epimorphsmen ist ein Epimorphismus. Das heißt genauer:
Sind
und
Epimorphismen, so ist
ein Epimorphismus. Er heißt kanonischer Epimorphismus.
- Sind
und
Homomorphismen und ist
ein Epimorphismus, so ist
ein Epimorphismus.
Isomorphismus, Isomorphiesätze
Ein bijektiver Homomorphismus
heißt Isomorphismus. Dies ist genau dann der Fall, wenn er monomorph und
epimorph ist. Es gelten die folgenden Sätze.
- Homomorphiesatz: Sei
ein Homomorphismus.
der kanonische Epimorphismus. Dann ist
ein Monomorphismus mit
. Insbesondere ist
Es ist folgendes Diagramm kommutativ.
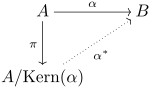 Homomorphiesatz
Homomorphiesatz
Der Homomorphiesatz gilt allgemein für Gruppen.
- Erster Isomorphiesatz: Seien
Untergruppen von
. Dann gilt:
.
- Zweiter Isomorphiesatz: Seien
Untergruppen. Dann gilt :
.
Der Funktor Hom(A, –)
- Sind
Gruppen, so ist die Menge
eine Gruppe. Die Addition ist erklärt durch:
.
- Es ist
für jede endlich erzeugte Gruppe
.
- Ist der größte gemeinsame Teiler zwei Zahlen
gleich
, so ist
.
- Für alle abelschen Gruppen
ist
. Diese Isomorphie ist ein funktorieller Isomorphismus. Genauer wird dies weiter unten ausgeführt.
- Es ist
- Ist
ein Homomorphismus, so ist die Zuordnung
ein Homomorphismus. Für
gilt:
. Ist
die Identität auf
, so ist
die Identität auf
. Ist
ein Isomorphismus, so ist
ein Isomorphismus. Wird
- Jeder abelschen Gruppe
die abelsche Gruppe
und
- jedem Homomorphismus
der Homomorphismus
zugeordnet, so erhält man den Funktor
von der Kategorie der abelschen Gruppen
in die Kategorie
.
- Jeder abelschen Gruppe
- Die letzte Aussage wirft ein Licht auf die universelle Eigenschaft von
. Da es zu jedem
einen eindeutig bestimmten Homomorphismus
mit
gibt, ist die Zuordnung
eine Funktion. Es gilt genauer: Die Familie der Abbildungen:
hat die folgende Eigenschaft: Für alle
und alle Homomorphismen
ist
. Außerdem ist für alle
die Abbildung
ein Isomorphismus. Die Umkehrabbildung ist:
. Das heißt folgendes Diagramm ist kommutativ für alle
SPAN> und alle
mit Isomorphismen
.
Das heißt unter anderem.png)
ist Monomorphismus oder Epimorphismus genau dann, wenn
dies ist.
- Hom(G,-) und exakte Folgen: Ist
eine exakte Folge exakte Folge abelscher Gruppen, so ist für jede Gruppe
die induzierte Folge
exakt. Dabei ist
. Der Funktor
heißt links exakt. Ist
ein Epimorphismus, so ist normalerweise
kein Epimorphismus.
- Für
gelten die folgenden Gesetze.
- Für alle
ist
und
.
- Für alle
ist
und
.
- Für alle
ist
.
ist ein unitärer Ring.
- Für alle
Verallgemeinerungen, Weiterführendes
Die Theorie der abelschen Gruppen ist reichhaltig. Hier sei auf einige grundlegende Begriffe hingewiesen. Manchmal gibt es zu einem Teilaspekt einen Eintrag in der Wikipedia. Meist nicht.
- Jeder Modul ist ein Modul über dem Ring
(siehe oben). Wird
durch einen beliebigen Ring
ersetzt, erhalten wir einen
-Modul. Sätze über abelsche Gruppen können so oft auf Moduln über Hauptidealbereichen übertragen werden. Ein Beispiel ist die Klassifikation endlich erzeugter abelscher Gruppen (siehe unten).
- Torsionsgruppen:
Ein
heißt Torsionselement, wenn es eine natürliche Zahl gibt, so dass
. Die Menge aller Torsionselement in einer Gruppe
bilden eine Untergruppe.
ist die Torsionsuntergruppe von
.
- Direkte
Summen abelscher Gruppen: Für den Fall zweier Untergruppen
sei der Begriff hier erklärt. Ist
und
, so heißt
direkte Summe von
.
- Direktes Produkt.
- freie
abelsche Gruppe: Manche abelschen Gruppen haben so etwas wie eine Basis in
einem Vektorraum. In der Theorie der
-Moduln spielen die freien Moduln eine große Rolle.
- Teilbare abelsche Gruppe
- endlich erzeugte abelsche Gruppe. Ihre Struktur ist so ziemlich geklärt. Sie sind direkte Summe von unzerlegbaren zyklischen Gruppen.
- Für beliebige abelsche Gruppen kann man analog zum Begriff der Dimension
eines Vektorraums jeder
abelschen Gruppe ihren Rang
zuordnen. Er ist definiert als die größte Mächtigkeit
einer
-linear unabhängigen Teilmenge. Die ganzen Zahlen und die rationalen Zahlen
haben Rang 1, so wie jede Untergruppe von
. Die abelschen Gruppen vom Rang 1 sind gut verstanden, dagegen sind für höhere Ränge noch viele Fragen offen. Abelsche Gruppen mit unendlichem Rang können extrem komplex sein und ihre offenen Fragen sind oft eng verbunden mit Fragen der Mengenlehre.
- Viele abelsche Gruppen haben eine natürliche Topologie, durch die sie zu topologischen Gruppen werden.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 21.06. 2021