Enzymkinetik
Die Enzymkinetik ist ein Teilgebiet der biophysikalischen Chemie. Sie beschreibt, wie schnell enzymkatalysierte chemische Reaktionen verlaufen. Die Enzymkinetik findet breite Anwendung in Biologie und Medizin, da auch biologische Substrate (Reaktionspartner) – darunter solche, die im Menschen auftreten – untersucht werden. Ein Hauptziel der Enzymkinetik ist die Beschreibung der Konzentrationsabhängigkeit der Reaktionsgeschwindigkeit mit geeigneten Formeln, sowie die Bestimmung der dazugehörigen Parameter für ein bestimmtes Protein (Enzymaktivität und katalytische Effizienz). Da Enzyme dazu dienen, Reaktionen zu beschleunigen und zu lenken, ist die enzymkinetische Analyse zum Verständnis von Enzymfunktionen unerlässlich.
Theorie für Enzyme mit einer Substratbindungsstelle
Der erste, der den Zusammenhang zwischen Substrat-Konzentration und Umsatzgeschwindigkeit eines Enzymes
beschrieb,
war der französische Physikochemiker Victor Henri 1902.
Allerdings war die Bedeutung der Wasserstoffionenkonzentration für enzymatische Reaktionen damals noch nicht bekannt, erst nachdem Sørensen 1909 den pH-Wert
definiert und die Pufferung eingeführt hatte, konnten der Deutsche Leonor Michaelis und seine kanadische Post-Doktorandin
Maud Menten 1913 die Ergebnisse Henris experimentell bestätigen.
Die Henri-Michaelis-Menten-Gleichung wurde 1925 von G. E. Briggs und J. B. S. Haldane verallgemeinert
(Michaelis-Menten-Theorie).
Henris Schlüsselidee war, die enzymatische Reaktion in zwei Phasen zu zerlegen, die Bindung des Substrates S an das Enzym E und die Umsetzung des resultierenden Enzym-Substrat-Komplexes ES in Enzym und Produkt P:
(1)
Hierbei sind Geschwindigkeitskonstanten, die bei der kinetischen Herleitung des
Massenwirkungsgesetzes (MWG) verwendet werden.
Zur Beschreibung eines Reaktionsgleichgewichts der Bindungsreaktion hat die Gleichheit der Geschwindigkeiten von Hin- und Rückreaktion die Form:
wobei die Konzentration der Substanz
bezeichnet.
Durch die angegebenen mathematischen Operationen entsteht für die Bindungsreaktion die eingeführte Formulierung des MWGs:
(2)
Da die (nach Standard im Zähler notierten) Reaktionsprodukte aus einer Dissoziation des Enzym-Substrat-Komplexes hervorgehen, wird die Gleichgewichtskonstante
als Dissoziationskonstante bezeichnet.
Wie aus Gleichung (2) hervorgeht, hat die Dimension einer Konzentration. Für
die Substratkonzentration
ist die Hälfte aller Enzymmoleküle an Substrat gebunden, die andere Hälfte ist frei; dies wird als
Halbsättigung des Enzyms bezeichnet. (Die Weiterreaktion
bleibt zunächst außer Betracht.)
| Rechnung hierzu |
Einsetzen von
|
ist umgekehrt proportional zur
Affinität des Enzymes für das Substrat: Je besser das Enzym das Substrat
bindet, umso niedriger ist die für eine Halbsättigung des Enzyms erforderliche Substratkonzentration.
Zur Beschreibung eines Reaktionsgleichgewichts der Reaktion (1) insgesamt hat die Gleichheit der Geschwindigkeiten von Hin- und Rückreaktion die Form:
hierbei ist
die Geschwindigkeitskonstante der (als nicht umkehrbar vorausgesetzten) Reaktion
.
Durch die angegebenen mathematischen Operationen entsteht für die Reaktion (1) die eingeführte Formulierung des MWGs:
(3)
heißt Michaelis-Menten-Konstante. Zur Beschreibung der Reaktionsgeschwindigkeit
der betrachteten Katalyse wird (für entsprechend geeignete Fälle) weiter vorausgesetzt:
- Die Konzentration
des insgesamt vorhandenen Enzyms ändert sich nicht und ist die Summe aus den Konzentrationen substratgebundenen und freien Enzyms, also
.
- Die katalysierte Reaktion ist erster Ordnung, so dass ihre Geschwindigkeit zur Konzentration
des Enzym-Substrat-Komplexes proportional ist, also
.
- Eine maximale Reaktionsgeschwindigkeit
wird als Rechengröße eingeführt. Diese entspricht dem fiktiven Fall, dass sämtliches vorhandenes Enzym als Enzym-Substrat-Komplex vorliegt, also
.
Durch Einführung dieser Bedingungen lässt sich (3) in die Michaelis-Menten-Gleichung umformen, die
in Abhängigkeit von der Substratkonzentration
darstellt:
| Umformung |
|
|
Der Graph dieser Gleichung ist Teil einer
Hyperbel, die sich für zunehmende
der
waagerechten Asymptote
nähert.
| Rechnung zur Klassifikation des Graphen als Teil einer Hyperbel; Betrachtung der Asymptoten |
|
A. Da eine Hyperbel mit der waagerechten Asymptote
da B. Die beiden zuerst genannten Kongruenzabbildungen ändern nichts an der waagerechten Asymptote der Hyperbel, die letztgenannte verschiebt sie um
Die zuerst genannte Kongruenzabbildungen verschiebt die senkrechte Asymptote der Hyperbel um
|
Wie aus Gleichung (3) hervorgeht, hat auch die Dimension einer Konzentration.
Für die Substratkonzentration
ist
.
| Rechnung hierzu |
|
Einsetzen von
|
Zur Bestimmung von und
aus Messreihen von
und
dienen computergestützte Verfahren wie die nichtlineare Regressionsanalyse
(Simplex- oder
Levenberg-Marquardt-Verfahren).
Graphische Extrapolationsverfahren (Linearisierungen) wie etwa die
doppelt-reziproke Auftragung nach Lineweaver und Burk sollten dafür nicht verwendet werden,
da sie zu ungenau sind. Sie eignet sich jedoch sehr gut zur Präsentation der Ergebnisse enzymkinetischer Versuche.
Theorie für Enzyme mit mehreren Substratbindungsstellen
Die Hill-Gleichung und ihre Herleitung aus dem Massenwirkungsgesetz
Die Hill-Gleichung wurde ursprünglich von Archibald Vivian Hill eingeführt, um die Sauerstoffbindung an Hämoglobin in Abhängigkeit von verschiedenen Sauerstoffkonzentrationen mathematisch zu beschreiben. Die hier beschriebene Hill-Gleichung ist eine andere als die Hill-Gleichung zur Beschreibung der Muskelkontraktion, an deren Erstellung der gleiche Autor beteiligt war.
Obwohl die Bindung von Sauerstoff an Hämoglobin kein katalytischer Vorgang ist, lässt sich mit einer Hill-Gleichung auch die Kinetik enzymatischer
Katalysen beschreiben, insbesondere auch solcher, deren Kinetik sich nicht mit einer Michaelis-Menten-Gleichung beschreiben lässt. Hier folgt eine
Herleitung der Hill-Gleichung aus dem Massenwirkungsgesetz, die die Analogie zur Herleitung der Michaelis-Menten-Gleichung hervorhebt. Entsprechend bedeutet
die Variable
die Anzahl der Bindungsstellen, die ein Molekül Enzym für je ein Molekül Substrat bereithält, und ist damit eine positive
natürliche Zahl. Die experimentell gefundenen Werte von
weichen hiervon ab
(s.u. "Der empirische Hill-Koeffizienten
als Maß der
Kooperativität von Enzymen").
Die Bindung von
Molekülen Substrat an ein Enzym lässt sich modellieren mit:
(1')
Wie in Gleichung (1) sind Geschwindigkeitskonstanten, die bei der kinetischen Herleitung des
Massenwirkungsgesetzes (MWG) verwendet werden. Zur Beschreibung
eines Reaktionsgleichgewichts der Bindungsreaktion hat die Gleichheit der Geschwindigkeiten von Hin- und Rückreaktion die Form:
hierbei ist die Konzentration freien Enzyms,
die Substratkonzentration,
die Konzentration der Enzym-Substrat-Komplexe mit
Molekülen Substrat.
Der Exponent
heißt Hill-Koeffizient. Durch die angegebenen mathematischen Operationen entsteht für die Bindungsreaktion die eingeführte Formulierung des MWGs:
(2')
Analog der Dissoziationskonstante in Gleichung (2) heißt
scheinbare Dissoziationskonstante. Das Adjektiv "scheinbar" trägt der Tatsache Rechnung, dass die experimentell
gemessenen Werte für
von den nach diesem Modell zu erwartenden abweichen.
Wie aus Gleichung (2') hervorgeht, hat die (neu einzuführende) Konstante
(3')
die Dimension einer Konzentration. Für die Substratkonzentration ist die Hälfte aller Enzymmoleküle an Substrat gebunden,
die andere Hälfte ist frei; dies wird als Halbsättigung des Enzyms bezeichnet.
| Rechnung |
|
Gleichsetzen der Gleichungen (2') und (3') ergibt: Einsetzen von
|
wird daher als Halbsättigungskonstante bezeichnet und auch
(für „50%“) geschrieben.
ist (wie die Konstante
der Michaelis-Menten-Gleichung) umgekehrt proportional zur
Affinität des Enzymes für das Substrat:
Je besser das Enzym das Substrat bindet, umso niedriger ist die für eine Halbsättigung des Enzyms erforderliche Substratkonzentration.
Wenn weiter vorausgesetzt wird,
- dass sich die Konzentration
des insgesamt vorhandenen Enzyms nicht ändert und die Summe aus den Konzentrationen substratgebundenen und freien Enzyms ist, also
,
dann ist der Anteil substratgebundenen Enzyms an insgesamt vorhandenem mit Gleichung (2'):
Hill-Gleichung
| Rechnung |
|
|
Um mit der Hill-Gleichung die Reaktionsgeschwindigkeit der Katalyse durch ein Enzym mit mehreren Bindungsstellen zu beschreiben,
ist hinreichend, weiter vorauszusetzen:
- Eine maximale Reaktionsgeschwindigkeit
wird als Rechengröße eingeführt. Diese entspricht dem fiktiven Fall, dass sämtliches vorhandene Enzym als Enzym-Substrat-Komplex vorliegt, also
.
ist zum Anteil
substratgebundenen Enzyms an insgesamt vorhandenem proportional.
Dann hat die Proportionalität die Form
(4)
| Rechnung |
|
Wegen der vorausgesetzten Proportionalität von
Damit ist das Verhältnis von
|
Gleichsetzen mit der Hill-Gleichung ergibt eine Gleichung, die in Abhängigkeit von der
-ten Potenz
der Substratkonzentration darstellt:
(5)
| Rechnung |
|
Gleichsetzen von Gleichung (4) mit der Hill-Gleichung ergibt:
|
Die Herleitung der Gleichung (5) ist der Herleitung der Michaelis-Menten-Gleichung größtenteils analog. Unterschiede sind:
- Die Geschwindigkeitskonstante
der katalysierten Reaktion wird nicht in die Herleitung von Gleichung (5) einbezogen:
hängt im Gegensatz zu
formal nicht von
ab.
- Die Ordnung der katalysierten Reaktion wird bei der Herleitung von (5) nicht explizit betrachtet.
Statt der beiden letztgenannten Voraussetzungen geht die in Gleichung (4) formulierte Proportionalität in die Herleitung ein; ein abstrakter Proportionalitätsfaktor
tritt
an die Stelle von
.
Weitere Darstellung für θ und für v. Die Sättigungsfunktion
In der Hill-Gleichung ist von
und von
abhängig,
selbst aber auch von
(siehe Gleichung (2')). Das Verhalten der Gleichung in Abhängigkeit
von
ist einheitlicher darstellbar (s.u. halblogarithmisch aufgetragene Graphen), wenn
durch
ersetzt wird:
(6)
| Umformung |
|
Einsetzen von (3'):
|
Gleichsetzen der Gleichungen (4) und (6) ergibt eine Darstellung von , die
ebenfalls nicht mehr enthält:
(7)
| Rechnung |
Wenn an ein Molekül Enzym Moleküle Substrat gebunden sind und die Konzentration der
Enzym-Substrat-Komplexe
ist, so ist die Konzentration des gebundenen
Substrats
.
Als Sättigungsfunktion
wird das Verhältnis der Konzentration gebundenen Substrats zur Konzentration
des insgesamt vorhandenen Enzyms bezeichnet:
Der Zusammenhang zur Hill-Gleichung ist wegen gegeben mit
(8)
Der empirische Hill-Koeffizienten nH als Maß der Kooperativität von Enzymen
Gemäß Herleitung der Hill-Gleichung aus dem Massenwirkungsgesetz (s.o.) ist der Hill-Koeffizient die Anzahl der Bindungsstellen eines Enzyms und daher
eine natürliche Zahl. (Genau) für
sind die Konstanten
und
gleich. Auch sind genau für
die Gleichungen (5) und (7) einer Michaelis-Menten-Gleichung äquivalent, indem die Konstante
als Michaelis-Menten-Konstante
aufgefasst wird.
| Rechnung für Gleichung (7) |
|
|
Zu Unterscheidung von wird mit der Variable
derjenige Hill-Koeffizient bezeichnet, für den die Hill-Gleichung die Kinetik eines solchen Enzyms empirisch am besten beschreibt.
ist in der Regel kleiner als
und
keine natürliche Zahl. Die Theorie der Hill-Gleichung ist bei Verwendung von
nur dann mathematisch konsistent, wenn
in allen
zur Beschreibung der Kinetik verwendeten Gleichungen durch
ersetzt wird.
(9)
In Folgenden seien die Konstanten und
in allen zu vergleichenden Situationen der jeweils betrachteten Enzyme gleich.
Der Unterschied zwischen
und
wird
dadurch erklärt, dass Enzyme mit mehreren Substratbindungsstellen aus mehreren Untereinheiten bestehen, die jeweils eine Bindungsstelle tragen und demzufolge
für sich betrachtet mit
und also einer Michaelis-Menten-Gleichung beschrieben werden können.
Ein als positive Kooperativität bezeichnetes
Zusammenwirken der Untereinheiten kann aber auch bewirken, dass ein solches Enzym bei einer vorgegebenen Substratkonzentration
schneller reagiert, als gemäß einer Michaelis-Menten-Gleichung (mit
) zu erwarten wäre. Eine Hill-Gleichung beschreibt
für Konzentrationen
genau dann positive Kooperativität, wenn
ist. Weiter reagiert ein Enzym bei positiver Kooperativität bei einer vorgegebenen Substratkonzentrationen
umso schneller, je größer
ist.
Logische Obergrenze für
ist (die Anzahl der Bindungsstellen)
.
Ganz entsprechend kann ein als negative Kooperativität bezeichnetes Zusammenwirken von Untereinheiten eines Enzyms bewirken, dass jenes bei
einer vorgegebenen Substratkonzentration langsamer reagiert, als gemäß einer Michaelis-Menten-Gleichung
(mit
) zu erwarten wäre. Eine Hill-Gleichung beschreibt für Konzentrationen
genau dann negative Kooperativität, wenn
ist, und bei einer vorgegebenen Substratkonzentrationen
reagiert ein Enzym bei negativer Kooperativität umso langsamer, je kleiner
ist.
| Beweis |
|
Die folgende Ungleichung (i) verwendet Gleichung (7) zur Berechnung der Geschwindigkeiten zweier Enzyme, deren Situationen
sich ausschließlich im Hill-Koeffizienten
der übersichtlicheren Schreibweise dient die Substitution
denn für die Überlegung kann
|
Ein Enzym mit mehreren Bindungsstellen, bei dem ein solches Zusammenwirken der Untereinheiten nicht zu beobachten ist, heißt nicht kooperativ.
Kooperativität ist nicht nur für
Enzyme beschrieben, sondern auch für Nicht-Enzym-Proteine, an die mehrere andere Moleküle binden (s.o. Herleitung der Hill-Gleichung).
Für die koordinative Bindung von Sauerstoff an
Hämoglobin, das aus
je ein Sauerstoffmolekül bindenden Untereinheiten besteht,
wurde ein Hill-Koeffizient
von 2,8 bestimmt.
Berechnung von nH
Sind die Substratkonzentrationen bzw.
bekannt,
bei denen ein Enzym mit 10% bzw. 90% seiner Maximalgeschwindigkeit
reagiert, so lässt sich sein empirischer
Hill-Koeffizient
bestimmen:
Verallgemeinerung: Sind zwei beliebige verschiedene Substratkonzentrationen
bzw.
bekannt, bei denen ein Enzym
mit 0% < P% < 100% bzw. 0% < Q% < 100% seiner Maximalgeschwindigkeit
reagiert, so ist sein empirischer
Hill-Koeffizient
durch den folgenden Quotienten gegeben:
| Herleitung |
|
A. Mit Überlegung (9) ist bei Betrachtung des empirischen Hill-Koeffizienten
B. Mit Gleichung (4): ist
C. (ii) und (iii) ergeben die Proportionalität: Mit einem Logarithmus zu einer wählbaren Basis und der Rechenregel für den Logarithmus einer Potenz:
D. Verallgemeinerung: Für zwei beliebige verschiedene Anteile
wobei der Bruch im letzten Schritt mit |
Nicht linearisierte Graphen
Direkt-lineare Auftragung einer Enzymkinetik nach Michaelis-Menten

Enzymkinetische Parameter lassen sich bequem und präzise direkt aus einer Sättigungshyperbel gemäß der Abbildung herleiten
(„direkt-lineare Auftragung“ auch „Cornish-Bowden-Diagramm“ genannt). In dieser Hyperbel ist die enzymatische Umsatzgeschwindigkeit
(Ordinate) als Funktion
der Substratkonzentration
(Abszisse) dargestellt.
Für die direkt-lineare Auftragung überträgt man die Anfangsgeschwindigkeiten des enzymatischen Umsatzes direkt in das
-
-Diagramm.
Die
-Werte sind vor Versuchsbeginn bekannt
(eingestellte Substratkonzentrationen); während der Versuchsreihe ist dann der Ordinatenwert für
(die Anfangsgeschwindigkeit) nachzutragen.
Aus der maximalen Umsatzgeschwindigkeit
lässt sich die halbe
maximale Umsatzgeschwindigkeit
ableiten.
Graphisch kann man daraus den Koordinatenwert für
ermitteln.
Die katalytische Effizienz
folgt übrigens aus der Steigung der Tangente an den Ursprung:
;
daraus ergibt sich
.
| Berechnung der Steigung der Tangente an den Ursprung |
|
Die Funktionsgleichung der Hyperbel ist die Michaelis-Menten-Gleichung
die Steigung
|
Die Fehlerbehandlung wird im direkt-linearen Plot weitgehend vereinfacht: Mittelwertsbildung gibt dann die wahrscheinlichen Werte
für die Parameter und
. Bei Inspektion der
Streubreite der Messpunkte (nicht identisch mit deren Standardabweichung)
können Ausreißer leicht identifiziert und sogenannte Mediane abgelesen werden.
An dieser Stelle sei erwähnt, dass alle (auch die nachfolgenden) Auswertungsverfahren nicht nur für Enzyme, sondern auch für die Bindungsvorgänge von Carriern oder Rezeptoren Gültigkeit haben. Historisch gesehen wurden all diese Methoden (Hanes und Eadie-Hofstee-Auftragung für Enzyme, Scatchard und Hill-Auftragungen für Carrier) ursprünglich von Woolf entwickelt.
Direkt-linear aufgetragene Graphen einer Enzymkinetik nach Hill für unterschiedliche Werte von nH
Die aus der Hill-Gleichung hergeleitete Gleichung (5) lässt sich als eine Funktion auffassen, die die empirisch gefundene
Reaktionsgeschwindigkeit abhängig von der Substratkonzentration
beschreibt. Nach Überlegung (9) ist bei der
Formulierung der Funktion
durch
zu ersetzen:
f([S]) ist überall streng monoton steigend
und nähert sich für zunehmende der
waagerechten Asymptote
.
Der Graph von f([S]) zeigt aber je nach Wert von
unterschiedliches Verhalten:
- Für
ist er Teil einer Hyperbel, da Gleichung (5) genau dann einer Michaelis-Menten-Gleichung äquivalent ist (s.o.).
- Für
hat er genau einen Wendepunkt bei
. Unter Mitberücksichtigung ihres Steigungsverhaltens ist
daher in diesem Fall eine Sigmoidfunktion. Der Fall
lässt sich von den Fällen
und
durch bloße Betrachtung des Funktionsgraphen unterscheiden.
- Für
hat er keinen Wendepunkt und sieht einem Teil einer Hyperbel ähnlich. Ein solcher Graph heißt pseudohyperbol, weil sich der Fall
vom Fall
durch bloße Betrachtung des Graphen nicht unterscheiden lässt.
| Rechnerische Nachweise |
|
Vorüberlegungen:
A. Für beliebige
B. Die Ableitung ist mit (i) und (iii) überall positiv für C. Die Wendepunkte von
Da
Mit (ii) hat Gleichung (iv) genau dann eine Lösung, wenn Mit Mit von Gleichung (iv) existiert; Für beliebige
Für eine geeignete Mit die entsprechenden Umformungen, dass Letzteres zeigt zusammen mit (v) den Vorzeichenwechsel von |
Halblogarithmisch aufgetragene Graphen einer Hill-Gleichung für unterschiedliche Werte von nH
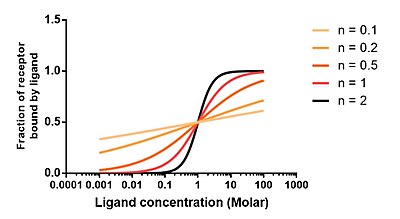
Im nebenstehenden Diagramm ist die Ordinate
der Anteil substratgebundenen Enzyms an insgesamt vorhandenem.
Die Abszisse gibt das Verhältnis
an;
sie ist logarithmisch geteilt. Bei Verwendung des dekadischen Logarithmus ist
- wegen
der Punkt „1“ Nullpunkt der Abszisse und
- wegen
und
der Abstand zwischen den Punkten „1“ und „10“ Längeneinheit der Abszisse.
Für beliebiges bezeichnet ein
Längeneinheiten vom Nullpunkt entfernter
Punkt der Abszisse die Substratkonzentration
,
wobei der Faktor
auf der Abszisse ablesbar ist.
Jeder Graph des Diagramms zeigt eine Hill-Gleichung der Form (6):
.
| Erläuterung |
|
Jeder Graph des Diagramms zeigt eine Funktion
wie durch Betrachtung des Verhaltens dieser Funktion für
zeigt, dass jeder Graph auch eine Hill-Gleichung der Form (6) darstellt:
|
Für je einen vorgegebene Hill-Koeffizienten
ist im Diagramm der Graph der
Hill-Gleichungen zu allen Werten von
gleich, da
nicht direkt von
abhängt,
sondern vom Verhältnis
.
Die Gesamtheit der Graphen bildet für beliebige positive
eine (einparametrige)
Schar direkt vergleichbarer Kurven; Teile einer Hyperbel oder
pseudohyperbole Kurvenverläufe treten nicht auf.
Jeder Graph des Diagramms ist auch Graph einer
logistischen Funktion
und hat daher
- für
die Asymptote
sowie
- für
die Asymptote
;
- jeder Graph ist punktsymmetrisch mit Symmetriezentrum
;
ist der Wendepunkt jeder Funktion
;
- die Steigung von
in
ist
. In diesem Sinne nimmt die Steilheit des Graphen mit
zu.
| Beweis |
|
Die allgemeine logistische Funktion
mit
Die Eigenschaften der allgemeinen logistischen Funktion setzen sich auf
|
Weiter gehört jede logistische Funktion zu den Sigmoidfunktionen, d.h. jeder ihrer Graphen verläuft S-förmig.
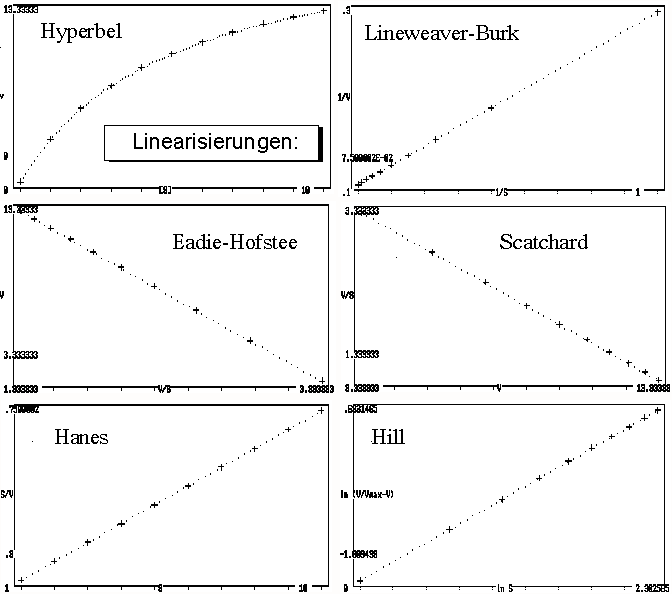
Linearisierungsverfahren
Linearisierungsverfahren wurden in der Vergangenheit sehr häufig für die schnelle grafische Bestimmung der wichtigen
Kinetikparameter und
verwendet.
Sie sind zwar einprägsam und verbreitet, führen jedoch zu einer teils erheblichen Verfälschung des Ergebnisses durch Messfehler
und sind zur Fehlerbetrachtung mehr oder weniger ungeeignet. Mittlerweile hat die Ermittlung der Michaelis-Menten-Parameter
durch nichtlineare Regression stark an Bedeutung gewonnen, die zu deutlich genaueren Ergebnissen führt.
Deshalb sollen die Linearisierungsverfahren hier nur gestreift werden.
Lineweaver-Burk-Diagramm
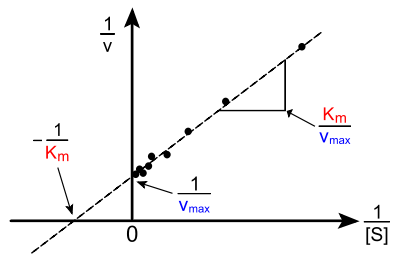
Hans Lineweaver (1907–2009) und
Dean Burk (1904–1988) haben 1934 eine doppelt-reziproke
Darstellung vorgestellt, bei der
als Funktion von
aufgetragen wird.
Eine Umformung der Michaelis-Menten-Gleichung ergibt die folgende Gleichung:
| Umformung |
|
|
Die Steigung dieser linearen Funktion beträgt
;
sie schneidet
- die
-Achse bei
(Ordinatenabschnitt) und
- die
-Achse bei
(Abszissenabschnitt).
| Rechnung zu Achsenabschnitten und Steigung |
|
Indem eine lineare Funktion. Für diese lassen sich
Steigung
Sei
Dann ist das Dreieck
|
Obwohl sie zur Datenrepräsentation meist verwendet wird, ist diese Methode zur Auswertung jedoch unverlässlich. Kleine Fehler in
ergeben bei kleinen
-Werten eine große Abweichung in
, bei großen
-Werten ist diese eher zu vernachlässigen.
Die Autoren der Methode haben die Unsicherheit großer
Werte betont und darauf hingewiesen, dass diese grundsätzlich geringer zu gewichten sind. Spätere Anwender haben dies
zumeist ignoriert. Wo immer möglich sollte dieses durch Computerverfahren zur Bestimmung enzymkinetischer Parameter ersetzt werden.
Eadie-Hofstee-Diagramm
Das Eadie-Hofstee-Diagramm, auch Woolf–Eadie–Augustinsson–Hofstee- oder Eadie–Augustinsson-Diagramm, nimmt eine Mittelstellung ein.
Hierbei wird als Funktion von
aufgefasst.
Die zugehörige Umformung der Michaelis-Menten-Gleichung ergibt:
| Umformung |
|
Umformung der linken Seite:
|
Aus dem Diagramm lässt sich auf der -Achse als
Ordinatenabschnitt
ablesen, aus der (negativen)
Steigung
der Regressionsgeraden
bestimmen.
Der Fehler wächst mit v/[S]. Da v bei beiden Koordinaten eingeht, konvergieren alle Abweichungen zum Ursprung.
Scatchard-Diagramm
Das Scatchard-Diagramm fasst umgekehrt
als Funktion von
auf. Es entsteht aus dem Eadie-Hofstee-Diagramm durch
Vertauschung der Achsen (oder äquivalent: durch Spiegelung des Diagramms insgesamt an der
1. Winkelhalbierenden des Koordinatensystems).
Die entsprechende Umformung der zum Eadie-Hofstee-Diagramm gehörigen Gleichung ergibt:
| Umformung |
|
|
Aus dem Diagramm lässt sich ebenfalls auf der -Achse, die nun
Abszisse ist,
als
Abszissenabschnitt ablesen, denn ein Ordinatenabschnitt des
Eadie-Hofstee-Diagramms geht durch die genannte Spiegelung in einen Abszissenabschnitt des Scatchard-Diagramms über.
Ebenso lässt sich aus der (negativen) Steigung
der Regressionsgeraden durch Übergang zur reziproken Zahl und Vorzeichenwechsel
bestimmen. Der
Ordinatenabschnitt der Gerade im Scatchard-Diagramm
ist der im Abschnitt "Direkt-lineare Auftragung" als Maß der katalytischen Effizienz genannte Bruch.
Das Scatchard-Diagramm wird
zumeist zur Repräsentation von Bindungsmessungen (anstelle enzymkinetischer Daten) angewendet. Scatchard- und Eadie-Hofstee-Diagramme
gelten als die besten Werkzeuge zur Diagnose
kooperativer Phänomene. Im Falle
negativer Kooperativität oder nicht-identischer, isolierter Bindungsplätze entsteht ein konkaver Verlauf mit linearem Endast.
Die Steigungen entsprechen hier den Affinitäten (Kd beziehungsweise
) und die Gesamtzahl der Bindungsplätze (aktiven Zentren)
ist aus dem Schnittpunkt mit der
-Achse abzulesen.
Hanes-Woolf-Diagramm (Hanes(-Wilkinson)-Diagramm)
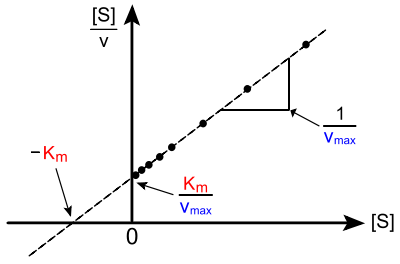
Das Hanes-Woolf-Diagramm ist die bestmögliche lineare Auftragungsmöglichkeit. Es geht auf Charles Samuel Hanes (1903–1990) und Barnet Woolf (1902–1983) zurück. Hierbei wird eine Umformung der Michaelis-Menten-Gleichung verwendet, die [S]/v als Funktion von [S] darstellt:
| Umformung |
|
|
Die Steigung dieser linearen Funktion beträgt
;
sie schneidet
- die
-Achse bei
(Ordinatenabschnitt) und
- die
-Achse bei
(Abszissenabschnitt).
| Rechnung zu Achsenabschnitten und Steigung |
|
Für die lineare Funktion mit der Gleichung lassen sich Steigung
Sei
Dann ist das Dreieck
|
Fehler in [S]/v sind eine weit bessere Annäherung der Fehler in v. Aufgrund einer unverfälschten Spreizung der Messpunkte entlang der [S]-Achse wird das Ergebnis durch einzelne Ausreißer prinzipiell weniger verfälscht. Da aber abhängige und unabhängige Variable vermischt werden, ist auch hier eine Datenoptimierung durch lineare Regression nicht sinnvoll.
Hill-Diagramm
Das Hill-Diagramm ist eine Darstellung der Hill-Gleichung, in der
(Ordinatenwert) als Funktion von
(Abszissenwert) aufgetragen wird.
Die zugehörige Umformung der Hill-Gleichung ergibt:
(10)
| Umformung |
|
Die Hill-Gleichung wird nach Ersetzen vom
mit der Rechenregel für den Logarithmus eines Quotienten bzw. den Logarithmus einer Potenz:
|
Bei Verwendung von hat (10) die Form:
(10a)
| Umformung |
|
Die Definition der Halbsättigungskontante
mit der Rechenregel für den Logarithmus einer Potenz: dies kann in (10) eingesetzt werden. |
Auch in den hier folgenden Gleichungen kann an die Stelle von
treten.
Ist bekannt, so lassen sich die
Ordinatenwerte unter Verwendung von
bestimmen:
(10b)
| Umformung |
|
Die Gleichungen (10) und (10b) sind äquivalent, wenn das Argument des Logarithmus der linken Seite für beide Gleichungen übereinstimmt.
Einsetzen von Gleichung (4) und Erweitern mit
|
Die Sättigungsfunktion kann in die Gleichung eingeführt werden:
(10c)
| Umformung |
|
Die Definition der Sättigungsfunktion
die Gleichungen (10) und (10c) sind äquivalent, wenn das Argument des Logarithmus der linken Seite für beide Gleichungen übereinstimmt.
Erweitern mit |
Insoweit die Hill-Gleichung eine Enzymkinetik zutreffend beschreibt, zeigt das Hill-Diagramm eine Gerade
, aus der sich
als deren Steigung und
als Abszissenabschnitt (= Abszissenwert des Schnitts von
mit der Abszisse)
ablesen lässt; hieraus lässt sich nach Delogarithmieren und nach Berechnung von
und anschließendem Delogarithmieren auch
bestimmen.
| Begründung und Rechenhinweise |
|
A. Diejenigen Varianten der Gleichung (10), die den Summanden
und sind daher als Funktionsvorschrift einer
linearen Funktion mit Steigung
B. Zur Bestimmung des Abszissenabschnitts
wie im Text angegeben. Bemerkung: Diejenigen Varianten der Gleichung (10), die den Summanden
Aus mathematischer Sicht könnte zur hier beschriebenen Rechnung eine beliebige Basis verwendet werden, üblich sind jedoch vor allem
jeweils entsprechend zum Delogarithmieren von Im angelsächsischen Sprachraum wird nicht nur der allgemeine, sondern auch der natürliche Logarithmus zuweilen mit
|
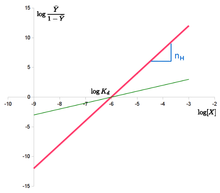
Im nebenstehenden Hill-Diagrammen ist die Abszissenvariable mit
bezeichnet,
der Abszissenabschnitt
mit
,
die Ordinatenvariable
mit
.
(Die Längeneinheit ist für beide Achsen unterschiedlich gewählt, sodass die Steigung der roten Gerade nicht
ist.
Der Schnitt einer Gerade mit der eingezeichneten Ordinate, die nicht durch den Nullpunkt der Abszisse führt,
ist nicht der Ordinatenabschnitt der jeweiligen Gerade.)
Für den gleichen Abszissenabschnitt
(und damit den für beide Geraden gleichen Wert von
) ist
- die rote Gerade das Hill-Diagramm eines hochkooperativen Enzyms (Schnitt mit der Ordinate bei
Geradensteigung
);
- die grüne Gerade dasjenige eines kaum oder nicht kooperativen Enzyms (Schnitt mit der Ordinate bei
Geradensteigung
).
Wenn die berechneten Wertepaare nicht auf einer Gerade liegen, kann diese außer durch zufällige auch durch systematische Fehler bedingt sein, denn die Hill-Gleichung setzt voraus, dass der Hill-Koeffizient für alle Konzentrationen gleich ist. Eine Abweichung hiervon fand G.S. Adair, der ebenfalls die Sauerstoffbindung von Hämoglobin untersuchte.
Zusammenstellung von Linearisierungen einer Hyperbel
Inhibitoren
Hauptartikel: Enzymhemmung
Viele Therapeutika und Gifte sind Hemmstoffe (Inhibitoren) von Enzymen. Aus diesem Grunde ist der Aufklärung des Wirkungsmechanismus immer eine besondere Bedeutung zugekommen. Die Nomenklatur der Hemmtypen wurde von William Wallace Cleland (* 1930) 1963 auf eine systematische Grundlage gestellt, leider werden in vielen Lehrbüchern immer noch Begriffe abweichend verwendet.
Hier sollte allerdings beachtet werden, dass sich klassische Analysen auf reversibel bindende Stoffe beschränken. Irreversible Bindung einer Substanz an ein Enzym führt zur Inaktivierung, nicht zur Hemmung.
Abgeleitet aus der Michaelis-Menten-Gleichung
stellt sich die allgemeine
Inhibitionsgleichung wie folgt dar:
Danach kann das Verhältnis des -Wertes
(Dissoziationskonstante des Komplexes EI) und des
-Wertes
(Dissoziationskonstante des Komplexes EIS) zur Ableitung des Inhibitionstyps dienen:
Kompetitiv
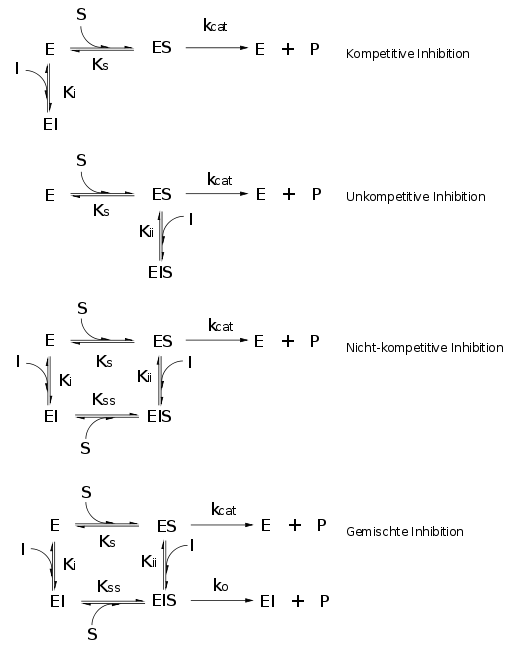
Inhibitor und Substrat schließen sich gegenseitig von der Bindung an das Enzym aus. Dies bedeutet jedoch nicht notwendigerweise, dass der Inhibitor an der gleichen Bindungsstelle bindet wie das Substrat. Auch wenn die Bindung von Substrat bzw. Inhibitor zu Konformationsänderung im Enzym führen, welche die Bindungsstelle für den jeweils anderen blockieren, ist die Hemmung kompetitiv. Wenn Substrat und Inhibitor allerdings die gleiche Bindungsstelle haben, dann ist der Hemmtyp notwendig kompetitiv.
Bei der Kompetitiven Hemmung kann der Inhibitor durch Substrat aus dem Enzym verdrängt werden,
ändert sich also nicht.
Allerdings wird für jede gewünschte Geschwindigkeit eine höhere
benötigt, die scheinbare
wird also mit steigender
höher.
Im Lineweaver-Burk-Diagramm führt dies bei unterschiedlichen
beziehungsweise
zu einer Schar von Geraden,
die einen gemeinsamen Schnittpunkt auf der y-Achse bei (
) haben.
Unkompetitiv
Der Inhibitor bindet nicht an das freie Enzym, sondern an den ES-Komplex. Höhere Konzentrationen des Substrates können daher den
Hemmstoff nicht vom Enzym verdrängen, sondern führen zu vermehrter Bindung. Umgekehrt vermindert Bindung des Hemmstoffes
die Konzentration von ES, nach dem Prinzip von Le Chatelier muss sich also zusätzliches ES aus E und S bilden:
Die scheinbare vermindert sich,
die Affinität des Enzymes für das Substrat steigt mit steigender
. Gleichzeitig nimmt natürlich
ab.
Im Lineweaver-Burk-Diagramm finden wir eine Schar paralleler Geraden.
Nicht-kompetitiv
Der Inhibitor kann sowohl an E als auch an ES binden. Im einfachsten Fall ist dabei
, d.h.,
dass die Substratbindung die Affinität des Enzymes für den Inhibitor nicht verändert, etwa durch Konformationsänderung.
Dann folgt natürlich auch, dass die Bindung des Inhibitors die Affinität des Enzymes für das Substrat nicht ändert
und
. Wegen des Zusammenhangs zwischen
und
ändert die Bindung von Inhibitor also auch nicht
.
Es lässt sich nun zeigen (durch Substitution und Eliminierung aus den Definitionen von
und
), dass
.
Wenn also
, dann folgt
und die scheinbare
steigt mit
.
Falls andererseits
,
dann folgt
und die scheinbare
sinkt mit steigendem
.
Die nicht-kompetitive Hemmung führt im Lineweaver-Burk-Diagramm zu einer Schar von Geraden mit gemeinsamen
Schnittpunkt links von der y-Achse, der Schnittpunkt liegt auf der x-Achse wenn
, er liegt über der x-Achse falls
und unter der x-Achse falls
.
Gemischt-kompetitive Hemmung
Der Mechanismus dieses Hemmtyps (der in der Praxis von geringer Bedeutung ist) ähnelt der nicht-kompetitiven Hemmung,
allerdings hat der EIS-Komplex noch eine katalytische Aktivität. Auch das Lineweaver-Burk-Diagramm sieht aus wie bei der
nicht-kompetitiven Hemmung (mit allen 3 Möglichkeiten). Im sog. Sekundärdiagramm (Steigung bzw. y-Schnittpunkt im
Lineweaver-Burk-Diagram als Funktion von ) sieht man aber im
Falle der nicht-kompetitiven Hemmung Geraden, im Falle der gemischt-kompetitiven jedoch Kurven.
Siehe auch
- Allosterie
- exergon
- Fließgleichgewicht
- Mehrsubstratreaktion
- Pasteur-Effekt
- Substratzyklus
- Wechselzahl
Literatur
- H. Bisswanger: Enzymkinetik – Theorie und Methoden. 3. Auflage. Wiley-VCH, Weinheim 2000, ISBN 978-3-527-30096-9.
- E. Buxbaum: Fundamentals of protein structure and function. Springer, New York 2007, ISBN 978-0-387-26352-6.
- G. E. Briggs, J. B. Haldane: A Note on the Kinetics of Enzyme Action. In: Biochemical Journal. Band 19, Nr. 2, 1925,
S. 338–229;
 PMID 16743508.
PMID 16743508. - L. Michaelis, M. L. Menten: Die Kinetik der Invertin-Wirkung. In: Biochemische Zeitschrift. Band 49, 1913, S. 333–369.
- I. H. Segel: Enzyme Kinetics. Wiley, New York 1975 (Nachdruck 1993).
- S. P. L. Sørensen: Enzymstudien II. Über die Messung und Bedeutung der Wasserstoffionenkonzentration bei enzymatischen Prozessen. In: Biochemische Zeitschrift. Band 21, 1909, S. 131–304.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 28.06. 2024